Matlab多元线性回归预测城市建成区面积
2018-06-29曹应举张永彬温继满刘佳丽
曹应举,张永彬,温继满,汲 姣,刘佳丽
(1.华北理工大学 矿业工程学院,河北 唐山 063210;2.开滦安全技术培训中心,河北 唐山 063000)
0 引言
随着经济的发展,城市化速度加快,城市的面积在不断的扩张。为了了解城市的扩张动态,获取城市扩张的历史轨迹,许多学者对城市建成区面积的预测问题进行了研究:李爱民利用遥感技术对不同年份城市建成区多期遥感影像进行提取分类,分析了城市扩张的时空规律[1];刘柯运用BP神经网络方法建立预测模型,使用多期数据作为学习样本和检验样本,对2005年北京市城市建成区面积进行了模拟预测[2];雷波通过建立多元回归模型,选用13个社会和经济驱动因子,对福州城市建成区面积的扩张驱动进行了回归分析[3]。在模拟预测方面,多元回归模型是一种常用的预测模型,其预测精度高、应用领域广泛,例如,周永生等通过综合影响粮食产量的多种因素,将多元回归分析应用于粮食产量的预测中[4];付倩娆通过对不同大气成分浓度数据进行分析,将多元回归分析应用在雾霾的预测中[5];叶锋通过综合考虑经济技术等多种影响因子,将多元回归分析应用于油田产量的预测中[6];韦浩采用不同方法对滑坡距离进行预测,得出结论是“与传统预测方法相比,多元回归分析法所建立的预测模型精度较高”[7]。但传统的用纯数学方法来实现多元线性回归方程求解的过程比较繁琐,为了简化计算难度,提高计算的速度,本文以Matlab为语言平台、以回归分析为数学统计方法,建立关于建成区面积与其影响因子的多元回归模型,并应用其进行城市建成区面积的预测。
1 线性回归模型
变量Y的值主要受影响因子X(由X1,X2,…,Xk确定,可以表示为X1,X2,…,Xk的某个函数关系式:Y=f(X1,X2,…,Xk))和随机误差ε的影响,本研究将自变量写成如下形式:
Y=f(X1,X2,…,Xk)ε。
(1)
其中,随机变量Y称为被解释变量或因变量;X1,X2,…,Xk称为解释变量或自变量。f(X1,X2,…,Xk)为一般变量X1,X2,…,Xk的确定性关系,ε为随机误差。
当概率模型式(1)中回归函数为线性函数时,即有
Y=β0+β2X1+…βkXk+ε。
(2)
其中β0,β1,β2,…,βk是k+1个未知参数,β0称为回归常数,β1,β2,…,βk称为回归系数,Y称为被解释变量(因变量),而X1,X2,…,Xk是k个可以控制的一般变量,称为解释变量(自变量)。k=1时,为一元线性回归模型;k≥2时,称为多元线性回归模型。
线性回归模型的“线性”是针对未知参数βi(i=0,1,2,…,k)而言的。对于回归解释变量的线性是非本质的,因为解释变量是非线性的,常可以通过变量的替换把它转化成线性的。
若(Xi1,Xi2,…,Xik;Yi),i=1,2,…,n是式(2)中变量(X1,X2,…,Xk;Y)的一组观测值,则线性回归模型可表示为
Yi=β0+β1Xi1+…βkXik+εi。
(3)
其中E(Yi)=β0+β1Xi1+…βkXik为多元回归方程组,其相应的矩阵表达式为
Y=xβ。
(4)
其中回归系数的最小二乘估计为
(5)
2 建成区面积案例分析
通过搜集《中国统计年鉴》(2016)和地方统计年鉴整理获得25个省会城市2015年的建成区面积。鉴于影响建成区面积有诸多因素,本文在参照已有研究成果的基础上,结合实际情况,构建了城市建成区面积的经济社会影响因子体系(如图1所示),并通过建立多元回归模型进行分析和检验,从而对未来的城市建成区面积进行预测。
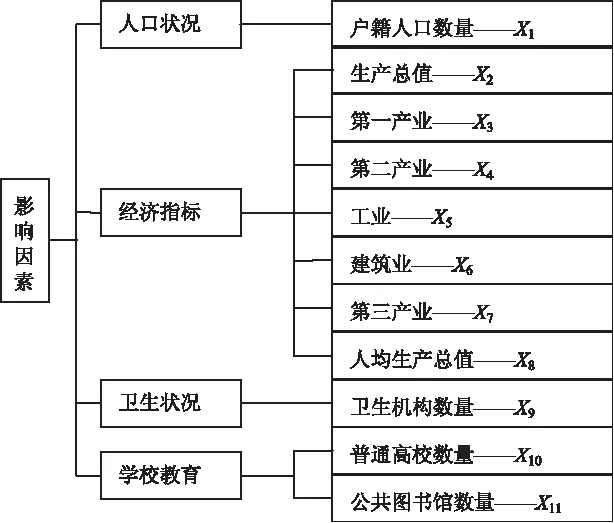
图1 建成区面积影响因子
3 数据处理
Matlab多元线性回归数据处理过程包括数据预处理、建模、分析及预测四大部分,其具体步骤如图2所示。

图2 线性回归流程图
3.1 利用regress函数实现多元线性回归
在Matlab中使用命令regress实现多元线性回归,调用格式为:b=regress(Y,X),[b,bint,r,rint,stats]=regress(Y,X,alpha)[8],其中:Y表示一个n-1的因变量数据矩阵;X是n-p矩阵,自变量X是一列具有相同行数,值是1的矩阵的组合;alpha为显著性水平(缺省时设定为0.05);输出向量b为回归系数最小二乘估计值;bint为b的置信区间;r,rint为残差及其置信区间。
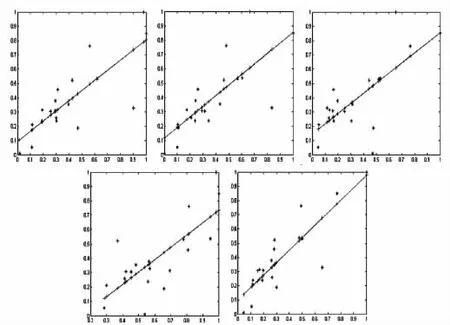
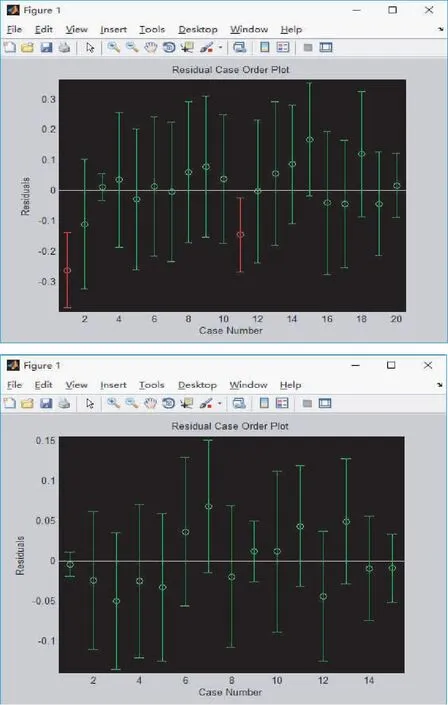
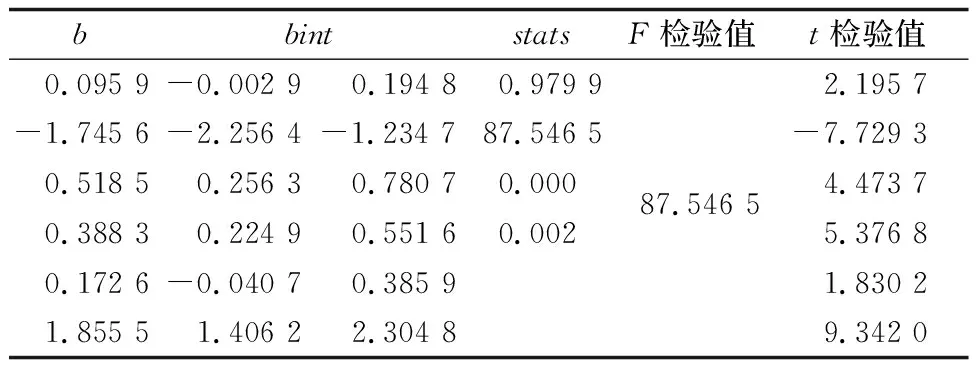
stats是用于检验回归模型的统计量,第一个是R2,其中R是相关系数;第二个是F统计量值;第三个是与统计量F对应的概率P;第四个是S2,为误差方差估计值。R2越接近1,说明回归方程越显著;F>F1-alpha(P,n-p-1)时拒绝H0,F越大,回归方程越显著;与F对应的概率P 为了方便数据处理,需要对样本中的各影响因子进行归一化处理。归一化是一种消除指标之间量纲影响的简化计算方法,常用的数据归一化方法有“最小-最大标准化”“Z-score标准化”和“按小数定标标准化”等,本文采用的是“最小-最大标准化”方法对原数据进行线性变换。将A中的一个原始值X通过“最小-最大标准化”映射成在区间[0,1]中的值X′,其形式如式(6)所示。 (6) 其中:X′为归一化后的数据,X为原始数据,Xmin和Xmax分别是X的最小值和最大值。 通常认为数据矩阵X是给定的,不存在误差,但是如果数据矩阵X也存在误差或者扰动,那么最小二乘估计从统计观点看就不再是最优的,它将是有偏的,而且偏差的协方差将由于X的噪声误差的作用而增加。因此,当X也存在误差时,应该使用整体最小二乘进行回归[9]。 (7) 或 (8) (9) 或等价为 (B+D)Z=0。 (10) ‖D‖F=min。 (11) 其中‖D‖F是D的F(Frobenius)范数。 若想使得所拟直线有实际意义,必须保证建成区面积(变量Y)与其影响因子(自变量X)存在线性相关性[10],描述它们之间相关性系数的定义为: (12) 其估值为: (13) 当ρ越接近±1时,表明随机变量Y与X的相关性越密切,即所建立的线性模型和实际的试验情况越接近。 在Matlab中使用corrcoef函数可以求两个序列的相关度,corrcoef(X,Y)表示序列X和序列Y的相关系数,得到的结果是一个2*2矩阵。 相关系数的大小所表示的意义通常如表1所示。 表1 相关系数表示的意义 依据相关系数表,编写相应程序代码,将相关程度在微相关范围内的影响因子(户籍人口数量X1,第一产业X3,人均生产总值X8,卫生机构数量X9,普通高校数量X10,公共图书馆数量X11)予以剔除,保留相关系数大于0.3的影响因子,剩余5个影响因子(生产总值X2,第二产业X4,工业X5,建筑业X6,第三产业X7)的相关程度显著,对因变量建成区面积Y的解释程度较高。 创建城市建成区面积Y和5个影响因子(生产总值X2,第二产业X4,工业X5,建筑业X6,第三产业X7)的一元线性回归预测方程,如表2所示。 表2 一元线性回归预测方程 根据表2的拟合方程结果来看,建成区面积Y与各个影响因子X的拟合效果良好。对于R2来说数值越大拟合效果越好,各个方程的判定系数最低为0.527,总体来说判定系数比较高,所以建成区面积与各个影响因子拟合效果总体较好。为了进一步探讨建成区面积与各个影响因子之间的关系,以建成区面积Y为因变量,以影响因子X2-X7为自变量进行多元线性回归分析。 绘制因变量Y与自变量X2-X7之间的散点图,如图3所示。 图3 Y与X2,X4,X5,X6,X7的散点图 模型建立过程中绘制的残差图会有异常点而影响模型的正确性,需要对异常点进行剔除,利用Matlab编写简单的循环语句可以实现以上操作,剔除完成后绘制残差图如图4所示。 图4 异常点剔除前后的残差图 剔除残差后利用regress再次求解参数,结果如表3所示。 表3 参数求解 t检验是逐一对参数的显著性进行检验。其原理是|t(f)|>tα/2时,接受H0,查表可得,tα/2=2.262,经检验,t检验统计量小于tα/2的常数项以及自变量X6显著性不明显,应予以剔除。stats中第1个参数R2是回归平方和与总离差平方和的比值,其值越大越好,该模型达到0.979 9;第2个参数f统计量,越大越好,本模型为87.546 5;第3个参数为P的显著性概率,应该小于0.05,越接近0越好,本模型基本为0;第4个参数为估计误差方差,本模型估计误差方差为0.002,综上,stats中4个参数充分说明回归方程显著,该回归模型成立。 因此,最终建立的多元线性回归方程式为: Y=1.746X2+0.519X4+0.388X5+1.856X7。 对城市建成区面积进行回归分析的目的主要是进行预测和控制[11]。未来城市建成区的面积通过单一的往年建成区增减面积来预测难以定性和定量,所以在实际生活中,都是通过近几年的数据构建主要影响因子和建成区面积的方程,通过观测影响因子,来预测未来的城市建成区面积。 Matlab自带程序rstool可以实现回归分析的控制预测功能,在本例中选择5个城市的建成区面积留做预测,选出未参与回归处理的5组数据,将其自变量影响因子X输入相应位置,Matlab将自动计算预测结果,如图5所示。 图5 rstool预测处理 将Matlab计算结果与经过归一化后的真实值进行比对,预测值在限差范围内,说明了回归方程的正确性,结果比对如表4所示。 表4 实际值与预测值比对 结果显示,第一、三、四、五组数据的实际值都在预测区间内,预测的可靠性高,第二组数据预测结果不理想,导致该结果的原因可能是由于各种因素之间产生了更为复杂的相互作用,使得城市建成区面积不再表现为线性关系中那种按比例的规则变化,而代之以不按比例、不规则的变化或突变。例如,城市区划调整使城市建成区面积和城市经济社会指标突然变化,这必然使传统的基于线性假设的回归预测模型产生很大的误差。 城市建成区面积是人口、经济、社会、环境等多因素综合影响的结果,从本研究中发现,2015年所选25个省会城市的建成区面积受第三产业和国民生产总值的影响最大,第二产业和工业的影响次之。说明要想对城市进行合理建设使之健康发展,应该以大力调控第三产业、国民生产总值为出发点。 本文利用建成区面积作为研究变量,运用Matlab软件建立多元线性回归模型,利用最小二乘原理求解数学模型中的最优解,不仅简化和优化了繁琐的计算过程,而且通过检验证明所建立的模型计算结果精度较高,对城市建成区面积变化的预测有一定的参考价值。然而,由于在实际情况中城市建成区面积受复杂的多种因素影响,在建模过程中对因素考虑或选择不同,则会造成计算结果的多样性,因此,在研究中应力求完善。 参考文献: [1] 李爱民.基于遥感影像的城市建成区扩张与用地规模研究[D].郑州:解放军信息工程大学,2009. [2] 刘柯.基于主成分分析的BP神经网络在城市建成区面积预测中的应用——以北京市为例[J].地理科学进展,2007(6):129-137. [3] 雷波.BP神经网络和多元回归模型在城市建成区面积预测中的应用比较——以福州市为例[J].城市发展研究,2008(1):153-155. [4] 周永生,肖玉欢,黄润生.基于多元线性回归的广西粮食产量预测[J].南方农业学报,2011,42(9):1165-1167. [5] 付倩娆.基于多元线性回归的雾霾预测方法研究[J].计算机科学,2016,43(S1):526-528. [6] 叶锋.多元线性回归在经济技术产量预测中的应用[J].中外能源,2015,20(2):45-48. [7] 韦浩.多元回归分析法在滑坡空间预测中的应用[D].西安:长安大学,2011. [8] 张智星.MATLAB程序设计与应用[M].北京:清华大学出版社,1993:56-65. [9] 邱卫宁,陶本藻.测量数据处理理论与方法[M].武汉:武汉大学出版社,2008:109-113. [10] 刘大杰,陶本藻.实用测量数据处理方法[M].北京:测绘出版社,2000:7-14. [11] 王乐洋,朱建军.回归分析、测量平差与大地测量反演[J].测绘通报,2007(2):27-30.3.2 原始数据归一化
3.3 整体最小二乘(TLS)多元回归
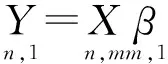
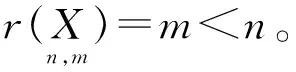
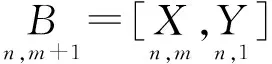
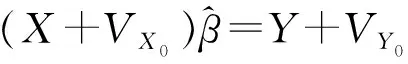
3.4 相关性检验


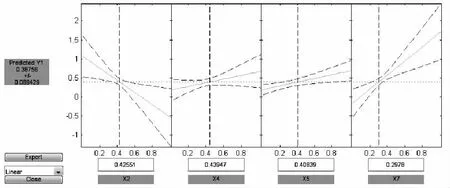
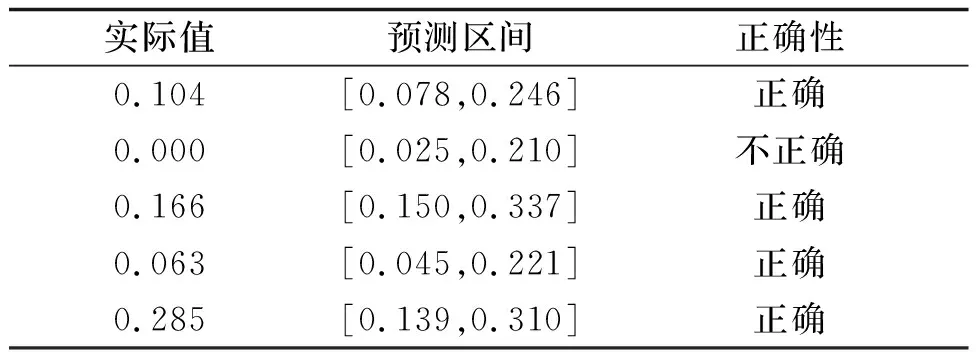
3.5 结果预测
4 小结
