一种基于盐水模型的聚合物驱高效模拟新方法
2018-06-28未志杰
未志杰
(1.海洋石油高效开发国家重点实验室,北京100028;2. 中海油研究总院有限责任公司,北京 100028)
聚合物驱是提高原油采收率的有效方法[1-3],为实现聚合物驱开发效果的定量模拟,石油公司与研究机构开发出多款聚合物驱数值模拟软件,按照相间物质平衡处理方式可分为黑油与组分两种类型,前者包括Eclipse、VIP-Polymer等;后者包括STARS、UTCHEM、INTERSECT等。
现有黑油类型聚合物驱模拟器受限于线性求解算法方面的不足,计算效率难以适应网格规模超过百万节点的大规模复杂油藏模拟,如笔者所研究的某大型河流相稠油油田,存在多个油水系统与多条断层,地质模型约500万网格,完成单次虚拟开发模拟耗时21.4 d(最大时间步长30 d)。而组分类型模拟器,特别是基于状态方程(EOS)的组分模拟器,相比黑油类模型还需要耗费额外计算资源用于确定各组分的相间物质交换情况,大幅拉低了计算效率。研究表明,组分模拟75%的计算耗时用于闪蒸运算[4-5]。聚合物驱模拟器计算效率的不足,严重影响了复杂油藏开发决策速度,亟待建立高效模拟新方法。
调研发现,盐水模型根据典型黑油模型经过简单改造而来,其数值离散得到的Jocobian矩阵性质与黑油模型相似,且两者非线性程度相当,目前已存在众多针对盐水模型的高速求解算法与模拟软件[5-7]。鉴于此,笔者尝试建立一种基于盐水模型的聚合物驱高效模拟新方法,可显著提升聚合物驱模拟速度,同时能够合理、全面地考虑聚合物驱提高采收率关键机理。目前相关方面的研究较少。
本文首先构建基于盐水模型的聚合物驱高效模拟新方法;进而分别从与传统聚合物驱模拟结果对比、不可及孔隙体积影响显著性、吸附滞留损失影响显著性三方面论证了模拟新方法的准确性与适用性;最后应用该方法对具有近500万网格规模的某大型稠油油田开展聚合物驱模拟,以检验其高效性与应用价值。
1 模拟新方法的构建
首先分别阐述聚合物驱数学模型与盐水数学模型,而后对两者进行对比分析,并在此基础上构建基于盐水模型的聚合物驱高效模拟新方法。
1.1 传统聚合物驱数学模型
聚合物驱油机理是通过增加驱替相黏度、降低驱替相有效渗透率,从而改善地层油水流度比,达到扩大波及体积进而提高采收率的目的[8]。聚合物在多孔介质运移过程中,聚合物与岩石及地层流体相互作用,产生复杂的物理化学现象,包括聚合物在岩石表面的吸附、喉道处滞留捕集、不可波及孔隙体积、增黏作用以及残余阻力等[9]。综合考虑上述驱油机理和物理化学现象,研究者建立了多种聚合物驱模型,其中传统数学模型表达式见方程(1)。
油组分:
气组分:
水组分:
聚合物:
(1)
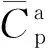
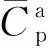
(2)
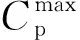
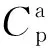
(3)
式中,a、b为聚合物吸附常数。
聚合物注入地层后,驱替相黏度显著增加,且其黏度μeff是聚合物溶液浓度的函数,见方程(4)。
μeff=f(Cp)(4)
1.2 盐水数学模型
地层水中溶解的盐分等矿物质有时能够明显影响水相PVT属性,由此发展出盐水模型,其控制方程如式(5)所示。
油组分:
气组分:
水组分:
盐组分:
(5)
盐水模型相对简单,除需修正水相PVT属性外,并无其他复杂的物理化学现象需要刻画,地层水黏度μeff是盐分浓度Cs的函数,见方程(6)。
μeff=f(Cs)
(6)
1.3 基于盐水模型的聚合物驱高效模拟新方法
对比传统聚合物驱模型(方程(1))与盐水模型(方程(5)),两者油组分与气组分连续方程相同,仅在水组分、聚合物组分方程存在区别,包括如下三方面。
(1) 水相流度表征不同,见水组分、聚合物/盐组分方程左端流动项。
聚合物可显著增加驱替相黏度,降低驱替相渗透率,从而有效改善流度比,事实上这也是聚合物驱提高采收率的核心机理。聚合物驱条件下水相流度见方程(7)。
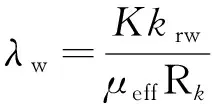
而盐水模型中NaCl等电解质不改变渗透率,仅改变黏度,其流度表达式见方程(8)。
(8)
(2) 是否考虑不可及孔隙体积IPV,见聚合物组分方程右端累计项1。
聚合物直径较大,存在难以波及的小孔隙,即不可及孔隙体积数IPV>0;而NaCl等电解质离子很小,不存在不可及孔隙体积。
(3) 是否考虑吸附损失,见聚合物组分方程右端累计项2。
聚合物分子吸附于岩石表面,产生吸附滞留损失,而盐水模型一般不考虑该损失。
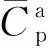
(9)
联立方程(2)与方程(9),可建立残阻系数Rk与聚合物溶液浓度Cp的关系,见方程(10)。
(10)
结合聚合物溶液黏度μeff表达式方程(4),可知聚合物驱流度分母项μeffRk仅为聚合物溶液浓度的函数,即μeffRk=f(Cp),形式与盐水模型流度分母项相同(方程(8)),因此可通过修改盐水模型黏浓关系的方式等效计算聚合物驱流度,而油藏模拟软件列表式黏浓关系的输入方式为此提供了便利。据此建立了盐水模型等效聚合物流度计算流程(见图1):首先由方程(9)计算一定聚合物溶液浓度下的平均吸附量,而后依据方程(2)得出相应残余阻力系数Rk(也可由方程(10)计算);找出原始黏浓关系中该聚合物浓度对应的黏度特征值,并与Rk相乘得到等效黏度;依此类推,修改并得到了更新的黏浓关系。更新的黏浓关系可完全等效模拟聚合物增黏作用,以及吸附导致的降渗作用,使两者流度计算结果完全相同。
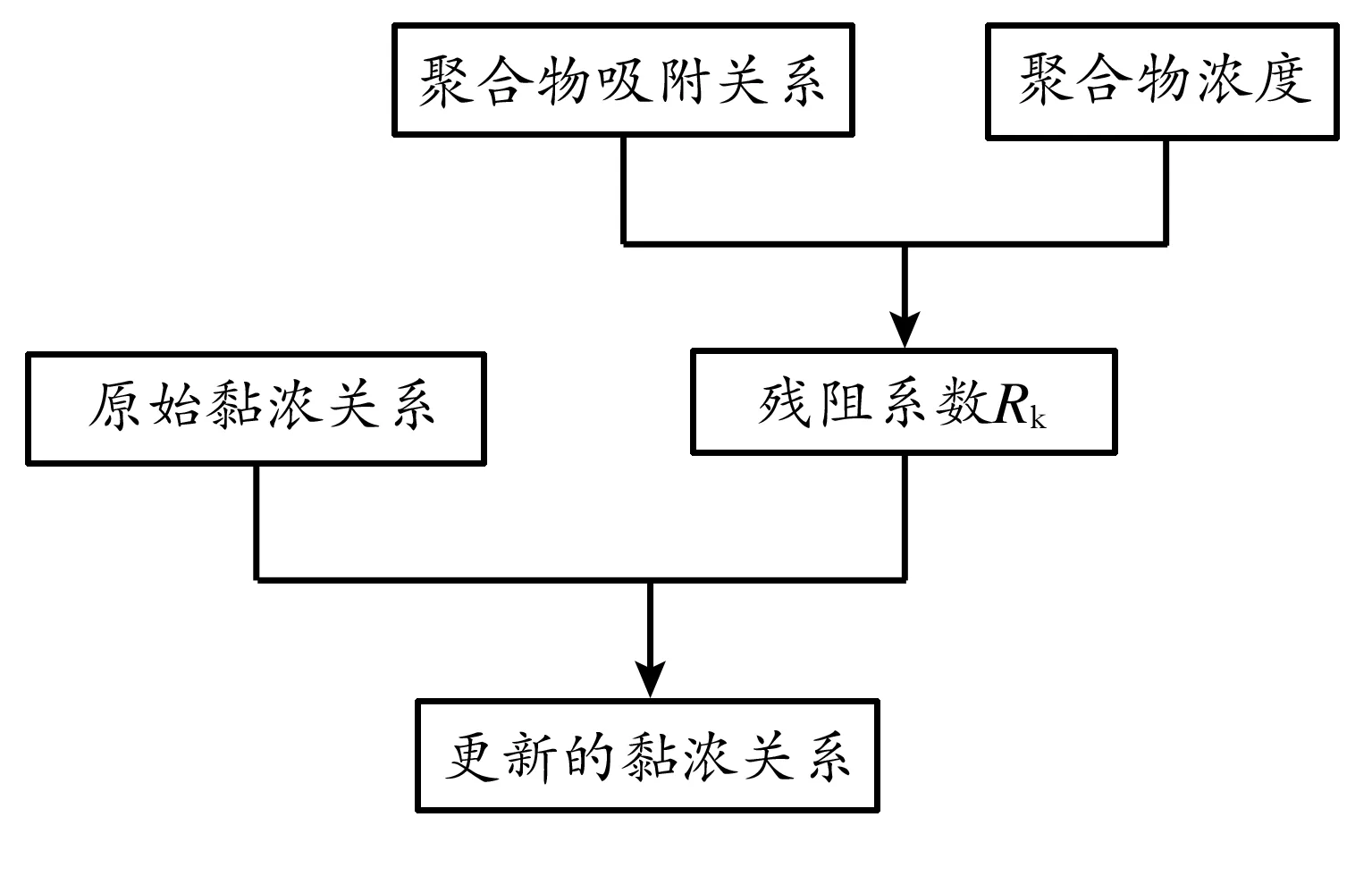
图1 盐水模块等效聚合物驱流度计算流程
Fig.1Equivalentpolymermobilitycalculationflowchartofbrinemodel
忽略不可及孔隙体积与聚合物吸附损失的合理性将在下面“模拟新方法准确性验证”部分进行详细论证。研究发现不可及孔隙体积对聚合物驱模拟结果的影响不显著,且对于矿场聚合物用量范围、吸附损失的影响几乎可忽略不计。
综上,通过对盐水模型的改造构建了聚合物驱等效模拟新方法,该方法可以较全面、合理地表征聚合物驱提高采收率核心机理,即聚合物增黏作用与降低渗透率作用;同时形式上保持了盐水模块,雅可比矩阵非线性程度变化不大,可方便结合现有高速求解算法或“嫁接”至高效数模软件,大幅降低复杂油藏大规模聚合物驱模拟时间成本。
2 准确性验证
这部分将分别从三方面论证聚合物驱模拟新方法的准确性:与传统聚合物驱模拟结果对比;不可及孔隙体积IPV影响的显著性分析;聚合物吸附滞留损失影响的显著性分析。
2.1 与传统聚合物驱模拟结果对比
采用传统聚合物驱模型的软件有很多,如Eclipse聚合物模块。出于时间成本方面的考虑,选取某大型稠油油田一定区域进行模拟对比分析。该区域网格剖分规模为47 740个节点(35×44×31),网格步长70 m×70 m×1.5 m;地层原油黏度100 mPa·s,平均渗透率10 000 mD,孔隙度0.32,油藏温度60 ℃;星型水平井网开发,平均井距550 m;聚合物注入质量浓度1 600 mg/L,目标地层工作黏度10 mPa·s,极限吸附量40 μg/g,极限残余阻力系数RRF为1.60。分别采用聚合物驱模拟新方法、Eclipse Polymer模块进行模拟,虚拟开发结果如图2所示。对比如下生产指标,包括产油量/累积产油量(图2(a))、含水率/生产汽油比(图2(b))、地层注入量/产液量(图2(c)),新方法与传统方法模拟结果吻合度高,预测采收率分别为33.01%、32.95%,两者相差仅0.06%;高峰注入量相对差仅0.16%,从而验证了该方法的准确性。
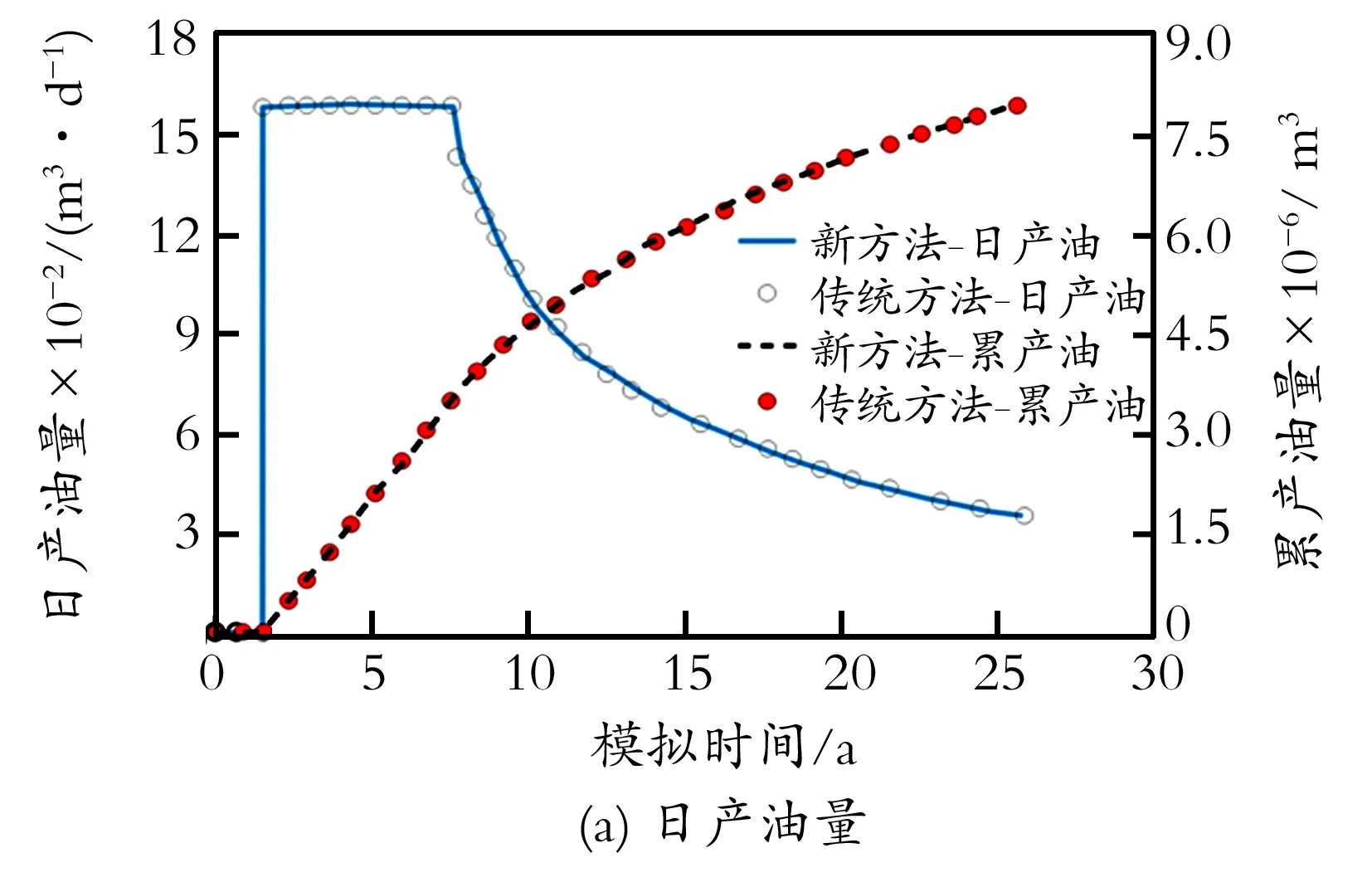
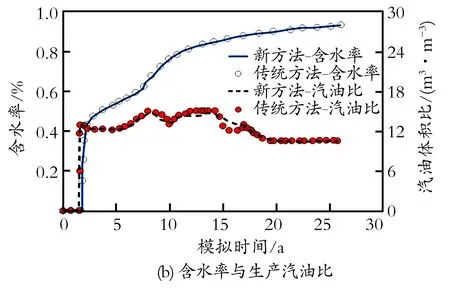
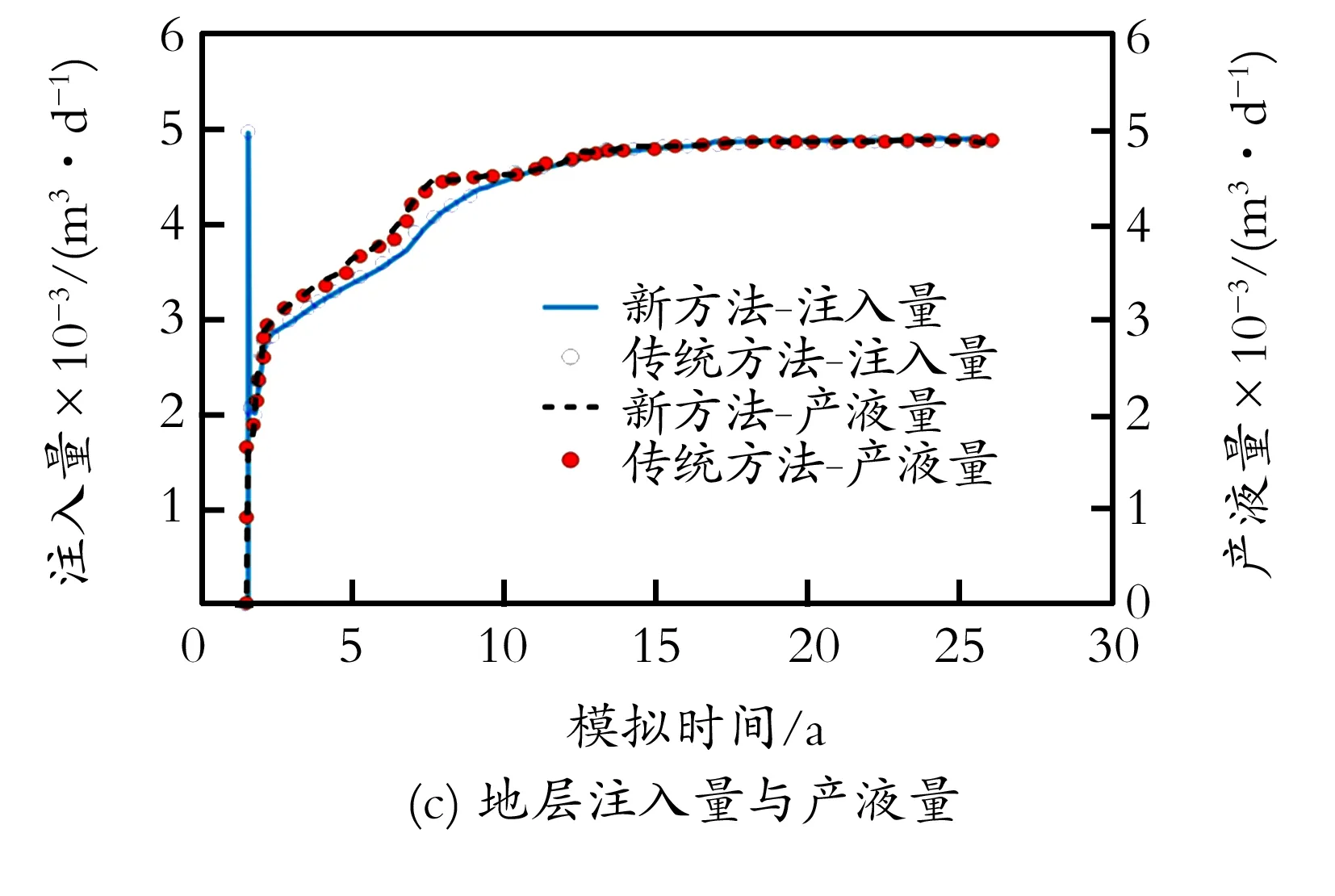
图2 新方法与传统方法聚合物驱模拟结果对比
Fig.2Comparisonsofpolymerfloodresultsbetweennewandtypicalsimulationmethods
2.2 不可及孔隙体积IPV影响的显著性分析
模拟新方法忽略不可及孔隙体积IPV,为检验其合理性,研究IPV对聚合物驱油效果的影响显著性。公开文献报道一般IPV变化在0~0.3[10-11],设置IPV分别为0、0.1、0.2、0.3,相应模拟结果如图3(a)—(c)及表1所示。由图3(a)—(c)及表1可知,当IPV在0~0.3变化时,新方法与传统方法所获得的采油曲线及采收率值几乎相同,累产油相对变化幅度最大值1.41%,对应采收率相差仅0.46%,高峰注入量相对变化范围小于4.4%,聚合物干粉用量相差控制在5.6%以内;含水率曲线几乎相同,仅在前期略有差别。根据拇指法则,IPV对聚合物驱模拟结果的影响不显著,几乎可忽略不计,元福卿等[12-14]研究也得到相似结论。
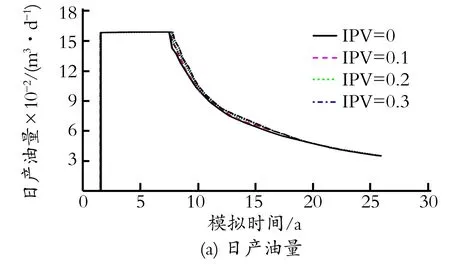
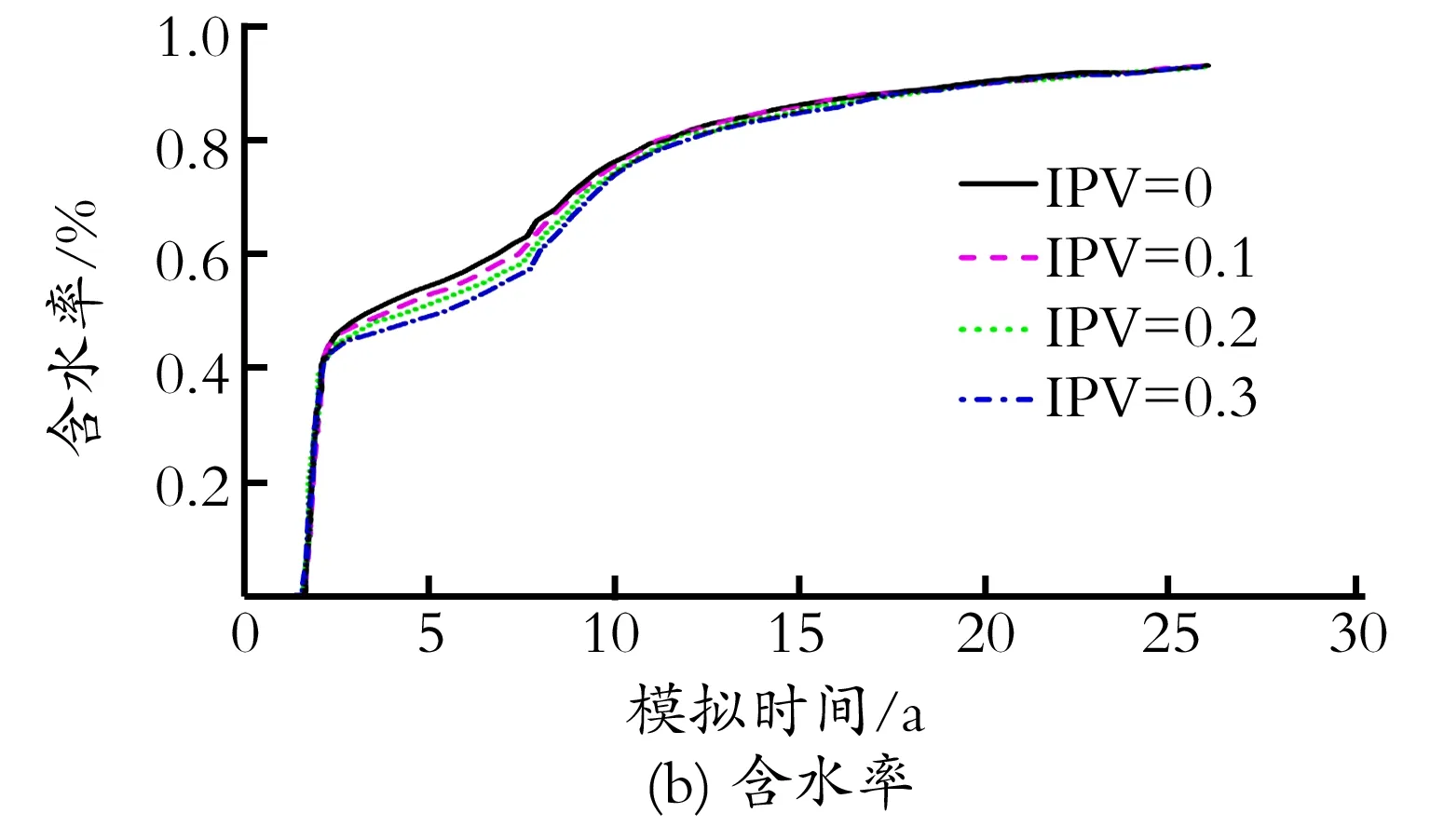
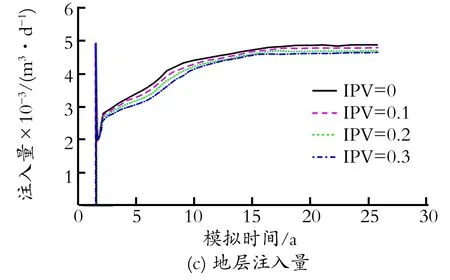
图3 不同IPV条件下聚合物驱模拟结果对比Fig.3 Comparisons of polymer flood results for different IPV
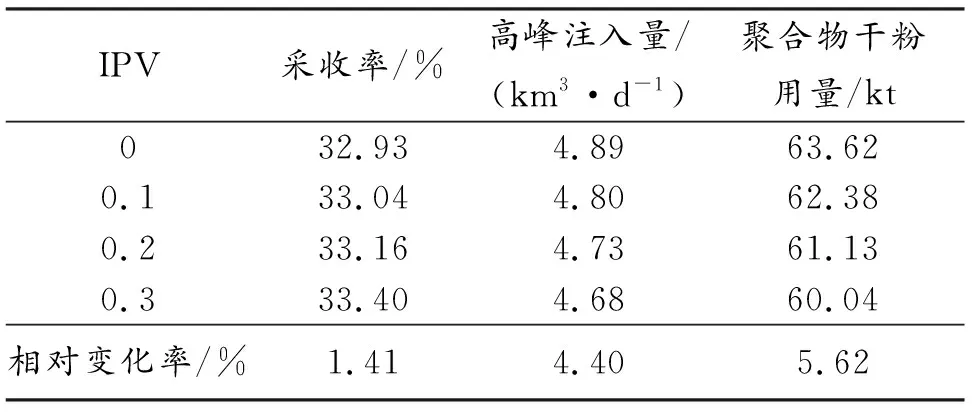
IPV采收率/%高峰注入量/(km3·d-1)聚合物干粉用量/kt032.934.8963.620.133.044.8062.380.233.164.7361.130.333.404.6860.04相对变化率/%1.414.405.62
2.3 吸附滞留损失影响的显著性分析
模拟新方法考虑了聚合物吸附滞留导致的降低渗透率作用,但忽略聚合物本身的吸附滞留损失,下面评估该损失对聚合物驱效果的影响。
引入吸附损失率,定义为聚合物吸附量与总注入量的比值,该值越小,则吸附损失相对越低,对模拟结果的影响越小,新方法越接近于传统方法。由聚合物吸附特征,吸附损失率与聚合物用量有关,见式(11):
(11)
式中,Cu为聚合物用量;ρr为岩石密度。聚合物在岩石与水相之间的质量分布由式(12)确定:
(12)
图4为Sw=0.75时吸附损失率随聚合物用量的变化情况,随着聚合物用量的增加,吸附损失率迅速降低,当聚合物用量为1 600 mg/L·PV时,仅有10%的聚合物被岩石吸附。此变化趋势是由聚合物吸附特征引起的,随着聚合物浓度增加,岩石再吸附能力降低,吸附增长趋缓,逐步达到饱和吸附。
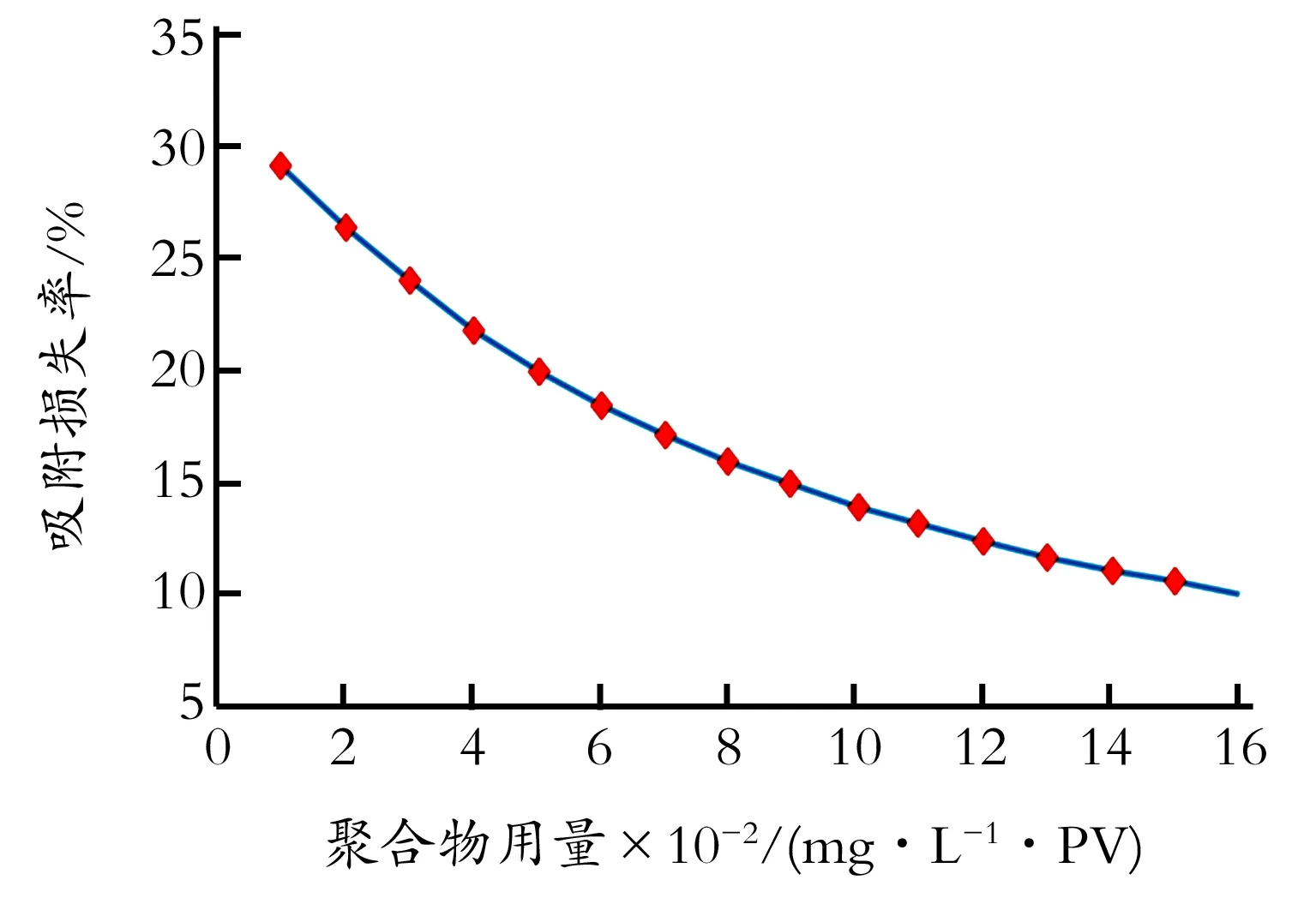
图4 吸附损失率与聚合物用量的关系(Sw=0.75)
Fig.4AdsorptionlossratiovspolymerusageatSw=0.75
聚合物吸附损失率随聚合物用量增大而降低,这意味着模拟新方法与传统方法的差异受到聚合物用量的影响。不同聚合物用量条件下两种方法模拟结果见表2。由表2可知,随着聚合物用量的增大,新方法(忽略吸附损失)预测结果的绝对差异与相对差异均迅速降低,当聚合物用量大于514 mg/L·PV时,两种方法采收率绝对差异低于0.39%、累产油相对差异控制在1.5%以内,尤其是大于1 179 mg/L·PV时,两者几乎已无区别;事实上,即使聚合物用量低至122 mg/L·PV(0.07 PV),新方法预测的相对差异也低于5.0%,仍然满足拇指法则,验证了新方法模拟的高精度。
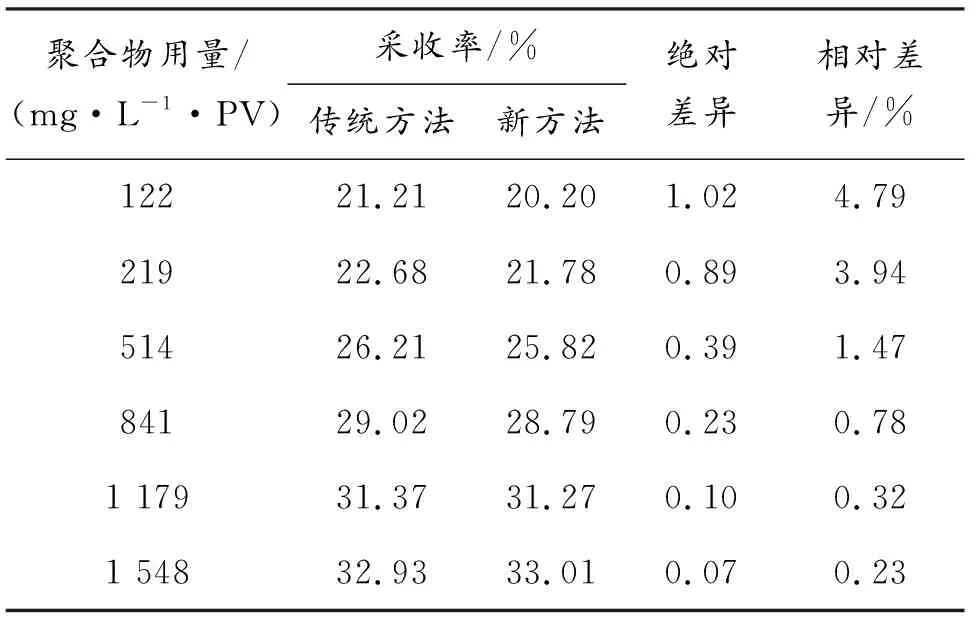
表2 新方法预测差异与聚合物用量之间的关系Table2 Predicated recovery factor discrepancy between new and typical methods
3 模拟新方法的矿场应用
在论证了模拟新方法准确性与适用性的基础上,应用该方法进行全油田大尺度聚合物驱数值模拟。选取上述大型复杂河流相稠油油田作为模拟目标油田,网格剖分规模近500万节点,如采用常规聚合物驱模拟器,经检验16个CPU并行需要耗时518.4 h(21.4 d)才能完成一次虚拟开发模拟(最大时间步长30 d),严重制约了油藏开发决策速度;而采用本文提出的模拟新方法,相同条件下,单次模拟耗时可大幅降低至5.8 h(见图5),计算效率提高近90倍,解决大型复杂油田聚合物驱模拟难题,表明新方法具有很高的应用价值。
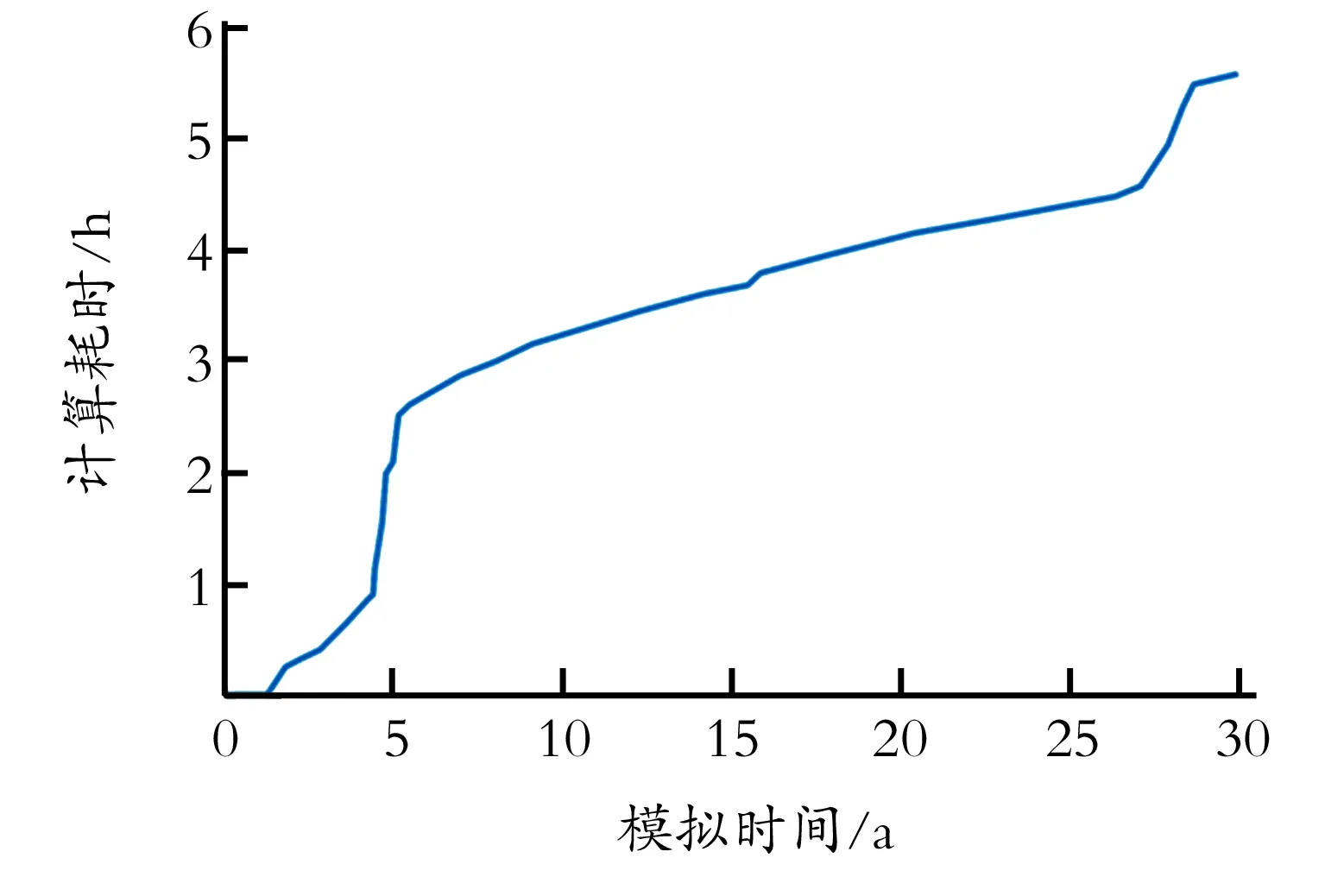
图5 新方法模拟耗时情况
Fig.5TotalCPUtimeoffullfieldsimulationbynewmethod
4 结论
(1) 提出了一种基于盐水模型的聚合物驱高效模拟新方法,该方法能够全面考虑聚合物驱提高采收率关键机理,包括聚合物增黏作用,聚合物吸附滞留造成的降渗作用等。
(2) 新方法有效克服了传统聚驱模拟器计算成本高的不足,胜任百万节点以上大规模复杂油藏聚驱模拟,实例表明可将单次模拟耗时由518.4 h(21.6 d)缩短为5.8 h,计算速度提升近两个数量级,明显提高了油藏开发决策速度,具有较高的应用价值。
(3) 新方法模拟精度高,且精度随着聚合物用量增大而进一步提高,当聚合物用量大于514 mg/L·PV时,预测采收率与传统模拟结果的绝对差异可低于0.4%、相对差异控制在1.5%以内。现有聚合物驱矿场用量一般高于此值,意味着新方法适用于绝大多数聚合物驱项目,应用范围广。
[1] 周守为, 韩明, 向问陶, 等. 渤海油田聚合物驱提高采收率技术研究及应用[J].中国海上油气, 2006, 18(6):386-389.
Zhou S W, Han M, Xiang W T, et al. Application of EOR technology by means of polymer flooding in Bohai oilfields[J]. China Offshore Oil and Gas, 2006, 18(6):386-389.
[2] 孙焕泉. 胜利油田三次采油技术的实践与认识[J].石油勘探与开发, 2006, 33(3):262-266.
Sun H Q. Practice and understanding on tertiary recovery in Shengli oilfield[J]. Petroleum Exploration and Development, 2006, 33(3):262-266.
[3] 王德民, 程杰成, 吴军政, 等. 聚合物驱油技术在大庆油田的应用[J].石油学报, 2005, 26(1):74-78.
Wang D M, Cheng J C, Wu J Z, et al. Application of polymer flooding technology in Daqing oilfield[J]. Acta Petrolei Sinica, 2005, 26(1):74-78.
[4] Wei Z J, Zhang D X. A fully coupled multicomponent, multiphase flow and geomechanics model for enhanced coalbed methane recovery and CO2storage[J]. SPE Journal, 2013, 18(3):1-20.
[5] Cao H, Aziz K. Performance of IMPSAT and IMPSAT-AIM models in compositional simulation[C]//SPE Annual Technical Conference and Exhibition. Dallas:A Society of Petroleum Engineers, 2002.
[6] Wallis J R, Kendall R P, Little T E. Constrained residual acceleration of conjugate residual method[C]//SPE Reservoir Simulation Symposium. Dallas:Society of Petroleum Engineers, 1985.
[7] Saad Y, Schultz M.Gmres:A generalized minimum residual algorithm for solving non-symmetric linear systems[J].Siam Journal on Scientific and Statistical Computing, 1986, 7(3):856-869.
[8] 未志杰, 康晓东, 张贤松, 等. 基于黑油的多组分聚合物驱数学模型[J].中国科学:技术科学,2018, 48(4):415-423.
Wei Z J, Kang X D, Zhang X S, et al. A black-oil-based multi-component model for polymer flooding[J]. Sci. Sin. Tech., 2018, 48(4):415-423.
[9] 张颖苹. 稠油油藏聚合物驱剖面反转现象室内实验[J].特种油气藏, 2016, 23(6):111-114.
Zhang Y P. Laboratory experiment of profile inversion regulation in heavy-oil reservoir with polymer flooding[J]. Special Oil & Gas Reservoirs, 2016, 23(6):111-114.
[10] Schneider F N, Owens W W. Steady-state measurements of relative permeability for polymer/oil systems[J]. SPE Journal, 1982, 22(1):79-86.
[11] Manichand R N, Seright R. Field vs laboratory polymer-retention values for a polymer flood in the Tambaredjo field[J]. SPE Reservoir Evaluation & Engineering, 2014, 17(3):1-12.
[12] 元福卿, 李振泉. 不同因素对聚合物驱效果的影响程度研究[J].西南石油大学学报(自然科学版), 2008, 30(4):98-100.
Yuan F Q, Li Z Q. The influence degree of different factors on the effectiveness of polymer flooding[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2008, 30(4):98-100.
[13] 王正波, 王强, 叶银珠, 等. 多参数约束聚合物驱历史拟合方法[J].石油勘探与开发, 2010, 37(2):216-219.
Wang Z B, Wang Q, Ye Y Z, et al. A multiple-parameter-constraint history matching method for polymer flooding[J]. Petroleum Exploration and Development, 2010, 37(2):216-219.
[14] 章威, 喻高明, 胡海霞, 等. 含水率曲线对聚合物驱特征参数的敏感性分析[J].岩性油气藏, 2012, 24(1):125-128.
Zhang W, Yu G M, Hu H X, et al. Sensitivity analysis of polymer flooding characteristic parameters on water cut curve[J]. Lithologic Reservoirs, 2012, 24(1):125-128.
