计及光伏调压能力的分布式光伏并网机会约束规划方法
2018-06-27孙玲玲贾清泉崔志强
王 宁, 孙玲玲, 贾清泉, 崔志强
(1. 电力电子节能与传动控制河北省重点实验室, 燕山大学, 河北 秦皇岛 066004;2. 河北省仪器仪表工程技术研究中心, 河北 承德 067000)
1 引言
近年来,光伏发电技术及应用发展迅速,采用分布式发电已成为开发利用太阳能资源的主要形式[1]。然而,光伏发电输出功率受外界环境影响,具有随机波动性,其大规模高渗透率接入配电网,改变了原有配电网中的潮流分布,使电压波动变大,电压越限问题突出,这些问题都限制了光伏的接入[2-4]。传统光伏电源按单位功率因数和最大功率跟踪方式工作[5],仅发挥了发电功能。分布式电源并网技术要求(GB/T 33593-2017)提出分布式电源(Distributed Generation,DG)应主动参与配电网调压,并能够根据配电网运行状态调整其输出的有功和无功功率,从而使DG的电压调节功能得以发挥。因此,充分利用分布式光伏的电压无功调节能力,对分布式光伏并网发电进行合理规划,以实现光伏电源的绿色能源供应和参与电压调节双重目标,对于促进电网绿色、健康、可持续发展具有重要意义。
目前,国内外学者开展了分布式光伏发电并网规划的研究工作。文献[5]建立了负荷和分布式光伏电源引起电压偏差与电压波动的计算模型,推导出六种典型负荷分布下线路电压偏差与电压波动不越限时所能允许接入的光伏电源容量极限。文献[6]建立了光伏集中并网后引起并网电压偏差的数学模型,推导出以电压偏差不越限为约束的光伏准入容量,定义了母线电压波动的指标。文献[7]通过计算配电网馈线上所有负荷等级下光伏电源的最大输出功率并结合相关观测数据,得出光伏最大允许接入容量,从而避免出现过电压现象。文献[5-7]的研究均是采用光伏并网准入容量的确定性计算模型,未考虑利用光伏电源的剩余容量进行电压无功调节。文献[8]提出一种适用于考虑负荷和太阳辐射随机变化的并网光伏电站极限容量计算方法,并采用遗传算法和蒙特卡罗模拟的混合算法进行求解。文献[9]提出了一种计及光伏时序性与相关性的主动配电网规划-运行双层机会约束优化模型,其中上层模型考虑主动配电网综合经济成本最优从而决定光伏安装位置与容量,下层模型考虑主动配电网电压运行优化从而决定最佳运行管理策略。文献[10]提出风光双层随机最优潮流优化配置模型,上层模型以配电网投资收益及配电自动化成本年利润最大为目标,以静态安全为机会约束;下层模型以DG有功削减最小为目标,考虑DG有功功率削减限制、有载调压器调节、DG功率因数调节等主动管理措施。文献[11]提出考虑风-光-荷联合时序场景的分布式电源接入容量规划模型,考虑DG出力控制、DG功率因数调节、无功补偿装置投切等主动管理措施,采用联合概率分布法和场景削减技术进行求解。
现有关于光伏接入规划的研究没有考虑光伏发电自身对电网的电压无功支撑能力,使规划结果不够合理。而且,大多文献研究如何确定DG极限接入容量,但在光伏规划建设实践中,待规划区域光伏建设规模往往由外部环境决定,是一个给定值,电网企业需确定如何接入才能更有利于降低光伏接入对电网的不利影响。针对该问题,本文以光伏计划接入量为已知量,以配电网运行网损最小为规划目标,以光伏参与电压无功调节下电压合格为约束条件,建立光伏并网规划模型,得出光伏最优接入容量,即优化配电网中各节点的光伏接入容量,将光伏计划接入量以最合理的方式接入电网。规划模型利用光伏逆变器剩余容量、有载调压器分接头控制及电容器组合投切等无功优化措施对配电网进行调压,建立电压偏差机会约束;针对光伏输出功率的概率分布时序特性,利用中值拉丁超立方抽样 (Median Latin Hypercube Sampling,MLHS) 技术形成光伏与负荷初始时序样本,采用多重积分法和Gram-Charlier级数展开得到配电网节点电压分布机会约束;采用改进的随机权重粒子群算法对模型进行求解。仿真结果表明本文规划方法在保障配电网电压合格的前提下,能够实现光伏计划接入量的最优分配。
2 光伏与负荷随机变量的概率模型
光伏发电输出功率的随机波动性会导致配电网运行面临较高的不确定性,规划中必须充分考虑光伏不确定性的影响。本节首先建立光伏发电与负荷输出功率的概率模型,在此基础上,采用中值拉丁超立方抽样技术形成24个时段光伏与负荷初始时序样本,用于配电网节点电压概率分布计算。
2.1 光伏及负荷的概率模型
太阳辐射强度可认为近似服从Beta分布,结合光伏发电功率输出模型及光照强度概率分布函数,可得光伏功率输出概率密度函数为[12]:
(1)
式中,PPV、Pmax分别为一定时段内光伏电源的随机出力和最大出力;Γ为Gamma函数;α、β为光照强度Beta分布的形状参数。其中,不同时段内Beta分布的形状参数不同。图1为某地区不同时段的形状参数[13]。

图1 不同时段的形状参数Fig.1 Shape parameters at different times
负荷的概率模型在进行概率潮流计算时不可忽略。作为中长期负荷预测结果,负荷概率模型基本符合正态分布[14]。其概率密度函数为:
(2)
(3)
式中,μP、μQ分别为负荷有功、无功功率均值;σP、σQ分别为负荷有功、无功功率方差。不同时段内负荷概率函数的均值和方差不同。
2.2 光伏与负荷输出功率随机变量的分时段采样
针对光伏发电与负荷出力的概率分布函数,本文首先划分时段,然后根据每个时段内特定的概率分布参数,利用改进的MLHS技术[15]得出24个时段光伏与负荷出力的初始时序样本。
假设待规划配电网内共有n个光伏与负荷变量,表示为H=(h1,h2,…,hn),其中有k个服从Beta分布的光伏、n-k个服从正态分布的负荷。利用MLHS技术对某时段服从特定概率分布的光伏和负荷进行采样,过程如下:
(1)设采样规模为M次,F(hi)为变量hi在某个时段内服从特定分布参数的累积分布函数。
(2)将区间[0,1]平均分成M等份,则每个区间的概率均为1/M,并选取每个区间的中间值。
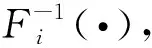
(4)

(4)当向量H中所有变量采样完成后,得到某个时段向量H对应的n×M阶样本矩阵。光伏与负荷的时序样本形成过程如图2所示。
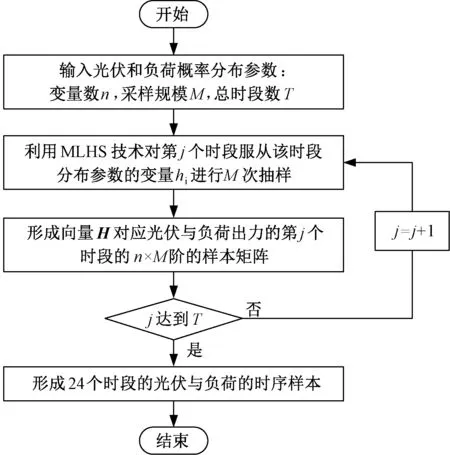
图2 光伏发电与负荷时序样本生成流程图Fig.2 Flow chart of timing sequence samples generation for PV and load
3 计及光伏出力分布时序特性的配电网概率潮流计算
由第2节得到的光伏与负荷时序样本作为输入量,利用概率潮流法计算配电网节点电压统计信息,将所得信息作为求取光伏接入容量的约束条件。随机变量的概率特性可由各阶矩近似表示[16],为得到配电网节点电压的分布特征,需进一步求解配电网节点电压的各阶矩。本文采用多重积分逼近法简化求解配电网节点电压的各阶统计矩。
3.1 配电网节点电压各阶矩求取
假定输出是输入的多元函数y(x1,x2,…,xn),则光伏输出功率的联合概率分布为[17]:
(5)

(6)
式(6)是多变量的多重积分算式,参考文献[17],利用多重积分逼近法对式(6)进行求解。
已知Stroud积分公式为:
(7)
式中,Ai为权系数;vi1,vi2,…,vin为配点。
记多项式函数g(s1,s2,…,sn)为输入乘积多项式之和,且每个乘积多项式如式(8)和式(9)所示:
(8)
(9)
式中,C为常数;当函数g中各输入的乘积多项式均满足式(9),且能达到最大值时,称C为函数g的阶次;若式(9)中小于等于C阶的多项式函数都成立时,则称积分公式具有C阶代数精度。不同代数精度公式的选择具体详见文献[17],这里不再赘述。其中,3阶代数精度对应的配点及权系数为:
(10)
式中,FS为全排列得到的点。将上述参数代入式(6)即可求出配电网节点电压的各阶矩。
本文采用多重积分法对配电网概率潮流进行求解,该方法仅需对少数输入量进行潮流计算,相比于传统概率潮流求解方法的点估计法,可以提供更高的代数精度公式;相比于半不变量法,可以直接处理非线性的输入输出关系,而不需要对潮流方程进行线性化处理。
3.2 Gram-Charlier级数展开
求得配电网节点电压u的各阶矩后,利用Gram-Charlier级数展开求其概率分布值。
设连续随机变量x的均值和方差分别为μx、σx,该随机变量的标准形式为ξx=(x-μx)/σx。其概率分布函数Fξ(x)和概率密度函数fξ(x)可由Gram-Charlier级数展开计算得到[18]:
式中,Φ(x)和φ(x)分别为标准正态分布的概率分布函数和概率密度函数;n表示Φ(x)和φ(x)的第n阶导数;g为系数。Gram-Charlier级数展开的系数可由ξx的n阶中心矩多项式表示[19]:
(13)
式中,β3、β4分别为ξx的3阶和4阶中心矩。
采取有限阶的级数展开可以使计算结果更加精确,故在此仅计算x的方差、ξx的3阶和4阶中心矩。
3.3 配电网概率潮流计算过程
配电网概率潮流能够计算输入为随机变量时输出变量的概率信息。本文将光伏出力概率分布时序特性与配电网概率潮流计算相结合,具体计算过程如下:
(1)建立光伏发电及负荷输出功率概率模型。
(2)利用MLHS技术对某时段服从特定概率分布的光伏与负荷输出随机变量进行处理,形成24个时段光伏与负荷的时序样本。
(3)将时序样本作为输入变量,利用多重积分算式(6),计算配点和权系数。
(4)由步骤(2)得到的输入变量,计算满足式(9)的多重积分公式配点对应的实际输入量。
(5)将步骤(4)得到的实际输入量带入潮流方程,得到对应输出量。
(6)根据式(6),计算输出量的各阶矩。
(7)利用Gram-Charlier级数展开得到输出变量的概率密度分布曲线。
4 光伏并网最优接入容量规划模型
4.1 机会约束规划模型
本文建立光伏发电规划模型的基本思想是在制定光伏最优接入方案的基础上进一步考虑配电网运行过程中光伏发电参与电压调节的能力。以系统总网损最小为目标函数,规划过程耦合运行无功优化手段,利用光伏发电剩余容量、有载调压器分接头控制及电容器组投切三种无功优化手段对系统进行无功电压调节,使配电网电压指标满足一定的合格率,从而实现充分考虑并利用光伏发电资源的可调潜力,改善系统电压分布,降低网络损耗,提高配电网的光伏并网接纳能力。
4.1.1 目标函数
本文的规划目标是在待规划光伏接入容量一定的基础上充分考虑光伏的无功调压能力,以系统总网损最小为目标从而确定分布式光伏最优接入容量,目标函数如下:
(14)
式中,Ploss.i.t为第t个时段系统中节点i的网损;N为系统总节点数。
设光伏接入配电网第i个节点,则第t个时段接入点处的有功功率Pi.t和无功功率Qi.t可表示为:
Pi.t=PG.i.t+PPV.i.t-PL.i.t
(15)
Qi.t=QG.i.t+QPV.i.t+QC.i.t-QL.i.t
(16)
式中,PG.i.t、QG.i.t分别为第t个时段电网向节点i注入的有功功率、无功功率;PPV.i.t、QPV.i.t分别为第t个时段节点i接入的光伏有功功率、无功功率;QC.i.t为第t个时段节点i接入的电容器组合容量;PL.i.t、QL.i.t分别为第t个时段节点i接入负荷的有功功率、无功功率。
式(16)中QPV.i.t为由光伏逆变器剩余容量决定的光伏无功出力,存在如下关系:
(17)
式中,SPV.i为节点i接入的光伏电源总容量;QPV.i.t.max和QPV.i.t.min分别为节点i接入光伏电源无功出力的上、下限,负值表示从系统吸收无功功率。
当分布式光伏发电接入系统后,全时段的系统网损为[20]:
(18)
式中,Pj.t、Qj.t分别为第t个时段节点j注入的有功功率和无功功率;αij和βij分别为:
(19)
(20)
式中,Ui、Uj分别为系统节点i、j的电压;γij为节点i、j间馈线电阻。
4.1.2 配电网潮流等式约束
(21)
式中,A(i)为节点集合;δij.t为第t个时段电压相角差;Gij、Bij为网络导纳。
4.1.3 配电网电压合格机会约束
配电网电压受光伏接入影响呈现概率特性。如果采用确定性约束条件,即要求所有情况下系统电压都满足要求,则光伏发电接入容量会受到极大的限制。将含有光伏发电的配电网电压越限不等式约束表示为机会约束形式的电压合格率约束。因此,本文机会约束使配电网在随机因素影响下的电压满足:
(22)
式中,PU.p为合格事件的概率;ξ为置信水平(合格率要求),0<ξ≤1,ξ越接近1则表示对合格率要求越严格,ξ=1表示不允许指标越限。依据电网实际要求,可选取适当的置信水平ξ,一般取0.90~ 0.99之间[4]。
4.1.4 无功优化不等式约束
本文在规划过程中充分计及配电网无功优化策略,利用光伏发电剩余容量、有载调压器分接头调节及电容器组投切对配电网进行无功优化。无功补偿措施不等式约束如下。
9.持续开展“减证便民”行动。切实组织做好证明事项清理工作,对民营企业在中国法律服务网“群众批评——证明事项清理投诉监督”平台反映的问题、提出的批评意见,及时督促有关地方和部门抓紧取消违法设定的证明事项,切实避免民营企业办事难、办事慢、多头跑、来回跑、不方便等问题,对于普遍性问题,及时通过法定程序从制度上加以解决。2018年年底前,率先在司法行政系统通过告知承诺、信息共享等方式取消不必要的证明事项。
(1) 光伏逆变器剩余容量约束
QPV.t.min≤QPV.t≤QPV.t.max
(23)
式中,QPV.t为t时刻单个光伏逆变器剩余容量;QPV.t.max、QPV.t.min分别为t时刻单个光伏逆变器剩余容量的上、下限值。
(2) 有载调压器二次侧电压上下限约束
UOLTC.s.min≤UOLTC.s≤UOLTC.s.max0 (24) 式中,UOLTC.s为第s个有载调压器的二次侧电压;UOLTC.s.min和UOLTC.s.max分别为其下限和上限;smax为系统最大接入有载调压器的个数。 (3) 电容器投切组数上下限约束 0≤NC.t≤NC.max (25) 式中,NC.t为电容器投切组数;NC.max为最大投切组数。 (4) 有载调压器和电容器组投切次数约束 有载调压器和电容器作为离散型决策变量,在单个运行周期内操作次数具有严格限制,且每一次投切都是成组操作。有载调压器和电容器组应该满足如下约束条件: (26) (27) DT.t+1-DT.t≤ND_T.max (28) 式中,m为时段总数;DC.t、DC.t+1分别为t时段和t+1时段电容器投切档位;ND_C为电容器开关最大允许投切次数;DT.t、DT.t+1分别为t时段和t+1时段有载调压器投切档位;ND_T为有载调压器的最大允许动作次数;ND_T.max为分接头的相邻时段最大调节档位数。 4.1.5 光伏计划接入容量等式约束 根据规划前期光伏计划接入总容量的决策,光伏计划接入容量等式约束为: (29) 式中,SPV.i为节点i待安装的光伏接入容量;SPV.plan为光伏计划接入的总容量。 4.1.6 单点光伏接入容量约束 配电网线路载流量等条件约束使得单个节点安装的光伏最大接入容量需满足如下约束: 0≤SPV.i≤SPV.i.max (30) 式中,SPV.i.max为节点i处光伏接入容量上限。 针对4.1节光伏并网最优接入容量规划模型,本文采用改进的随机权重粒子群算法进行优化求解。其中优化变量粒子为配电网各节点接入的光伏发电容量,变量维数为光伏并网数量。 在迭代的过程中,通过随机权重w的计算式随机生成粒子的速度与位置。如果粒子的初始位置与最优位置接近,则产生较小的权重w,使粒子快速找到最优位置;如果在初始阶段无法快速找到最优位置,而w的随机生成可以克服该局限。因此,该算法具有兼顾全局与局部的搜索能力。随机生成的w计算公式为: (31) 式中,rand(0,1)表示0~1之间的随机数;N(0,1)表示标准正态分布随机数;μ为随机权重的平均值;σ为随机权重的方差;μmin为最小随机权重平均值;μmax为最大随机权重平均值。 模型求解步骤如下: (1) 输入电力网络元件参数与算法参数,随机权重的粒子群算法种群规模为50,迭代次数为100,最小随机权重平均值μmin=0.5,最大随机权重平均值μmax=0.8,随机权重的方差σ=0.2。 (2) 每个粒子对应光伏并网接入容量的一个方案。根据光伏接入位置,随机生成每个粒子,重复若干次得到初始粒子群体。利用第3节配电网概率潮流计算并统计输出变量的特性,形成并求解具有惩罚项的目标函数,计算出每个粒子的目标函数值,经过比较后,得出最优粒子的位置。 (3) 由式(31)计算w值,进而更新各粒子速度与位置。由概率潮流计算得出各粒子的目标函数值,并与前次迭代结果进行比较,更新并记录各粒子中最大目标函数值与粒子的最优位置。 (4) 若满足迭代次数则终止,输出最优结果。否则返回步骤(3)重复迭代。 本文选取IEEE33节点系统进行算例仿真分析,系统结构如图3所示。电压等级为12.66kV,节点电压范围为0.95~1.05pu,置信水平为0.9,光伏计划接入量为2600kW,节点光伏并网容量上限为1000kW,并网待选节点为7、12、24、31。在节点0和节点1之间接入一台有载调压器,变比范围为0.95~1.05,共9档,调节步长为1.25%;在节点17和节点32分别接入一组无功补偿电容器组,容量为150kVar×8。光伏与负荷出力的概率分布参数参考文献[12-14]。 图3 IEEE33节点系统结构图Fig.3 IEEE33 node system structure diagram 为分析光伏出力概率分布时序性对规划结果的影响,本文通过划分24个时段来计算全时段的优化结果,并与单个时段优化结果进行对比。全时段与第7个时段、第12个时段优化对比结果如表1所示。 表1 光伏出力概率分布时序性对规划结果的影响Tab.1 Influence of probability distribution timing sequence of PV power distribution on planning results 由表1可知,当光伏概率分布为整个24时段的参数时,节点电压偏差最小;光伏概率分布为第12时段参数时,光伏并网接入总容量最大。概率分布为第7时段参数时,光伏并网接入总容量最小。分析原因可知,综合考虑24个时段概率分布特性,能计及不同时段光伏输出功率概率分布的时序特性,因此电网运行中电压水平最优;仅考虑单个时段时,不能计及光伏输出功率的时序差异性,仅能按照此时段的参数进行优化,而第12时段光伏出力最大,第7时段光伏出力偏小,所以光伏并网总容量分别在各自时段为最大与最小值。上述结果说明本文在对光伏规划时计及其时序特性与非时序性模型相比,降低了系统运行的电压偏差。 光伏发电规划模型的电压机会约束中置信水平ξ大小表示规划结果的可信程度,不同置信水平选取将对规划结果产生影响。本文选取电网节点电压机会约束的不同置信水平,计算光伏发电并网最优接入容量,结果如表2所示。 由表2可知,随着置信水平ξ的提高,光伏并网接入容量逐渐减小。其原因为随着置信水平ξ的增大,对约束条件中电压质量的要求更加严格,因此光伏并网接入容量减小。 表2 不同置信水平下光伏发电并网最优接入容量Tab.2 Optimal access capacity of PV grid-connected at different confidence levels 5.3.1 光伏无功支撑能力对电网电压的影响 为揭示光伏发电逆变器剩余容量对系统电压调节的能力,图4对比分析了计及和未计及光伏无功调压能力的系统各节点电压偏差分布情况。 图4 不同光伏并网规划方案的节点电压偏差分布Fig.4 Node voltage deviation distribution of different PV grid planning schemes 由图4结果分析可知,在允许光伏逆变器向电网输出无功功率的情况下,系统电压质量得到了明显的改善。系统未接入光伏发电前,各节点电压偏差并不明显,光伏接入后,其附近节点电压上升。由此说明,本文采用光伏逆变器剩余容量对电网进行无功电压调节能够明显改善电网电压质量。 5.3.2 不同规划方案对比分析 为研究不同规划方案对光伏并网容量的影响,本文设置5种不同规划方案进行对比分析,规划方案设置情况如表3所示。由表3不同规划方案得到的光伏并网最优接入容量结果如表4所示。 表3 不同规划方案设置情况Tab.3 Setting of different planning schemes 表4 不同规划方案光伏发电并网最优接入容量Tab.4 Optimal access capacity of PV grid-connected at different planning schemes 由表4分析可知,方案2~5相比于方案1,光伏并网接入容量有所提升,说明规划过程考虑无功优化措施能够提升光伏并网容量;而不同的无功优化措施对光伏并网容量的提升水平不同,其中利用光伏逆变器剩余容量相比于其他2种无功优化策略对光伏接入容量的效果较明显。方案5同时采用了3种无功优化措施,光伏接入容量较其他4种情况最多,表明采用多种无功优化措施比单独采用一种措施更有利于提高系统接纳光伏的能力。 本文提出计及调压能力的分布式光伏发电机会约束规划模型。所建规划模型充分考虑系统运行无功优化措施,利用分布式光伏逆变器剩余容量、有载调压器分接头控制及无功补偿电容器组的优化配合对电网进行调压;以配电网网损最小为目标,配电网各时段电压偏差为机会约束,对光伏发电进行接入容量优化。得到如下结论: (1) 本文提出的光伏规划模型充分考虑了光伏输出功率概率分布的时序特性,规划结果不仅降低了系统电压偏差,还有效提高了光伏并网渗透率。 (2) 本文提出的基于机会约束的规划模型与确定性规划模型比较,可有效避免小概率事件的负面影响,光伏接入容量得到明显提升。 (3) 在光伏并网规划过程中,计及光伏逆变器剩余容量、有载调压器及电容器组投切的无功优化措施。相比于常规规划方法,本文所提计及调压能力的分布式光伏发电机会约束规划模型能够充分发挥光伏无功调压的电网辅助服务能力,改善电网电能质量,促进了可再生能源的消纳。 参考文献(References): [1] 刘振亚(Liu Zhenya). 智能电网技术(Smart grid technology)[M]. 北京:中国电力出版社(Beijing: China Electric Power Press),2010. 168-185. [2] 吴杰,赵凡凡,赵丽霞(Wu Jie, Zhao Fanfan, Zhao Lixia).考虑光伏逆变器剩余容量的配电网无功优化(Reactive power optimization in distribution network considering residual capacity of photovoltaic inverter[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2017,36(1):38-43. [3] 刘健,黄炜(Liu Jian, Huang Wei). 无协调控制条件下分布式光伏电源的可接入容量分析(Analysis about access capacity of distribute photovoltaic power generation under uncoordinated control)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2017,36(3):8-15. [4] 王宁,高朋,贾清泉,等(Wang Ning, Gao Peng, Jia Qingquan, et al.). 光伏并网系统参与电压调节的有功和无功协调控制策略研究(Research on active and reactive power coordination control strategy of PV grid-connected system for voltage regulation)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2017,36(8):23-29. [5] 黄炜,刘健,魏昊焜,等(Huang Wei, Liu Jian, Wei Haokun, et al.). 分布式光伏电源极端可接入容量极限研究(Extreme capacity limitations of photovoltaic generators in distribution grids)[J]. 电力系统保护与控制(Power System Protection and Control),2015,43(3):22-28. [6] 王璟,蒋小亮,杨卓,等(Wang Jing, Jiang Xiaoliang, Yang Zhuo, et al.). 光伏集中并网电压约束下的准入容量与电压波动的评估方法(Penetration capacity under voltage constraint and evaluation methodology of voltage fluctuation caused by centralized grid connection of photovoltaic power)[J]. 电网技术(Power System Technology),2015,39(9):2450-2457. [7] 范元亮,赵波,江全元,等(Fan Yuanliang, Zhao Bo, Jiang Quanyuan, et al.). 过电压限制下分布式光伏电源最大允许接入峰值容量的计算(Peak capacity calculation of distributed photovoltaic source with constraint of over-voltage)[J]. 电力系统自动化(Automation of Electric Power Systems),2012,36(17):40-44. [8] 王一波,许洪华(Wang Yibo, Xu Honghua). 基于机会约束规划的并网光伏电站极限容量研究(Research of capacity limit of grid-connected photovoltaic power station on the basis of chance-constrained programming)[J]. 中国电机工程学报(Proceedings of the CSEE),2010,30(22):22-28. [9] 贾清泉,赵美超,孙玲玲,等(Jia Qingquan, Zhao Meichao, Sun Lingling, et al.). 主动配电网中计及时序性与相关性的分布式光伏并网规划(Planning for grid-connection of distributed PVs considering the sequential feature and correlation in active distribution network)[J]. 中国电机工程学报(Proceedings of the CSEE),2018, 36(6): 1719-1728. [10] 马瑞,金艳,刘鸣春(Ma Rui, Jin Yan, Liu Mingchun). 基于机会约束规划的主动配电网分布式风光双层优化配置(Bi-level optimal configuration of distributed wind and photovoltaic generations in active distribution network based on chance constrained programming)[J]. 电工技术学报(Transactions of China Electrotechnical Society),2016,31(3):145-154. [11] 陈碧云,闭晚霞,李欣桐,等(Chen Biyun, Bi Wanxia, Li Xintong, et al.). 考虑风-光-荷联合时序场景的分布式电源接入容量规划策略(Capacity planning strategies for distributed generation considering wind-photovoltaic-load joint time sequential scenarios)[J]. 电网技术(Power System Technology),2018, 42(3): 755-761. [12] 王成山,郑海峰,谢莹华,等(Wang Chengshan, Zheng Haifeng, Xie Yinghua, et al.). 计及分布式发电的配电系统随机潮流计算(Probabilistic power flow containing distributed generation in distribution system)[J]. 电力系统自动化(Automation of Electric Power Systems),2005,29(14):39-44. [13] 邓威,李欣然,李培强,等(Deng Wei, Li Xinran, Li Peiqiang, et al.). 基于互补性的间歇性分布式电源在配网中的优化配置(Optimal allocation of intermittent distributed generation considering complementarity in distributed network)[J]. 电工技术学报(Transactions of China Electrotechnical Society),2013,28(6):216-225. [14] 刘健,徐精求,董海鹏(Liu Jian, Xu Jingqiu, Dong Haipeng). 配电网概率负荷分析及其应用(Probabilistic load flow analysis of distribution network and its application)[J]. 电网技术(Power System Technology),2004,28(6):67-75. [15] 黄煜,徐青山,卞海红,等(Huang Yu, Xu Qingshan, Bian Haihong, et al.). 基于拉丁超立方采样技术的半不变量法随机潮流计算(Cumulant method based on Latin hypercube sampling for calculating probabilistic power flow)[J]. 电力自动化设备(Electric Power Automation Equipment),2016,36(11):112-119. [16] 张喆,李庚银,魏军强(Zhang Zhe,Li Gengyin, Wei Junqiang). 考虑分布式电源随机特性的配电网电压质量概率评估(Probabilistic evaluation of voltage quality in distribution networks considering the stochastic characteristic of distributed generators)[J]. 中国电机工程学报(Proceeding of the CSEE),2013,33(13):150-156. [17] 吴巍,汪可友,李国杰,等(Wu Wei, Wang Keyou, Li Guojie, et al.). 计及光伏发电相关性的多重积分法概率潮流计算(Probabilistic load flow calculation method based on multiple integral method considering correlation of photovoltaic generation)[J]. 中国电机工程学报(Proceedings of the CSEE),2015,35(3):568-575. [18] 董雷,程卫东,杨以涵(Dong Lei, Cheng Weidong, Yang Yihan). 考虑支路随机断线的概率潮流方法及应用(Probabilistic load flow method with consideration of random branch outages and its application)[J]. 电力系统保护与控制(Power System Protection and Control),2010,38(20):79-84. [19] 杜文娟,卜思齐,王海风,等(Du Wenjuan, Bu Siqi, Wang Haifeng, et al.). 考虑并网风电随机波动的电力系统小干扰概率稳定性分析(Effect of stochastic variation of grid-connected wind generation on power system small-signal probabilistic stability)[J]. 中国电机工程学报(Proceedings of the CSEE),2011,31 (Suppl.):7-11. [20] 杨俊友,崔嘉,田艳丰,等(Yang Junyou, Cui Jia, Tian Yanfeng, et al.). 计及网损最小的含分散式风电场配电网多目标优化策略(Multi-objective optimization strategy of distribution network containing dispersed wind farm considering minimum network loss)[J]. 电网技术(Power System Technology),2015,39(8):2141-2147.4.2 模型求解
5 算例分析
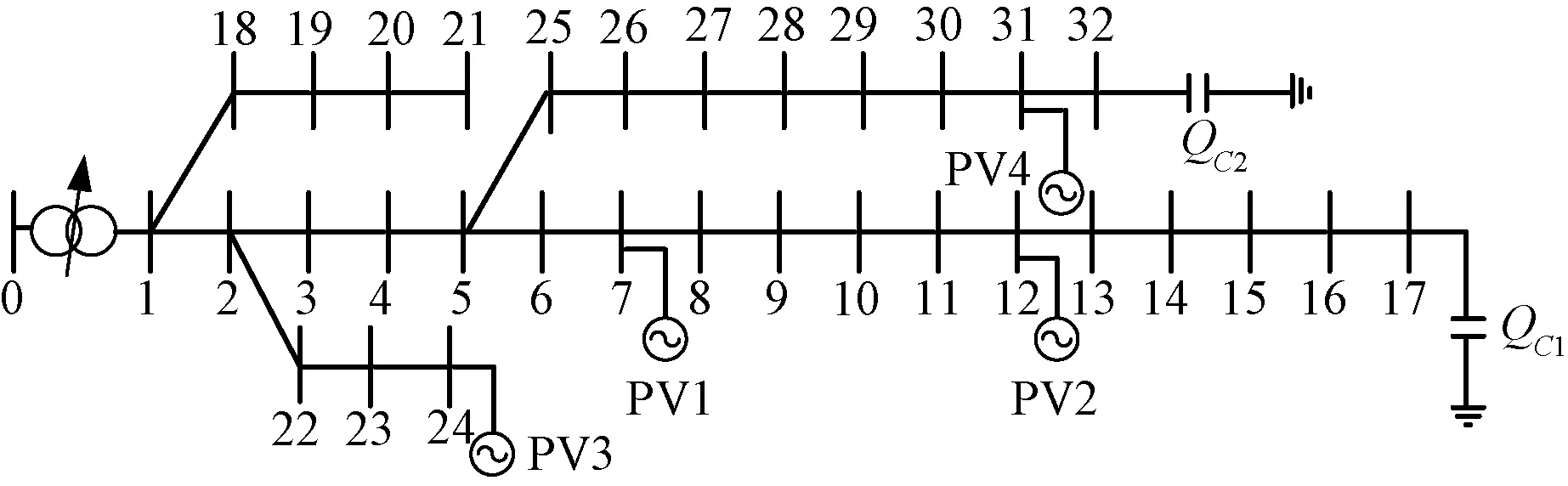
5.1 光伏出力概率分布时序性对规划结果的影响

5.2 不同机会约束置信水平下光伏接入容量分析

5.3 无功优化措施对规划结果的影响

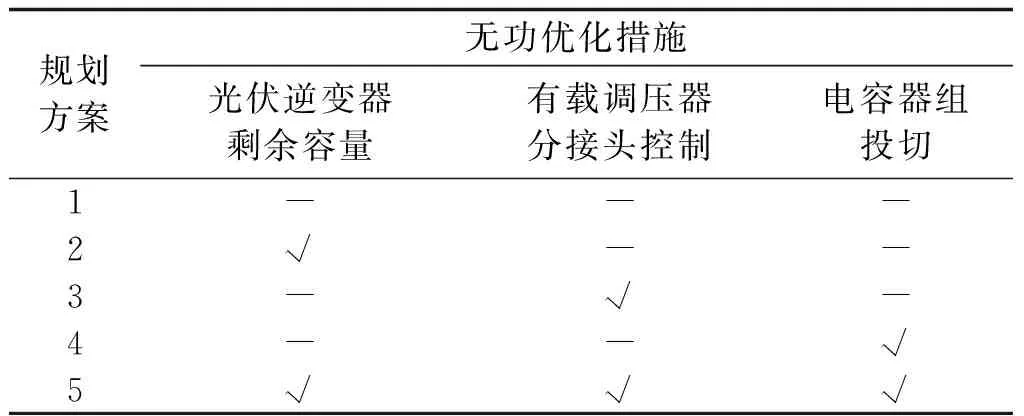

6 结论
