微电网中功率管理与潮流控制方法

张纯江， 吕道正， 董 杰， 王晓寰

(电力电子节能与传动控制河北省重点实验室， 燕山大学电气工程学院， 河北 秦皇岛 066004)

1 引言

微电网概念最先是由美国CERTS(The Consortium for Electric Reliability Technology Solutions)提出的，它作为一个能够独立运行的小型发配电系统，既能与外部大电网并网运行，又能独立运行为本地负载供电[1,2]，近年来获得了极大的关注。微电网作为一个新型的发电系统，首先应该维护其自身系统的稳定，维持自身电压与频率的稳定，满足系统内用户的需求。微电网的安全稳定运行，离不开微电网的控制，控制问题是微电网的一项关键技术，也是一个难点问题。微电网的控制包括对微源的控制和对整个微电网的控制。美国R. H. Lasseter首次提出了微电网中的两种有功功率控制方法，即UPC(Unit output-Power Control)控制和FFC(Feeder Flow Control)控制[3,4]。

文献[5,6]提出的自调节下垂控制策略是微电网功率协调控制的主要方法，该控制策略减小了无功环流，但是其只适用于孤岛微电网，当微电网并网时，需要切换到PQ控制。文献[7]提出的基于背靠背逆变器的微电网功率管理和潮流控制策略，有效实现了微电网和大电网之间潮流恒定，该方法虽然实现了微电网的可控性，但是增加了两个背靠背逆变器，同时就会增加系统的成本和损耗。文献[8]提出的控制策略可以有效实现微电网和公网之间潮流的恒定，同时减小脱网时微网系统的频率跌落，但是该策略并没有考虑到当DG1本地负载增加时，微电网和公网之间的馈线潮流将不能维持恒定，违背了该控制方法的初衷。文献[9,10]根据DG的不同连接方式组成微电网串并联结构，将微电网的串并联结构与UPC和FFC控制方式组合，分析了每种不同组合方式在并网、孤岛和脱网模式下DG的输出功率和系统频率的变化情况。

与传统下垂控制相比，UPC和FFC控制方式具有以下优点：①不需要微电网在并网和孤岛运行时切换DG的控制方式；②并网时，DG采用FFC控制方式可以实现微电网和大电网之间馈线潮流的恒定，微电网内负载变化时，功率由微电网内DG提供，不影响馈线潮流，微电网接入不影响大电网的稳定运行；③孤岛运行时，只要工作在FFC模式下的DG不达到最大输出功率，系统频率就可以维持恒定[11]。

但该控制策略也有其自身的不足。并网时微电网和大电网之间馈线潮流恒定和孤岛时系统频率稳定的前提是微电网中第一个与大电网连接的DG必须采用FFC控制，并且该DG的输出功率没有达到其最大值。而并网时增加微电网和大电网之间的馈线潮流可以缓解峰值负荷时对该DG的功率要求，但是馈线潮流过大会使微电网脱网时频率偏差增大，甚至超出系统的允许范围，对微电网中的负荷产生不利影响。

为了解决上述矛盾本文提出了一种功率协调控制策略，可以实现并网运行时馈线潮流值最小且可控，脱网时系统频率跌落最低，孤岛时系统频率保持不变，最终实现了微网中各DG之间的功率协调控制。

2 DG的两种控制方式

本节主要介绍FFC和UPC两种控制方式的特点和工作原理[12,13]，其工作原理如图1所示，下垂特性曲线如图2所示。

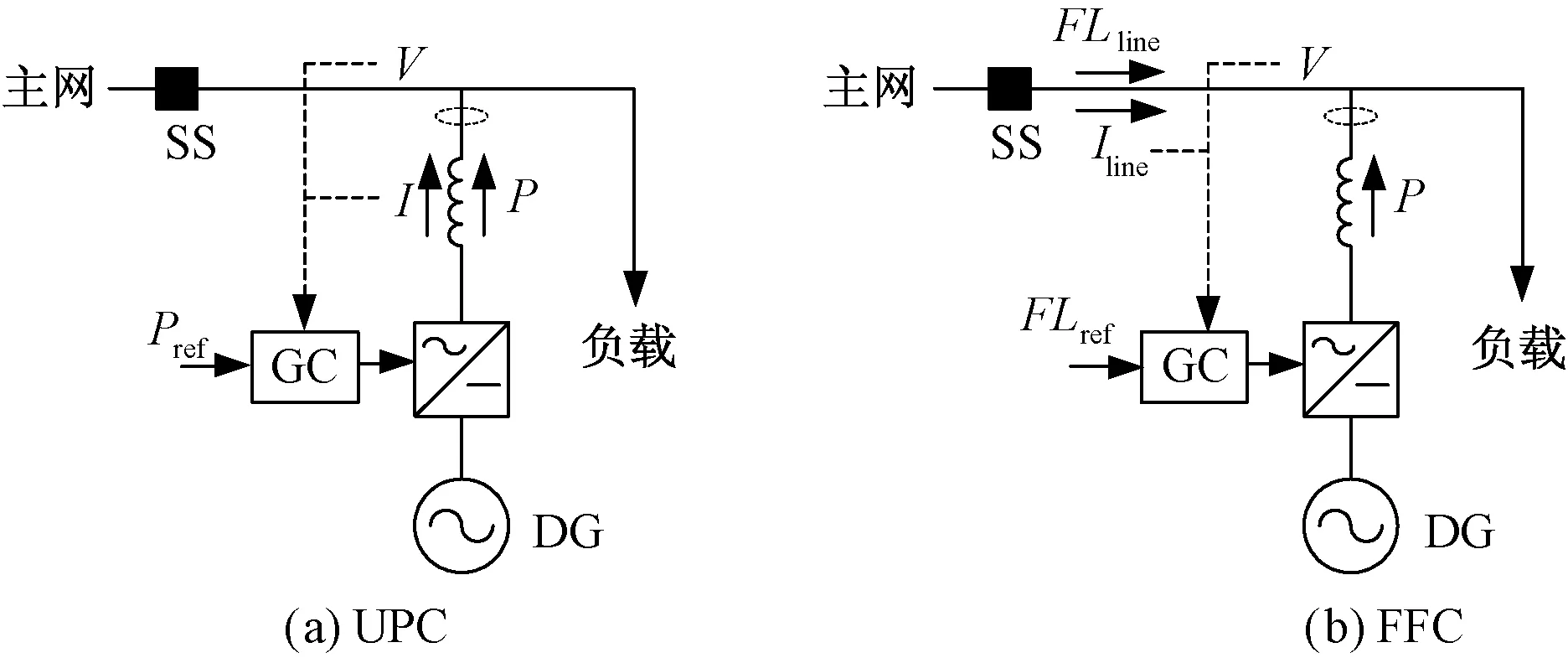
图1 DG的功率控制模式Fig.1 Power control mode of DG

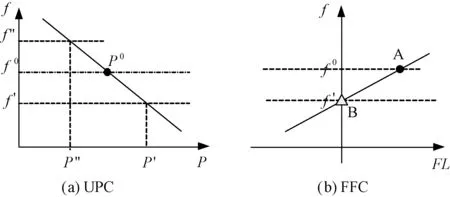
图2 UPC和FFC下垂特性曲线Fig.2 Droop characteristic in UPC and FFC mode

UPC控制与传统下垂控制相似，这种控制方式的目标是使DG的输出功率维持在一个恒定值。如图1(a)所示，为了达到这种控制目的，需要测量公共连接点的电压V和DG的输出电流I，通过测量的电压电流值计算出有功功率并反馈回控制器GC。这种控制方式中利用频率f作为各DG之间的公共信号来实现有功功率均分。有功功率和频率之间的关系为：

f=f0-KU(P-P0)

(1)

式中，KU为UPC控制模式的下垂系数；f0和P0分别为DG在给定工作点的频率和输出功率；f和P分别为DG在新的工作点的频率和输出功率。

根据UPC控制模式的特点，并网时无论负荷怎么变化，DG的输出功率都保持恒定不变，不足的功率由大电网补偿。孤岛运行时，失去了大电网的支撑，DG的输出功率就会跟随负载的变化而变化，如图2(a)所示，当负载增加时系统频率减小，从而使DG输出功率增加满足负荷需求，反之亦然。

FFC模式虽然也采用下垂控制，但是与传统下垂控制有很大不同。这种控制模式的特点是通过控制DG的输出功率，维持DG所在馈线上的潮流不变，即维持FLline恒定，如图1(b)所示，在这种控制模式中需要测量公共连接点处的电压V和电流Iline，计算出馈线潮流FLline，并反馈回GC。在FFC控制模式下，FL-f下垂特性曲线代替了P-f下垂特性曲线，馈线潮流和频率之间的关系为：

f=f0-KF(FL-FL0)

(2)

式中，KF为FFC模式下的下垂系数；f0和FL0为给定值；f和FL分别为新的工作点的频率和馈线潮流值。因为馈线潮流与DG输出功率之和等于负载功率，如式(3)所示，所以KF=-KU。

FLline+PDG=Pload

(3)

FFC控制模式的特点是，并网时如果负载增加，DG输出功率也会增加从而维持馈线潮流恒定，即无论负荷怎么变化，大电网向微电网馈送的潮流始终不变，因此微电网可以看作大电网的可控负载。孤岛时，大电网和微电网之间没有潮流交换，即馈线潮流为零，如图2(b)所示，系统工作点由A移动到B，只要DG输出功率不达到最大值，系统的频率都能维持恒定。

3 DG的连接方式与控制

在微电网中根据DG的连接方式不同可以分为串联结构和并联结构，再与DG的控制方式结合可以形成4种基本的微电网结构，如图3所示[14,15]。图3(a)和图3(b)中，串联级数越多时，对第n个DG来说，线路压降就越大，从而造成严重的无功环流；图3(d)的并联UPC结构中，与传统下垂控制相同，缺少FFC控制模式的DG来维持并网时馈线潮流恒定和孤岛运行时维持系统频率稳定，图3(c)中多个DG并联，脱网时造成频率偏差过大。因此本文采用了一种混合结构，如图4所示。这种结构综合了以上4种结构的特点，首先DG2和DG3并联，再与DG1串联，避免了多个DG同时串联时，由于存在线路压降，最后一个串联的DG连接点处的电压跌落大的问题，DG1采用FFC控制模式可以在并网时维持馈线潮流恒定，孤岛时维持系统频率稳定，不受负荷影响。

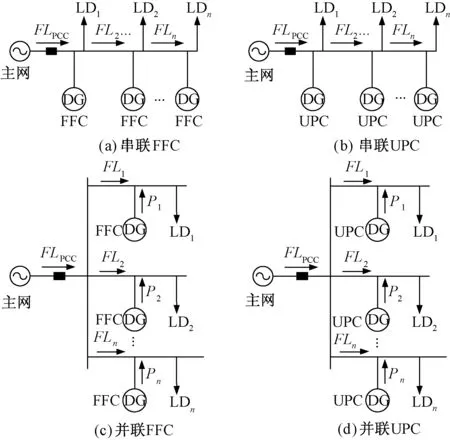
图3 微电网的不同结构Fig.3 Different configurations of microgrid

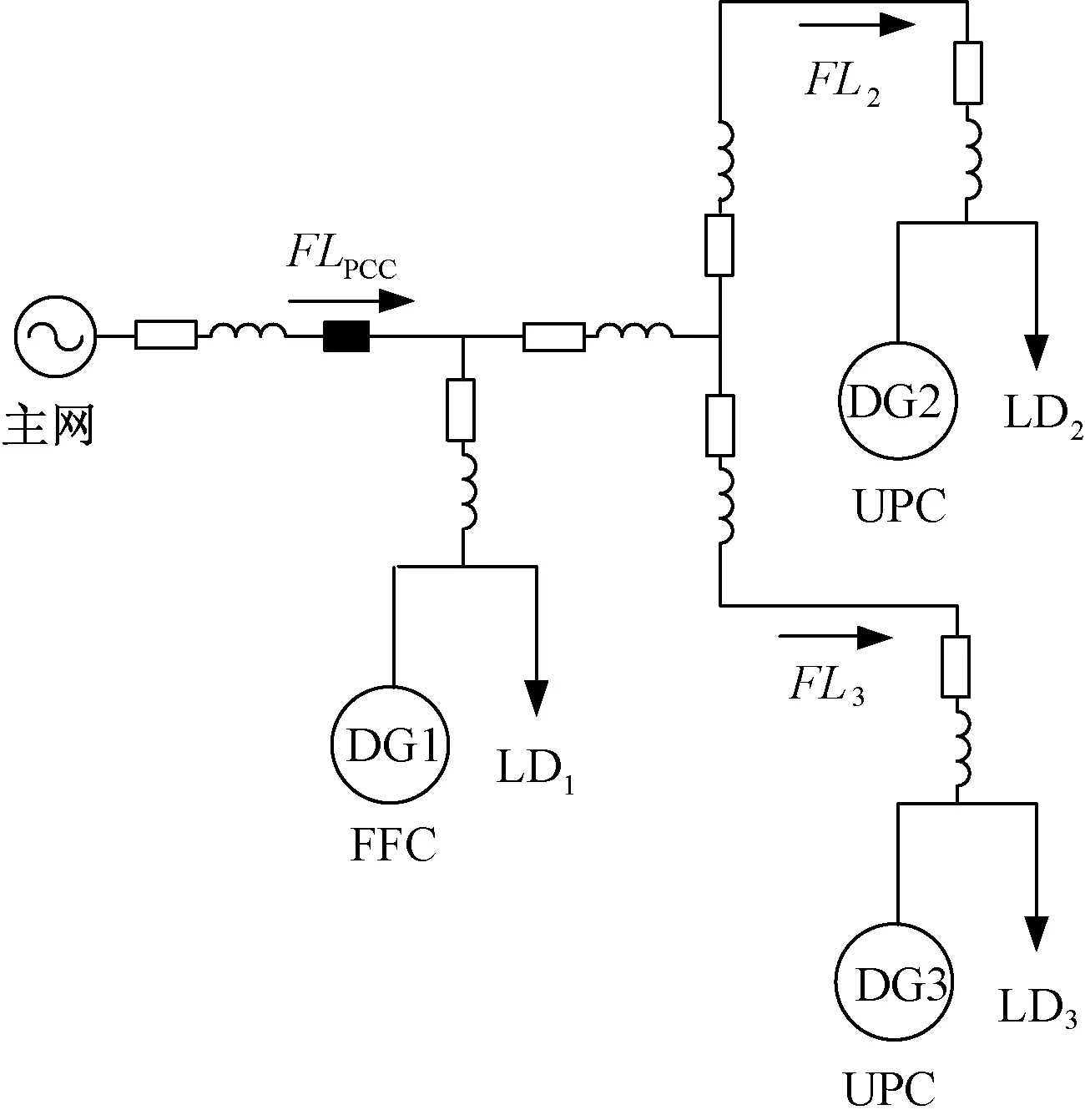
图4 带有3个DG的微电网Fig.4 Microgrid consisting of three DG units

4 功率均分控制策略

4.1 功率均分控制策略

R. H. Lasseter提出的FFC和UPC的分布式电源控制策略既可以工作在微电网并网模式，也可以工作在孤岛模式，并且在微电网工作模式切换时，无需改变分布式电源的控制策略。虽然FFC和UPC控制策略有其自身的优点，但是也存在不足，根据文献[8]，为了维持微电网并网时与大电网之间潮流的恒定，孤岛时微电网的频率不受负荷变化的影响，第一个与大电网连接的DG需采用FFC控制模式，当DG1采用FFC控制策略时，微电网中所有负荷的功率需求都要直接或间接地由DG1提供，这对DG1的功率要求很高，在峰值负荷时，DG1可能不足以提供这么大的功率。如果并网时增加大电网向微电网馈送的潮流，那么大电网可以补偿微电网中的一部分负荷，减轻对DG1的功率要求，但是馈线潮流又不能太大，这是因为如图2(b)所示，当微电网由并网向孤岛切换时，馈线潮流由给定值变为0，根据下垂关系可以得到：

Δf=f′-f0=KF1FLPCC

(4)

式中，Δf为微电网的频率偏差；f′为脱网后系统频率；f0为并网时系统频率；KF1为DG1的下垂系数；FLPCC为大电网向微电网输送的潮流。从式(4)可以看出，如果FLPCC过大，脱网后微电网的频率偏差Δf会超出系统的允许值，同时馈线潮流越大线路压降也越大。为了解决以上问题，提出了如下控制策略。

4.2 功率优化控制策略

本文以图4所示微电网结构为例进行分析，在图4中DG1采用FFC控制模式，DG2和DG3采用UPC控制模式，该控制策略适用于DG1采用FFC控制模式的微电网结构。

微电网并网运行时，从大电网的角度来看，希望无论负荷怎么变化微电网都可以视为大电网的可控负载，这就需要微电网和大电网之间的潮流交换恒定，对整个系统来说，大电网向微电网输送的功率、DG的输出功率和负荷之间满足如下关系：

(5)

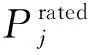
(6)

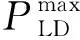
从式(6)可以看出，馈线潮流满足式(6)时，负荷处于峰值仍然能维持馈线潮流恒定。为了减小脱网时的频率偏差和并网时减小线路压降，馈线潮流应取式(6)的最小值，即

(7)

为了进一步减小线路压降、减小脱网时的频率偏差和缓解峰值负荷时对FFC控制模式的DG的功率要求，馈线潮流可以通过式(8)进一步减小，即当负载功率较大时，可以将UPC控制模式下DG的输出功率由额定值切换到最大值，这样也可以进一步减小FFC控制模式下DG的输出功率。

(8)

式(8)即为并网时馈线潮流所取的最小值。满足式(8)时，即使微电网中的负荷达到峰值，依然能够维持馈线潮流恒定，即微电网可以视为大电网的可控负载。同时馈线潮流可以取到最小值，减小了微电网脱网时系统的频率偏差和并网时的线路压降。因此在设计微电网时，根据DG的输出功率及其最大功率就可以得到馈线潮流的最小值。

当微电网孤岛运行时，微电网和大电网之间的潮流为零，则负载和DG的输出功率之间满足：

(9)

当微电网中的负载达到峰值时有：

(10)

为了减小峰值负荷时对FFC控制模式下DG的输出功率要求，即孤岛时减小FFC控制模式下DG的最大输出功率，那么只需要采取与上述并网时相同的控制策略，将UPC控制模式下DG的给定输出功率由额定值切换到最大值，如式(11)所示：

(11)

当Pj取最大值时，那么就可以进一步减小Pi的最大值，缓解峰值负荷时对FFC控制模式下DG的输出功率要求。以上是对本文所提出的控制策略的理论分析，下面介绍具体的控制过程。

以图4所示微电网结构为例。先讨论并网时的控制过程，DG1采用FFC控制策略，DG1的输出功率跟随负载变化而变化，DG2和DG3采用UPC控制策略，因此输出功率恒定，不随负载改变。当微电网中的负载增加时，DG2和DG3输出功率恒定，所以负载变化都要由DG1补偿，当DG1输出功率达到最大值时，为了使微电网和大电网之间的馈线潮流恒定，本文将采用式(8)和式(11)的控制策略，即改变DG2或DG3的功率给定值，将DG2或DG3的功率给定值由额定值切换到最大值。因为DG2和DG3是并联关系，所以可以根据两个DG的优先级切换工作模式，假设先切换DG2的输出功率给定值，其输出功率由额定值变为最大值，可以分担一部分负载变化，则DG1的输出功率就会减小。DG2输出功率给定值的切换条件为：

(12)

这时DG1工作在FFC控制模式，DG2工作在UPC控制模式，其输出功率给定值为最大值，DG3工作在UPC控制模式，其输出功率给定值为额定值。如果之后负载继续增加，DG2和DG3工作在恒功率状态，仍然由DG1增加输出功率补偿负载变化，当DG1再次达到最大输出功率时，将DG3的输出功率给定值由额定值切换到最大值，DG1的输出功率再次减小，DG3工作状态改变的条件为：

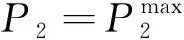
(13)

此时DG2和DG3都工作在最大输出功率状态，缓解了对DG1的功率要求。

当负荷减小时，需要将DG2和DG3的工作状态切换回额定值。当负载减小到一定值时，先将DG3的工作状态由最大输出功率切换回额定输出功率状态，切换条件为：

(14)

当负载继续减小时，需要将DG2的工作状态也由最大值切换回额定输出功率状态，切换条件为：

(15)

以上是并网时微电网的工作过程，当负载增加时本文以先改变DG2的工作状态为例进行分析。实际微电网运行过程中，应根据DG的优先级选择切换UPC控制模式下DG的工作状态，先切换优先级最高的DG的工作状态。而当DG输出功率由最大值切换回额定值时，应该先切换优先级最低的DG，这与负载增加时切换DG工作状态的顺序相反。

当微电网孤岛运行时，控制策略与并网运行时相同，通过切换UPC控制模式下DG的工作状态，可以使孤岛运行时微电网的频率不受负荷变化影响，从而维持微电网的稳定性。

5 仿真验证

5.1 微电网并网运行时的仿真结果

并网运行时微电网和大电网之间馈线潮流的给定值为FLPCC=2kW。负载的变化如图5所示，图6 (a)和图6(b)分别为与图5中负载变化相对应的传统功率控制策略和采用改进功率优化控制策略后的DG输出功率仿真结果。从图6(a)可以看出，随着图5中负荷的变化，DG2和DG3的输出功率维持恒定，在0.5s时，LD2达到峰值负荷，DG1输出功率达到极限值仍然不能满足负荷需求，因此大电网和微电网之间的馈线潮流变大不再维持恒定；0.5～2.0s时随着负载的不断增加，馈线潮流FLPCC随着负载的增加而变大，直到2.0s时，LD3退出峰值负荷。

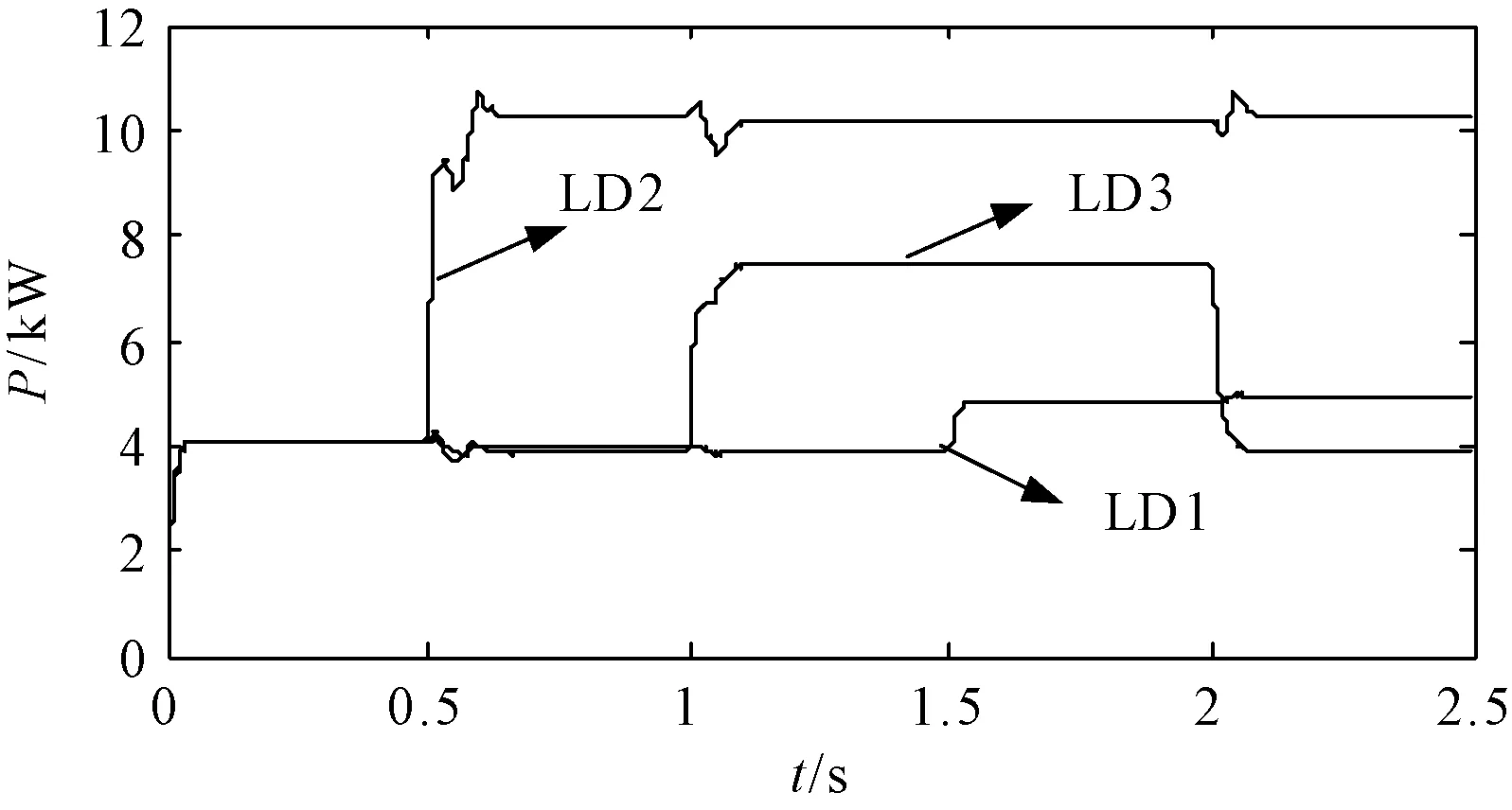
图5 并网时的负荷需求Fig.5 Load demands in microgrid

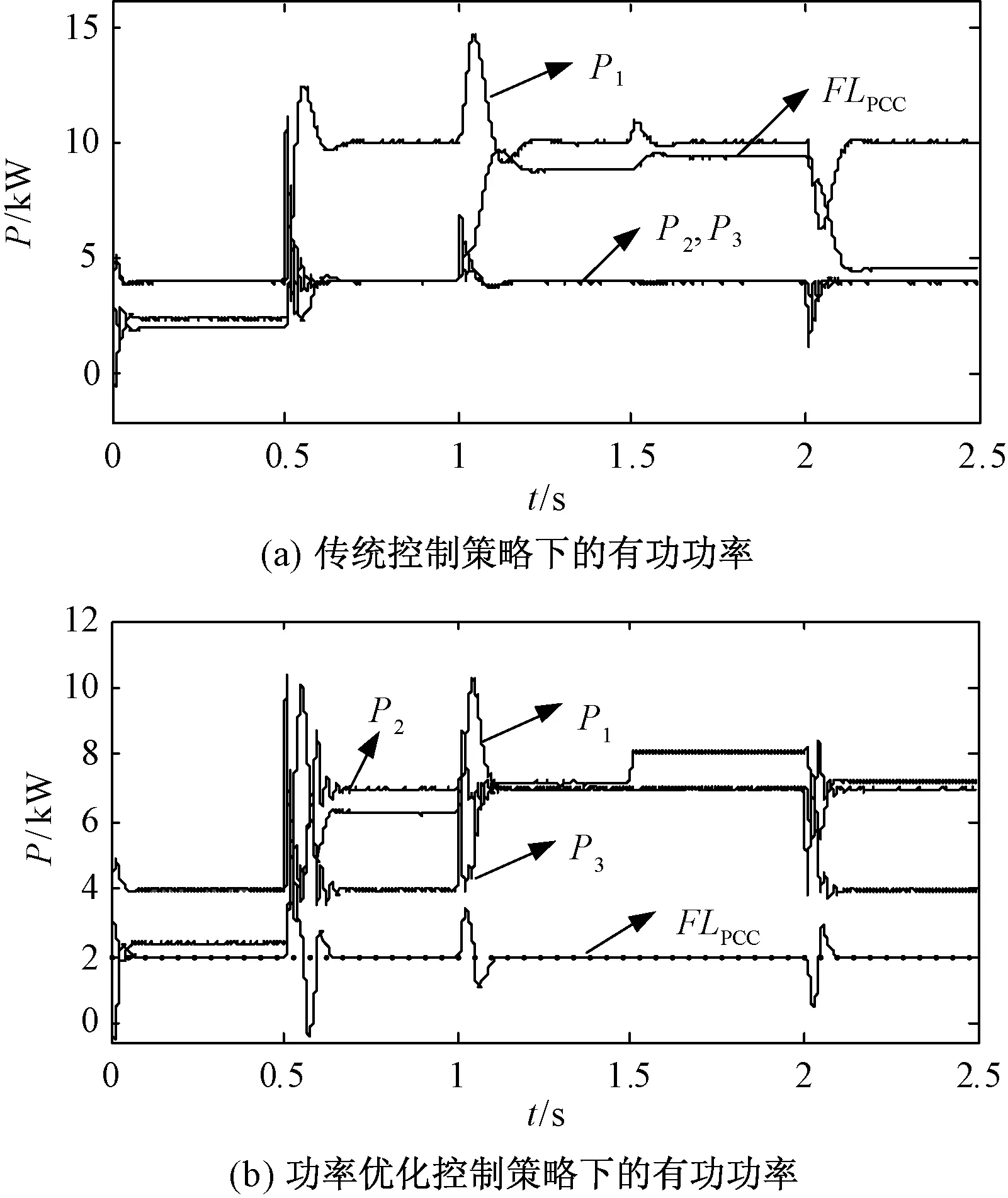
图6 并网时两种控制策略下的有功功率Fig.6 Active power of two control strategy in grid-connected mode

图6(b)中，0.5s时LD2增加使得DG1输出功率达到极限值，根据本文的控制策略，DG2的功率给定值从额定值切换到了最大输出功率，暂时缓解了对DG1的功率要求。1.0s时LD3又达到峰值负荷，DG1输出功率达到极限值仍不能满足负荷需求，将DG3的功率给定值也切换到最大值，以补偿负荷需求。1.5s时，LD1也达到峰值负荷，DG1输出功率增加，在这段时间内所有负荷都达到峰值。2.0s时LD3退出峰值，DG1能够满足剩余的功率需求，因此DG3切换回额定输出功率。图6(a)中，当DG1输出功率达到极限值时，馈线潮流随负载变化而变化，由大电网补偿不足的功率。而图6(b)中，在整个负载变化过程中，馈线潮流FLPCC始终维持恒定，只是在负载变化时出现短时扰动，因此可以将微电网视为大电网的可控负载，从而验证了本文提出的改进控制策略在并网时的正确性和可行性。

5.2 微电网脱网时的仿真结果

图7(a)和图7(b)分别为微电网脱网时传统控制策略和改进控制策略的仿真结果。0.9s时微电网脱离大电网，孤岛运行。根据式(4)可知，Δf与馈线潮流成正比，在一般控制策略下当DG1达到最大输出功率时，馈线潮流随着负载的增加而变大，那么脱网时Δf随馈线潮流变大而变大，脱网时频率偏差会随之变大。如图7(a)所示，Δf=1.4Hz，超出了系统允许的频率偏差值。

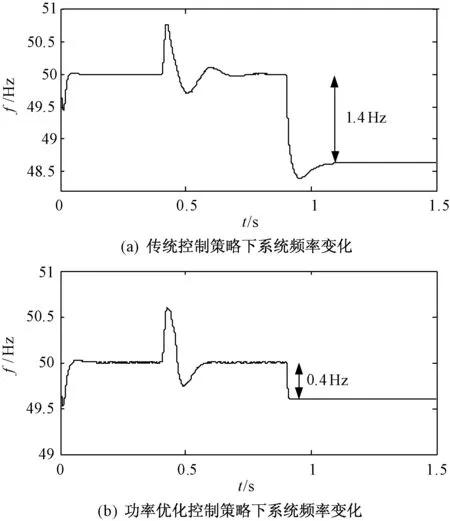
图7 微电网脱网时的系统频率Fig.7 Frequency of microgrid during transition mode

图7(b)为采用改进控制策略之后的系统频率。因为采用改进控制策略，所以负载变化不会影响馈线潮流，即馈线潮流在整个过程中都维持恒定，微电网可以视为大电网的可控负载。如图7(b)所示，虽然0.4s时负载增加，但是不影响FLPCC，脱网时系统频率偏差只有0.4Hz，满足系统的要求。

5.3 微电网孤岛运行时的仿真结果

微电网孤岛运行时，微电网和大电网间没有潮流交换，即FLPCC=0。孤岛运行时希望系统频率不受负荷变化影响，下面仿真结果验证了所提方案的有效性。图8为微电网孤岛运行时负载变化情况。

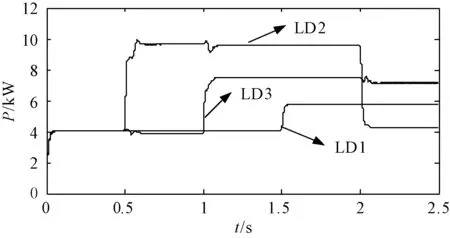
图8 孤岛时的负载需求Fig.8 Load demands in islanded mode

图9 (a)和图9(b)分别为微电网孤岛运行时，采用传统控制策略和改进控制策略的DG的输出功率仿真结果。图9(a)中，0.5s时LD2达到峰值负荷，DG1输出功率达到极限值，仍不能满足负荷需求，所以在传统控制策略下微电网应该按照P-f下垂特性使系统频率减小，从而增加DG2和DG3的输出功率。图10为孤岛时微电网频率的仿真结果。如图10(a)所示，在0.5s时系统频率降低，此时DG2和DG3的输出功率都增加，以补偿剩余的负荷，如图9(a)所示。在1.0s和1.5s时LD3和LD1分别达到峰值负荷，所以系统频率继续减小，使DG2和DG3的输出功率增加以满足所需的负荷。2.0s时负载减小，DG1的输出功率能够满足负载需求，因此系统频率恢复到50Hz，DG2和DG3的输出功率也恢复到额定值。

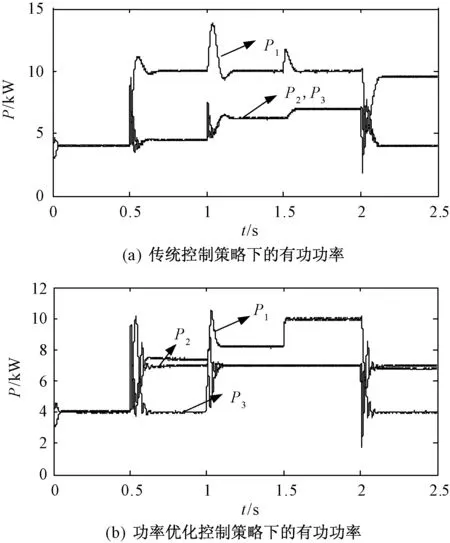
图9 孤岛时逆变器输出有功功率Fig.9 DG output active power in islanded mode

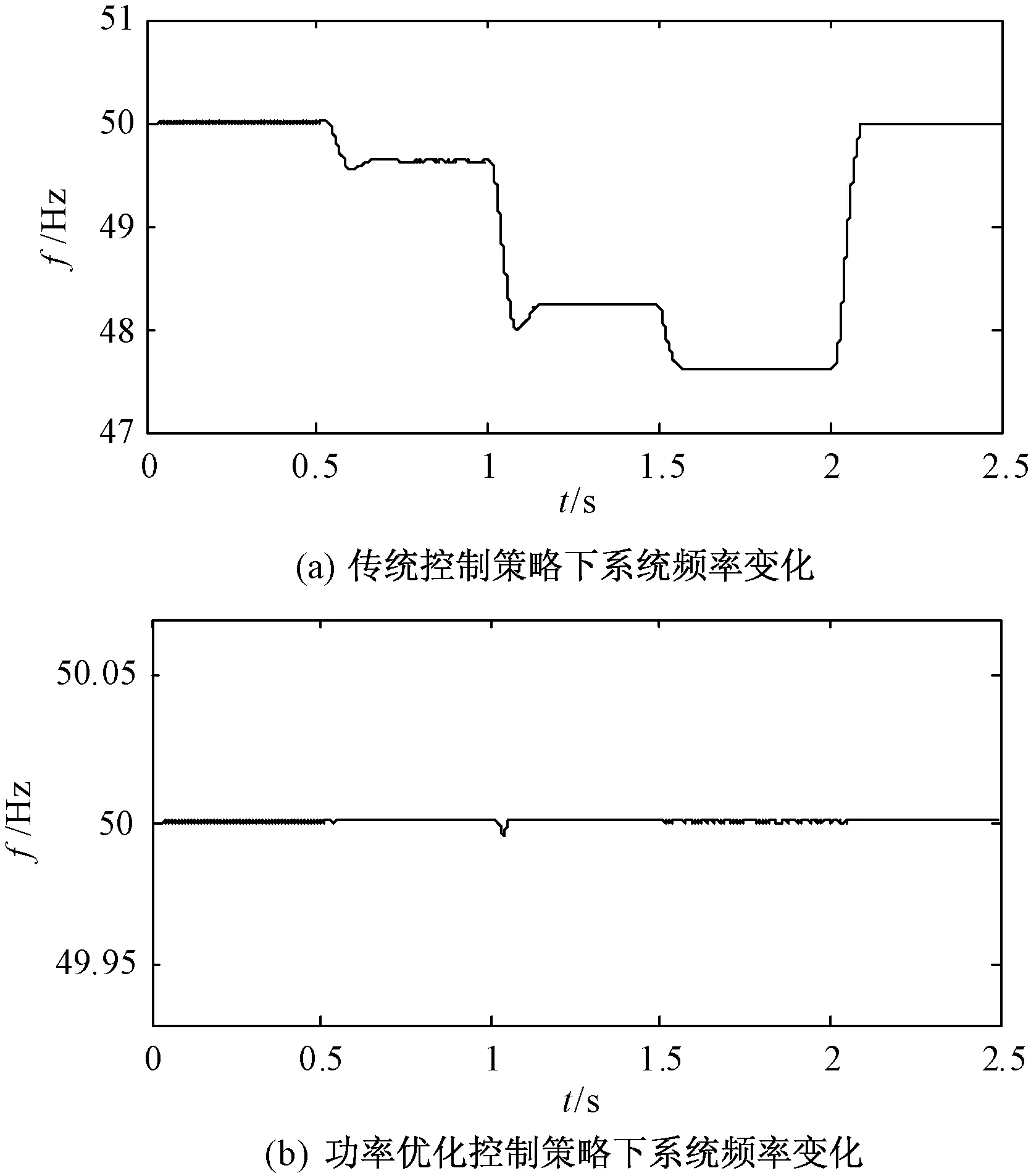
图10 孤岛时微电网频率Fig.10 Microgrid frequency in islanded mode

从图9(a)和图10(a)可以看出，孤岛运行时在传统控制策略下，当DG1输出功率达到最大值后，随着负载不断增加，系统频率随之减小，这不利于负载和微电网的稳定运行。

从图9(b)和图10(b)可以看出，0.5s时负荷增加后，DG1输出功率达到最大值，因此DG2的输出功率由额定值切换到最大值，暂时缓解了对DG1的功率要求，1.0s时LD3达到峰值负荷，DG3的输出功率由额定值切换到最大值，以补偿负荷变化。整个过程中DG1的输出功率都没有达到极限值，因此系统频率始终维持恒定。

通过孤岛模式的仿真结果可以看出，在传统控制策略下，当DG1输出功率达到极限值后，系统频率随负载不断变化，不利于微电网和负载的稳定运行；而采用改进控制策略之后，当DG1输出功率达到极限值时，改变DG2和DG3的输出功率可以减小DG1的输出功率，从而使系统频率维持恒定，不随负载变化，微电网和负载能够稳定工作。

6 实验验证

本文以两台逆变器串联为例验证孤岛时有功功率协调控制策略的有效性，实验中第一台逆变器采用FFC控制模式，第二台逆变器采用UPC控制模式，分别验证未采用有功功率协调控制的实验波形和采用有功功率协调的实验波形。实验参数如下：直流侧输入电压200V，DG1本地负载34Ω，DG2本地负载65Ω，因为模拟微电网孤岛运行所以DG1馈线潮流给定值为零，DG2有功功率给定值为110W，DG1输出功率最大值设为300W，DG2有功功率最大值为310W，实验中突加负载的有功功率为ΔP=220W。

图11为传统控制策略下的实验波形。可以看出，突加负载之前DG2跟随参考功率输出，不足的负载功率由DG1补偿，突加负载时DG1输出达到最大值时其输出功率维持不变，不足的功率由DG2补偿，如图11 (a)所示。这种控制策略的缺点是DG2输出功率的变化会引起系统频率的改变，如图11 (b)所示，系统频率下降了0.3Hz。当系统所缺功率值较大时会造成频率下降过大，造成系统不稳定运行。

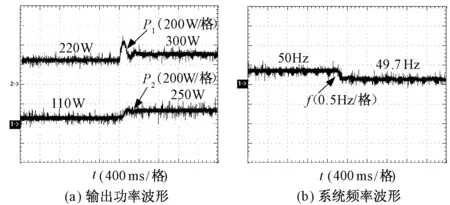
图11 传统控制策略下的实验波形Fig.11 Experimental waveforms under traditional control strategy

图12为功率优化控制策略下的实验波形。可以看出，突加负载之前各DG输出功率和传统控制策略相同，当突加负载时，因为DG1采用FFC控制，所以负载增加值由DG1补偿，当DG1输出功率达到最大值时，加入有功功率协调控制将DG2的输出功率由额定值切换到最大值，从而缓解DG1的功率压力，计算可得到DG1输出功率为240W，低于其最大输出功率，从而可以保证系统频率不变。对比图11和图12可以看出，采用本文所提出的控制策略可以实现孤岛时系统频率始终保持50Hz不变。

图12 功率优化控制策略下的实验波形Fig.12 Experimental waveforms of power optimization control strategy

7 结论

采用改进的控制策略，并网运行时可以使微电网和大电网之间的馈线潮流维持恒定，微电网可以视为大电网的可控负载；采用改进控制策略后馈线潮流不随负载变化，微电网脱网时系统频率跌落小，频率敏感负载能够稳定工作；孤岛运行时，采用改进控制策略DG1输出功率不会达到最大值，系统频率能够维持恒定，不受负载影响，微电网能够更稳定地运行。

参考文献(References)：

[1] 杨新法，苏剑，吕志鹏，等(Yang Xinfa, Su Jian, Lv Zhipeng, et al.).微电网技术综述(Overview on micro-grid technology)[J].中国电机工程学报(Proceedings of the CSEE)，2014，34(1)：57-70.

[2] 朱永强，贾利虎，王银顺，等(Zhu Yongqiang, Jia Lihu, Wang Yinshun, et al.).微电网结构设计的基本原则(Basic design principles for micro-grid architecture)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(9)：44-63．

[3] Lasseter R H. Microgrids [A]. 2002 IEEE Power Engineering Society Winter Meeting [C]. 2002. 305-308.

[4] Piagi P, Lasseter R H. Autonomous control of microgrids [A]. 2006 IEEE Power Engineering Society General Meeting [C]. 2006.1-8.

[5] 谢永流，程志江，李永东，等(Xie Yongliu, Cheng Zhijiang, Li Yongdong, et al.).引入虚拟阻抗的并联逆变器新型下垂控制策略 (New droop control strategy for parallel inverter with virtual impedance)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(3)：23-61．

[6] 姚玮，陈敏，牟善科，等(Yao Wei, Chen Min, Mou Shanke, et al.).基于改进下垂法的微电网逆变器并联控制技术(Paralleling control technique of microgrid inverters based on improved droop method)[J].电力系统自动化(Automation of Electric Power Systems)，2009，33(6)：77-80．

[7] Majumder R, Ghosh A, Ledwich G, et al. Power management and power flow control with back-to-back converters in a utility connected microgrid[J]. IEEE Transactions on Power Systems, 2010, 25(2): 821-834.

[8] Nguyen K L, Won D J, Ahn S J, et al. Power sharing method for a grid connected microgrid with multiple distributed generators[J]. Journal of Electrical Engineering & Technology, 2012, 7(4): 459-467.

[9] Loc N K, Jin D G, Won D J. A study on active power and frequency response in microgrid [A]. 2011 IEEE Trondheim PowerTech [C]. 2011. 1-6.

[10] Ahn S J, Park J W, Chung I Y, et al. Power-sharing method of multiple distributed generators considering control modes and configurations of a microgrid[J]. IEEE Transactions on Power Delivery, 2010, 25(3): 2007-2016.

[11] Katiraei F, Iravani M R. Power management strategies for a microgrid with multiple distributed generation units[J]. IEEE Transactions on Power Systems, 2006, 21(4): 1821-1831.

[12] Al-Saedi W, Lachowicz S W, Habibi D, et al. Power flow control in grid-connected microgrid operation using particle swarm optimization under variable load conditions[J]. International Journal of Electrical Power & Energy Systems, 2013, 49: 76-85.

[13] Raghami A, Hamzeh M, Ameli M. Optimal power management in a microgrid with multiple electronically interfaced DG units [A]. The 5th Annual International Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014) [C]. 2014. 90-95.

[14] Ahn S J, Nam S R, Choi J H, et al. Power scheduling of distributed generators for economic and stable operation of a microgrid[J]. IEEE Transactions on Smart Grid, 2013, 4(1): 398-405.

[15] Haddadi A, Joos G. Load sharing of autonomous distribution-level microgrids [A]. 2011 IEEE Power and Energy Society General Meeting [C]. 2011. 1-9.