某博览城轨交枢纽中大跨度钢楼梯的人致振动分析

朱枫，张 瑶

（1.广州地铁设计研究院有限公司,广东 广州 510010；2.悉地（苏州）勘察设计顾问有限公司,江苏 苏州 215000）

0 引言

人致荷载引起结构振动的问题由来已久，从19世纪初德国萨勒河一座78 m悬索桥的倒塌，到2000年英国千禧桥开通3 d即因过量的横向振动而关闭，至此在世界范围内引起了对桥梁人致振动问题的研究。除了桥梁领域，人致振动在大跨度楼盖、长悬臂结构、体育看台、大跨度楼梯等柔性结构中同样存在。产生上述人致振动的荷载即为人致荷载，人致荷载主要包括人在步行、跳跃、奔跑、起立、有节奏的律动等动作时对结构产生的动力荷载，通常具有周期性。

近年来，随着交通枢纽项目和大型公共场所这些建筑功能的复杂化，加之建筑师对美学的追求，楼梯在其中除担任着人流导向和消防疏散的重要功能之外，其造型也向着大跨度和纤细化的方向发展。目前对于楼梯上行人的脚步荷载和同步性等问题研究较少，因此对人致楼梯振动问题应引起重视。

1 楼梯人行荷载

1.1 平地步行的单人脚步荷载

人在平地上正常行走的频率在2 Hz左右。Andriacchi等[1]利用测力板方法测量了单人脚步荷载在3个方向上的分量，其竖向分量时程曲线如图1（a）所示。由图1（a）可见，该竖向分量有2个波峰和1个波谷，2个波峰对应脚落地和离开地面2个时刻。图1（b）为连续行走的脚步荷载时程曲线，由图中可注意到步行时有一段双脚同时落地的重叠曲线。

图1 平地脚步荷载时程曲线

1.2 行人在楼梯上行走的脚步荷载

与人在平地上的行走过程不同，人在楼梯上的行走动作分为上行和下行两种情况,直观的感受是上楼梯费力下楼梯轻松。上楼时行人首先用脚掌接触台阶，向下用力使重心抬高，然后当该脚将抬起时脚跟短暂着地，并利用脚尖推动向上。下楼时行人首先顺势用脚掌接触台阶，当再次利用脚尖抬起向下之前脚跟短暂着地。

Bishop[2]利用测力板按不同的行走速率，得到了大量的脚步荷载曲线，图2为楼梯上下行脚步荷载的时程曲线。由图2可见，上行楼梯速率较平地步行慢，荷载峰值略高，时程曲线波谷较平缓。

图2 楼梯上下行脚步荷载时程曲线

杜永峰等[3]利用固定在人体质心位置的MEMS加速度传感器获得900组连续的荷载时程数据，与Bishop的研究成果具有很好的一致性，并指出下楼梯时的人行荷载更容易引发结构的相应振动。

以上研究结果均表明上下楼梯时的脚步荷载时程曲线有以下特点：

（1）脚步荷载峰值随着步频的加快呈增大趋势。（2）上下楼梯的荷载峰值高于平地步行状态。（3）下楼脚步频率通常高于上楼脚步频率，下行荷载峰值明显大于上行荷载峰值。

1.3 行人上下楼梯的行为特征

（1）在轨道交通车站中，楼梯作为重要的垂直运输设施，处于咽喉地位，由于具有一定的坡度，行走的平顺性和稳定性较平地差，行人速度相对平地慢。

（2）考虑轨道交通中楼扶梯设置特点，上行通常设置扶梯，楼梯更多为考虑下行使用。

（3）由于楼梯自身结构特性，台阶具有固定模数，行走时每一步的距离为同样模数。

（4）出站口的楼梯处，随列车到发客流具有波动性[4]。

（5）当人流量少时，对时间价值较高的行人，存在一步2～3阶上楼梯的情况，亦有小跑下楼梯的行为，甚至以跳跃的方式下楼；通常行人可按自己的期望速度上下楼梯而不受其他人的干扰。

（6）当人流量逐渐增多，人群密度增大时，行人迫于后方的压力或是为了追随前方行人步伐，速度会有明显提高[5]。

（7）轨道交通枢纽的人流量大，人群密集，极易产生拥堵现象，受限于楼梯宽度和台阶模数，个体和群体的速度差异变小，人群以行人流体特征呈现，整体通行速度下降，脚步速率趋于一致，表现出群体行为[6]。

（8）当楼梯上行人发现列车即将进站信息时，为避免错过班车，会主动加快脚步。

（9）不同时间段的行人速度存在差别，早高峰因为急着上班打卡，行人平均速度较晚高峰和平峰时段高。

基于行人在楼梯上行走产生的荷载时程曲线较平地行走时存在较大差异，以及行人在楼梯通行过程中的特性，尤其是交通枢纽中可能产生的人群密集、同步性等情况，极有可能对大跨度楼梯产生过大的激振，因此有必要做针对性的研究。另外相比平地行人荷载，楼梯上下行时的脚步荷载、主要频率范围等也存在差异，使得楼梯振动敏感频率范围加大，分析的工况将成倍增加。

2 脚步荷载模型

2.1 单人脚步荷载模型

参照Bachmann等[7]的研究，任一典型动作如行走、跑、跳、舞蹈、鼓掌等基于人体周期性的动作，所产生的动力荷载在数学上均可采用傅里叶级数的形式表达。故单人在楼梯上行走的连续脚步荷载采用如下表达式：

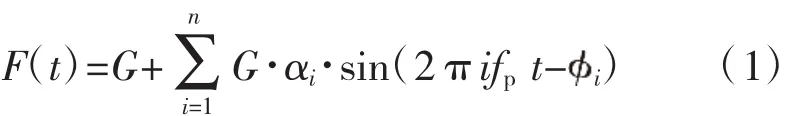
式中：F（t）为动力荷载时程；G为体重，可按0.7 kN计；t为时间；fp为行人在楼梯上的运动频率；αi为第i阶动载因子，为谐波幅值与体重G的比值，其数值见表1[8]；i为第i阶谐波相位角。

2.2 多人脚步荷载模型

多人荷载不仅存在行人与行人之间的相关性，还存在行人与结构之间相互作用的问题[9]。当人数较多时，对结构的阻尼、频率等产生的影响较大，不可忽略。目前对于多人荷载数学模型的研究尚未有普遍认可的成果，其核心是如何描述人群中个体间的协同性，即人群中个体之间保持同步的程度问题。

在研究多人脚步荷载时，采用“组”和“群”的概念[10]。“组”指5人左右的行人结伴成组，按同一方向和相近的速度行走，“群”指均匀分布于结构面的全体行人。按这一原则，可初步将多人荷载划分为以下4种类型：

表1 楼梯脚步荷载的谐波动载因子[8]

（1）小组结伴而行；

（2）低密度人群自由行走；

（3）高密度人群流动；

（4）横向动力失稳的“锁定”状态。

前3种类型可以评估不失稳条件下振动的最大加速度；第4种类型可以判断引发动力失稳的临界人数，但不在本文讨论范围之内。

2.2.1 小组结伴而行

行人的步频fp、步长lp和速度vp间存在下列关系：

因此，1组人结伴而行时，他们每个人的速度vp几乎相等，加之他们在楼梯上行走，每一步的步长相等，所以步频也相近，大部分人会进入同步状态（相位相同）。有研究者认为，1阶谐波分量很容易实现同步，2、3阶谐波同步的可能性就小很多，因此，对于小组结伴而行的动力荷载时程可以采用单人脚步荷载的1阶谐波分量乘以小组人数n来估算：

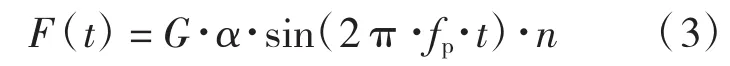
2.2.2 低密度人群自由行走

当人群密度较低时（小于0.5人/m2），个体间行走不受影响。根据随机振动理论，Matsumoto提出n个幅值相等但相位随机分布的输入所产生的线性结构的动力响应，正好是单个输入响应的

法国交通部出版的《人行桥技术指南》（以下简称为“法国指南”）进一步假定步频服从高斯分布，相位在0～2π之间均匀分布。等效行人数Np计算公式为：

式中：ξi为阻尼比。

2.2.3 高密度人群流动

当人群拥挤时，同步的可能性非常大，“法国指南”针对此种情况，同样通过随机振动原理，给出高密度人群下的等效行人数Np计算公式：

因为受台阶宽度限制，每步距离0.3 m，频率fp=3.82 Hz，可以得出vp=1.15 m/s。按节点顺序逐一输入时程荷载和荷载作用的起始时间，可以计算得到钢楼梯的动力响应。

3 工程实例

3.1 工程概况

某博览城交通枢纽工程中的1组钢楼梯和电扶梯连接地下车站站厅层与高架桥面，出于建筑效果，不设中间支墩，其中钢楼梯跨度为33.725 m，宽1.8 m，采用管桁架形式，其示意图见图3。

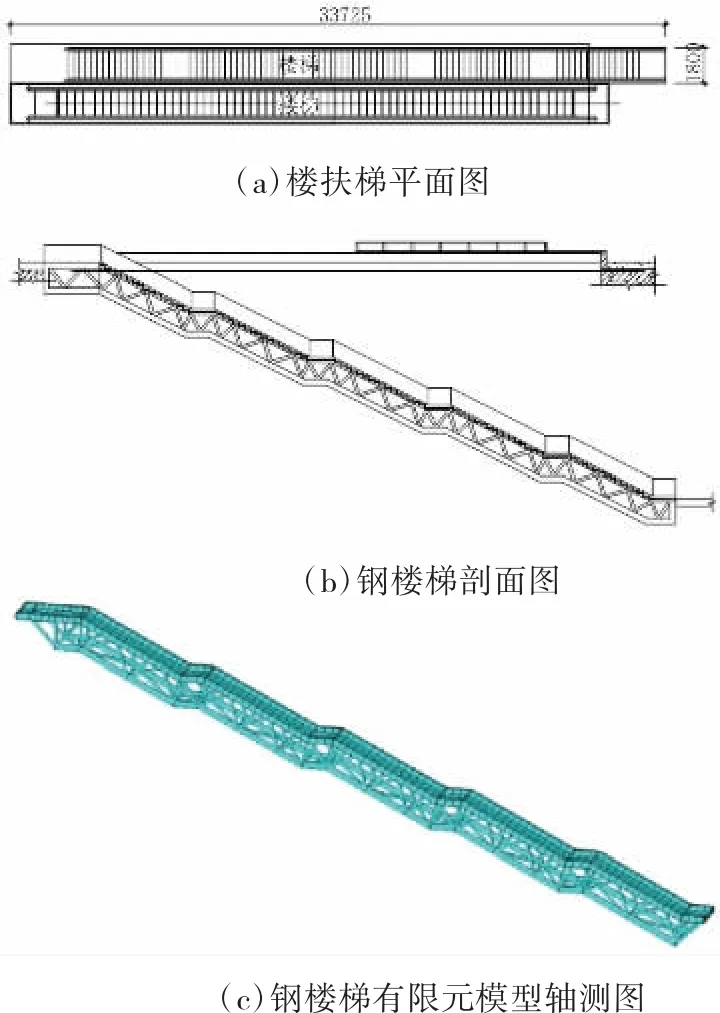
图3 钢楼梯示意图（单位:mm）

3.2 自振频率及敏感性分析

经分析，钢楼梯第一振型为竖向振动，频率f1=1.571 3 Hz；第二振型为横向振动，频率f2=2.171 5 Hz；第三振型为扭转振动，频率f3=5.213 0 Hz。

根据德国标准（DIN 4150-2-1999）的敏感频率范围评价准则，竖向振动的敏感频率范围为1.6～2.4 Hz，横向振动的敏感频率范围为0.5～1.2 Hz。本工程钢楼梯第一振型位于竖向敏感频率范围的边界，因此需对钢楼梯进行人群荷载作用下的舒适度分析，验算结构的竖向加速度响应是否满足相关规范[11-12]的要求；横向振动因远离敏感频率范围，本文不考虑在人群横向荷载作用下的振动问题。

3.3 人行荷载工况分析

本案例中只布置一扶一楼。考虑少量情况会有从楼梯上行的人员，因此本文仅分析行人下楼梯的情况，取2.2节分析的3种人群工况，另加单人跑步下楼工况共4种人行荷载工况。

（1）小组结伴而行：人数取5人，按正常速度自上而下通过楼梯计算，结构的竖向最大加速度为0.23 m/s2。图4为小组人群荷载下结构的加速度响应。

图4 小组人群荷载下结构的加速度响应

（2）低密度人群按小于0.5人/m2计，取总人数为30人，Np=6人，按正常速度的行人流进行计算。按行人流计算时，Np沿楼梯长度方向均匀分布，平稳段结构的竖向最大加速度为0.16 m/s2。图5为低密度人群荷载下结构的加速度响应（平稳段）。

（3）高密度人群：楼梯宽1.8 m，按3股人流计算，又假定每排行人间间隔1个台阶，n=170人,人群密度为 2.8人/m2，Np=1布于楼梯，按中慢速行人流进行模拟分析，结构的竖向最大加速度为1.2 m/s2。图6为高密度人群荷载下结构的加速度响应。

图5 低密度人群荷载下结构的加速度响应（平稳段）

图6 高密度人群荷载下结构的加速度响应

（4）小跑下楼：因为受台阶宽度限制，每步距离 0.3 m，频率 fp=3.82 Hz，可以得出 vp=1.15 m/s，按节点顺序逐一输入时程荷载和荷载作用的起始时间，计算得出最大加速度为0.06 m/s2。图7为单人小跑荷载下结构的加速度响应。

从以上4种工况可以看出，工况3高密度人群荷载激振下的结构加速度响应最大，达到1.2 m/s2。按同样的人流密度，采用平地状态下的脚步荷载进行比较，得到结构的竖向最大加速度为0.2 m/s2，如图8所示。

显而易见，按平地脚步荷载计算的结构加速度响应远小于以楼梯脚步荷载计算的结果，表明选取合适的脚步荷载模型对楼梯结构的人行致振分析至关重要。

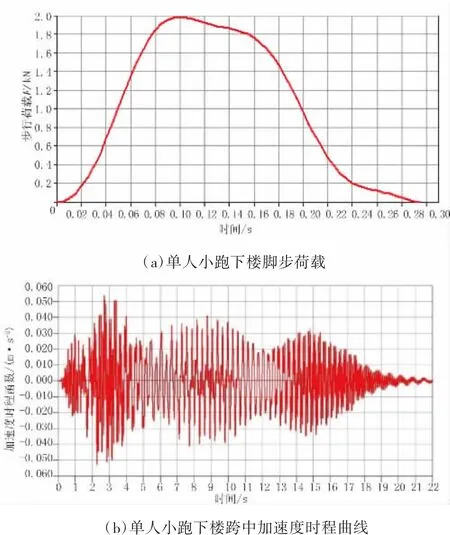
图7 单人小跑荷载下结构的加速度响应

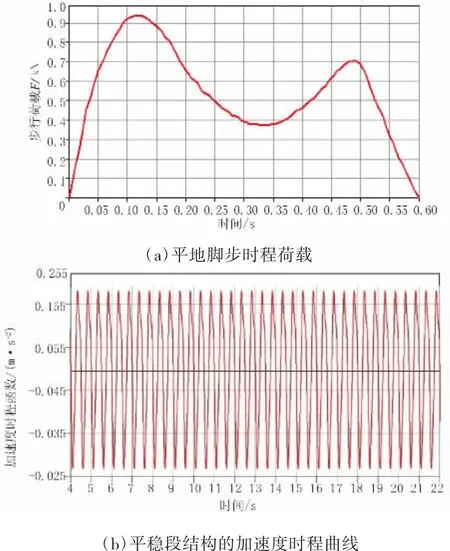
图8 高密度人群荷载下结构的加速度响应（取平地人行荷载）

鉴于楼梯自身结构形式的特殊性，人群拥挤情况下极易产生同步现象，因此应进一步研究密集人群状态下行人脚步的同步率问题。此时人-结构的相互影响不容忽视[13]，应考虑人体对结构阻尼、自振频率等的影响。

本工程运用调谐质量阻尼器（TMD）对楼梯进行减振，同时采取现场振动测试的方法对楼梯舒适度作了精确评价，并与本文模拟结果进行了对比分析。

4 结论

（1）通过比较平地人行脚步荷载和楼梯上下行脚步荷载的特性，初步判定大跨度楼梯的人行致振分析中应按行人的楼梯脚步考虑。

（2）根据单人脚步荷载建立多种人群荷载模型，并结合工程实例进行模拟，得出高密度人群下的结构响应最大加速度达到1.2 m/s2，远大于按平地人行荷载计算的结果。

（3）对大跨度钢结构楼梯的舒适性设计应引起充分重视，如计算不满足舒适度标准的情况，建议采用调谐质量阻尼器（TMD）作为减振措施。

[1]Andriacchi T P,Ogle J A,Galante J O.Walking speed as a basis for normal and abnormal gait measurement[J].Journal of Biomechanics,1977,10:261-268.

[2]Bishop N.Human induced loading of flexible staircases[J].Safety Science,1995（18）:261-276.

[3]杜永峰，刘路路，朱前坤,等.上下楼梯时人行荷载模型参数的试验研究[J].振动与冲击，2016，35（21）:220-228.

[4]袁振洲.城市轨道交通枢纽楼梯通行能力计算与仿真[D]北京：北京交通大学，2015.

[5]常丹.地铁行人微观行为参数量化研究[D].北京：北京交通大学，2010.

[6]王洪臣，张宁，何铁军.地铁车站行人交通的微观特性[J].城市轨道交通研究，2013，16（12）：74-79.

[7]Bachmann H，Prelove A，Rainer H.Vibration problem in structures:Practical guidelines[S].Basel：Birkhauser Verlag,1995.

[8]Kerr S.Human induced loading on staircases[D].London:University of London,1998.

[9]陈隽.人致荷载研究综述［J］.振动与冲击，2017,36(23）:1-9.

[10]陈政清,华旭刚.人行桥的振动与动力设计［M］.北京：人民交通出版社，2009.

[11]Steel design guide series 11:Floor vibrations due to human activity[S].[S.l]:American Institute of Steel Construction,2003.

[12]黄健，王庆扬，娄宇.基于国内外不同标准的人行天桥舒适度设计研究[J].建筑结构，2008(8）:106-110.

[13]陈舟.大跨度柔性人行桥人致非线性振动研究[D].广州：华南理工大学，2015.