基于组合预测模型的物流园区货运量预测研究

张九跃，张顺英

（山东天为工程技术有限公司，山东 淄博 255000）

0 引言

货运量预测是指根据国家或地方的统计部门发布的历史数据，研究分析某一时期的数据变化规律，建立预测模型，运用定性和定量分析方法，对货物运输量的未来变化进行预测。货运量预测是物流系统规划、物流资源合理配置过程中的重要环节，同时也是政府部门制定物流产业发展规划与政策的基础工作，准确预测货运量具有非常重要的意义。货运量预测方法一般分为两类，即定量方法和定性方法。由于定性方法主观影响因素太多，方法很难标准化，准确性很难把握，所以在实践中应用较多的是定量方法。目前，研究的定量方法多达100多种，常用的主要有指数平滑、灰色系统、回归模型、神经网络等。如W.Babcoock、Xiao Hulau等分别将回归预测和时间序列预测进行对比，采用时间序列模型进行实证研究，对铁路谷物进行货运量预测，并取得较好的结果[1]。Gregory A.Godfrey等对于指数平滑和ARIMA预测方法的比较研究，认为指数平滑预测在实际操作运用上更为容易，且指数平滑预测的误差也比ARIMA预测低[2]。Paulo S.A.Freitas 和 Antnioj.L.Rodrigues 讨 论了神经网络预测模型的联合预测方法，他们在模型方法中考虑了高斯径向函数网络，从不同模型中拓展了常用的线性联合估计模型的框架。黄荣富、张云康等都研究了指数平滑预测方法在物流需求上的运用，且辅以组合预测和实证对比分析[3-4]。柴大胜、潘英英等分别将灰色模型应用在物流园区、物流中心、公路物流的货运需求预测[5-6]。但是如果只选择其中一种方法进行物流需求预测，通常会存在一定的局限性，不能很好地体现每种方法的预测优势，因此提出一个具有通用性、能够将多种预测方法综合集成的组合预测方法是十分必要的。故本文运用弹性系数法、灰色模型法、三次指数平滑法的组合预测模型，来克服单一预测方法的局限性，尽可能提高预测的精度，并以某物流园区进行实例计算。

1 组合预测模型构建

1.1 弹性系数法

“弹性”一词来源于材料力学中的弹性形变概念，现在被广泛应用于很多领域。在公路工程建设中，所谓的运输弹性是指运输的生产弹性，通过研究运输弹性，从总体上把握未来交通运输的发展趋势。弹性系数法的数学模型为：

式中：yt为交通量在时刻t的预测值；为交通量在当前时刻t的值；i′为交通量在过去一段时间的平均增长率，%；i为交通量在今后一段时间的平均增长率，%；q′为类比变量在过去一段时间的平均增长率，%；q为类比变量在今后一段时间的平均增长率，%。

通常，经济增长促进交通运输业发展；然而当经济快速发展时，交通运输业又会成为其制约因素。可见，交通运输业的发展与国民经济增长密切相关。在交通量预测中，由于交通运输指标与经济指标具有较大的相关性，一般选用交通量的增长率与国民经济增长率的比例关系作为弹性系数，用以衡量运输变动对经济变动的反应程度：

1.2 GM模型即灰色模型（GREYMODEL）

通过对原始数据进行生成来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测系统未来的发展趋势。灰色系统理论认为，对既含有已知信息又含有未知或非确定信息的系统进行预测，就是对在一定方位内变化的、与时间有关的灰色过程的预测。尽管过程中所显示的现象是随机的、杂乱无章的，但毕竟是有序的、有界的，因此这一数据集合具备潜在的规律，灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。

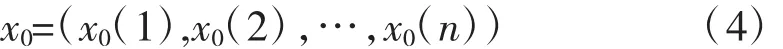
首先，构造货运量的初始时间序列：这里表示连续年的货运量，为削弱时间序列的随机性使规律性更加明显，采用一次累加，得到弱随机序列，所用公式如下：式中：a、b为待定参数，可用最小二乘法求得（a称为发展系数，b称为灰色作用变量）。

其次，对数据累加后的数列用线性动态模型来模拟和逼近，建立一阶灰色微分方程 GM（1，1）预测模型：

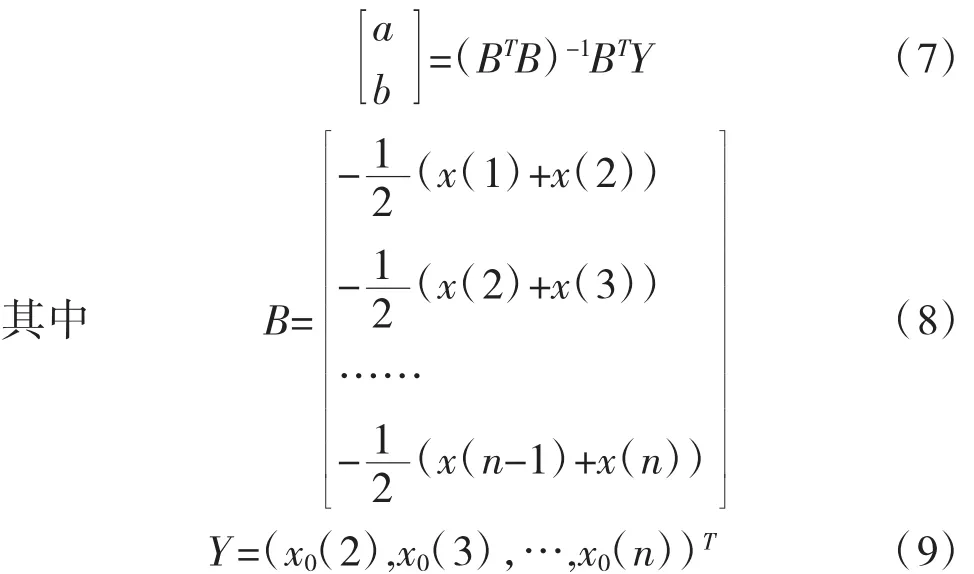
将式（7）求得参数代入式（6），得到所要建立的灰色微分方程，然后求解该方程，方程的解即需要的预测模型，称之为时间响应函数：

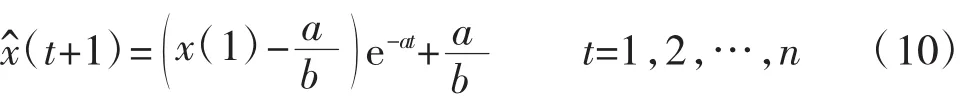
最后由于灰色系统理论建立的是累加数据的模型，因此我们必须对累加的数据进行还原，得到还原模型：

G

M（1，1）模型的综合预测公式为

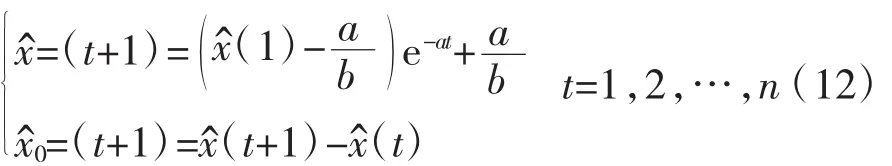
式中：t为年份，x（t）为要求年的货运量。

1.3 三次指数平滑法

指数平滑法将反映历史变化情况的统计数据，加以大致修匀平滑，以便分析变量的演变趋势。指数平滑法作为一种典型的时间序列预测方法，它认为数据的重要程度按时间上的近远呈非线性递减。即近期数据影响价值大，权数亦大；远期数据影响价值小，权数亦小。其公式如下：

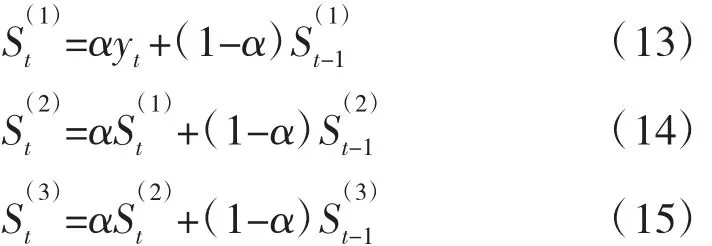
式中：Yi为原始值，这里是指货运量的原始数据；α为平滑系数；t为平滑时间的序别为t时间的一次、二次、三次指数平滑值。三次指数平滑法预测模型公式如下：

式中：t为目前的时间序号；T为预测的超前年份数；为第 t+T 年的预测值；at、bt、ct为常数。其计算公式为：

初始估计值的确定：指数平滑法的计算方法是进行迭代计算，因此在采用指数平滑法预测中

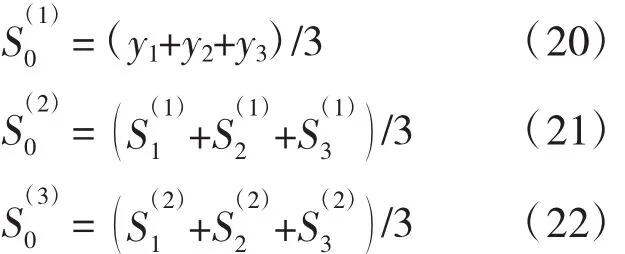
平滑系数的选取：平滑系数α是直接影响预测效果的重要参数，一般根据实际数据序列的特点和经验来考虑。

如果时间序列的长期趋势比较稳定，应取较小值（如 0.1～0.3），如果时间序列具有迅速明显的变动倾向时则应取较大值（如 0.7～0.9），以便使时间序列中最近数据的作用能更多地反映在预测值中。

2 实例分析

某物流公司占地约69 000 m2，物流运输企业规模较小，运输的货物相对单一。主要集中在煤炭、葡萄、葡萄酒和建筑材料等传统行业。其中，2005-2014年公路货运量情况与交通运输业增长率和综合货运量年增长率分别见表1和表2。

表1 公路货运量情况

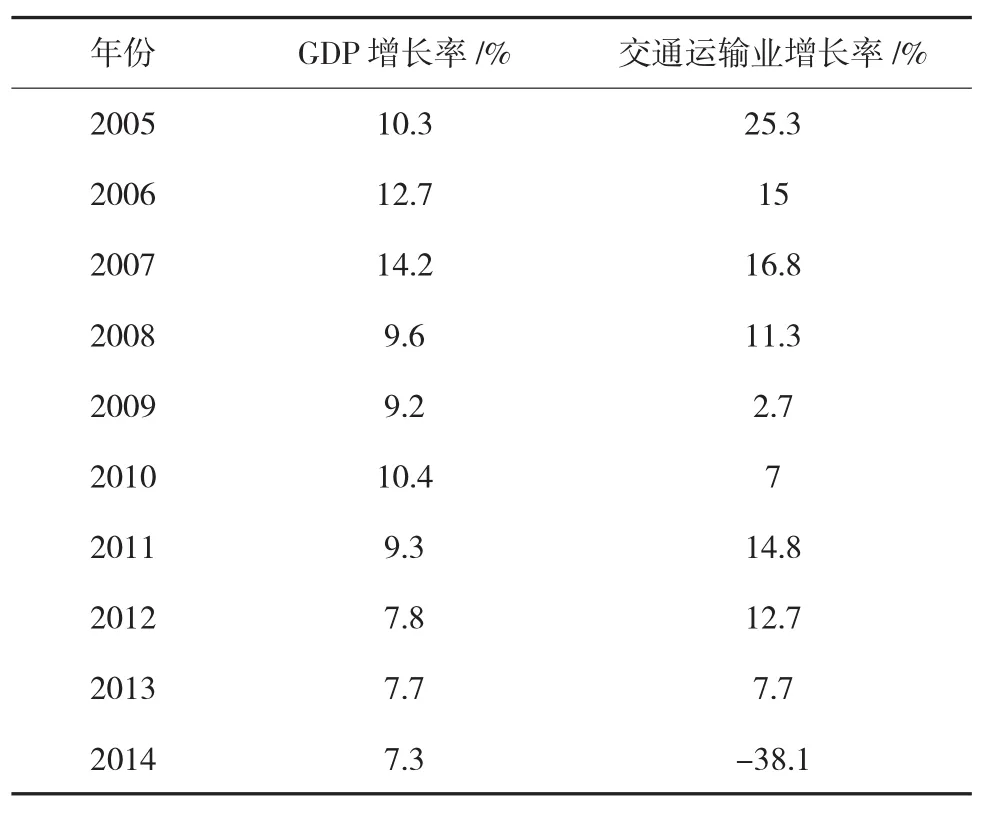
表2 交通运输业增长率和综合货运量年增长率

由表1和表2可确定2015年货运量为492×[1+（7.5%/9.85%）×8.5%]=516（万 t）。

根据式（1）和式（2）可得弹性系数法预测未来特征年公路货运量的预测值，见表3。

根据表1可得原始数列X0（5）=（515，513，494，485，492）。

进行一次累加后得X1（5）=（515，1 028，1 522，2 007，2 499）。

表3 弹性系数法预测值

最后计算得a=-0.124，b=33.14，预测值见表4。

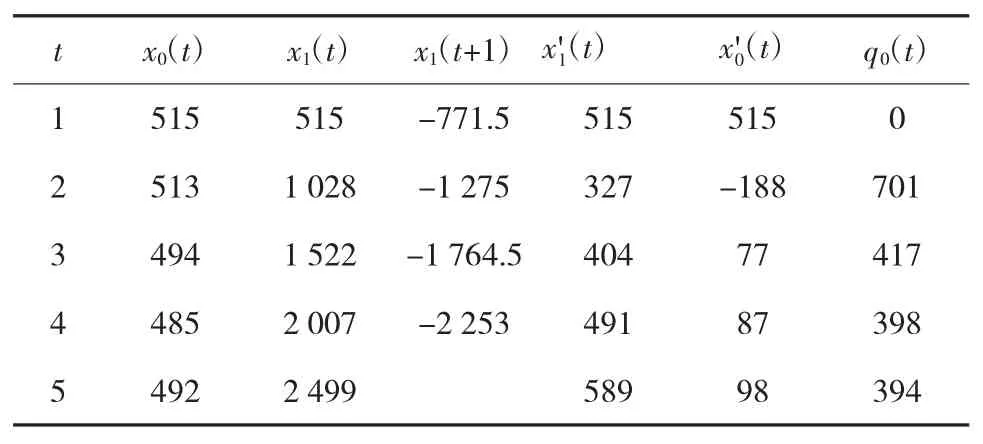
表4 灰色模型预测数据

x0（t）为原始数据，x1（t）为一次灰色序列化得到的生成数系列，为生成数系列的估计值，为总货运量的估计值。该灰色模型是否适用于该货运基地总货运量的预测还需要通过模型精度的检验，预测用残差检验进行说明。残差值为q0（t）。由此可先求得2015年货运量为601万t。

根据灰色理论模型对该货运基地今后特征年的公路货运量进行预测的结果见表5。

表5 灰色模型预测值

当 α=0.1 时 ，=490，=0.1×494+0.9×490=491，=0.1×485+0.9×491=492=0.1×492+0.9×492=492=492，=0.1×491+0.9×492=493，=0.1×492+0.9×493=494，=0.1×492+0.9×494=495，S（03）=494，S（13）=0.1×493+0.9×494=495。

故=491=492，=495，则 a1=492，b1=0.341，c1=0.122，得预测模型为

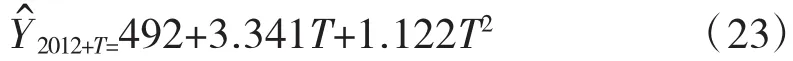
由此预测2013年、2014年货运量分别为496万 t和 503 万 t。同理，当 α=0.3、0.5、0.7、0.9 时对于2013年、2014年预测的货运量见表6。

表6 2013年、2014年预测值 万t

经过预测值与时间年的对比，得知当α=0.1时比较符合实际。故最终指数平滑法的预测模型为当 α=0.1时的模型，即为式（23）。

对特征年2020年、2025年、2030年进行预测结果见表7。

表7 指数平滑法预测值

进行组合预测，它是将几种预测方法的预测结果选取适当的权重进行加权平均的一种预测方法。该方法是建立在最大信息利用的基础上，它集结多种单一模型所包含的信息进行最佳组合，尽可能地提高预测精度，增加预测结果的可靠性。本文拟将多元线性回归分析法的预测结果与灰色预测法的预测结果根据其误差标准差大小进行加权平均，从而得到最终的预测结果。则相关计算公式如下：

首先需要进行标准差的计算，即Sit。其中为t时刻第i种预测方法的预测误差。通过2015年的预测数据和实际数据的对比，可得预测误差见表8。

表8 各方法误差值

故W弹性系数=（1/25）/[（1/25）+（1/10）+（1/5）]=0.117；W灰色模型=（1/10）/[（1/25）+（1/10）+（1/5）]=0.294；W指数平滑=（1/5）/[（1/25）+（1/10）+（1/5）]=0.589。

最终预测值为各方法权重乘以各方法的预测值，见表9。

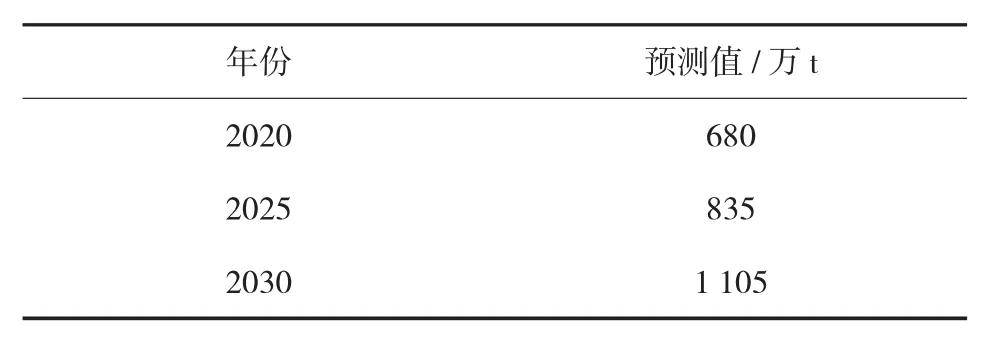
表9 最终预测值

3 结语

弹性系数法、灰色模型法、三次指数平滑法都是常用的物流量预测方法，各自具有独特的优势，预测效果相对较好。本文以这三种方法为基础所构建的组合预测模型，可以更好地预测物流量的变化趋势，起到进一步减小误差、提高预测精度的效果，对物流量预测的相关研究具有一定的应用价值。

[1]Pina A C D,Monteiro B D F,Albrecht C H,et al.ANN and wavelet network meta-models for the coupled analysis of floating production systems[J].Applied Ocean Research,2014,48（13）:21-32.

[2]Kuremoto T,Kimura S,Kobayashi K,et al.Time series forecasting using a deep belief network with restricted Boltzmann machines[J].Neurocomputing,2014,137（15）:47-56.

[3]纪克祥.弹性系数法在交通量预测中的适用性分析[J].交通世界（运输·车辆），2013（Z1）:185-186.

[4]王琰.福州市物流需求预测方法及应用研究[J].物流科技,2016，39（4）:106-110.

[5]张澎,于霞,蒋镇英.基于弹性系数法预测某县货运周转量[J].科技风,2013（22）:73.

[6]宋良,胡正华.基于灰色系统预测方法的供应链联盟伙伴选择研究[J].物流科技,2009,32（3）:130-132.