一种分布式CPS异常检测的无监督图模型

张 锦，程良伦

广东工业大学 自动化学院，广州 510006

1 引言

得益于泛在感知、先进计算以及超强连接，现代分布式信息物理融合系统（CPS）如交通网络[1]、电厂、电网[2]均表现有强大的高效率、鲁棒性以及灵活性的潜力。这一事实在世界各地以及一般工业[3]的研究当中都有提及。然而要实现这样的潜力，针对CPS的有效建模及分析方法必须具备这样的性质：可扩展、鲁棒性、灵活性以及适应性。目前大多数分析方法是在很大程度上依赖于领域知识的需要细致校准和验证的基于规则的模型[4]。

从性能监控和分布式CPS诊断的角度来看，技术上的挑战来自于分布式CPS有着巨大数量的强偶合子系统[5]，同时这些子系统存在不同的操作模式。要对各个子系统分别建模来捕获其复杂的交互作用非常的棘手，但是基于数据驱动的建模方式可以有效地缓解这样的问题[6]。然而，大多数基于数据驱动的建模方式需要大量的正样本（无故障）及所有可能的负样本（如，物理故障或网络异常），负样本在现实系统的生命周期中是很难获取到的。因此，异常检测方法应该有具备如下性质：（1）在没有真正出现故障时识别大多数操作模式的潜力；（2）具备无监督学习能力从标称模式中识别异常模式。此外，物理空间产生的主要是从传感器和执行器而来的连续时间信息，而网络空间主要是处理物理信息而产生离散事件驱动的数据。这种基本属性的差别和信息本质性质的差别，使得目前大多数的方法在处理网络空间和物理空间时，分别进行建模及分析（具体细节可以参考文献[7]）。

在这种背景下，本文提出一种用于分布式CPS在整个系统上异常检测的框架，该框架采用表征CPS各个子系统间相互作用的基于符号动力学的时空特征提取方案。符号动态过滤（SDF）是一种复杂系统的数据驱动建模方式，其采用一种称为数据抽象的统一表示描述不同类型的数据，在描述不同类型的数据方面具有优势。数据抽象预处理及对相关变量（如，传感器的时间序列）进行数据空间划分有助于对网络和物理子系统进行统一建模。由SDF捕获的特征用于构造时空模式网络（STPN）[8]——最近提出的一种因果关系图模型概念。通过训练这样的模型，本文为检测低概率事件或异常模式提出了一个推理方案。

2 背景及基本理论

2.1 时空模式网络

符号动态过滤（SDF）已被证明从异常检测和模式分类的时间序列数据中提取关键词是非常有效的[9]。其核心思想是，从一个过程发出的符号序列（如，离散时间序列）可近似为D阶马尔可夫模型（D-Markov model），用于捕获过程当中潜在的关键行为。离散化或符号化的过程成为分区[9]。基于不同的目标函数，一些研究当中提出了不同的分区方法：如均匀分区（UP）、最大熵分区（MEP）、最大目标离散化（MBD）等[10]。本文采用的是均匀分区方式。D阶马尔可夫模型本质上是一个概率有限状态自动机（PFSA），可以由状态（表示数据空间的各个部分）以及状态之间的转换概率（可从数据中学习得到）描述。

时空模式网络（STPN）可定义如下：

一个STPN可以由一个四元组表示WD=(Qa,Σb,Πab,Λab)，a,b表示STPN的节点。

（1）Qa={q1,q2,…,是与符号序列Sa相对应的状态集。

（2）是符号序列Sa的集合。

（3）Πab是一个| Qa|×| Σb|的符号生成矩阵，第ij个元素表示在符号序列中从状态qi转变时在符号序列中找到符号σi的概率。自身符号生成矩阵称为原子模式（APs），当a=b时；交叉符号生成矩阵称为交互模式（RPs），当a!=b时。

（4）Λab表示一个交互模式重要性指标（或因果关系的程度），可以采用基于信息论的指标，如传递熵或互信息来定义。

一个STPN可以用图1描述。

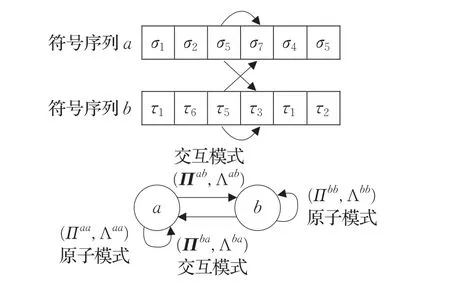
图1 子系统自身行为及子系统间交互行为的原子模式（APs）和交互模式（RPs）提取

2.2 受限玻尔兹曼机

受限玻尔兹曼机（RBM）近期在深度学习领域的无监督特征提取中受到了很大的关注[11-12]。受限玻尔兹曼机的基本结构如图2的无监督学习层（左上角）。作为基于能量的模型，通过学习权重和偏执，使得系统在正常执行期间观察到的特征属性获得低能量（或高概率）。考虑由一组可见变量v=(v1,v2,…,vD)和一组隐藏变量h=(h1,h2,…,hF)描述的系统状态。变量的值根据实际需求可以是二值变量或实数变量。这些变量确定了系统的一个特定状态和与其相关的能量值E(v,h)。能量值是变量之间连接权重的函数（对于RBM内部连续仅考虑可见变量，不考虑隐藏变量），偏执则是变量的函数。

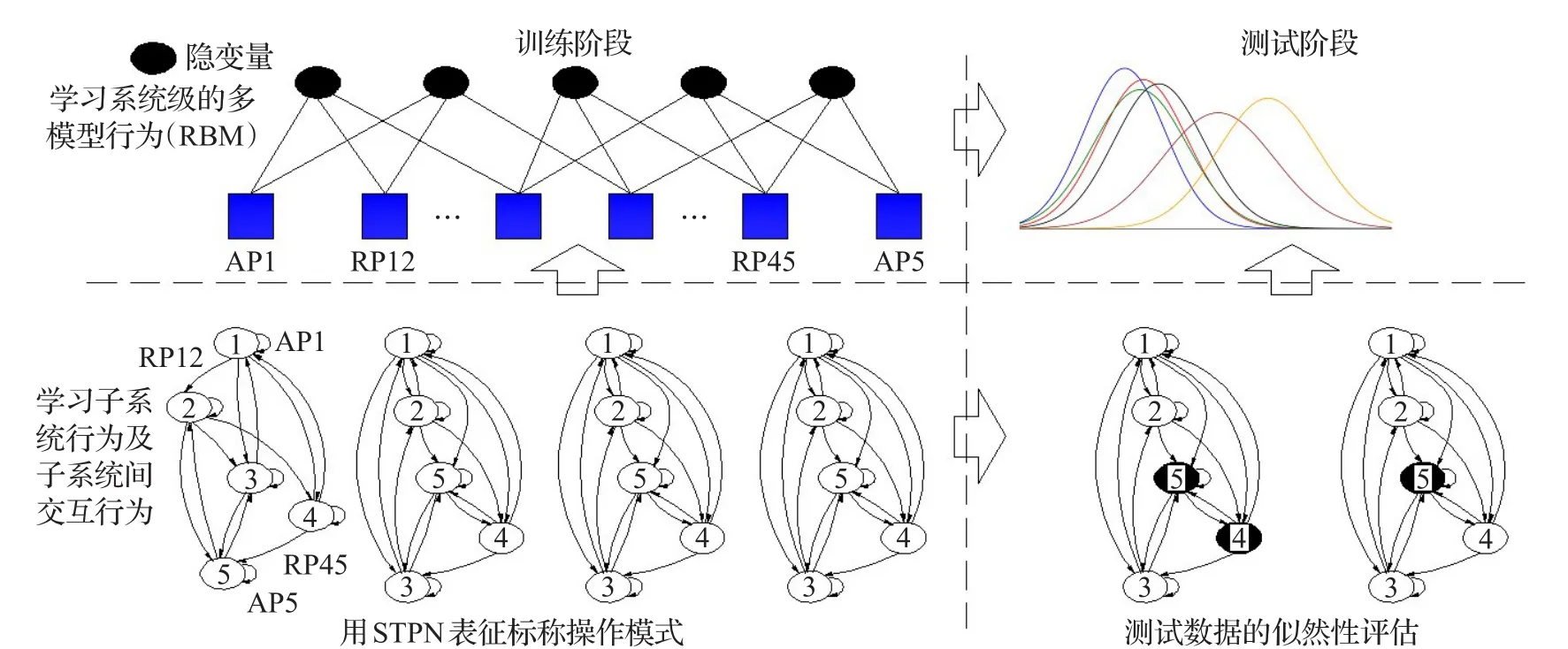
图2 一个基于数据驱动的分布式CPS系统异常检测框架

通过以上描述可得到，状态 p(v,h)的概率仅依赖于连接(v,h)的能量，同时满足玻尔兹曼分布：

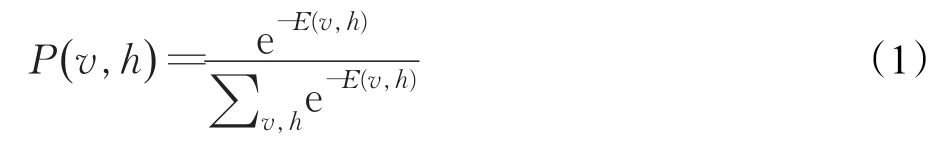
在训练过程当中，通常最大化训练数据的似然函数来得到权重和偏置。

3 提出模型

图2描述了以上提出的基于数据驱动的系统异常检测框架。在训练阶段，学习STPN+RBM模型的步骤如下：

（1）从多元训练符号序列中学习APs和RPs（单节点行为和节点对的交互行为）。

（2）考虑来自训练样本的短符号子序列，同时对其进行评估求得Λij，i和 j对应每一个子序列。

（3）对于每个子序列，基于在Λij中用户设定的阈值，为每个AP和RP分配状态0或1；从而每个子序列转换成一个长为L的二值向量，L=#AP+#RP。

（4）然后使用RBM对APs和RPs对应的可见层的节点进行系统行为建模。

（5）将从子序列生成的二值向量作为特征进行训练RBM模型。

3.1 训练STPN+RBM模型

考虑训练一个多元时间序列（上文提到的标称操作数据），X={XA(t)},t∈N,A=1,2,…,f,f是时间序列变量的个数或维数。首先，执行符号化及学习PFSA来抽取原子模式及交互模式，将其用于对应的 f个顶点和 f2条边的时空模式网络（STPN）。在这种情形下，定义符号序列集为S={SA}。然后，定义一个短序列X={XA(t)},t∈N*,A=1,2,…,f，其中 N*是 N 的子集。本质上讲，从整体训练数据中按不同的时窗（由N*表示）抽出的序列均可视为短序列。类似之前的定义，通过不同时间窗抽取的一组符号子序列可以定义为S={SA}。

下一步是为从整个时间序列提取的每个短子序列计算Λij。虽然基于信息论的度量是一个非常好的选择，但这种度量方式需要大量的样本点，因此在异常检测这种缺乏负样本的场景当中不太适用。本文中采用文献[13-14]中提到的统计推理策略度量方式，该度量的计算步骤分两个阶段：建模过程、预测过程。

建模过程：对整个训练数据的一个STPN可以描述为WD=(Qa,Σb,Πab,Λab)。整个符号序列集合定义为S；整个序列的状态表示产为Q={Qa,a=1,2,…,f}；一个模式的状态Πab取决于符号序列Qa及序列的状态Sb。在该步骤，Πab的每一行都初始化为一个随机向量。对于第m行，随机向量的先验概率密度函数| {Qa,Sb}由联合状态符号序列{Qa,Sb}决定，并且服从狄利克雷分布。概率密度函数如下：

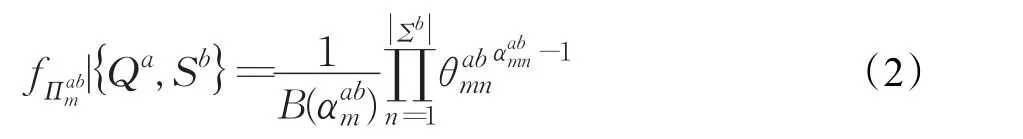
其中是随机向量的一个实现：

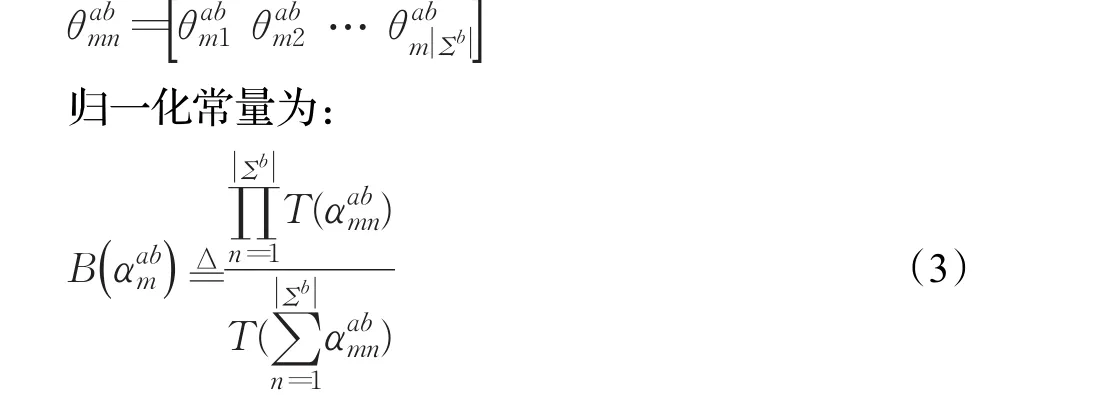
其中

符号序列的时间长度；是在状态之后估计的。

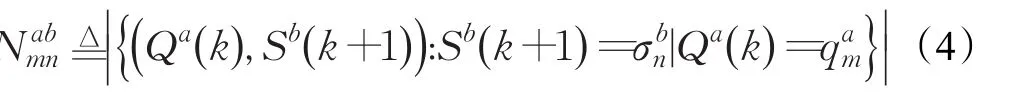
Qa(k)是状态序列Qa的第k个状态；Sb(k +1)是符号序列Sb的第k+1个符号。

从而公式（3）可以改写为：

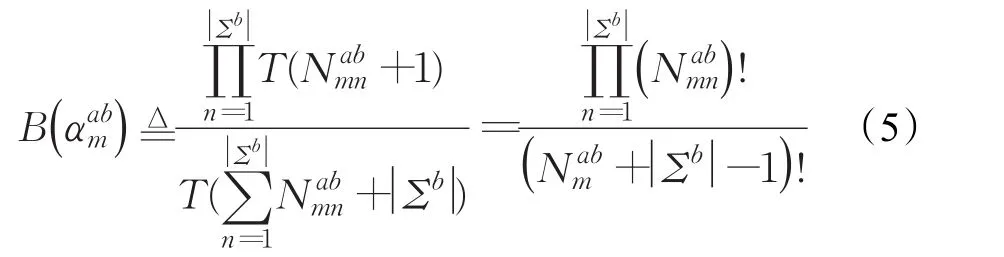
其中T(n)=(n-1)!。

根据马尔可夫的属性可知的行向量之间统计意义上相互独立。通过公式（2）、（5）可以求得概率转换矩阵关于状态符号序列{Qa,Sb}的条件联合概率密函数：

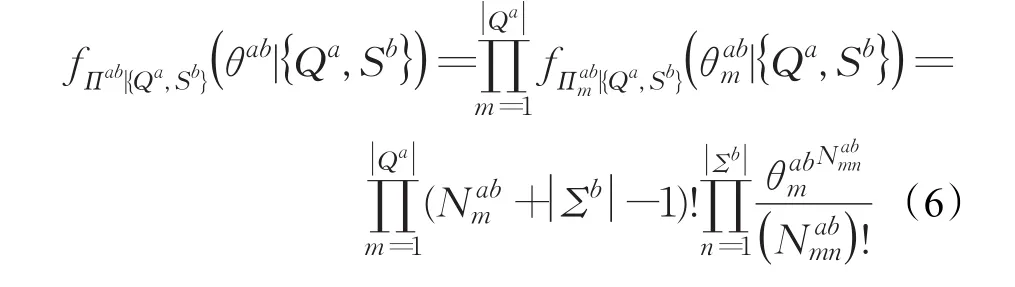
其中

预测过程：在对整个训练序列集建完模之后，预测的主要目的是计算给定的子序列（由Q和S描述）的度量Λab(Q)。度量的值大小表示模式Πab的重要度或短子序列a→b的因果关系。根据这一观点，可以用公式表示如下：

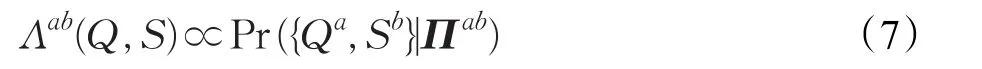
当转换矩阵是已知的情况下，联合状态符号子序列的概率是独立多项式分布的乘积：

的定义与上文对子序列的定义一致。

做与文献[13]中类似的推导，可以得到度量矩阵：

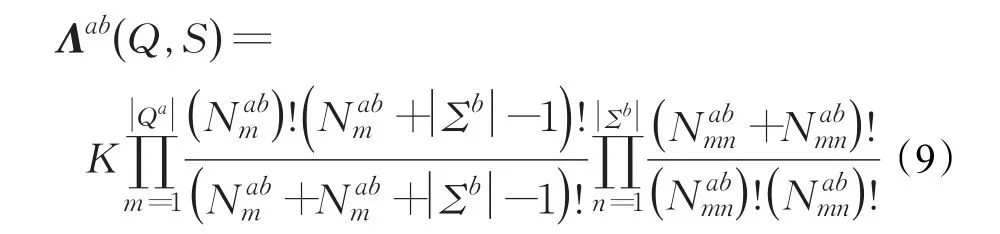
其中K是一个常量系数。

根据公式（9）可以对相应短子序列获得 APs和RPs重要性指标。为了训练整个系统的RBM模型，可进一步将APs和RPs的度量指标标准化为二值状态（低值置0，高值置1）。注意到，每个子序列所有的APs和RPs一起形成长度为L=f2的二值向量(L=#AP+#RP，其中：#AP=f,#RP=f*(f-1))。一个这样的二值向量就是一条用于训练系统级RBM的样本（有f2个可见单元），从不同子序列抽取的许多这样的样本则构成了整个训练样本集。然后如图2所示，使用最大似然估计来训练RBM。本文采用的方式是将度量矩阵强制转换成二值向量来简化RBM的训练，对于训练来说，这一过程是非必须的。

说明：在STPN学习过程中，加入一个滞后时间，STPN+RBM可以处理可变时滞系统，同时会大降低整个学习过程的复杂性。这与递归神经网络（RNNs）类似。

3.2 异常检测过程

异常检测过程采用RBM——一个基于能量的概率图模型的自由能概念。RBM的能量函数可以定义如下：

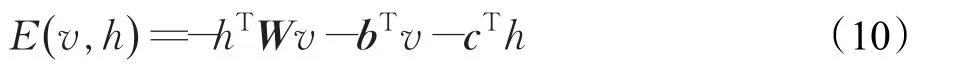
W是隐藏单元的权重，b和c分别是可见单元和隐藏单元的偏置。

利用RBM的权重和偏置，可以获得自由能的表示：

自由能的另一种表达可以是[8]：

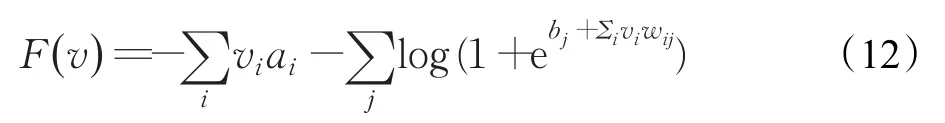
在训练阶段，最小化能量函数则可以得到模型的权重和偏置。通常异常模式应该表现为低概率（高能量）的状态。因此，在测试阶段，可以根据模型对样本的概率估计来检测异常模式。在做异常检测的过程中，测试子序列按照训练数据的转换方式，将其转换为 f2维二值向量。对多个测试子序列进行估计，则可以得到自收能的分布情况。对于标称模式，自由能的分布应该与训练数据的分布比较接近，对于异常模式，自由能的分布将不同于训练数据的分布。

对比训练数据和测试数据的分布，可以采用KL散度这一指标[15]。因为KL散度是一个非对称的描述两个分布P和Q的指标，是一种非对称的信息度量。因此这里可以采用一种对称KL距离的度量，即：

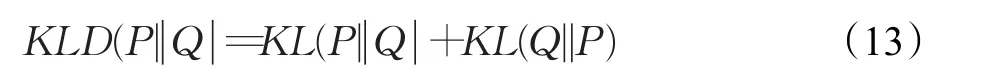
4 实验与讨论

4.1 数据生成

向量自回归（VAR）是处理多个相关指标分析与预测最易操作的模型之一，在多元时间序列数据中非常的灵活与简单，在经济学等学科中得到了广泛的应用[16]。向量自回归的基本模型(Y(t)=yi,j,i=(1,2,…,f),t∈N)可以用如下公式表示：其中 p是时间滞后阶数，Ai,j是第 j个时间序列对第i个时间序列的影响系数，μt是均值E()μt=0；协方差矩阵E( )

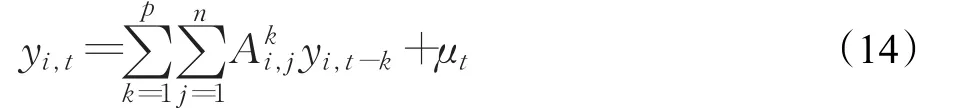
μtμt=Σμ的噪声。在本文中，将使用VAR模型生成多变量数据用于异常检测模型的仿真。5个顶点的层次结构表示各个顶点之间不同的相互作用。各种相互作用表示分布式CPS中的标称条件和异常条件。生成两组数据用于两种情况的分析工作：（1）定义6种模式，第1种属于标称模式，其余5种为异常模式；（2）定义8种模式，前3种属于标称模式，其余5种为异常模式。第2种情况用于模拟CPS中多个标称操作模式的情形。

然后从VAR生成的代表不同交互模式的原始数据中训练得到模型STPN。对于无监督RBM的训练过程，仅仅从标称模式中学习权重和偏置。训练好的RBM模型将用来对所有操作模式的数据计算关于不同模式输入的自由能。最终对多个服从高斯分布的测试数据进行自由能的评估，对比评估结果。

4.2 实验一分析：单标称模式

图3中表示了预定义的图模型，异常发生的情况是一个顶点出错并且与其连接的边丢失。在实验中，采用标称条件的原子模式和交互模式数据训练RBM模型。然后将训练好的RBM模型用于6个模式的所有测试数据，产生各个自由能的概率分布，如图4。从图中可以看出，标称模式的自由能分布与训练数据自由能分布非常接近，其他模式的自由能分布则非常的不同。这表明异常模式具有高自由能，同时发生的概率低。计算分布之间的相关性得到，训练/标称模式的自由能分布与所有其他测试模式的自由能分布之间的KLD指标分别为：

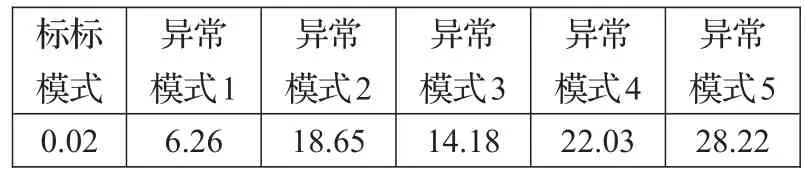
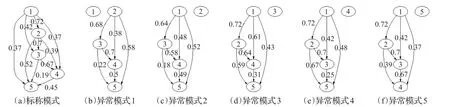
图3 合成数据的图模型

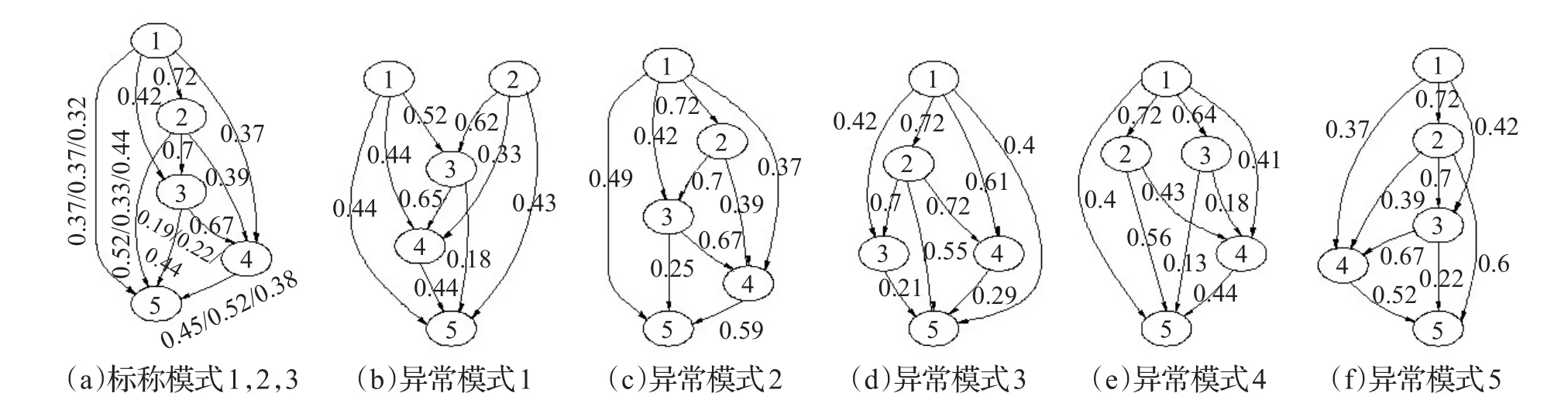
图4 合成数据的图模型

4.3 实验二分析：多标称模式

与先前的情况类似，预定义的图模型如图5，自由能的分布如图6。与预期的一致前三种模式的自由能分布类似于训练数据的自由能分布。KLD分别为0.052、0.263、0.639。该图还显示，对于4至8，KLD值分别为5.06、5.46、6.24、4.91、9.97可以清楚地鉴定异常模式。总体上，结果清晰地表明，所提出的框架可以捕获在一个模型内的多个标称模式，同时还可以有效地检测因果关系模式的轻微变化。

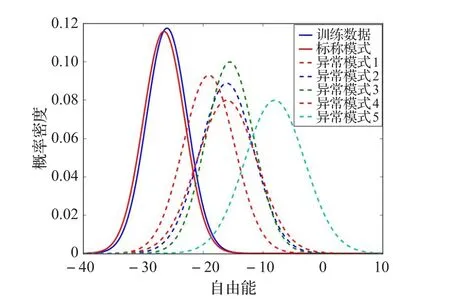
图5 RBM模型对各种模式（单标称模式）的自由能分布

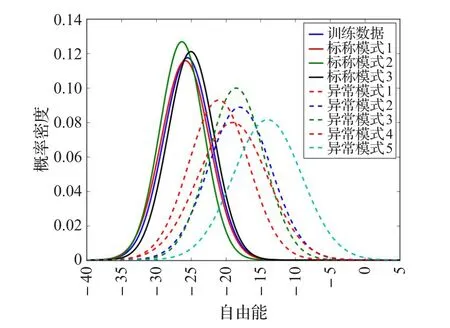
图6 RBM模型对各种模式（多标称模式）的自由能分布

4.4 讨论

在分布式CPS当中，其异常机制、特点和持续时间各不相同，这使得异常检测非常困难，特别是对所有可能的异常标记数据的收集。本文提出的框架中只需要正例样本，异常检测则看作是以标称数据为条件的低概率事件。从实验的结果可以看出，异常条件下的自由能分布不同于标称条件下自由能的分布，可以使用诸如KLD的变化来度量。此外，它有潜力监控从小的物理退化到严重故障或网络攻击，其中小KLD表示因果模式的轻微变化，可预示早期退化或故障前兆。

5 结束语

本文提出了一个系统级的CPS异常检测框架，该框架是一种基于数据驱动的方法，但不同于监督学习方法，不需要标记好的正负样本。该框架包括了一个时空特征提取方法用于发现和表征CPS各子系统之间相互作用的因果关系，以及使用RBM的全系统模式的自由能估计。以上实验表明，本文所提出的方法可以在单个概率图模型中捕获多个不同的标称模式，并通过识别低概率事件来检测异常模式。同时准确性和鲁棒性方面也表现良好。

目前的工作重点主要集中在检测异常情况以及量化假警报，进一步的工作将扩展到：（1）将图模型应用到各种异常情况的根本原因分析上；（2）采用叠加RBM的方法捕获更复杂的标称模式；（3）检测分布式CPS中同时出现的多个故障。

[1]Work D，Bayen A.Impacts of the mobile internet on transportation cyber-physical systems：Traffic monitoring using smartphones[C]//National Workshop for Research on High-Confidence Transportation Cyber-Physical Systems：Automotive，Aviation，and Rail，2008：18-29.

[2]赵庆周，李勇，田世明，等.基于智能配电网大数据分析的状态监测与故障处理方法[J].电网技术，2016，40（3）：774-780.

[3]Bradley J，Barbier J，Handler D.Embracing the Internet of everything to capture your share of$14.4 trillion[D].CISCO White Paper，2013.

[4]文成林，吕菲亚，包哲静，等.基于数据驱动的微小故障诊断方法综述[J].自动化学报，2016，42（9）：1285-1299.

[5]Sanislav T，Miclea L.Cyber-physical systems concept，challenges and research areas[J].Control Engineering&Applied Informatics，2012，14（2）：28-33.

[6]Choi A，Zheng L，Darwiche A，et al.A tutorial on Bayesian networks for system health management[J].Machine Learning and Knowledge Discovery for Engineering Systems Health Management，2011，10（1）：1-29.

[7]Krishnamurthy S，Sarkar S.Scalable anomaly detection and isolation in Cyber-physical systems using Bayesian networks[C]//Proceedings of ASME Dynamical Systems and Control Conference，2014.

[8]Jiang Z，Sarkar S.Understanding wind turbine interactions using spatiotemporal pattern network[C]//Proceedings of ASME Dynamical Systems and Control Conference，2015.

[9]Rao C，Sarkar S，Ray A，et al.Comparative evaluation of symbolic dynamic filtering for detection of anomaly patterns[J].Signal，Image and Video Processing，2009，3（2）：101-114.

[10]Sarkar S，Srivastav A，Shashanka M.Maximally bijective discretization for data-driven modeling of complex systems[C]//American Control Conference，2013：2674-2679.

[11]Hinton G，Salakhutdinov R.Supporting online material for reducing the dimensionality of data with neural networks[J].Science，2006，313：504-507.

[12]Roux N，Bengio Y.Representational power of restricted boltzmann machines and deep belief networks[J].Neural Computation，2008，20（6）：1631-1649.

[13]Akintayo A，Sarkar S.A symbolic dynamic filtering approach to unsupervised hierarchical feature extraction from time Series data[C]//American Control Conference，2015：5824-5829.

[14]Sarkar S，Mukherjee K，Sarkar S，et al.Symbolic dynamic analysis of transient time series for fault detection in gas turbine engines[J].Journal of Dynamic Systems Measurement&Control，2012，135（1）.

[15]Kullback S，Leibler R A.On information and sufficiency[J].The Annals of Mathematical Statistics，1951，22（22）：79-86.

[16]Goebel R，Roebroeck A，Kim D，et al.Investigating directed cortical interactions in time-resolved FMRI data using vector autoregressive modeling and Granger causality mapping[J].Magnetic Resonance Imaging，2003，21（10）：1251-1261.