原位自生(TiB+TiC)/Ti-1100复合材料的高温力学性能及强化机制

，， ， ，新宽，， (. ， 00093； .交通大学 ， 00040)

1 前 言

钛合金具有密度小，比强度高，耐蚀性、热强性和持久性优异等特点，是理想的飞机发动机用材。提高航空发动机的压缩比可有效提高飞机的飞行速度和灵活性，提高发动机的推力和压缩，从而减轻发动机结构重量，提高发动机的结构效率和燃气温度的设计要求，促使材料向轻质、耐高温方向发展。随着高性能发动机的发展，高温钛合金的使用温度也逐渐提高，目前先进的高温钛合金的使用温度可以达到600℃[1]。然而，当使用温度超过600℃时，钛合金的强度以及蠕变抗力急剧下降，极大地限制了钛合金向更高的使用温度发展。

由于在现有的基础上提高高温钛合金的使用温度存在着较大的困难，因此，钛基复合材料(TMCs)脱颖而出。钛基复合材料是指在钛或钛合金基体中引入增强体所形成的一种复合材料。美国80年代研制成功的用于航空发动机的Ti-1100高温钛合金(Ti-6Al-2.75Sn-4.0Zr-0.4Mo-0.45Si)以其在600℃仍具有良好的蠕变性能和断裂韧性而受到人们的瞩目[2-4]，本实验采用Ti-1100合金作为复合材料的基体。在增强体的选择中，TiC 和 TiB 具有熔点高、与钛相容性好、密度低、弹性模量高等特点，是钛基复合材料较为理想的增强体[5-7]。本实验原位合成了以Ti-1100合金为基体的(TiC+TiB)钛基复合材料[8-9]，目的在于研究钛基复合材料微观结构及其高温力学性能的改变，并通过对复合材料中各种强化因素的测试与计算来研究其强化机制[10]。

2 实验方法

实验所用原材料主要有：一级海绵钛(>99.5%)，B4C粉末(>99.95%)，碳粉(>99%)，海绵锆(>99.5%)，结晶硅(>99.95%)，铝丝，以及其它元素的中间合金，如Ti-Sn，Al-Mo等。首先按比例称取一级海绵钛、B4C粉末、合金元素以及各中间合金，将其混合均匀，接着利用压机将混合均匀的原料压制成电极棒。然后将电极棒放入真空自耗电弧炉中进行熔炼，为了保证其化学成分的均匀性，在制备过程中至少进行三次熔炼。在熔炼过程中，发生如下化学反应：Ti+B4C→4TiB+TiC。本文分别设计了Ti-1100合金、固溶0.28% C的Ti-1100合金和(TiB+TiC)/Ti-1100三种不同的样品，具体名义成分见表1。

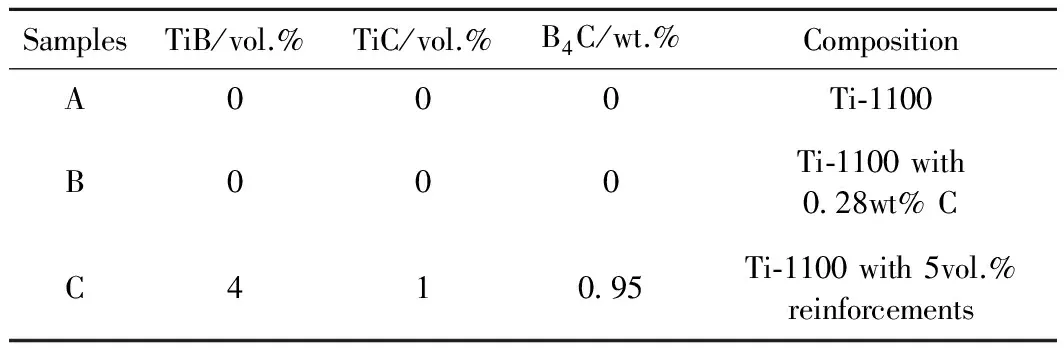
表1 三种样品的名义成分Table 1 Composition of the samples

计算复合材料中B4C粉末添加量(见式(1))。

(1)

在上式中，iv，iM，ρR和ρM分别代表增强体的体积分数，增强体的质量分数，增强体的密度和基体合金的密度。

材料的光学金相试样采用传统方法制备，在莱卡金相显微镜上进行观察。物相分析在D-max IVA 全自动X射线衍射仪上进行。高温拉伸试验在Zwick-100KN高温材料试验机上进行，拉伸试样是从铸锭中机加工出厚2.0mm，长50.0mm的薄板，试验温度分别为550、600、650℃，应变速率为5.0×10-3s-1。透射电镜(TEM)样品用线切割从试样上切取0.3mm厚的薄片，手工磨至0.03mm后，采用高氯酸∶醋酸=1∶9的电解抛光液在293～303K温度下进行双喷电解抛光，样品观察在JEM-2010透射电镜上进行，加速电压为200kV。

3 结果与讨论

3.1 材料的显微组织和相分析

图1为5%(TiB+TiC)/Ti-1100复合材料的X射线衍射图谱。图中显示的结果表明B4C与基体反应生成了TiB和TiC。图2为5%(TiB+TiC)/Ti-1100复合材料的显微组织，图中显示增强体均匀地分散在Ti-1100基体中，且纤维增强体取向各异。图3所示为TiC和TiB的TEM像以及对应的选区衍射图，从图中可以看出TiC、TiB和基体之间结合良好，没有明显的反应层，且TiC和TiB的形貌有明显的不同。其中TiC颗粒的直径约为400nm；TiB纤维的直径约为200nm，平均长径比约为11.4。

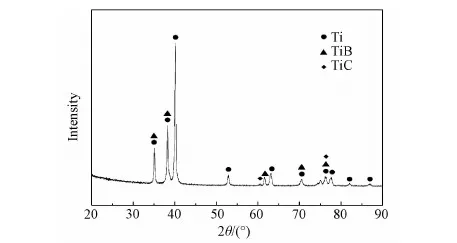
图1 5% (TiB+TiC)/Ti-1100复合材料X射线衍射图谱Fig.1 XRD pattern of 5% (TiB+TiC)/Ti-1100 composite

图2 5%(TiB+TiC)/Ti-1100复合材料的光学显微图像(未腐蚀)Fig.2 Optical micrograph of 5%(TiB+TiC)/Ti-1100 composite(unetched)

3.2 高温拉伸性能

表2给出了基体合金和复合材料在不同温度下的抗拉强度、屈服强度和断裂延伸率。分析表中数据可得，复合材料的高温强度较基体合金有显著提高。这在一定程度上归因于碳的固溶强化，还包括增强体的形态和体积分数、纤维增强体的取向和增强体的界面等因素。

图3 5%(TiB+TiC)/Ti-1100复合材料中增强体TEM图像 (a) TiC； (b) TiBFig.3 TEM micrographs of the reinforcements (a) TiC; (b) TiB

表2 基体合金和复合材料的高温拉伸性能Table 2 Tensile properties of matrix and composites at different testing temperatures

3.3 强化机制

3.3.1TiB纤维增强体的强化机制 由Cox[11]提出，经Nardone和Prewo[12-13]改进的剪滞模型，可用来计算短纤维增强体取向与拉伸方向一致时复合材料的屈服强度。其屈服应力的增加可表述为：

Δσ=σym0.5V·l/d

(2)

式中，σym代表基体合金的屈服强度，V是纤维增强体的体积分数，l/d是纤维增强体的长径比。

式(2)描述的是纤维增强体取向完全统一，且都与拉伸方向一致的情况。但是，在我们实验用复合材料中TiB纤维增强体并不符合这种情况，因此需要考虑TiB纤维增强体的取向分布。Fukuda和Chou[14]提出一种概率论，可用于检测纤维长度及取向分布对纤维增强复合材料强度的影响。因此，考虑到TiB纤维增强体取向杂乱无章时，ΔσTiB可修改为：

ΔσTiB=σym0.5V·l/d·C0

(3)

式中，C0为纤维增强体取向因子，取值范围0～1。C0的表达式[12]：

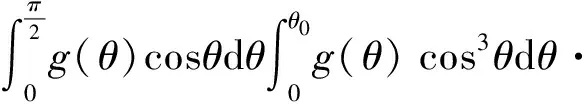
(4)

式中，θ是纤维增强体轴线与拉伸方向的角度，g(θ)是基于纤维增强体位向分布的概率密度分布函数，h(l)是纤维增强体长度分布概率密度分布函数，β是小于1的常数(确定纤维是否为桥接纤维)[15]，l和lc分别代表纤维增强体的平均长度和临界长度。

其中纤维增强体长度对复合材料的力学性能有显著影响。有关应力随纤维长度的变化规律最早由Rosen[16]用剪切滞后法来研究，该方法假定基体只传递剪应力，不传递正应力，假设认为纤维周围的基体为理想的塑性材料，则界面剪应力沿纤维长度是常数，其值等于基体的剪切屈服应力τs，得到：

(5)

然而纤维应力不能超过一极限值，能够达到最大纤维应力的最小纤维长度定义为载荷传递长度lc，即纤维临界长度。

(6)

式中，d为纤维直径，τi为界面剪切强度，σf为纤维拉伸强度。所以当纤维的长径比大于临界长径比时，纤维才能最大程度地传递载荷，达到强化效果。

在本次研究中TiB纤维的平均长径比为11.4，在室温下钛基复合材料的TiB纤维临界长径比为2.07[17]。虽然临界长径比随温度的升高而增大，但TiB纤维绝大多数为细长棒状，即使温度高达650℃，其大部分TiB纤维仍处在高于临界长径比的状态，因此为了简化模型，认为所有TiB纤维都是桥接纤维，那么β值为0，公式(4)可简化为：

(7)

由于在复合材料中TiB纤维是随机生成的，TiB纤维角度取向从0°到90°随机均匀分布，因此概率密度g(θ)是一个常数，其积分值为1。

(8)

(9)

将式(9)代入式(7)中，

(10)

经计算，C0=0.2702。

3.3.2TiC颗粒增强体的强化机制 颗粒增强体对金属基复合材料的强化因素可以归于两点：(1)颗粒承担载荷——颗粒增强体可通过应力传递效应直接从基体分担外加应力[18]；(2)颗粒强化位错——颗粒增强体会引起基体中附加位错的形核[12-13,19]。Ramakrishnan[20]提出一个分析模型，其模型结合了改进后的剪滞模型和位错密度强化模型，可预测屈服强度，其表达式为：

σyc=σym(1+f1)(1+fd)

(11)

式中，f1代表颗粒增强体承担载荷时的改善因子，fd代表颗粒增强体强化位错时的改善因子。根据式(11)，颗粒增强体TiC对复合材料强度增加的贡献可表示为：

ΔσTiC=σym[(1+f1)(1+fd)-1]

(12)

f1的通用表达式为[12,21]：

f1=0.5VTiC

(13)

fd的通用表达式为：

fd=Δσdis/σym

(14)

VTiC表示TiC颗粒的体积分数，Δσdis表示位错强化对屈服强度的提升，其表达式为[22]：

(15)

式中，Δσor代表Orowan应力，Δσthe代表由于基体和增强体的热膨胀系数不一致而造成的应力增量，Δσgeo代表由应变梯度效应(与调节基体和增强体之间塑形变形比例失当所需的几何必需位错分布相联系)引起的应力分布。图4所示为变形后试样中位错分布的TEM形貌。从图中可以看出，在TiC颗粒周围的位错密度要远大于晶粒内部，且大于图3(a)中TiC颗粒周围的位错，说明在拉伸变形过程中试样中形成了几何必需位错[23]。

图4 试样拉伸后位错分布的TEM图像Fig.4 TEM micrograph of the dislocations in the deformed sample

Orowan应力Δσor可以用Orowan-Ashby方程式描述[24]：

(16)

式中，Gm和b分别为金属基体的切变模量和柏氏矢量[25]，r是粒子半径，λ是粒子间距，其表达式为[26]：

(17)

dp表示粒子直径，Δσthe的表达式为[27]：

(18)

其中k是常数，约等于1.25，ρ是增强的位错密度，其表达式为：

(19)

式中，Δα为基体和增强体颗粒的热膨胀系数之差，ΔT为加工温度和试验温度之差。最后，由几何必需位错引起的应力增量Δσgeo表达式为[28]：

(20)

式中，ξ是一个几何因子(～0.4)，ε是金属基体的塑形应变。在屈服强度的计算中，ε取值0.002。

3.3.3碳固溶体的强化机制 C的加入量对基体合金β转变温度的影响可以通过Ti-Al-C三元相图来解释。可以将合金中所含有的α相稳定元素用相应的铝当量表示，根据基体合金的名义成分计算得本实验制备的Ti-1100基体合金的铝当量为7.7。参考Ti-8Al-C三元相图中C在β相中的最大固溶度约为0.28%。如表2所示，当Ti-1100基体合金中固溶0.28% C后，强度有明显的提升。根据试样A和试样B屈服强度之差，可计算出碳固溶体的强化效应(Δσssc)。经计算，Δσssc在550、600、650℃下分别为19.4、19.8及16.3MPa。

3.3.4多种强化因素耦合 对于混合增强复合材料，前人通过大量的实验和计算机模拟来研究不同的增强体叠加起来对复合材料的影响[29-31]。这些研究表明，如果合金基体中存在两种或更多种增强体，那么材料总的临界分切应力τ就是单个类型强化因素的叠加。N种强化因素耦合的近似表达式为[29,31-32]：

(21)

式中，指数q介于1(线性加法准则)和2(Pythagorean加法准则)之间，不同的q值代表不同的增强体叠加强化效应。τi是所有强化因素中的一部分，受增强体数量的影响，其值随增强体体积分数的增加而增加[32]。在目前的研究中，TiB纤维和TiC颗粒的叠加强化效应可近似表达为：

(22)

那么原位自生(TiB+TiC)/Ti-1100复合材料的屈服强度σyc可表示为：

(23)

式中，σym不是指Ti-1100基体合金(试样A)的屈服强度，而是指Ti-1100中固溶0.28% C(试样B)后的屈服强度。

3.3.5数据整合计算 根据表3中的参数，可以计算出ΔσTiB及ΔσTiC的值(表4)。由于ΔσTiB及ΔσTiC在复合材料中的体积分数并不高，在550、600、650℃下Δσssc与ΔσTiB及ΔσTiC的值相差并不大，因此碳固溶体的强化效应不容忽视。

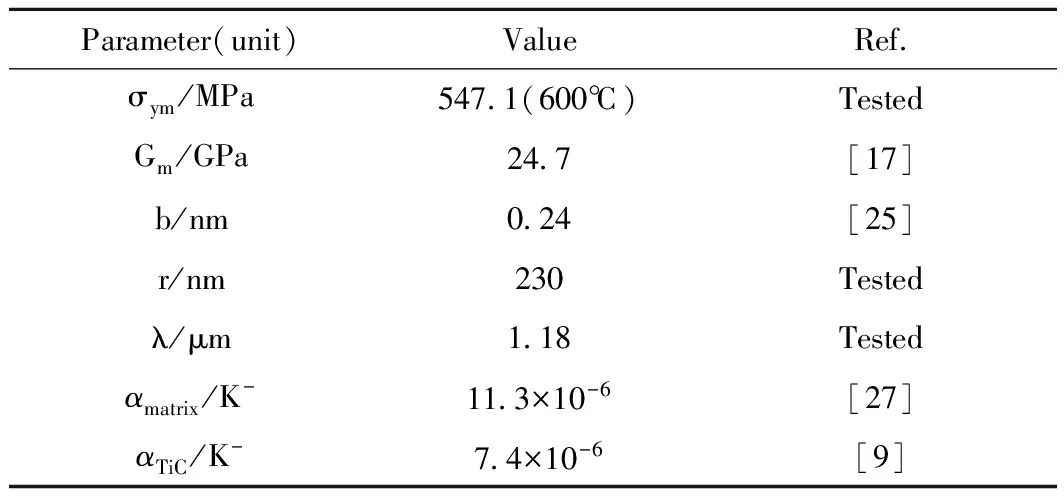
表3 计算用参数Table 3 Parameters used in the calculation

表4 不同温度下的ΔσTiB，ΔσTiC 和Δσssc 的值Table 4 Calculated values of f1, fd, ΔσTiB, ΔσTiC and Δσssc at different testing temperatures

拉伸后的样品在扫描电镜下观察，发现断口附近大部分TiB纤维产生了断裂，说明在拉伸过程中，TiB纤维比较细长而处在临界长径比之上，属于高效承载状态，传递了基体中的应力。而在断口附近并没有观察到破碎的TiC颗粒，却有许多位错缠结在TiC颗粒周围；并且根据表4中的数据(600℃)，fd值大约是f1值的6倍，说明TiC颗粒承担载荷的影响作用十分有限，而其主要通过强化位错效应起作用。

最终TiB，TiC/Ti-1100复合材料屈服强度值要结合式(3)、(12)、(22)、(23)来进行计算。图5中,线A代表实验数据，线B、C、D是利用数学模型计算出的数据，其结合式(22)、(23)分别对应q的值为1、2、1.32。从图中可以看出，当q的值为1时，计算值远远大于实验值，说明TiB,TiC/Ti-1100复合材料的强化机制不是TiB纤维和TiC颗粒强化效应简单的线性叠加。当q的值为2时，计算值又小于实验值。而当q=1.32时，计算值与实验值十分接近，表明建立的研究强化机制的数学模型可以用来预测钛基复合材料的屈服强度。

图5 在不同温度下TMCs屈服强度的实验值和计算值Fig.5 Experimental values and calculated values of yield strengths of the TMCs at different testing temperatures

4 结 论

1.原位自生钛基复合材料中TiB,TiC增强体均匀弥散地分布于基体材料中，其中TiC呈颗粒状，TiB呈纤维状，且TiB纤维轴向角度取向从0°到90°随机均匀分布。

2.原位自生钛基复合材料的高温力学性能相对基体合金有较大提高，其屈服强度的提高主要受益于TiB纤维的传递载荷、TiC颗粒的强化位错和碳的固溶强化三个因素的贡献。

3.TiB纤维由于其高的体积分数和长径比，能最大程度地传递载荷，对复合材料屈服强度的提高贡献最大。而TiC颗粒传递载荷的影响作用十分有限，其主要通过强化位错效应起作用。

[1] Zhao YQ. Study on High Temperature Alloys[J]. Titanium Industry Progress, 2001, 3(1): 33～39.

[2] Rosenberger A H, Madsen A, Ghonem H. Aging Effects on the Creep Behavior of the Near-alpha Titanium Alloy Ti-1100[J]. Journal of Materials Engineering and Performance, 1995, 4(2): 182～187.

[3] 曾立英,赵永庆,洪权,毛小南,戚运莲. 600℃高温钛合金的研发[J]. 钛工业进展, 2012, 29(5): 1～5.

[4] 崔文芳,洪权,等. 近α高温钛合金600℃蠕变变形机制的TEM研究[J]. 中国有色金属学报, 1998, (S2): 198～201.

[5] Lu WJ, Zhang D, Zhang XN, Wu RJ, Sakata T, Mori H. Microstructure and Tensile Properties of in Situ (TiB+TiC)/Ti6242(TiB:TiC=1:1) Composites Prepared by Common Casting Technique[J]. Materials Science & Engineering, A, 2001, 311(1～2): 142～150.

[6] Lu WJ, Zhang D, Zhang XN, Wu RJ, Sakata T, Mori H. HREM Study of TiB/Ti Interfaces in a TiB-TiC in Situ Composite[J]. Scripta Mater, 2001, 44(7): 1069～1075.

[7] 吕维洁,肖旅,等. 原位合成多元增强耐热钛基复合材料[C].第十三届全国钛及钛合金学术交流会,洛阳, 2008，9.

[8] 李军,杨绍利,吴恩辉,侯静,黄平. TiAl/Al2O3复合材料的原位合成与表征[J]. 材料科学与工程学报, 2015, 33(3):465～468.

[9] 吕维洁,张荻.原位合成钛基复合材料的制备、微观结构及力学性能[M].北京:高等教育出版社,2005,9:133～148.

[10] Guo XL, Wang LQ, Wang MM, Qin JN, Zhang D, Lu WJ. Effects of Degree of Deformation on the Microstructure, Mechanical Properties and Texture of Hybrid-reinforced Titanium Matrix Composites[J]. Acta Materialia, 2012, 60(s 6～7): 2656～2667.

[11] Cox H L. The Elasticity and Strength of Paper and Other Fibrous materials[J]. British Journal of Applied Physics, 1952, 3(3):72～79.

[12] Nardone V C, Prewo K M. On the Strength of Discontinuous Silicon Carbide Reinforced Aluminum Composite[J]. Scripta Metallurgica, 1986, 20(1):43～48.

[13] V. C. Nordone, K. M. Prewo.[J]. Scripta Metall. Mater, 1986,20: 43.

[14] Fukuda H, Chou T W. A probabilistic theory of the strength of Short-fibre Composites with Variable Fibre Length and Orientation[J]. Journal of Materials Science, 1982, 17(4):1003～1011.

[15] Kuhlmann-Wilsdorf D, Harrigan W C. New Developments and Applications in Composites: Proceedings of a Symposium[J]. Biometrical Journal, 1979, 35(8):933～947.

[16] Hashin Z, Rosen B W. The Elastic Moduli of Fiber-Reinforced Materials[J]. Journal of Applied Mechanics, 1964, 31(2).

[17] Xiao L, Lu W J, Qin J N, et al. Steady State Creep of in Situ TiB Plus La2O3Reinforced High Temperature Titanium Matrix Composite[J]. Materials Science & Engineering A, 2009, 499(1):500～506.

[18] 庄伟彬, 宗亚平, 等. 铁基复合材料碳化硅粒子混合尺寸增强作用机理[J]. 材料科学与工程学报, 2013, 31(1):1～5.

[19] Shi N, Wilner B, Arsenault R J. An FEM Study of the Plastic Deformation Process of Whisker Reinforced SiC/Al Composites [J]. Acta Metallurgica Et Materialia, 1992, 40(11): 2841～2854.

[20] Ramakrishnan N. An Analytical Study on Strengthening of Particulate Reinforced Metal Matrix Composites[J]. Acta Materialia, 1996, 44(1):69～77.

[21] Zhang Q, Chen D L. A Model for Predicting the Particle Size Dependence of the Low Cycle Fatigue Life in Discontinuously Reinforced MMCs[J]. Scripta Materialia, 2004, 51(9):863～867.

[22] Schulte K. Mechanical and physical behaviour of Metallic and Ceramic Composites[C]. 9th Risø International Symposium on Metallurgy and Materials Science. Edited by S.I. Andersen, H. Lilhølt and O.B. Pedersen. Risø National Laboratory, Roskilde, Denmark, 1988. ISBN 8[J]. Composites Science & Technology, 1989, 36(4):368～370.

[23] 刘冀念, 董蓉桦, 刘炎,刘永星. 高体积分数SiCp/7075Al复合材料的时效析出行为[J]. 材料科学与工程学报, 2016, 34(3): 357～361.

[24] Dieter G E, Bacon D J. Mechanical metallurgy[M]. McGraw-Hill, 1961.

[25] Budiman A S, Narayanan K R, Li N, et al. Plasticity Evolution in Nanoscale Cu/Nb Single-crystal Multilayers as Revealed by Synchrotron X-ray Microdiffraction[J]. Materials Science & Engineering A, 2015, 635(03):6～12.

[26] François D, Pineau A, Zaoui A. Mechanical Behaviour of Materials[J]. Solid Mechanics & Its Applications, 1995, 180(Jul):1298～1305.

[27] Taya M, Arsenault R J. Metal Matrix Composites: Thermomechanical Behavior[M]. Pergamon Press, 1989.

[28] L. M. Brown, W. M. Stobbs. The Work-hardening of Copper-silica v. Equilibrium Plastic Relaxation by Secondary Dislocations[J]. Philosophical Magazine A, 1976, 34(3):351～372.

[29] Huang J C, Ardell A J. Addition Rules and the Contribution of δ′ Precipitates to Strengthening of Aged AlLiCu Alloys[J]. Acta Metallurgica, 1988, 36(11):2995～3006.

[30] Zhu A, Gable B M, Shiflet G J, et al. Trace Element Effects on Precipitation in Al-Cu-Mg-(Ag, Si) Alloys: a Computational Analysis[J]. Acta Materialia, 2004, 52(12):3671～3679.

[31] Yuan S P, Liu G, Wang R H, et al. Coupling Effect of Multiple Precipitates on the Ductile Fracture of Aged Al-Mg-Si Alloys[J]. Scripta Materialia, 2007, 57(9):865～868.

[32] C. Schlesier, E. Nembach. Strengthening of Aluminium-lithium Alloys by Long-range Ordered δ′-precipitates[J]. Acta Metallurgica Et Materialia, 1995, 43(11):3983～3990.