行为轨迹时空聚类与分析*
2018-06-25秦昆王玉龙赵鹏祥徐雯婷徐源泉
秦昆,王玉龙,赵鹏祥,徐雯婷,徐源泉
① 武汉大学 遥感信息工程学院,武汉 430079;② 香港理工大学 土地测量及地理资讯学系,香港
与日俱增的浮动车数据(点)、GNSS(全球导航卫星系统)轨迹数据(线)及相关街道网络数据等,构成了蕴含着人们行为模式和活动规律的行为轨迹大数据。它们隐藏着具有强时空相关性的时空聚类模式,实际应用时往往需要高时效地挖掘出其中的时空聚类模式,并对其进行高性能求解。行为轨迹数据是人类活动的记录,与人文学和社会学问题密切相关,需要与社会因素进行关联分析。行为轨迹大数据的高性能时空聚类与社会分析是地理信息科学与工程领域迫切需要解决的关键科学问题。
安装了车载GNSS定位装置并行驶在城市主干道上的出租车或公交汽车记录的浮动车数据,是记录行为轨迹的重要数据源。除此以外,还有为特定研究目的而设计并采集的轨迹数据(私家车轨迹数据、特定志愿者的轨迹数据等),以及智能手机记载的轨迹数据等,可以统称为行为轨迹数据。对浮动车在其行驶过程中定期记录的车辆位置、方向和速度信息,利用地图匹配、路径推测等相关计算模型和算法进行处理,可以建立浮动车和相关轨迹的位置数据和城市道路在时间和空间上的关联关系,得到浮动车的车辆行驶速度以及道路的行车旅行时间等交通拥堵信息。行为轨迹数据具有时空相关性,表现为数据对象在邻近的空间位置或相近的时间里具有相似的特征。在对行为轨迹数据进行时空相关性分析的基础上,利用时空聚类方法可以挖掘出具有强时空相关性的时空聚类模式,从而进一步分析和挖掘人们的出行行为模式、热点区域[1]、异常模式[2]和拥堵模式[3]等规律性时空知识。
在城市交通规划与管理以及城市社会管理过程中,常常需要及时甚至是实时地得到所需要的时空规律知识。行为轨迹大数据的时空聚类挖掘方法必须适应快速处理的要求和大数据处理的考验。传统的时空聚类方法由于受到算法、计算环境以及时空数据本身特征等因素的影响,难以满足高性能快速处理的要求,难以及时发挥有效作用。因此,必须对其加以合理取舍和适应性改造,增强时空信息存取、处理、分析和挖掘的并行计算和弹性计算能力,使其符合高性能处理要求,以达到充分利用各种计算资源,实现行为轨迹大数据时空聚类的高性能求解,从而为城市交通管理和社会管理等提供高时效的规律性知识。
行为轨迹数据是人们行为活动的真实记录,与社会因素密切相关。通过行为轨迹大数据的分析和挖掘,可以发现一些隐含的行为模式和活动规律,从而发现和理解个体与环境及其他个体间的交互作用。通过分析行为轨迹数据的特性、时空聚类模式等与社会因素的关系,我们可以解释行为轨迹大数据及其活动模式的社会学发生机制,分析其与社会要素之间的关联关系,从而为城市交通管理及社会管理等提供辅助信息和决策支持,并为地理信息科学与技术在人文社会学领域的应用奠定基础。
1 行为轨迹聚类及高性能求解方法
1.1 行为轨迹时空聚类方法
本文提出了考虑时空相关性的行为轨迹时空聚类挖掘的思路,技术路线如图1所示。
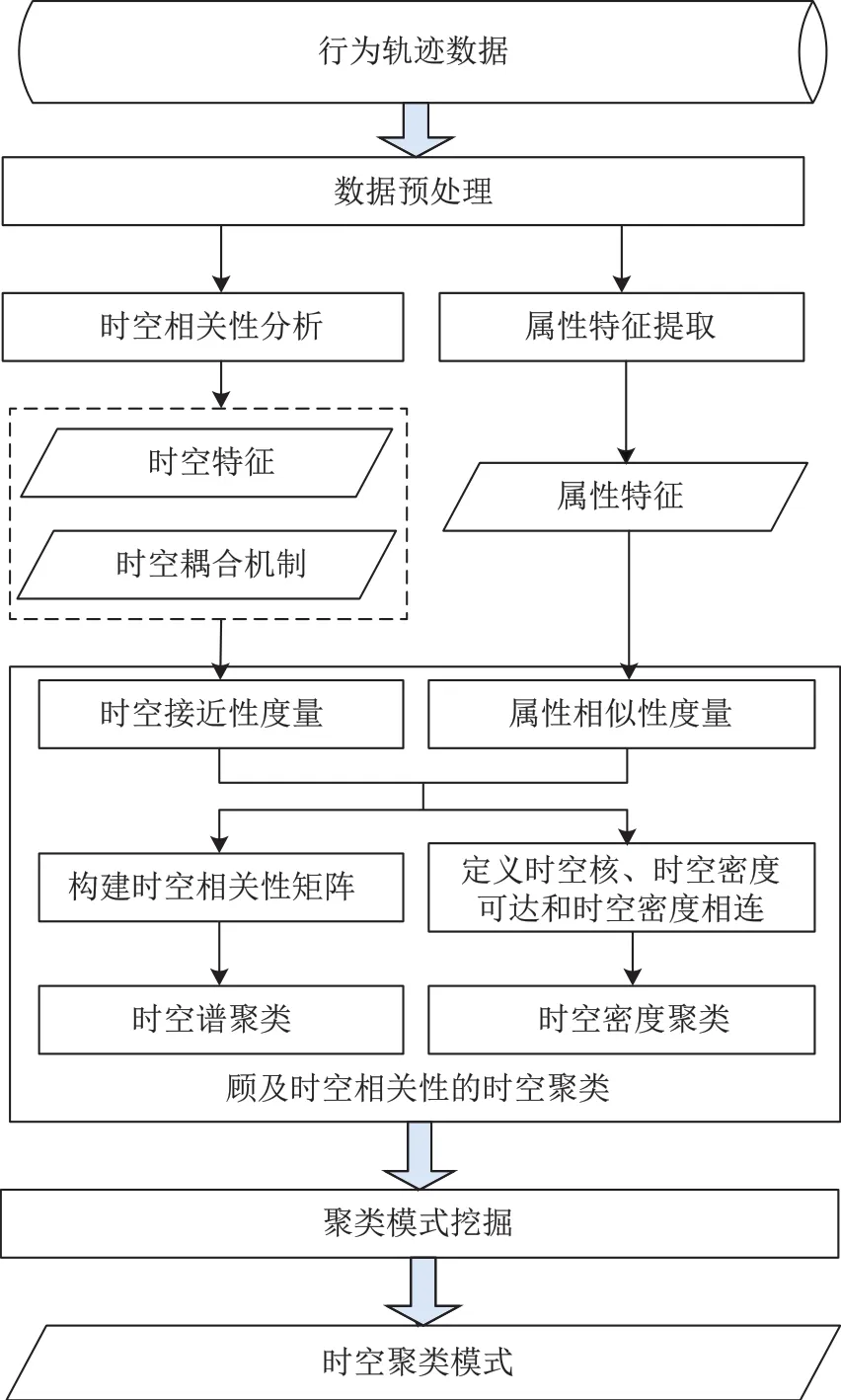
图1 行为轨迹时空聚类挖掘的技术路线
技术路线的具体描述如下:
(1)行为轨迹数据预处理:针对收集整理的行为轨迹数据,进行轨迹提取、噪声去除、轨迹分段等预处理,使得提取的每个轨迹线段成为相对独立的数据对象。
(2)时空相关性分析:从空间相关性、时间相关性和时空交互性等方面分析行为轨迹数据的时空相关性特征。
(3)属性特征提取:首先分析单个行为轨迹对象的属性特征,提取位置、运行速度、方向等属性特征,再进一步分析不同轨迹对象的时空相关性,提取与时空特性关联的属性特征。
(4)考虑时空相关性的时空聚类:考虑时空相关性,提出顾及时空相关性的时空聚类方法,主要包括时空谱聚类和时空密度聚类。这两种方法都同时考虑了轨迹数据的属性特征和时空相关性特征,对这两种特征分别进行相似性度量和接近性度量。
(5)时空聚类模式挖掘:利用时空聚类方法对行为轨迹数据进行时空聚类挖掘,挖掘其时空聚类模式,如客流热点区域、出租车接客模式、拥堵模式、出行模式等,并进一步考虑其时间特征,分析其时空演化模式。
1.2 行为轨迹时空聚类的高性能求解方法
行为轨迹时空聚类模型既是计算密集型的,也是数据密集型的,因此应分别从算法并行和数据并行两方面考虑,按照分布式数据库对数据并行的要求,研究行为轨迹的数据划分策略和弹性资源分配方法,按照高性能算法设计流程和方法,进行时空聚类算法的高性能优化求解。
我们团队提出了一种用于轨迹聚类的时空谱聚类并行化方法[4]。时空谱聚类算法是对传统谱聚类算法的时空扩展,运用到轨迹数据中时,容易遇到运算量过大的问题。一方面,轨迹数据本身的数据规模较大,对运算资源的要求较高;另一方面,谱聚类需要进行全局计算,计算复杂度较高,加入了时间因子后,计算复杂程度进一步提升,需要对算法进行高性能求解,以减少算法的运算时间。时空谱聚类算法的主要耗时操作为相似度矩阵的构建、拉普拉斯矩阵的构建以及拉普拉斯矩阵的特征值分解3个阶段。可以针对这3个阶段分别进行并行化计算。
相似度矩阵是一个n×n的矩阵,使用动态时间规整算法(DTW: dynamic time warping)来计算两点之间距离的复杂程度较高,因此当矩阵较大时,相似度矩阵的构建过程会消耗大量的时间。相似度矩阵中每一个元素值的计算过程都是独立的,每个元素值的计算不依赖其他元素值计算的结果,因此可以将这些计算过程进行并行化处理。传统的并行计算方法直接将矩阵连续几行的计算任务放入一个并行计算单元中,但是在对称矩阵的计算当中,由于每一行的计算任务数量不一,每一个并行单元的计算时间也不一样,主线程需要等待所有并行单元计算任务均执行完毕后才继续执行,而负载不均衡容易导致并行效率下降。因此,利用负载均衡的并行化策略对相似度矩阵的计算过程进行并行化。由于实现了各并行单元的负载均衡,总体的并行效率也会有相应的提升。拉普拉斯矩阵由相似度矩阵以及另一个矩阵(由度矩阵计算而来)相减得到,该计算过程实质上是两个矩阵对应值相减的过程,每个计算过程之间是独立的,可以将这些过程放到不同的并行单元中,实现并行化计算。
2 行为轨迹时空聚类的应用分析
2.1 热点区域提取
城市热点区域通常是指商业较发达、居民出行次数多和交通流量较大的区域,在某种程度上是人们密集出行的体现。出租车轨迹数据记录了车辆的日常运行轨迹,从轨迹数据中提取得到的上车点和下车点反映了乘客日常出行的出发地和目的地。因此,可以利用出租车轨迹进行城市热点区域提取,从而发现城市的活跃区域。
我们团队提出了一种利用决策图和数据场提取城市热点区域的方法[1]。首先将数据场的理论方法用于轨迹数据构建轨迹数据场,每个轨迹点可看作一个带有质量的粒子,其周围存在一个作用场,位于场中的任何轨迹点都将受到其他轨迹点的联合作用;其次,利用势熵法对参数σ进行优化选取,通过计算势熵来衡量势场分布的合理性,最终选取势熵最小的σ作为优化的影响因子;然后,利用决策图方法来选取聚类中心,聚类中心通常对应了势值的局部极大值点;最后,对去除噪声点之后的轨迹数据进行类的划分,将该数据对象与势值比其大且距其最近的数据对象划分到同一个类中,最终实现类的划分。
以武汉市2014年5月1日至10日的出租车轨迹数据为数据源进行城市热点提取的实验,轨迹数据的采样间隔为60 s。将每天的轨迹数据按小时划分为24个时段。分时段提取轨迹数据有助于分析各个时段内热点区域的动态变化。图2为工作日和周末的18:00~19:00时段内城市热点区域分布。结果表明:某些区域为持续性热点区域,总体上随时间变化较小,而另一些热点区域只在工作日或周末的个别时间段内出现。此外,在工作日,居民的出行多为“居住地—工作地”的通勤模式。在非工作日,多为“居住地—休闲地”或“休闲地间”的出行模式。因此,在非工作日,人们出行以及城市活动通常相对活跃,热点数量也较工作日多。
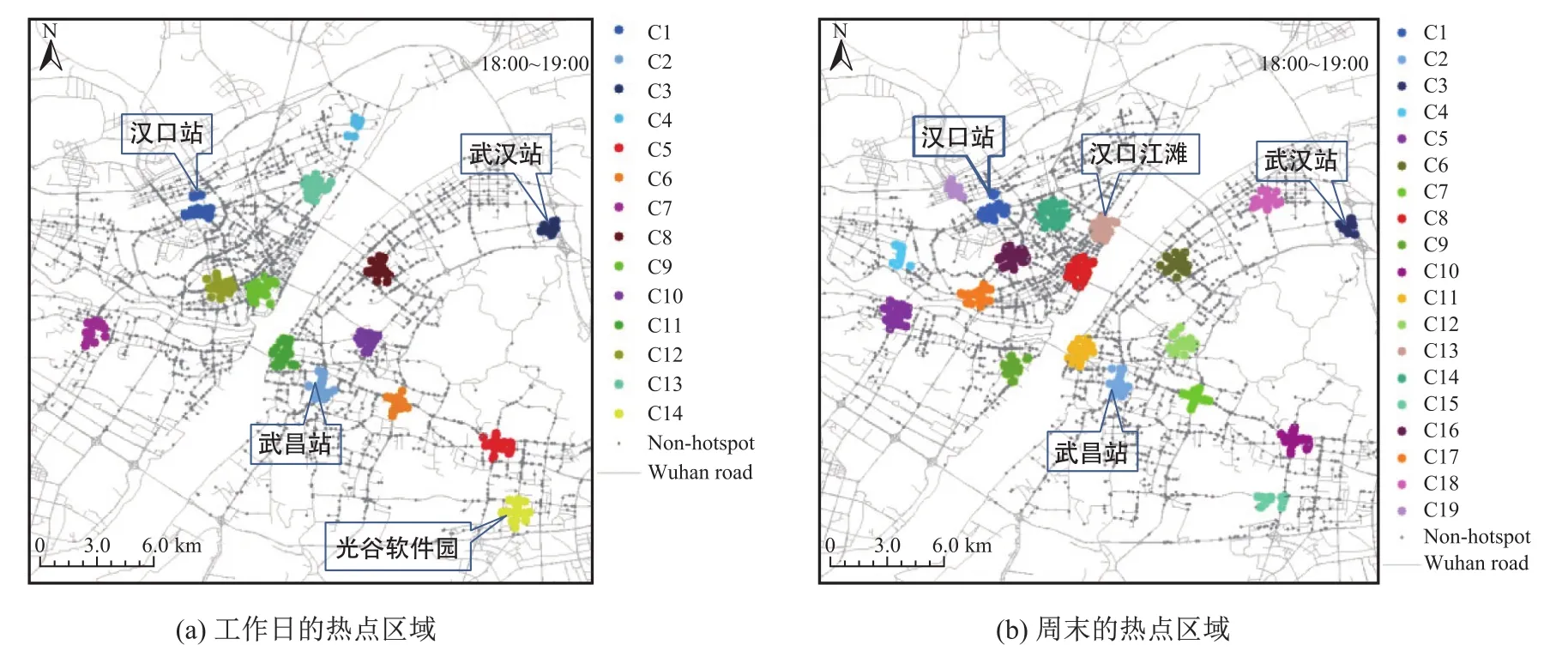
图2 工作日和周末18:00~19:00时段内的热点区域分布
2.2 异常轨迹探测
异常轨迹是指轨迹数据中不同于大多数驾驶者常规选择路线的轨迹。利用这些异常轨迹可以分析驾驶者或乘客的异常行为,可以为城市交通管理和社会管理等提供决策支持。轨迹聚类是异常轨迹探测的常用手段之一。利用轨迹聚类进行异常轨迹探测涉及两个关键问题:轨迹的相似性度量和自动确定合适的聚类数目。
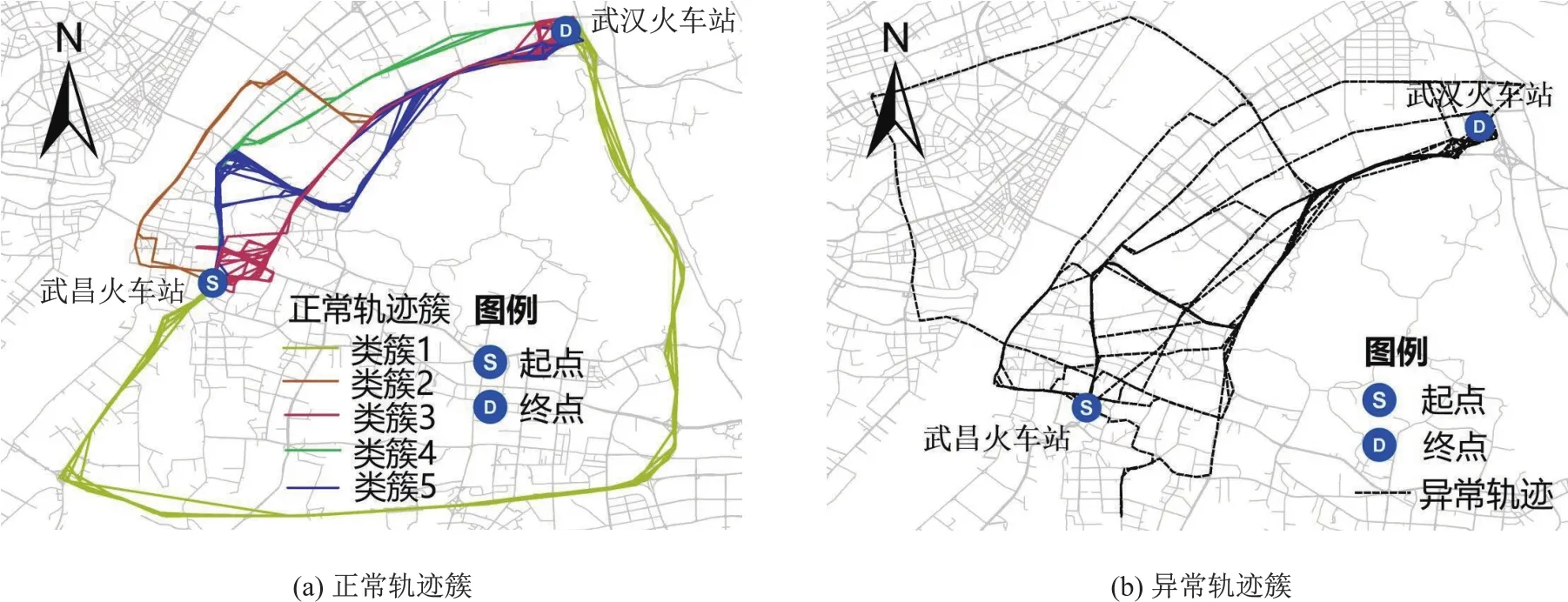
图3 出发地和目的地之间的正常轨迹聚类簇和异常轨迹簇
我们团队提出了一种基于编辑距离和层次聚类的异常轨迹探测方法[2]。利用编辑距离计算轨迹的相似性,利用一种编辑距离操作代价算法,使其适应轨迹数据连续记录的特点。利用基于层次聚类方法将轨迹数据聚类成不同的类簇,基于平方和指数自动确定聚类数目。
以武汉市2014年5月的出租车轨迹数据为数据源,选取武昌火车站为出发地,武汉火车站为目的地,获取它们之间的所有载客轨迹,利用异常轨迹探测方法进行实验,提取出发地和目的地之间的正常轨迹聚类簇和异常轨迹,如图3所示。
通过对异常轨迹与正常轨迹簇的时间和长度进行比较,并进一步推断可能的产生原因,异常轨迹可以划分为4种异常行为模式,具体包括:
(1)行为模式1:长度≤正常轨迹平均长度,时间≤正常轨迹平均时间。根据该行为模式推断:该轨迹可能是一个经验丰富的出租车司机凭经验选择的一条捷径。利用该方法可以自动发现一些最优路线。
(2)行为模式2:长度≤正常轨迹平均长度,时间>正常轨迹平均时间。根据该行为模式推断:可能遇到了拥堵、交通管制等特殊事件。利用该方法可以自动发现一些路段中可能存在的特殊事件。
(3)行为模式3:长度>正常轨迹平均长度,时间≤正常轨迹平均时间。根据该行为模式推断:可能是为了赶时间,为了避开拥堵区域,而选择了虽然路程较远,但是可以节约时间的路线。利用该方法可以自动发现一些可以节约时间的路线。
(4)行为模式4:长度>正常轨迹平均长度,时间>正常轨迹平均时间。根据该行为模式推断:可能是司机故意绕道。利用该方法可以自动发现一些可能的出租车司机故意绕道行为,从而为出租车管理提供一些参考。
2.3 交通拥堵分析
城市交通拥堵是指一定数量的车辆持续性缓慢行驶或停止所形成的聚集现象,可能是由城市车辆过多、道路结构不合理等因素造成。交通拥堵分析有助于了解道路状况,预测交通流量趋势,进而为交通管理、城市管理等提供决策支持。
我们团队提出了一种基于时间与空间相似性和相异性的时空密度聚类方法[3],该方法将传统空间轨迹点聚类扩展为时空轨迹段聚类,进而提取交通拥堵区域;然后运用 Ripley′s K 函数描述不同时段下城市拥堵的聚集性程度随距离的变化关系;基于轨迹数据场理论定量化探索不同时段下交通拥堵的强度分布。最后,通过对城市拥堵区域的形态进行时空分析,提出了11种城市拥堵区域的时空变化模式:新增模式、消散模式、分裂模式、合并模式、分裂合并模式、稳定模式、稳定移动模式、收缩模式、收缩移动模式、增长模式和增长移动模式等。
出租车轨迹数据是研究城市交通拥堵的重要数据源之一。以武汉市2014年5月1日、5月11日、5月13日的出租车轨迹数据(分别代表节假日、周末、工作日)为数据源进行实验,获取3种日期类型对应的城市拥堵区域及其分布模式。以5月13日(工作日)为例,结果如图4所示。
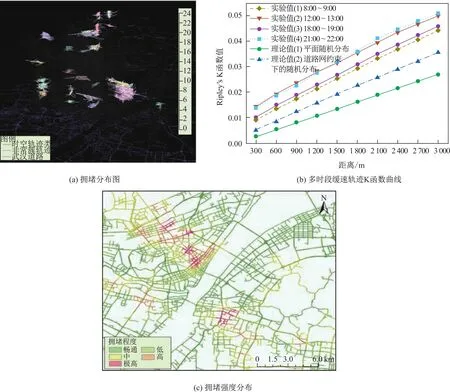
图4 交通拥堵分析(2014年5月13日)实验结果图
通过分析不同时期的城市拥堵分布结果,得到以下结论:①存在常发性拥堵区域,主要分布于车站、部分商圈与主干道附近,例如汉口火车站、解放大道、珞喻路和王家湾等区域。②一天内拥堵分布具有高低峰,高峰时段的拥堵空间跨度与类簇数量明显高于低峰时段。③不同日期的空间分布情况具有不同偏向,工作日多分布于行政工作区,周末更倾向于休闲娱乐区,而节假日明显聚集于旅游景点区。④拥堵在不同日期下的时间分布也不尽相同,节假日与休息日较为相似,拥堵的时间跨度在全天较为均匀,工作日则更为集中地分布在高峰时段,且拥堵强度也更为突出。这表明人们的出行时间在周末和节假日较为分散和自由,而在工作日的出行时间更为集中。⑤关于拥堵事件的发生,呈现显著的节假日>周末>工作日的特征。⑥缓速轨迹相较于一般轨迹在道路网上更为集中。⑦低峰时段K值高于高峰时段,表明低峰时的拥堵主要集中发生于少数特定路段,这使得整体聚集程度较高。
3 总结与展望
行为轨迹大数据的高性能时空聚类与社会分析是地理信息科学与工程领域迫切需要解决的关键科学问题。本文对行为轨迹时空聚类及其高性能求解的方法进行了探索,研究了行为轨迹时空聚类在热点区域提取、异常轨迹探测、交通拥堵分析等方面的应用,还需要将行为轨迹时空聚类结合社会地理计算、空间交互网络分析等进一步深入研究。
[1]ZHAO P X, QIN K, YE X Y, et al. A trajectory clustering approach based on decision graph and data field for detecting hotspots [J].International Journal of Geographical Information Science, 2017,31(6): 1101-1127.
[2]WANG Y L, QIN K, CHEN Y X, et al. Detecting anomalous trajectories and behavior patterns using hierarchical clustering from taxi GPS data [J]. ISPRS International Journal of Geo-Information,2018, 7(1): 1-20.
[3]LIU C K, QIN K , KANG C G. exploring time-dependent traffic congestion patterns from taxi trajectory data [C]//ICSDM 2015 -Proceedings 2015 2nd IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services, October 13, 2015,Fuzhou, China. 2015: 39-44.
[4]GU Y Z, QIN K, CHEN Y X, et al. Parallel spatiotemporal spectral clustering with massive trajectory data [C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science, Volume XLII-2/W7. ISPRS Geospatial Week 2017, 18-22 September 2017, Wuhan, China. 2017: 1173-1180.
