吸力锚下放过程的动力学分析
2018-06-23张大朋张霄杰许雨心朱克强
张大朋,张霄杰,许雨心,白 勇,朱克强,周 晨
1.浙江大学建工学院,浙江杭州 310058
2.南方科技大学海洋科学与工程系,广东深圳 518055
3.宁波大学海运学院,浙江宁波 315211
传统的带缆锚定系泊方式的局限性日益突出,由此吸力锚技术应运而生,它可为船舶平台提供系泊力和支撑基础,且施工较简便,可反复利用[1-2]。纵观国内相关文献,关于吸力锚的研究主要集中于吸力锚海上下放后,其自身与海床之间的接触力和吸力的变化情况,及海床在这个过程中的变形情况,而对于吸力锚本身下放过程的动态分析,则非常缺乏[3-7]。吸力锚在下放过程中,极有可能出现脱缆进而发生触底现象,或是与施工船舶发生剧烈碰撞的现象,这些现象会造成严重的施工事故。因此,有必要对吸力锚的下放过程进行分析。
本文依据某吸力锚具体下放过程,运用大型水动力软件OrcaFlex的时域耦合动力学分析法,建立了吸力锚下放过程的动力学分析模型。结合动力学仿真的结果,给出了一些建议,对具体工程实践有一定的指导意义。
1 基本理论
建立的吸力锚下放起重船坐标系及结构简图如图1所示,其中O0X0Y0Z0是惯性坐标系,Oxyz是船体坐标系。图1中,A点是吊臂的端点,P点是吸力锚简化后的质点,α和β分别表示面外摆角和面内摆角。
因下放系统吊缆的伸长量和弯扭刚度很小,故本文暂不考虑。吊缆处于张紧状态时可近似看成一根弹性杆件,故将吊缆离散成质量-弹簧模型,基于凝集质量法[8-14]分析得到其张力:
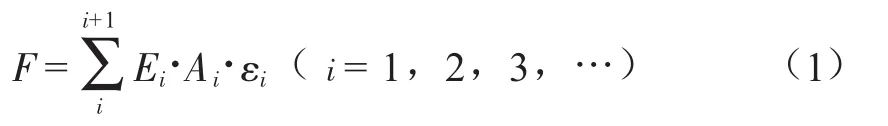
式中:F为吊缆处于张紧状态时的张力,kN;Ei为选定某段吊缆的弹性模量,kN/m2;Ai为选定某段吊缆的横截面积,m2;εi为纵向应变,无量纲。
则其有效张力为:

式中:为考虑水动力作用下的吊缆有效张力,kN;Fi为吊缆的张力,kN;FP表示呈阶梯状作用在吊缆上的静水压力,kN。
水动力可以由Morison方程计算得到

式中:Fd为水动力,kN;CA表示附加质量系数,无量纲;CM表示惯性力系数,无量纲;Cd表示拖曳力系数,无量纲;Vn表示垂直于吊索的海流速度,m/s;表示垂直于吊索的海流加速度,m/s2;表示吊缆下降的速度,m/s;表示吊缆下降的加速度,m/s2。
故吊缆的运动方程

式中:ρ表示吊缆密度,kg/m;ρw表示海水密度,kg/m3;EI表示弯曲刚度,kN·m2;r¨为某一时刻吊缆的加速度,m/s2;r为某一时刻吊缆的位移,m;w表示有效质量,kg;上角标的撇号表示求导;k表示吊索曲率,rad/m。
令X(z,t)表示吊缆垂向位移(计量单位m),其中t表示时间(计量单位s),z为此时吊缆连接吸力锚一端的垂向位置(计量单位m)。为方便表达,缆索切向的拖曳力暂不考虑,故在吊索张紧时其垂向的运动方程为:
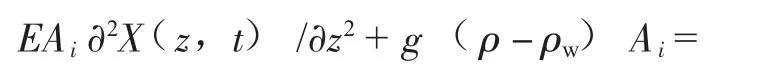

式中:E为弹性模量,kN/m2;g为重力加速度,m/s2,取9.8;m为单位长度的质量,kg/m。
令v2=EAi/m
K=g( ρ- ρw) Ai/m
又EAi=mv2
代入上式整理得:
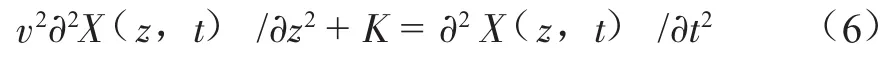
由船体的运动可知:

式中:v表示吊索内声音传播的速度,m/s;x表示船体的位移(包含6个自由度),平动时的计量单位是m,转动时的计量单位是rad;R为船体响应幅值算子,对于平动其计量单位为m,对于转动其计量单位为rad;a表示波浪的幅值,m;ω表示波浪的圆频率,Hz;φ为船体初始相位角,rad。
令A点在船体坐标系内的初值为(xc,yc,zc),易得A点的运动方程为:
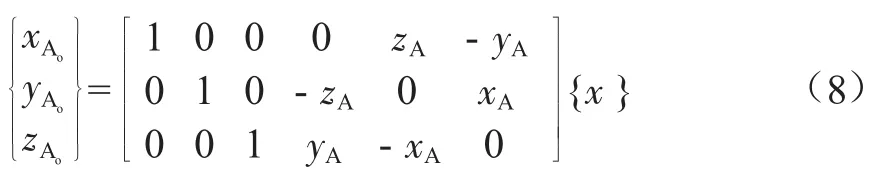
由此可得A点加速度:
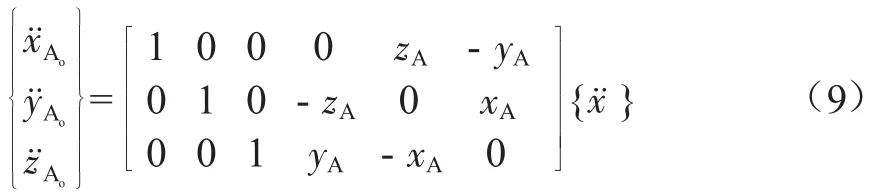
再由坐标轴之间的位置关系,可推导出A点在O0X0Y0Z0惯性坐标系内的坐标:


令l为吊缆总长(计量单位m),则吸力锚P的坐标为:
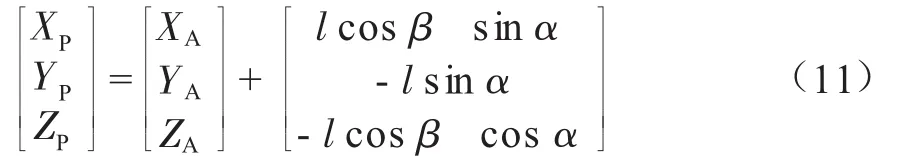
式中:XP,YP,ZP分别表示吸力锚的三个空间坐标值,m;α,β为吊缆首尾端在空间的摆角,计量单位是rad。
吸力锚在下放的过程中,由牛顿第二定律可知:

式中:GP表示吸力锚自身重力,kN;mP为吸力锚质量,kg;a是吸力锚的加速度,m/s2。
将吸力锚的受力投影到x、y、z轴各个方向上,A为吸力锚受阻面积,则(11)式可写成:

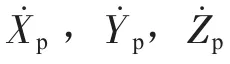
联立公式(1)~(13)即可求得吸力锚的面内摆角和吊索的有效张力。
2 OrcaFlex中模型的建立
本模型中下放吊缆运用Line模块进行构建,吸力锚运用6D浮标的Towed Fish子模块进行构建,通过赋予其相应的与吸力锚一致的水动力参数、质量和外在几何尺寸及转动惯量等力学性能参数,使其拥有与吸力锚相同的力学与水动力学性能;下放起重船运用软件中的Vessel单元进行构建,起重船的吊臂运用6D浮标中的凝集质量块单元构建,且为了实现吊臂的回转,吊臂和基座之间用4根弯曲刚度和扭转刚度极大的Line单元固结在一起,以保证吊臂随着基座的转动而转动。吸力锚垂直方向的下放通过在吊缆上端连接Winch单元实现,通过控制Winch单元的伸缩,实现吸力锚的下放;在仿真的最初始阶段,用两个水平布置的Winch单元将吸力锚水平向船尾方向横推,使得吸力锚在初始阶段迅速脱离起重船,此阶段结束后两个水平布置的Winch迅速脱离,不再发挥作用,此后阶段通过与吊缆上端相连的Winch单元来控制吸力锚的垂直下放,下放速度为0.1 m/s。
为尽量保证模拟的真实程度,用4个起弹簧阻尼器作用的Link单元将6D浮标模拟的吸力锚与3D浮标模拟的缆扣相连,因为在OrcaFlex中Link的作用相当于一个弹簧阻尼器,可以轴向伸缩,这样可以缓冲吸力锚下放在模拟过程中的冲击,以保证系统整体的运动性能。然后再将吊缆的下端与缆扣相连。吊缆的轴向刚度EA为236 kN,泊松比υ为0.5,长度为50 m,直径d为0.055 m。吸力锚质量为190 t,几何外形为长3 m、外径为5 m、内径为4.9 m的中空圆柱体,其中在圆柱体的最顶端0.05 m长度范围内其为一小段外径为5 m、内径为0的实心小圆柱,吸力锚的转动惯量Ix=Iy=14 844 t·m2,Iz=1 187.5 t·m2,吸力锚的拖曳力系数和惯性力系数按照其给出的真实值进行取值,因其数值在吸力锚长度方向上分段分布,较为繁琐,这里不再列出。
常见的操作工况为顺浪方向,最危险的操作工况为横浪向,因此这里取这两种典型的工况进行分析,其中顺浪向为浪向为0°时,横浪向为浪向为90°时。模型建成后如图2所示。因在各种波浪理论中,斯托克斯五阶波理论计算结果较为保守,且在工程中多运用斯托克斯五阶波,因此这里计算波浪理论选取斯托克斯五阶波,波高取0.2 m,波浪周期取7 s,水深为500 m。

图2 在OrcaFlex中建立的吸力锚下放模型
3 计算结果
3.1 顺浪向下放过程的动力学分析
图3~5为吸力锚顺浪向下放过程中张力、质心位置和吸力锚干长度变化图像,对比发现:在吸力锚完全没入海水中之前,吊缆张力在时域上近似呈现线性降低的趋势,而在吸力锚完全没入海水中之后,波浪对于吸力锚的水动力载荷对于吊缆的张力影响较大,吊缆张力幅值开始在时域上发生急剧的高频波动。
图6~8为顺浪向时吸力锚的横摇角、纵摇角和艏摇角的变化。
对比观察图5和图7发现:在吸力锚完全没入水中之前,吸力锚纵摇角在时域上变化较小,近似为0°,而当吸力锚完全没入水中之后,吸力锚在时域范围内开始发生较大范围的波动。需要指出的是,其中横摇是指绕着吸力锚纵向中轴线(定义为z轴)方向的转动,纵摇是指绕着与纵向中轴线垂直的直线(定义为x轴)转动,艏摇是指绕着与纵向中轴线垂直的另一条直线(定义为y轴)转动,其中,x轴和y轴在吸力锚横截面形心相交,交点为o,且x轴与y轴也相互垂直。
观察图6与图8发现,在整个下放的过程中吸力锚的横摇角及艏摇角均为0°,没有随着吸力锚下放位置的不同及吸力锚干长度的变化而变化。
综上所述,在顺浪状态下,吸力锚下放的过程中不会发生大范围的横摇及艏摇,但在吸力锚完全没入水中后会发生比较明显的纵摇。以吸力锚是否完全没入水中为界限,整个过程可以划分为两个比较明显的阶段,即在吸力锚未完全没入水中时的阶段和吸力锚完全没入水中的阶段。在第一个阶段吊缆张力在时域上近似呈现线性降低,吸力锚纵摇角在时域上有极小范围波动,在第二个阶段吊缆张力和吸力锚纵摇角都会在时域上发生幅值较大的急剧高频波动。

图3 顺浪向下放吊缆张力

图4 顺浪向下放锚质心位置

图5 顺浪向下放吸力锚干长度时域图
3.2 横浪向下放过程的动力学分析

图6 顺浪向下放吸力锚横摇角时域图
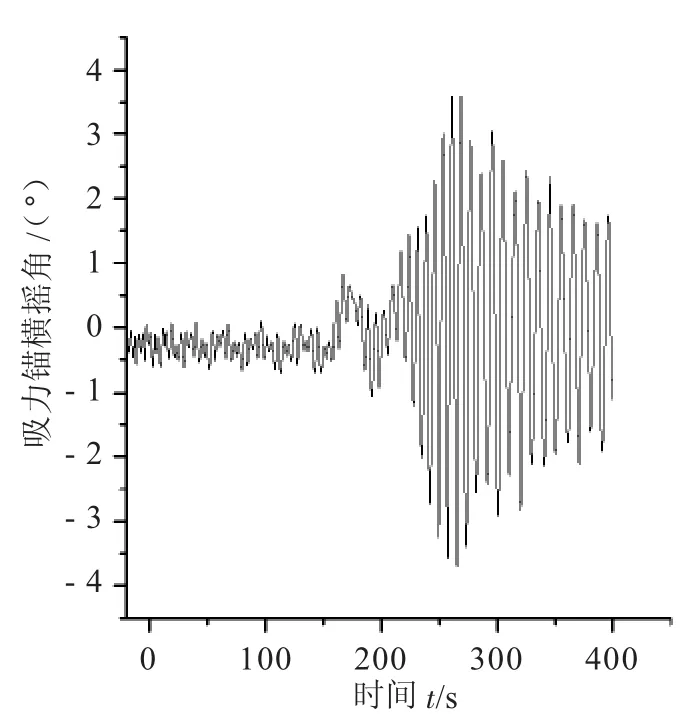
图7 顺浪向下放吸力锚纵摇角时域图

图8 顺浪向下放吸力锚艏摇角时域图
将横浪状态下的吸力锚下放计算结果(见图9~14)与顺浪状态下的进行对比发现:主要的不同集中在吸力锚横摇角和艏摇角方面,在顺浪状态下吸力锚的横摇角和艏摇角始终为0°,而在横浪状态下,吸力锚的横摇角在时域上随着吸力锚入水深度的增加其横摇值也逐渐增加,艏摇角则呈现出在时域上先增大后减小并会在时域中发生小范围的反复波动。产生这种现象的原因为,在横浪状态下,吸力锚的迎浪面积增大,波浪直接作用于吸力锚,且随着过程的继续,吸力锚入水深度逐渐增加,因而迎浪面积持续增大,进而在横摇方向受到的水动力持续增大,进而导致横摇角持续增大;而横摇角发生变化后,吸力锚空间姿态不再垂直于海平面,加上吊缆张力的作用,会使吸力锚受到一个绕吸力锚中轴的扭转作用,因吊缆张力及吸力锚姿态不断变化,因而扭转作用也不断变化,这也就使得吸力锚的横摇角在时域上会发生反复的波动。

图9 横浪向下放吊缆张力
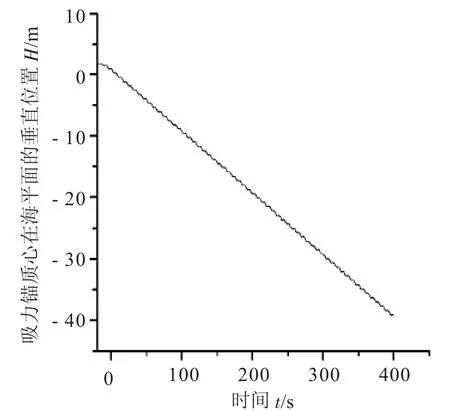
图10 横浪向下放锚质心位置
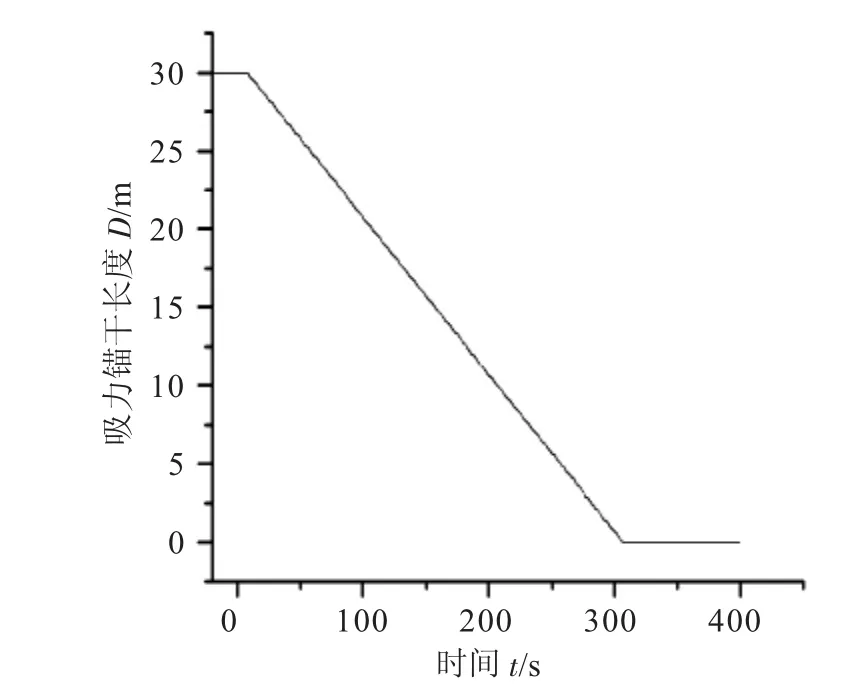
图11 横浪向下放吸力锚干长度时域图

图12 横浪向下放吸力锚横摇角时域图

图13 横浪向下放吸力锚纵摇角时域图

图14 横浪向下放吸力锚艏摇角时域图
4 结论
综上所述,在顺浪状态下,吸力锚下放的过程中不会发生大范围的横摇及艏摇,但在吸力锚完全没入水中后会发生比较明显的纵摇。以吸力锚是否完全没入水中为界限,整个过程可以划分为两个比较明显的阶段,即在吸力锚未完全没入水中时的阶段和吸力锚完全没入水中的阶段。在第一个阶段吊缆张力在时域上近似呈现线性降低,吸力锚纵摇角在时域上有极小范围波动,在第二个阶段吊缆张力和吸力锚纵摇角都会在时域上发生幅值较大的急剧高频波动。
横浪状态下的吸力锚下放计算结果与顺浪状态下的主要不同集中在吸力锚横摇角和艏摇角方面。在顺浪状态下吸力锚的横摇角和艏摇角始终为0°,而在横浪状态下,吸力锚的横摇角在时域上随着吸力锚入水深度的增加其横摇值也逐渐增加,艏摇角则呈现出在时域上先增大后减小并会在时域中发生小范围的反复波动。
[1]刁景华.吸力锚及其在海军工程中的应用[J].海军工程技术,2003(3):25-28.
[2]张秀林,王春波,尹彦坤.筒形基础海上安装方案探讨[J].中国海洋平台,2012,27(2):16-19.
[3]国振,王立忠,李玲玲.新型深水系泊基础研究进展[J].岩土力学,2011,32(S2):469-477.
[4]李洪江,刘红军,张浩.海上风力发电伞式吸力锚基础承载规律试验分析[J].水利学报,2015,46(12):1 460-1 469.
[5]刘晶磊,王建华.软土中张紧式吸力锚破坏标准模型试验与有限元分析[J].岩土力学,2013,34(9):2 508-2 514.
[6]丁红岩,刘振勇,陈星.吸力锚土塞在粉质粘土中形成的模型试验研究[J].岩土工程学报,2001(4):441-444.
[7]国振,王立忠.吸力锚基础锚泊线准静力分析模型[J].海洋工程,2009,27(4):1-9.
[8]朱克强,李道根,李维扬.海洋缆体系统的统一凝集参数时域分析法[J].海洋工程,2002,20(2):100-104.
[9]YANG Bingka,ZHU Keqiang,HU Yanjie,etal.Dynamic response of towed line array[J].Journal of Hydrodynamics,Ser.B.2013,25(4):616-619.
[10]朱艳杰,朱克强,杨冰卡,等.基于凝集质量法的海洋缆索动力学建模与仿真技术[J].海洋工程,2014,32(1):112-116.
[11]张大朋,朱克强.不同浪向下大型回转式起重船回转起吊作业过程的动力学分析[J].中国海洋大学学报(自然科学版),2017,47(5):128-134.
[12]张大朋,朱克强,李园园,等.波流联合作用下多分枝拖曳线列阵回转过程的动力学分析[J].船舶工程,2015,37(11):86-92.
[13]张大朋,朱克强,荆彪,等.文昌脐带缆J型牵拉入位操作的水动力分析[J].船舶工程,2015,37(4):92-97.
[14]张大朋,朱克强,李园园,等.不同Munk矩系数作用下海洋拖曳系统水动力响应分析[J].船舶工程,2016,38(4):86-90.
