大型地下工程围岩力学参数反分析方法研究

张与馨，黄 端

(重庆交通大学河海学院，重庆400074)

0 引 言

地下工程能够拓展工程布置范围，提高地下空间资源的利用率，正逐渐成为水电站厂房布置的首选。自上而下分层式开挖支护施工以及周围地质条件变化，均会引起地下工程围岩产生相应的力学响应(如松弛深度、围岩变形等)，有必要根据施工过程中实时获取的围岩力学参数，评判地下工程的安全性。基于地下工程现场监测资料的位移反分析是获得岩体力学参数的一种有效方法，国内许多学者已针对该理论做了广泛研究。倪绍虎等[1-2]利用粒子群优化算法(PSO)提高了地下工程围岩力学参数反演分析的效率；江权等[3- 4]基于遗传算法和前馈神经网络相结合的智能进化算法，对地下工程等效力学参数进行反演；王复明等[5]在围岩力学参数反演分析过程中引入了小波支持向量机理论。

上述研究成果虽然对智能位移反分析方法做了大量研究及改进，但反演结果仍存在着收敛性慢、稳定性差、泛化能力低等缺陷。鉴此，本文将小波理论和BP神经网络相结合形成的小波神经网络算法以及均匀设计理论应用到我国某在建水电站大型地下工程洞室力学参数反演分析中，以期优化地下工程位移反分析的速度和准确性。

1 理论基础

1.1 均匀设计理论

均匀设计理论(Uniform Design Experimentation)强调试验数据在边界条件内部分散的均匀性和一致性，是多因素多水平试验经常采用的一种数论方法。在基于均匀设计理念确定待试验组合方案时，首先需要借助均匀设计表，均匀设计表一般用Un(qs)表示，U为均匀设计；n为表的行数，即试验的水平数(试验次数)；q为每个因素的水平数(则n=q)；s为表的列数。若将Un(qs)中各列水平数组成1个q×s的矩阵，可以得到该矩阵的秩r≤s/2+1。在考虑到试验影响因素相关性的前提下，表Un(qs)安排的试验因素个数不能多于s/2+1[6]。均匀设计表在使用时都要查询与之匹配的使用表来安排试验。利用均匀设计理论的本质可以对模型未知的岩土工程问题进行优化设计。

1.2 小波神经网络理论

1.2.1 小波理论

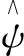
1.2.2 小波神经网络

小波神经网络做为一种前沿的高效数据建模和分析理论，与传统BP神经网络的相同之处为二者的网络结构和数学表达式基本一致，小波网络结构由输入层、隐含层和输出层组成(见图1)。2种网络的主要区别在于传统BP神经网络采用Sigomoid函数作为隐含层的激励函数；而小波神经网络采用离散小波基函数ψ(t)，更具有较强的容错和逼近能力[8]。2种网络输出层的激励函数均取Sigomoid函数。

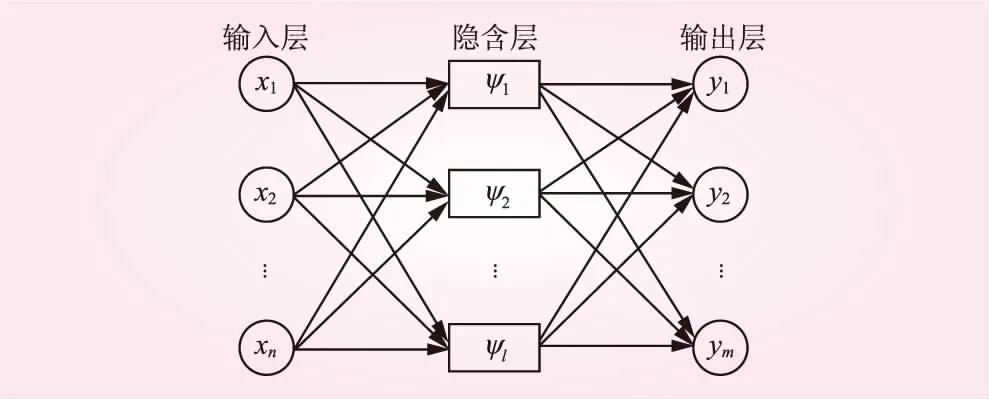
图1 小波神经网络结构

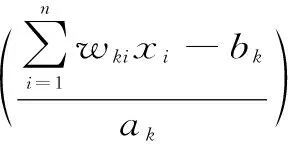
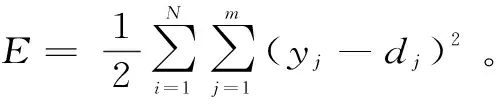
1.2.3 小波神经网络算法步骤

初始化网络参数包括设置权重wij和wjk、隐含层激励函数中的平移变量ak以及伸缩变量bk、隐含层神经单元数量l、学习率η、动量修正系数u、允许误差ε以及最大训练次数M。其中，wij、wjk、ak、bk为随机值。网络训练流程见图2。

图2 网络训练流程

2 基本原理及操作流程

2.1 基本原理

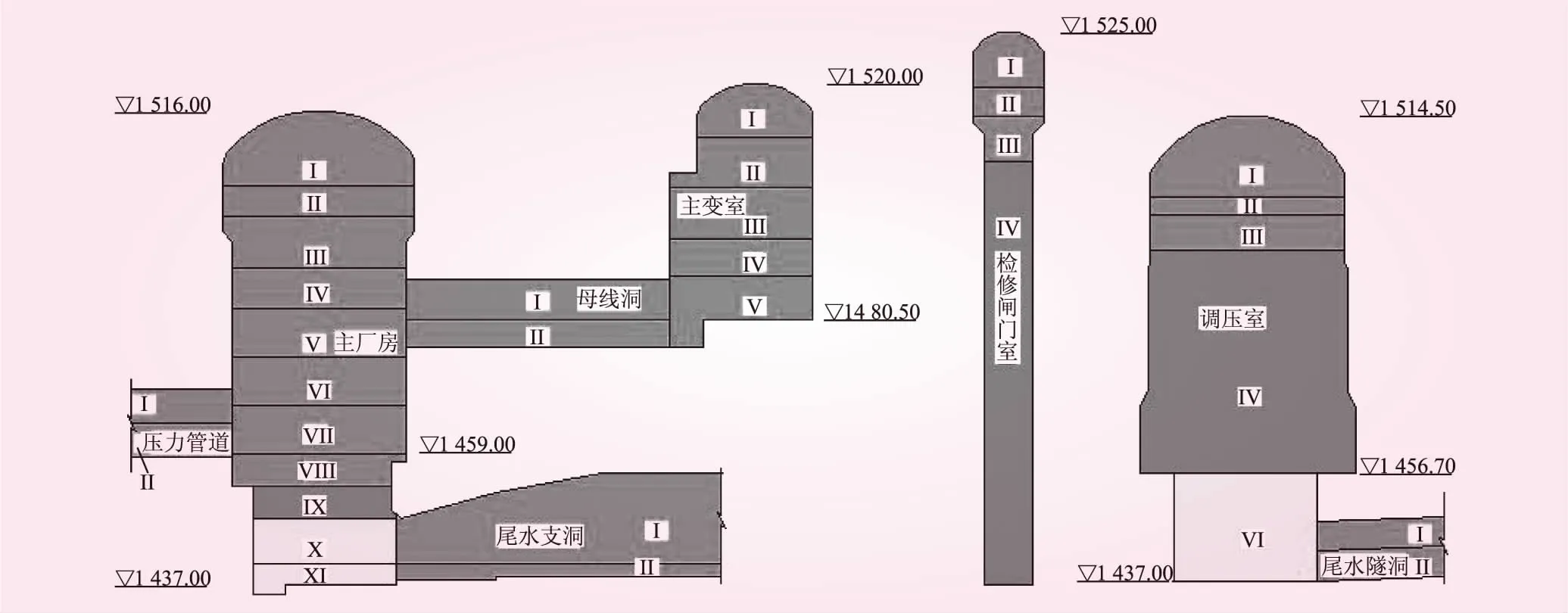
图3 地下洞室开挖分层步序(高程：m)

地下工程围岩力学参数反分析是指以现场实时监测资料为基础，通过反演模型反求厂区岩体力学参数的一种理论方法。鉴于在地下洞室实际施工过程中，位移监测比应力监测更经济方便，因此目前地下工程中位移反分析理论被广泛采用。位移反分析又可分为正反分析和逆反分析，前者能够同时适用于求解线性及非线性问题；后者通过逐次修正可调参数的取值来逼近实测数据，工作量大，耗时多，因此前者运用最为广泛，通常也称为位移优化反演分析法。为简化问题，进行位移优化反演分析的前提是通常假定岩体是均质、各向同性的，工程影响范围内的初始地应力场也是均匀的，即采用均质各向同性的连续体模型和固定初始地应力的边界条件，反演所得到的参数是在综合考虑了岩体节理、岩层等不连续面及各种地质工程因素的情形下计算的，因此这些参数又被称为等效岩体力学参数[10]，得到的参数不能同室内或野外试验所得到的结果进行比较，仅用于在同等条件下的工程预测和安全评价。随着地下工程的逐步开挖，实时更新的监测位移资料可以被用来进行新一轮的岩石力学参数反演，并用反演结果进行实时工程评价和预测，为工程设计和施工支护提供决策依据。

2.2 操作流程

基于均匀设计理论及小波神经网络人工智能算法的大型地下工程位移反分析的具体操作流程如下：

(1)建立大型地下工程三维全尺度施工数值仿真有限元计算模型。

(2)根据地质勘察资料和室内外岩石力学性质试验确定围岩力学参数的取值范围。

(3)针对每个待反演参数，在其取值范围内均匀选取N个值，然后利用均匀试验设计理论确定出N组不同的参数组合。

(4)分别针对每组参数组合进行有限元计算，提取三维计算模型中监测特征点的位移，从而形成小波神经网络训练样本集。

(5)利用小波神经网络非线性映射系统模型确定待反演力学参数与监测特征点有限元计算位移值之间的定量特征关系表达式。

(6)将地下工程现场监测特征点的最新监测位移代入已训练好的小波神经网络中，从而计算出待反演参数。

(7)将模拟解析出的围岩力学参数代入模型中进行有限元分析，计算相应测点的位移值，将监测特征点的计算位移与实际量测位移进行比较分析，评判反演参数的精确度。

(8)若不满足精度要求，调整参数取值范围，重复(2)～(7)步骤，直至满足精度要求为止。

3 工程实例

本文利用我国西南地区某在建水电站大型地下工程第五期(即主厂房第Ⅴ层和主变室第Ⅴ层开挖)开挖完成后监测特征点的增量位移[11]进行围岩力学参数反分析。图3为该地下工程具体的开挖分层步序。该地下工程地段岩体以II、III类围岩为主，完整性较好；局部区域分布有少量岩性较差的IV类岩体。围岩物理力学参数见表1。

表1 围岩物理力学参数

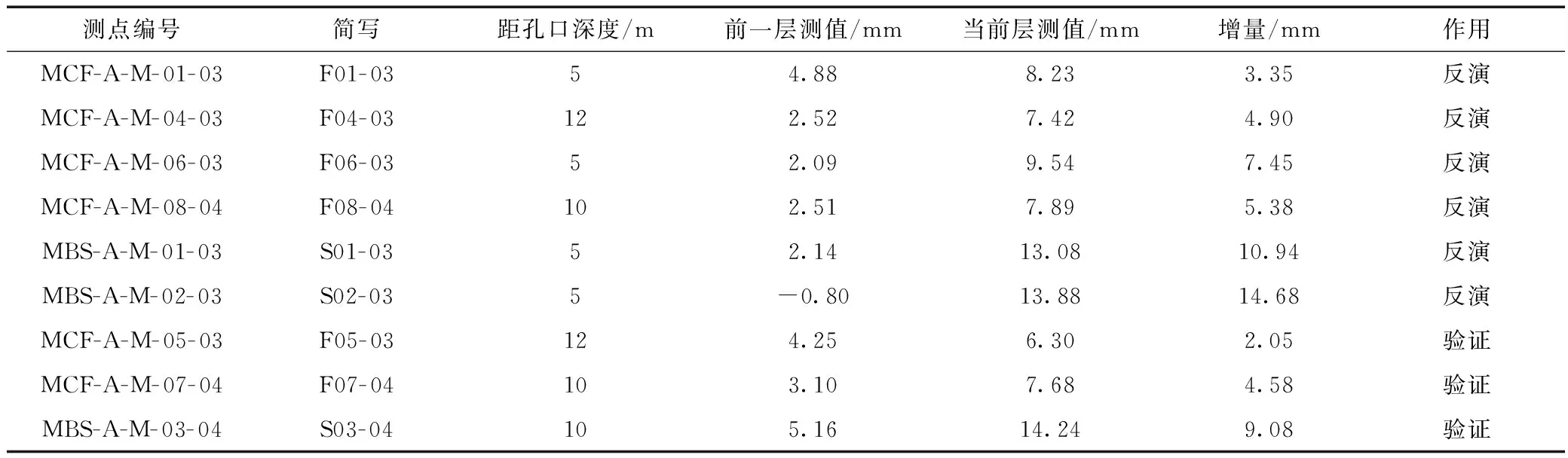
表2 测点监测位移

3.1 模型建立

三维有限元计算模型共剖分单元315 707个，节点69 117个。三维有限元计算模型网格见图4。

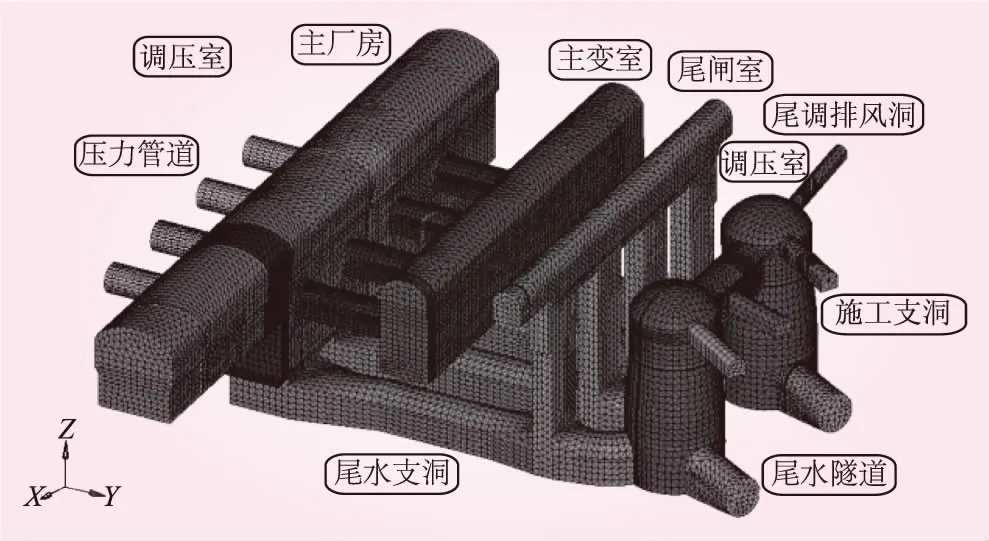
图4 地下洞室开挖单元计算模型网格

3.2 确定监测特征点

为使反演结果能代表整个地下工程岩体的力学性质，同时遵循大值原则和敏感性原则[12]，选取 0+105.000监测断面不同部位(拱顶、拱座、边墙)

的位移监测数据用于本次分析。多点位移计布置见图5。表2为相对应测点的位移监测数据。

图5 多点位移计布置(高程：m)

3.3 构造训练样本

位移反分析理论通常将岩体的待反演物理力学参数分为强度特性参数(包括内摩擦角φ和粘聚力с)和变形特性参数(包括变形模量E和泊松比μ)。φ、с、μ对围岩变形影响较小，为简化反演过程，这3个参数取建议值，仅将E作为反分析过程中的待反演参数[13]，II、III、IV类围岩的弹性模量分别为E2、E3、E4。利用U25(259)确定待反演参数样本，将样本中的力学参数组合分别输入到有限元计算模型进行分析求解，得到特征点处的增量位移计算值，由参数组合及其相应的计算值共同组成训练样本，见表3。表中的前20组样本用于网络训练，后5组样本用于网络验证。

3.4 神经网络训练

分别选取Sigomoid函数和小波函数f(x)=cos(1.75x)e(-x2/2)作为隐含层的激励函数[14]，建立传统BP神经网络和小波神经网络用于该地下工程的位移反分析。隐含层包含6个神经元。传统BP神经网络经过5 358次迭代计算后的网络总体误差趋于稳定，网络训练完成。而小波神经网络仅经过2 502次迭代计算就可以完成训练。将表2中原始监测位移数据分别导入到这2种网络中，反演计算得到的围岩物理等效力学参数见表4。

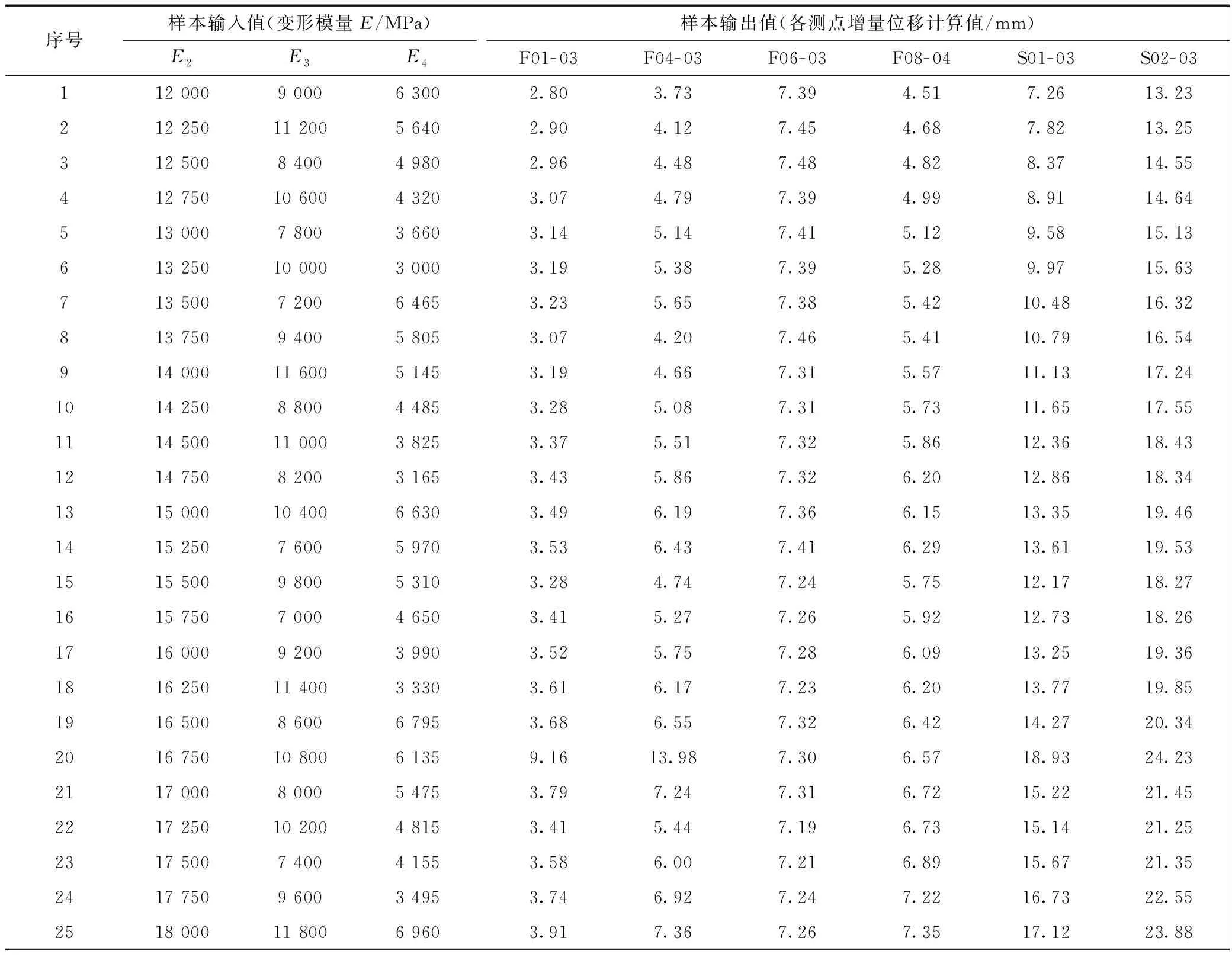
表3 网络训练样本

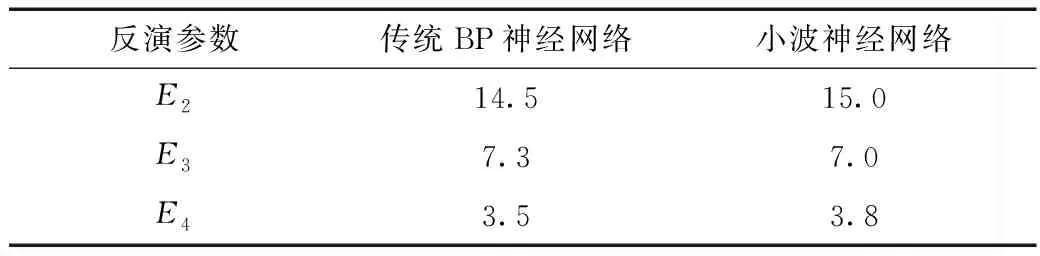
表4 反演参数计算结果 GPa

表5 测点位移增量计算值与实测值对比

3.5 反分析结果检验

将反演得到的岩体力学参数重新输入计算模型进行有限元正分析，对参与反演和检验的各测点计算结果与实测值(增量位移)进行对比分析，验证结果见表5。绝对误差对比分析见图6。

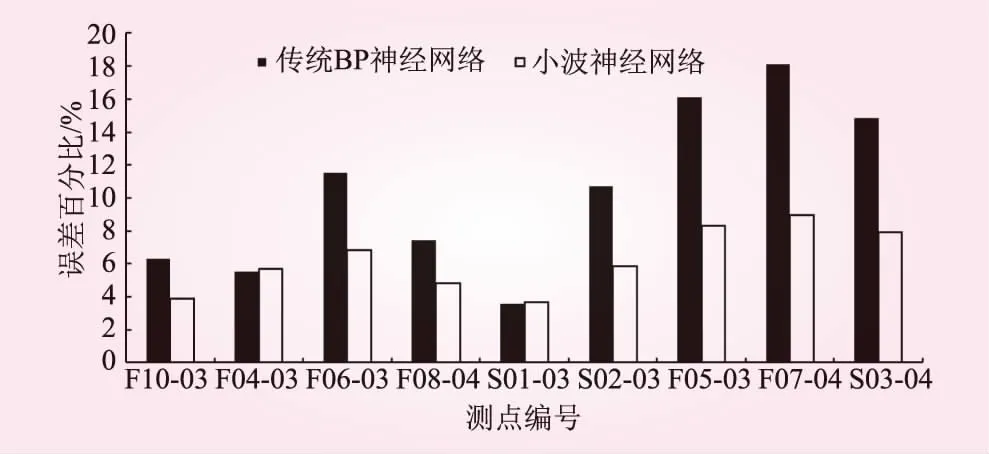
图6 绝对误差对比分析

由以上分析可知，在同等条件下，与传统BP神经网络作为位移反分析的人工智能算法相比，利用小波神经网络反演得到的该地下工程围岩等效力学参数更加有效、合格，可用于后期的安全评价和工程设计。

4 结 语

小波神经网络由于集合了小波理论与传统BP神经网络各自的优点，因此其非线性映射系统具有收敛快、稳定性强、泛化能力高等优势。将均匀设计理论和小波神经网络用于某大型地下工程第五期围岩力学参数反分析，在保证样本均匀性的同时，在很大程度上减少了网络学习的样本数量，且在反演具体流程中将有限元正分析与反分析相分离，可优化反分析的效率和精度。

[1] 倪绍虎, 肖明, 何世海, 等. 地下工程并行优化反演分析及算例验证[J]. 岩石力学与工程学报, 2013, 32(3)： 501- 511．

[2] 倪绍虎, 肖明. 基于围岩松动圈的地下工程参数场位移反分析[J]. 岩石力学与工程学报, 2009, 28(7)： 1439- 1446．

[3] 江权, 冯夏庭, 向天兵, 等. 大型洞室群稳定性分析与智能动态优化设计的数值仿真研究[J]. 岩石力学与工程学报, 2011, 30(3)： 524- 539．

[4] 江权, 侯靖, 冯夏庭, 等. 锦屏二级水电站地下厂房围岩局部不稳定问题的实时动态反馈分析与工程调控研究[J]. 岩石力学与工程学报, 2008, 27(9)： 1899- 1907．

[5] 王复明, 李晓龙, 苗丽, 等. 基于小波支持向量机的围岩力学参数辨识[J]. 水力发电学报, 2010, 29(3)： 184- 190．

[6] 李端有, 甘孝清, 周武. 基于均匀设计及遗传神经网络的大坝力学参数反分析方法[J]. 岩土工程学报, 2007, 29(1)： 125- 130．

[7] 谢成俊. 小波分析理论及工程应用[M]. 长春： 东北师范大学出版社, 2015．

[8] ZHANG J, WALTER G G, MIAO Y, et al. Wavelet neural networks for function learning[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1485- 1497．

[9] 高琳, 孙海蓉, 杨怀申. 一种结合PSO及改进BP网络的辨识方法[J]. 计算机工程与应用, 2010, 46(21)： 37- 39, 62．

[10] 高谦, 薛改利, 杨志强, 等.等效岩体力学参数识别及边坡稳定性数值模拟研究[J]. 中国矿业大学学报, 2015, 44(3)：423- 429．

[11] 张飞, 王宏沛, 徐光黎, 等. 地下厂房洞室群岩体参数的增量位移反分析[J]. 水电能源科学, 2012, 30(12)： 94- 97, 214.

[12] 向天兵. 大型地下厂房洞室群施工期动态反馈优化设计方法研究[D]. 武汉： 中国科学院研究生院(武汉岩土力学研所), 2010．

[13] 黄书岭, 王继敏, 丁秀丽, 等. 基于层状岩体卸荷演化的锦屏I级地下厂房洞室群稳定性与调控[J]. 岩石力学与工程学报, 2011, 30(11)： 2203- 2216．

[14] 王润英, 李天翔, 曾凤华. 基于小波神经网络的混凝土热力学参数反演[J]. 水电能源科学, 2014, 32(12)： 107- 109．