基于巴西劈裂试验的混凝土细观本构模型参数估计方法
2018-06-22志云大连理工大学工业装备结构分析国家重点实验室辽宁大连604大连海洋大学海洋与土木工程学院辽宁大连603
, ,志云(. 大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 604;. 大连海洋大学 海洋与土木工程学院,辽宁 大连 603)
混凝土材料通常指由水泥为胶凝材料,砂、石作骨料,与水(可含外加剂和掺合料)按一定比例配合,经搅拌而得的水泥混凝土。在土木工程结构中,混凝土材料得到了大量的应用,其抗拉能力比抗压能力弱很多,然而在一些极端情况下,混凝土材料可能会承受较大的拉力从而引起结构破坏。巴西劈裂试验是测定岩石类材料抗拉强度的方法之一,也是国际岩石力学学会(international society for rock mechanics, ISRM)[1]和美国材料试验学会(american society for testing and materials, ASTM)[2]推荐的测量岩石材料抗压强度的试验方法。由于混凝土与岩石力学性能相近,有许多学者利用巴西劈裂试验测量混凝土的抗拉强度[3-6]。Cundall和Strack于20世纪70年代基于牛顿第二定律提出了离散单元法(discrete element method, DEM)的概念。相比基于连续介质力学的有限单元法,离散单元法对于模拟混凝土的开裂、裂纹扩展等大变形有一定的优势。Qin等[7]基于质点单元法,建立了不同应变率下混凝土骨料、砂浆和界面三相细观动力学模型,研究表明应变率越高,网状裂纹产生的越多,试样的力链产生更多分支,意味着在更高的应变率下需要更多的能量达到失效。Ghazvinian等[8]用PFC2D模拟了含非贯通节理的岩石材料的剪切特性,离散元模拟表明宏观剪切带是张拉破坏产生的微裂纹扩展引起的。Mechtcherine等[9]介绍了用离散单元法模拟混凝土流动领域的发展,给出了参数估计的各种例子并与试验结果进行了比较,显示出离散单元法的潜力。Pan等[10]用PFC2D建立了混凝土三相细观模型,进行了单轴压缩试验来研究碱集料反应对混凝土力学性能的影响,结果表明这一模型可以有效预测碱集料反应引起的混凝土内部微裂纹的扩展。Kazerani等[11]提出了一个检验岩石强度和失效的离散元模型,两个相邻颗粒的边界被视为柔性接触,其本构关系控制材料的断裂性能,基于单轴/三轴压缩和巴西劈裂试验提出一套细观参数并对比试验结果验证了方法的有效性。
离散元单元法与有限单元法相比,最大的区别是不可能通过直接赋值的形式实现对材料的宏观基本物理力学参数的确定,仅取决于颗粒的细观本构模型参数。离散元只可以直接赋值颗粒的几何特征(颗粒大小和分布)和颗粒间接触的细观力学参数(细观本构模型和刚度、摩擦系数等接触力学特征),这些细观参数的改变意味着材料的宏观力学特性的显著改变。而如何定量确定混凝土材料离散元模型的细观参数是制约该方法进一步深入研究和工程实际应用的瓶颈问题之一。混凝土骨料粒径经常是毫米量级的,在该尺度上直接测量其细观参数是极其困难的,通用的方法是试错法(hit-and-miss),即不断调整细观参数反复计算直到获得一组与宏观响应吻合较好的细观参数。然而这样的方法往往存在着参数调整缺乏方向性和目的性等问题,造成效率低下。本研究提出一种基于巴西劈裂试验的混凝土细观本构模型参数估计方法,即先建立试验件离散元模型,给出一组细观参数估计值,接下来分别改变每个细观参数的取值,利用线性回归确定每个细观参数对宏观变量的影响系数,进而确定试样的最大承载力及其对应的最大位移与细观参数间的关系,求解一个约束优化问题,即可求得一组计算结果与实际试验曲线较为接近的细观参数。该方法的主要优势是只使用一组试验数据并进行少量PFC2D计算,即可得到一组满足工程需求的细观参数。
1 PFC2D中的细观本构模型
在某一时刻,PFC2D程序根据牛顿第二定律确定颗粒的加速度,并通过差分法得到颗粒在这一时刻的位移。而将力和位移联系起来使计算能够循环进行下去的关键条件,就是细观本构模型。PFC2D中常用的细观本构模型主要有三种:一是接触刚度模型,主要描述颗粒相互接触运动时法向和切向的挤压力;二是滑移模型,主要描述颗粒间存在相互滑动趋势时的力学行为;三是粘结模型,主要描述黏性颗粒的抗拉和抗剪能力。接触刚度模型中,常用的是线性接触模型,利用接触的法向刚度Kn和切向刚度Ks两个参数将颗粒间的法向、切向力和重叠量联系起来。
(1)
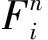
(2)
其中:ξ={n,s},n,s分别表示法向和切向。滑移模型可以表示为
(3)


对于PFC2D中的接触刚度模型和平行粘结模型,都可以视为两颗粒及连接其圆心的弹性梁组成的系统[12]。设弹性梁的弹性模量为Ec(接触弹性模量),由弹性力学解可得
kn=2Ect。
(4)
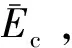
对于混凝土材料而言,目前并没有明确的标准规定采用哪些细观本构模型来进行计算,表1列出的是不同学者研究混凝土问题时所采用的细观模型参数。

表1 某些材料的细观本构模型参数取值Tab.1 Microparameters of micro-constitutive model for some materials
注:n_bond和s_bond分别为接触粘结模型抗拉和抗剪强度
2 混凝土细观本构模型参数估计方法
巴西劈裂试验主要用来测试岩石材料的抗拉强度,通常是根据弹性力学解由试样的最大承载力求得其抗拉强度。试样在破坏前处于弹性变形阶段,其荷载-位移曲线呈一近似直线。本研究主要目的是寻找一组合适的细观参数使仿真得到的试样宏观力学响应与试验结果吻合,因此重点关注试样的最大承载力Fmax和其对应的最大位移dmax。宏观响应与细观参数之间存在着一定的函数关系,通常情况下,这些函数关系难以显式表达出来,因此也就无法直接利用宏观响应确定细观参数取值。为简化这些函数关系,假定宏观响应是细观参数的线性叠加,且不同细观参数之间不存在耦合,即:
(5)
(6)
其中:Xi表示细观参数,ai和bi表示线性回归系数,a0和b0为待定常数。为进行细观参数的估计,先给定一组细观参数初始值,对每一个细观参数,在其他参数取值不变的情况下,单独改变该参数的取值。分别取X={…,Xi,…},X={…,Xi±ΔXi,…}和X={…,Xi±2ΔXi,…}5组细观参数进行PFC2D模拟,得到5个与Xi不同取值对应的Fmax的值。以Xi为自变量对Fmax进行线性回归,得到回归直线方程和相关系数R2,回归直线的斜率即为Xi对Fmax的线性回归系数ai。同理求出细观参数对dmax的线性回归系数bi。此外,通常认为相关系数R2≥0.7时,两变量具有相关性。基于这一考虑,当某一细观参数对Fmax或dmax的相关系数R2<0.7时,认为其对应的线性回归系数ai或bi为0,即这一细观参数的取值变化对最大承载力Fmax或其对应的最大位移dmax没有影响。将ai和bi与对应的细观参数初始值相乘,所得结果与模拟得到的宏观响应之差即为待定常数a0和b0。
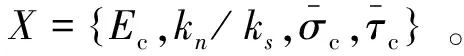
(7)
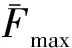
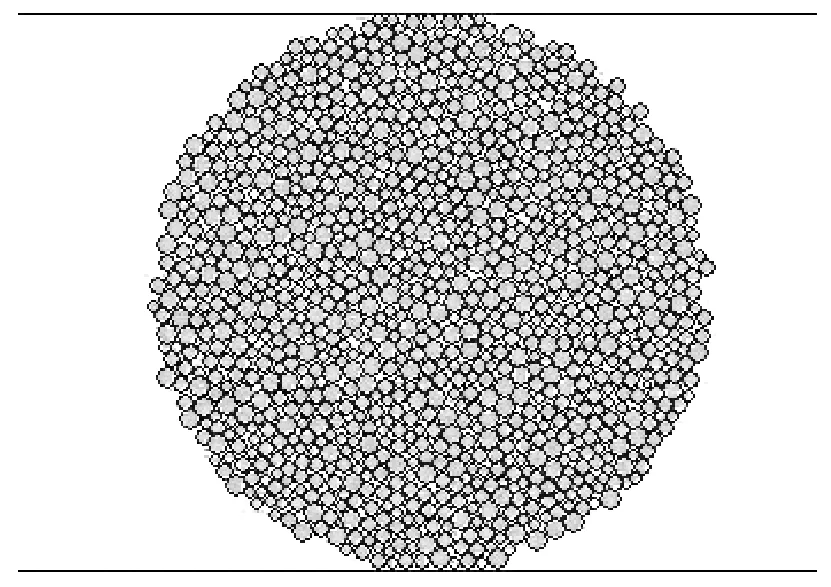
图1 巴西劈裂试验PFC2D模型Fig.1 PFC2D model of Brazilian test
3 算例分析
翟越等[18]对C35商品混凝土试件了进行巴西劈裂试验,试样厚度50 mm,直径100 mm。在PFC2D中建立这一试样的离散元模型(如图1),试样共由1 078个颗粒组成,颗粒半径在1.0~2.0 mm内均匀分布,颗粒厚度为50 mm,利用刚性墙对试样施加荷载。根据文献[14-15],表2给出了细观参数的初始值。
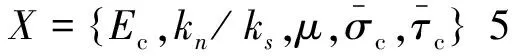

表2 C35混凝土细观参数的初始值Tab.2 Initial estimation of C35 concrete microparameters
由图2可以看出,随着接触弹性模量Ec的增大,试样的最大承载力呈减小趋势,最大承载力对应的最大位移也逐渐减小。由图3可以看出kn/ks取值的改变主要影响试样最大承载力对应的最大位移,最大位移随kn/ks的增大而增大。kn/ks取值的改变对最大承载力的影响并无明显规律。
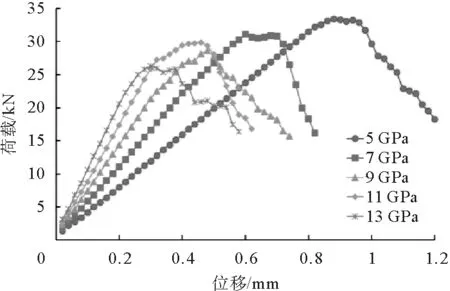
图2 Ec对荷载-位移曲线的影响Fig.2 Influence of Ec on load-displacement curves

图3 kn/ks对荷载-位移曲线的影响Fig.3 Influence of kn/kson load-displacement curves
由图4可以看出,随着摩擦系数μ的增大,试样的最大承载力也逐渐增大,最大承载力对应的最大位移呈减小趋势。摩擦系数的增大,限制了颗粒间滑移的发生,从而提高了承载力,减小了最大位移。
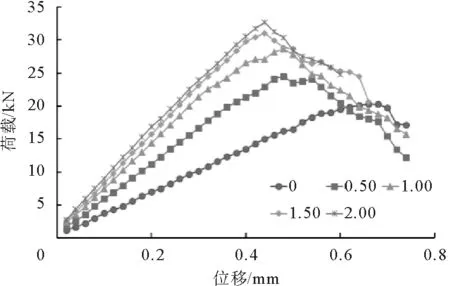
图4 μ对荷载-位移曲线的影响Fig.4 Influence of μ on load-displacement curves

图对荷载-位移曲线的影响Fig.5 Influence of on load-displacement curves
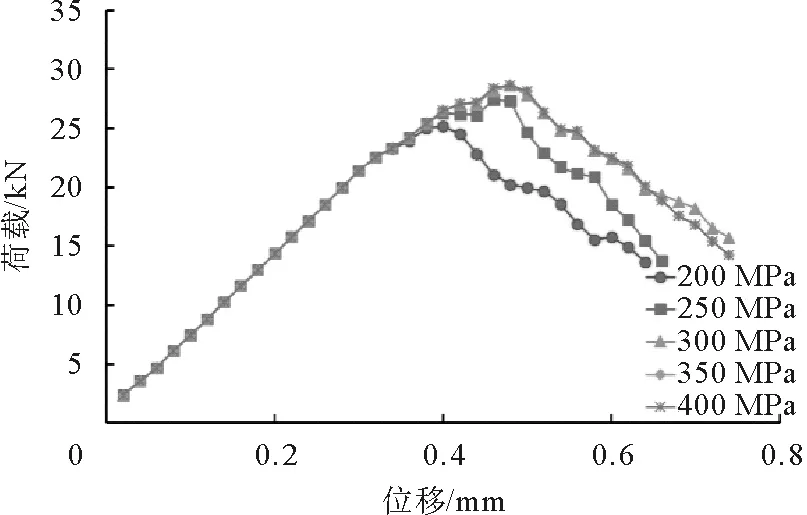
图对荷载-位移曲线的影响Fig.6 Influence load-displacement curves
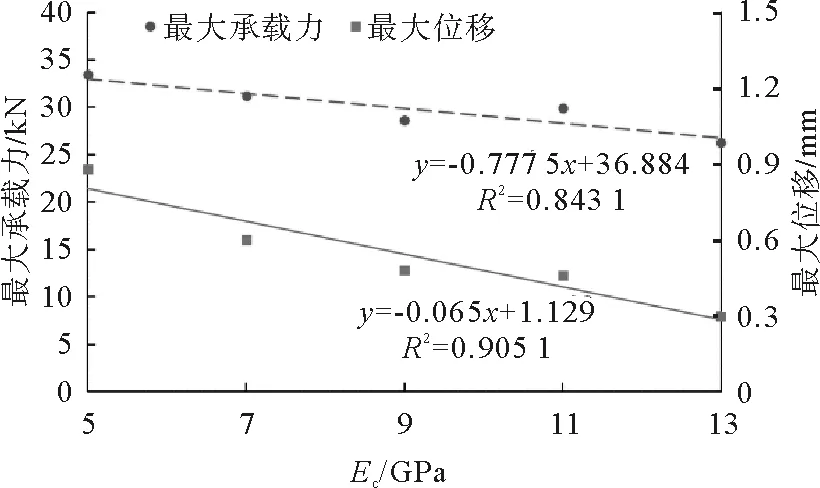
图7 宏观响应随Ec的变化Fig.7 Variation of macroscopic response versus Ec
根据图2~6所获得的信息,绘制不同细观参数对应的最大承载力和最大位移散点图(图7~11)。以各个细观参数为自变量对最大承载力和最大位移进行线性回归,得到回归直线方程和相关系数R2也显示于图7~11中。
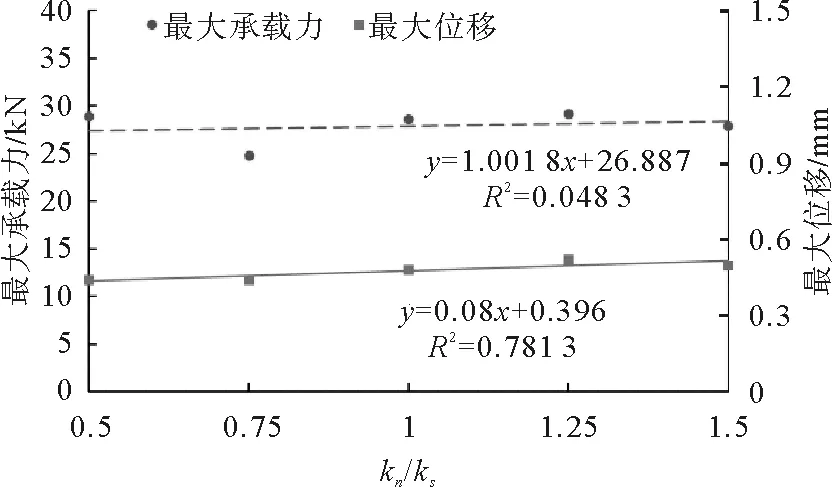
图8 宏观响应随kn/ks的变化Fig.8 Variation of macroscopic response versuskn/ks
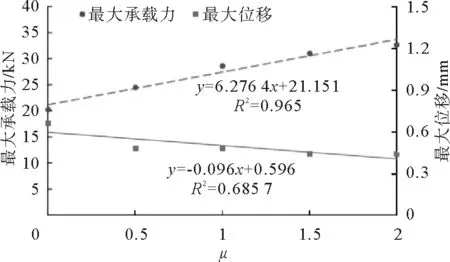
图9 宏观响应随μ的变化Fig.9 Variation of macroscopic response versus μ
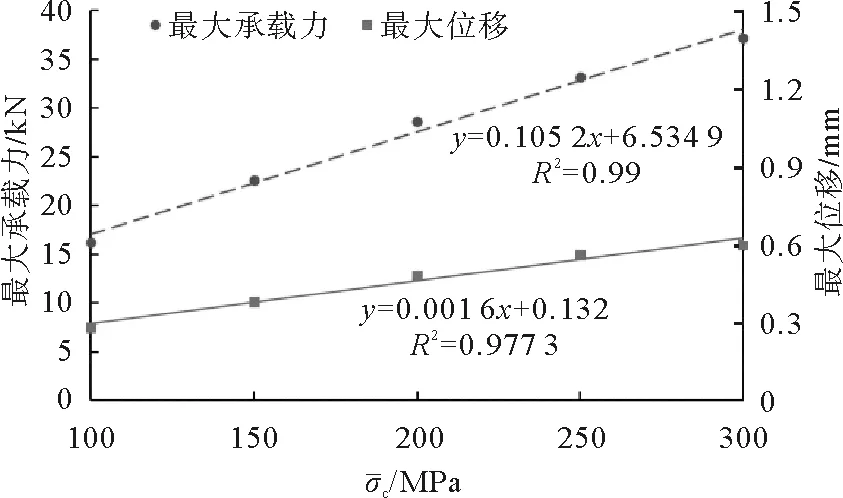
图10 宏观响应随的变化Fig.10 Variation of macroscopic response
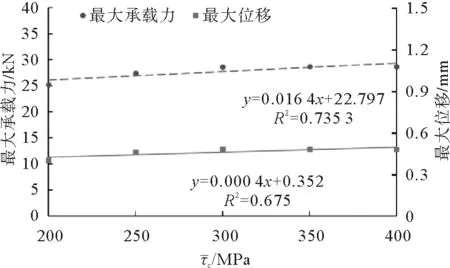
图11 宏观响应随的变化Fig.11 Variation of macroscopic response
表3中列出的是根据图7~11中的回归直线方程和相关系数确定的各细观参数的线性回归系数。将表2中C35混凝土细观参数初始估计值及表3中相应的线性回归系数分别代入式(5)~(6),即可计算得到待定常数ai和bi,从而得到宏观响应与细观参数近似的定量关系(式(8)~(9))。

表3 细观参数对宏观响应的线性回归系数Tab.3 Linear regression coefficients of microparameters to macroscopic response
(8)
(9)


表4 C35混凝土细观参数的估计值Tab.4 Estimated values of C35 concrete microparameters

图12 PFC2D模拟与试验荷载-位移曲线对比Fig.12 Comparison of load-displacement curves between PFC2D simulation and experiment
图12是使用细观参数初始值和估计值进行PFC2D模拟所得荷载-位移曲线与试验结果的对比,通过模拟得到的两条曲线与试验曲线的相关系数分别为R2=0.767,R2=0.978,可以看出,使用估计值模拟得到的结果更加接近试验曲线。但这一曲线在接近峰值承载力时出现下降然后略有上升的现象,这是由于与压板接触处的颗粒因应力集中而提前破坏后进一步压实所产生的。试样断裂面及PFC2D模拟裂纹分布情况分别如图13(a)、(b)所示,图13(b)中深黑色表示颗粒间胶结体拉伸破坏,灰色表示胶结体剪切破坏。

图13 试验[18]与PFC2D模拟裂纹分布情况对比Fig.13 Comparison of crack distributions between test observation and PFC2D simulation
表5给出的是使用细观参数初始值和估计值进行模拟与试验曲线在不同位移处所得相对误差的对比。可以看出,使用经过优化之后的细观参数估计值计算得到的结果误差明显小于使用初始值得到的结果。

表5 使用不同参数在各个位移处的误差对比Tab.5 Comparison of errors at each displacement using different parameters
由图12~13和表5可以看出,使用表4中的细观参数估计值,可以有效地模拟出混凝土试件在巴西劈裂试验中的力学行为和破坏过程,模拟曲线与试验曲线在整体变化趋势上一致,最大承载力及其对应的最大位移与试验结果比较接近。
4 结论
1) 离散元单元法的原理决定了只可以对颗粒的细观参数进行赋值,如何使细观参数计算结果与宏观试验结果吻合对PFC方法的应用是极其重要的。基于混凝土试样的巴西劈裂试验,提出了使用一组试验数据并进行少量PFC2D计算以得到一组满足工程需求的细观参数的方法,避免了试错法进行参数调整的盲目性,节约了参数估计的时间。
2) PFC2D混凝土试样的最大承载力与Ec和μ相关,最大承载力随着Ec的增大而减小,随着μ的增大而增大;试验最大承载力所对应的最大位移与Ec和kn/ks相关,最大位移随着Ec的增大而减小,随着kn/ks的增大而增大;试验荷载-位移曲线的斜率也与Ec和μ相关,斜率随着二者的增大而增大。

4) 利用本研究提出的细观参数估计方法,得到了C35混凝土试件离散元细观参数,PFC2D模拟结果表明,模拟曲线与试验曲线吻合较好,两者相关系数R2为0.978,验证了该方法的有效性。
参考文献:
[1]BIENIAWSKI Z T,HAWKES I.Suggested methods for determining tensile strength of rock materials[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1978,15:99-103.
[2]ASTM C496-85.Standard test method for splitting tensile strength of cylindrical concrete specimens[S].Annual Book of ASTM Standards 4,1986:337-342.
[3]CHEN X D,GE L M,ZHOU J K,et al.Dynamic Brazilian test of concrete using split Hopkinson pressure bar[J].Materials and Structures,2017,50(1):1-15.
[4]CARMONA S,AGUADO A.New model for the indirect determination of the tensile stress-strain curve of concrete by means of the Brazilian test[J].Materials and Structures,2012,45(10):1473-1485.
[5]OHTSU M,KAWASAKI Y.AE-SiGMA analysis in Brazilian test and accelerated corrosion test of concrete[J].Journal of Acoustic Emission,2010,28:204-214.
[6]ABRISHAMBAF A,BARROS J,CUNHA V.Relation between fibre distribution and post-cracking behaviour in steel fibre reinforced self-compacting concrete panels[J].Cement & Concrete Research,2013,51(9):57-66.
[7]QIN C,ZHANG C H.Numerical study of dynamic behavior of concrete by meso-scale particle element modeling[J].International Journal of Impact Engineering,2011,38(12):1011-1021.
[8]GHAZVINIAN A,SARFARAZI V,SCHUBERT W,et al.A study of the failure mechanism of planar non-persistent open joints using PFC2D[J].Rock Mechanics and Rock Engineering,2012,45(5):677-693.
[9]MECHTCHERINE V,GRAM A,KRENZER K,et al.Simulation of fresh concrete flow using discrete element method (DEM):Theory and applications[J].Materials and Structures,2014,47(4):615-630.
[10]PAN J W,FENG Y T,JIN F,et al.Meso-scale particle modeling of concrete deterioration caused by alkali-aggregate reaction[J].International Journal for Numerical & Analytical Methods in Geomechanics,2013,37(16):2690-2705.
[11]KAZERANI T,YANG Z Y,ZHAO J.A discrete element model for predicting shear strength and degradation of rock joint by using compressive and tensile test data[J].Rock Mechanics and Rock Engineering,2012,45(5):695-709.
[12]ITASCA Consulting Group Incorporated.Particle flow in two-dimensions version 3.1 user manual[M].Minneapolis:ITASCA Consulting Group Incorporated,2005.
[13]张宁.碾压混凝土碾压特性的三维离散元数值模拟[D].杭州:浙江大学,2015.
[14]张正珺,刘军,胡文,等.混凝土材料破坏过程的二维离散元模拟[J].水力发电学报,2010,29(5):22-27.
ZHANG Zhengjun,LIU Jun,HU Wen,et al.Two-dimensional simulation of concrete material fracturing by discrete element method[J].Journal of Hydroelectric Engineering,2010,29(5):22-27.
[15]唐阳,陶承品,徐霖玉,等.基于PFC2D的植生混凝土虚拟试验研究[J].水利科技与经济,2012,20(12):10-13.
TANG Yang,TAO Chengpin,XU Linyu,et al.Research on virtual tests of green-growing concrete based on PFC2D[J].Water Conservancy Science and Technology and Economy,2012,20(12):10-13.
[16]丛宇.卸荷条件下演示破坏宏细观机理与地下工程设计计算方法研究[D].青岛:青岛理工大学,2014.
[17]李守巨,李德,于申.基于宏观实验数据的堆石料细观本构模型参数反演[J].山东科技大学学报(自然科学版),2015,34(5):20-26.
LI Shouju,LI De,YU Shen.Meso-parameter inversion of constitutive model for rockfill materials based on marco experimental data[J].Journal of Shandong University of Science and Technology (Natural Science),2015,34(5):20-26.
[18]翟越,赵均海,艾晓芹,等.基于统一强度理论的巴西圆盘劈裂强度分析[J].建筑科学与工程学报,2015,32(3):46-51.
ZHAI Yue,ZHAO Junhai,AI Xiaoqin,et al.Analysis on splitting of Brazilian disc based on unified strength theory[J].Journal of Architecture and Civil Engineering,2015,32(3):46-51.
[19]刘运思,傅鹤林,饶军应,等.不同层理方位影响下板岩各向异性巴西圆盘劈裂试验研究[J].岩石力学与工程学报,2012,31(4):785-791.
LIU Yunsi,FU Helin,RAO Junying,et al.Research on Brazilian disc splitting tests for anisotropy of slate under influence of different bedding orientations[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(4):785-791.
