基于障碍物斥力场的汽车主动避撞系统＊

方俊

（北京京北职业技术学院，北京 101400）

1 前言

随着汽车保有量的快速增长与相对缓慢的道路建设之间的矛盾日益突出，交通事故成为人类非正常死亡的第一杀手[1]，研究汽车主动避撞系统对保护人身财产安全具有重要意义。

汽车主动避撞过程是指当探测到障碍物的存在时能够规划出一条避撞路径且能够跟随此路径[2-3]。目前常用的路径规划方法包括人工势场法、遗传算法、快速搜索随机树、神经网络算法[4-6]等，但这些方法不仅存在算法自身缺陷，而且求解效率低、耗时长。

为了避免路径规划中的迭代过程，提高规划实时性，本文建立了道路算盘模型和驾驶员预瞄跟随模型。经仿真验证，算盘模型规划出的路径平滑、安全、可跟踪；驾驶员预瞄跟随模型的路径跟随精度高，实现了汽车主动避撞。

2 主动避撞系统设计

设计的汽车主动避撞系统分为4个模块，分别为环境感知模块、信息处理模块、局部路径规划模块和路径跟踪模块，如图1所示。

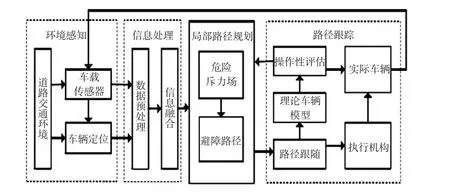
图1 汽车主动避撞系统

环境感知模块用于测量车道线、车道数、路长、路宽、障碍物大小、位置、速度、自车当前位置、车速、制动踏板信息、转向盘转向角信息；信息处理模块进行数据预处理和信息融合；局部路径规划模块根据当前汽车的测量信息规划出一条能够避开障碍物且符合汽车性能指标的最优路径；路径跟踪模块对规划出的避撞路径进行跟随。

3 局部路径规划

3.1 道路算盘模型

如图2所示，算盘与典型的平直双车道道路非常相似，借鉴算盘的构造可建立避撞道路的算盘模型。

图2 道路与算盘类比

设置平直或者近似平直的双车道宽度为B，在车辆的探测距离L内等间距地插入n-1根细杆，在每根细杆中穿入一个算珠，算珠在外力作用下只能沿着细杆上下运动。在算珠间使用等刚度的弹簧进行连接，第一根弹簧的起点、第一个算珠的位置、汽车的质心位置三者重合，最后一根弹簧末端固定在目标点上。在汽车行驶过程中，算珠不仅受到弹簧的拉力作用，还受到道路边界和障碍物的斥力，算珠在这些力的综合作用下达到稳定状态，稳定后的位置即为汽车的无碰撞路径。道路算盘模型如图3所示。

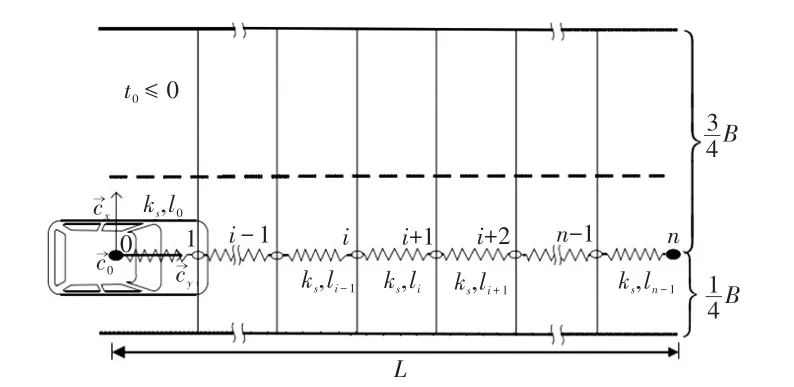
图3 道路算盘模型示意

为便于描述，分别建立了汽车坐标系和道路坐标系，如图4所示。汽车坐标系C*(c0,cx,cy)以汽车质心为坐标原点，汽车的前进方向为X轴，与前进方向垂直为Y轴；道路坐标系E*(e0,ex,ey)以第1个算珠所在位置为原点，道路横向为X轴，纵向为Y轴。

图4 斥力平衡状态

3.2 算盘模型的数学描述

建立边界线斥力模型、障碍物斥力模型和弹簧力模型，进而得到算珠的受力平衡模型。

3.2.1 边界线斥力建模

将道路边界线视为障碍物，道路的左右边界线对内部的算珠具有斥力作用，且越靠近边界斥力越大。以图5所示情况为例，第i根细杆与道路边界的交点对此细杆上的算珠有排斥作用，参考万有引力公式，道路边界线的斥力计算方法为：

式中，Fi,l、Fi,r为道路两个边界的斥力；kl、kr为两个边界的斥力系数为Y轴的单位矢量为3个位置矢量。

图5 道路边界斥力场

为使汽车在无障碍物的情况下可沿着道路中心行驶，对边界的斥力系数进行了界定，即，若使汽车沿右侧道路中心行驶，要求；若要使汽车沿左侧道路中心行驶，则要求

3.2.2 障碍物斥力建模

前文将自车的运动看作一个质心运动，而实际情况下必须考虑汽车尺寸才不会发生碰撞，因此将障碍物车辆用一个直径为两倍车宽的安全圆包围，在安全圆边界上建立斥力场，对穿过安全圆的细杆上的算珠产生斥力作用，且算珠越接近斥力场则排斥力越大，但对于未穿过障碍物的算珠斥力为0，障碍物斥力场如图6所示。同样参考万有引力公式，障碍物对算珠的斥力为：

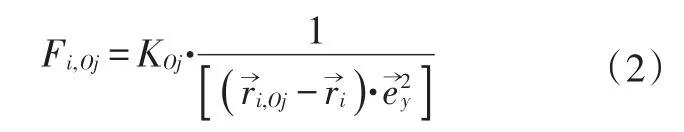
式中，Fi,Oj为障碍物对算珠的斥力；KOj为斥力系数；为位置矢量。

3.2.3 弹簧弹力建模

当自车前方出现障碍物时，算珠在边界斥力、障碍物斥力、弹簧弹力的综合作用下达到稳定状态，此时将算珠的轨迹进行平滑性拟合即可得到最优轨迹。算珠i受到的弹力由与之相连的两根弹簧施加，如图7所示。

图6 障碍物斥力场示意

图7 弹簧弹力

第i-1根弹簧对算珠的拉力为：

式中为弹簧对算珠的拉力；ks为弹簧系数；||为向量的模；l0为弹簧的原始长度。

第i+1根弹簧对算珠的拉力参考式（3）给出。

3.2.4 受力平衡模型

由以上分析可知，每个算珠受到边界斥力、障碍物斥力、弹簧弹力等3种力的作用。当自车前方有m个障碍物时，算珠受到的力平衡模型为：

式（4）是一个非线性方程组，可以使用牛顿迭代法[7]求解。因算珠之间的距离已知，则算珠的横坐标可确定，因此对式（4）的求解实质是求道路坐标系纵坐标，使用平滑曲线将纵坐标连接就得到了避障轨迹。

4 路径跟随系统

4.1 驾驶员预瞄跟随模型建立

驾驶员预瞄跟随模型根据控制对象的不同可以分为方向控制、速度控制、方向-速度联合控制三类[8]，由于对路径的跟随只与方向有关，因此本文使用方向控制的驾驶员预瞄跟随模型。驾驶员预瞄跟随模型描述为：驾驶员以前方一定距离的某点为目标点（也叫预瞄点），根据汽车当前的行驶状态预测汽车到达该目标点的实际轨迹，根据预测轨迹与目标轨迹的偏差调整转向盘转角，使汽车能够跟随预先规划的路径，直至到达预瞄点[9,10]。

驾驶员预瞄跟随模型如图8所示。图8中，f为目标路径；fe为驾驶员根据汽车当前状态预测的汽车位置信息；ε为位置误差；δ为转向盘转角；y为汽车实际位置信息，yp为汽车位置反馈信息，F（s）为跟随器传递函数。求解轨迹跟随模型的本质是给出模型中的δ。

图8 驾驶员预瞄跟随模型

4.2 最优转向盘转角求解

在不考虑汽车动态响应的情况下，车辆的转动服从Acklman几何关系，即

式中，R为汽车的转弯半径；L为汽车的轴距。

式中，y（t）为汽车侧向位移为汽车侧向速度为侧向加速度。

目标路径函数记为f(t)，汽车在时刻t的状态记为y(t)。假设驾驶员的前视距离为d，则相应的前视时间为T=d/v（v为车速），汽车在时刻t+T的侧向位移为：

根据误差最小原则，驾驶员希望实际路径与目标路径误差最小，则由式（7）得：

结合式（6），最优转向盘转动角度为：

5 仿真验证

5.1 试验1

试验1情景如图9所示，汽车以90 km/h的速度在双同向车道的平直公路上行驶，路宽为7 m，路长为250 m，汽车右侧行驶，在自车车道前方40 m处存在一个静态障碍物，同时在左侧车道距自车150 m处存在另一静态障碍物，若自车继续按当前状态行驶，则1.6 s后汽车与自车车道障碍物相撞。

图9 试验1情景

针对试验1情景，利用牛顿迭代函数求解道路的算盘模型得到避障路径，利用驾驶员预瞄跟随模型对路径进行跟随，结果如图10所示。

图10 试验1情景下汽车路径规划及路径跟踪结果

由图10a可看出，使用算盘模型规划出的路径能够安全避开障碍物，且路径平滑；由图10b可看出，驾驶员预瞄跟随模型能够很好地跟踪规划路径，两条路径吻合程度较高；由图10c可看出，为跟踪避撞路径，在0 s时汽车转弯角度较大，即转向盘转角大，至1.5 s时汽车位于第1个障碍物左侧，然后汽车转向盘回转，使汽车回到右侧车道。由于第2个障碍物不在右侧车道，所以在6 s左右时转向盘转角很小；由图10d和图10e可看出，汽车避撞过程中最大侧向加速度小于0.4g，最大横摆角速度小于12°/s，且整个过程中侧向加速度和横摆角速度没有突变的情况，说明路径合理，汽车能够安全稳定地跟踪规划路径。

5.2 试验2

试验2情景如图11所示，车速及路况与试验1相同。汽车右侧行驶，在自车车道前方40 m处某车以54 km/h的速度向前行驶，若自车继续按当前状态行驶，则4 s后发生追尾事故。

图11 试验2情景

针对试验2情景，利用牛顿迭代函数求解道路的算盘模型得到避障路径，利用驾驶员预瞄跟随模型对路径进行跟随，结果如图12所示。

由图12a可看出，使用算盘模型规划出的路径能够安全避开动态障碍物，且路径平滑；由图12b可看出，驾驶员预瞄跟随模型能够很好地跟踪规划路径，两条路径吻合程度很高；由图12c可看出，跟随路径过程中，转向盘转角曲率平滑，符合实际情况；由图12d和图12e可看出，汽车避撞过程中，最大侧向加速度为0.3g，最大横摆角速度为9°/s，且整个过程中侧向加速度和横摆角速度没有突变的情况，说明路径合理，汽车能够安全稳定地跟踪规划路径。

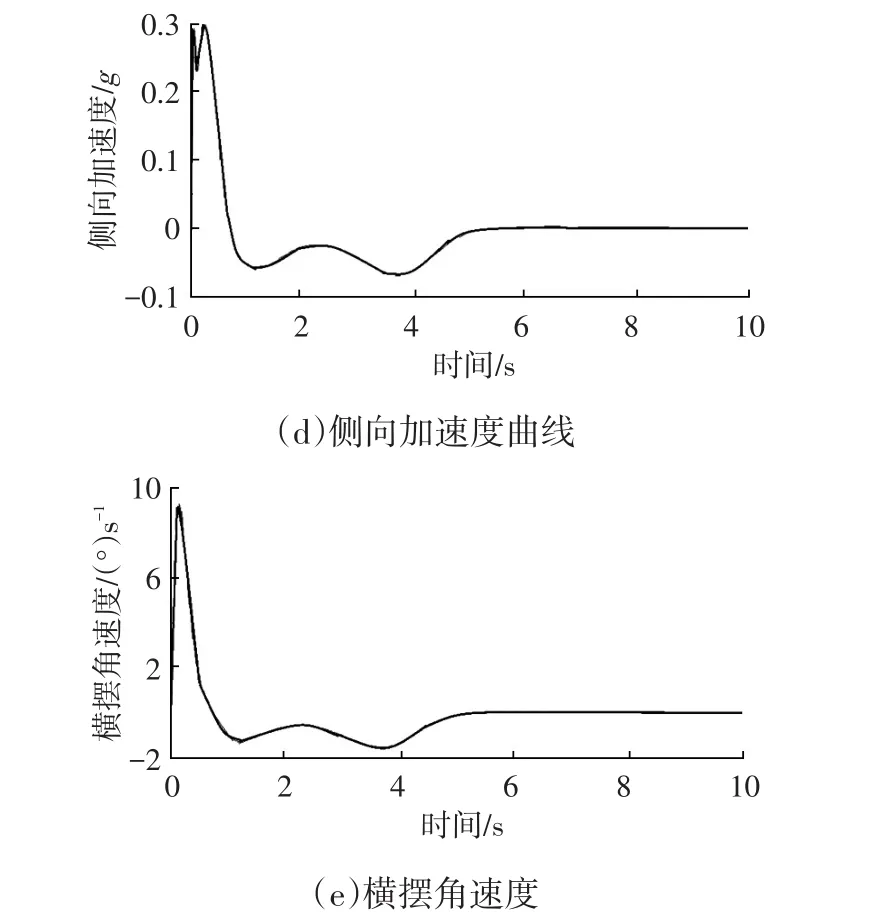
图12 试验2情景下汽车路径规划及路径跟踪结果

6 结束语

本文以车辆遇到障碍物时避撞为目的，设计了汽车主动避撞系统，建立了道路算盘模型和驾驶员预瞄跟随模型，利用算盘模型求解出了避撞路径，使用驾驶员预瞄跟随模型求解出了汽车转向盘最优转角。经仿真验证，算盘模型求解出的路径平滑、安全、可跟踪，驾驶员预瞄模型对规划路径具有很高的跟踪精度。

[1]孙轶轩.基于数据挖掘的道路交通事故分析研究[D].北京：北京交通大学,2014.

[2]孟琳,朱西产,孙晓宇,等.真实交通危险工况下驾驶员转向避撞相关因素分析[J].汽车技术,2016(6):59-62.

[3]李素华.采用dSPACE的电动汽车纵向主动避撞系统研究[J].机械设计与制造,2017(7):111-114.

[4]Zelek J S,Levine M D.Local-Global Concurrent Path Planning and Execution.IEEE Transaction on System,Man and Cybernetics,2000,30(6):865-870.

[5]Xiao J,Michalewicz Z,Zhang L X,Trojanowski K.Adaptive Evolutional Planner/navigation for Mobile Robots.IEEE Transactions on Evolutionary Computation,1997,1(1):18-28.

[6]章毅,郭泉,王建勇.大数据分析的神经网络方法[J].工程科学与技术,2017,49(1):9-18.

[7]Benner P,Ezzatti P.A Factored Variant of the Newton Iteration for the Solution of Algebraic Riccati Equations Via the Matrix Sign Function[J].Numerical Algorithms,2014,66(2):363-377.

[8]白艳,贾鑫.最优预瞄加速度驾驶员模型参数试验辨识方法研究[J].汽车工程,2015,37(7):788-793.

[9]陈名扬,朱西产,马志雄,等.不同驾驶员响应特性下的前碰撞预警安全收益分析[J].汽车技术,2016(11):51-55.

[10]黄满洪.考虑驾驶员预瞄特性的车辆稳定控制策略[D].南京：南京航空航天大学,2016.