液浮陀螺加速度计浮油模型的阻尼特性研究

2018-06-21刘珏高艺李军李亮牛文韬

长春理工大学学报（自然科学版） 2018年3期

刘珏，高艺，李军，李亮，牛文韬

（1.长春理工大学机电工程学院，长春 130022；2.北京航天控制仪器研究所，北京 100039）

液浮陀螺加速度计作为惯性导航和惯性制导系统的基本测量元件，用于测量运载体的线加速度，是重要的惯性器件。当前研制的新型摆式积分陀螺加速度计，同时采用气浮、液浮和磁悬浮三种支撑方式，具有高精度、高动态、大量程的特点［1，2］。

其中，液浮支撑功能依靠浮子周围的浮油发挥作用，其密度与浮子组件的平均密度相近，浮子的大部分重力被浮油的浮力平衡，残余的重浮力差由磁悬浮系统平衡，最终达到平衡状态。浮油通常采用高密度有机溶剂，具有较大的粘度和阻尼［3］。其中浮油的阻尼特性直接决定磁悬浮系统的出力大小、伺服回路的控制参数，进而影响仪表的动态精度。所以，对其阻尼的研究具有重要作用和意义。

由于浮油模型复杂且封闭，故浮油模型的阻尼研究一直未有很好的办法。本文通过合理简化得到浮油的阻尼仿真模型，然后进行浮子绕内环轴（即Y轴）旋转的阻尼测量试验，对比测量数据和仿真结果，验证了仿真分析方法的合理性。然后运用该方法研究浮子在平行运动状态下的浮油阻尼特性。

1 加速度计浮油仿真模型的建立

1.1 加速度计浮油的几何模型

在浮油模型阻尼特性的研究过程中，影响浮油阻尼的关键因素是浮油的形状和粘度。要想得到理想的浮油模型，需要对加速度计的结构模型进行合理简化。本文主要研究的是加速度计浮油模型的阻尼特性，故浮油模型遵循以下假设：

a.统计发现浮油的密度和粘度随温度线性变化；

b.加速度计的浮油区域无温度梯度，无湍流运动；

c.忽略零件的某些特征如倒角，但保留对阻尼影响大的过油孔及薄层油膜等。

参照上述假设，得到浮油的几何模型见图1。

图1 浮油的局部几何模型

1.2 加速度计浮油的计算模型

由于浮油充满整个内壳体，而位于内壳体中的零组件结构复杂，形状不规则，使浮油的阻尼研究难以通过理论计算得出。同时，浮油位于全封闭环境中，导致浮油阻尼特性无法通过试验进行测量。故选择流体仿真计算方法（Fluent软件）进行研究，其中流体仿真计算方法遵循以下原则［4-6］。

1）质量守恒方程

式中，ρ为密度；t为时间；ui为速度张量；xi为坐标张量。

2）动量守恒方程

在惯性坐标系下，i方向的动量守恒方程为：

式中，ρ为密度；t为时间；ui、uj为速度张量；xi、xj为坐标张量；ρgi为重力体积力；p是静压；Fi是重力体积力和其他体积力，Fi还可以包括其他模型源项或者自定义的源项。τij是应力张量，定义为：

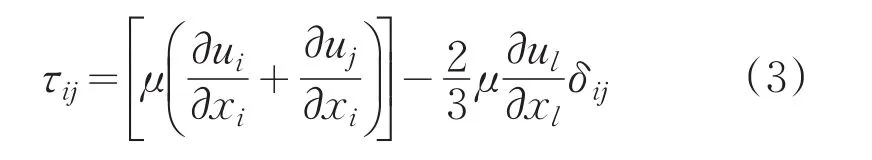
式中，μ为流体粘性系数；δij为克罗内克δ符号。

3）粘温特性

粘度是流体的重要参数，很大程度上影响了浮油的阻尼特性，粘温特性则描述了流体粘度随温度的变化规律［7，8］。本文从试验测得的粘温离散值数据出发，分析、验证和比较后发现，可将浮油的粘温特性关系看作线性变化。

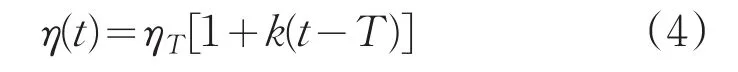
式中，ηT为温度为T时的浮油粘度，K为变化率。

2 仿真分析方法的合理性验证试验

为验证仿真分析方法用于浮油阻尼特性研究的合理性，进行了加速度计绕内环轴（即Y轴）转动的阻尼测量试验，对比测量结果与仿真结果，验证了研究方法的合理性，为分析平行运动状态下的阻尼特性奠定了理论基础。

2.1 阻尼系数测量试验

陀螺加速度计绕Y轴转动的阻尼系数测量试验，原理是利用加速度计浮子自身的摆性，使浮子在重力作用下绕Y轴在小角度内自由摆动（88°～92°）。通过仪表内部自身的角度传感器记录运动曲线，并拟合运动方程即可得到内环阻尼系数。

其中，内环阻尼摆的运动方程为：

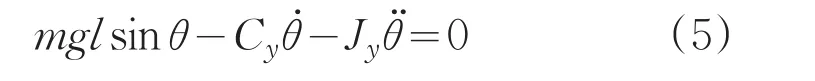
式中，m为浮子偏心配重的质量；l为浮子偏心配重的摆长；Cy为浮油阻尼系数；θ为浮子绕内环轴转过的角度；Jy为内环转动惯量。

由于试验操作是在小角度范围内，在自身重力作用下发生转动，加速度很小，可以忽略，故（5）式可简化为：

积分后得到阻尼系数的计算公式为：

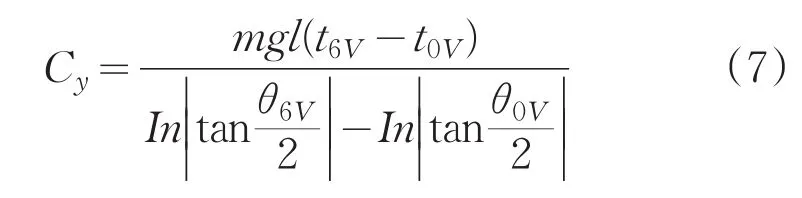
式中，t0V为传感器直流输出0V的时间；t6V为传感器直流输出6V的时间；θ0V、θ6V为对应时刻的角度。浮子组件旋转至限位结构时传感器输出约7V左右，为了提高测试精度，选取线性关系较强的运动过程进行计算，即0V～6V。试验中选取9只加速度计进行测试，各仪表的阻尼系数见图2，可认为绕内环轴的浮油阻尼系数为（8.6±0.6）×10-3N·m·s。

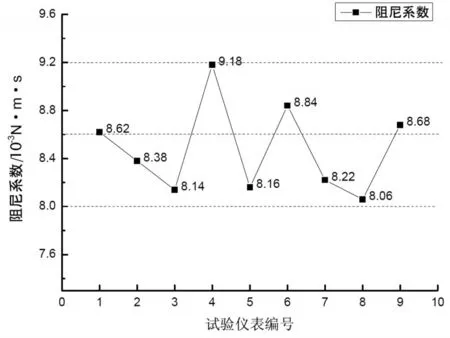
图2 阻尼系数统计

2.2 阻尼系数仿真试验

选用Fluent软件对简化后的模型进行仿真计算，对比阻尼系数测量试验。浮油模型中间位置处即环绕浮子的部分非常薄，仅为轴向尺寸的几百分之一，且整体模型复杂。故将其分为大端部分（大护线板组件端）、中段部分（浮子组件接触部分）、小端部分（小护线板组件端），分别进行网格划分，最终得到的网格模型如图3所示。

图3 网格模型

仿真过程中浮油参数见表1。仿真分析后得到浮油模型总的阻尼力矩为4.48×10-5N·m·s，计算后得到浮油的阻尼系数为9.16×10-3N·m·s，即通过Fluent软件计算得到的浮油绕内环轴转动的阻尼系数。

表1 浮油的物理参数

2.3 仿真分析方法合理性分析

在加速度计绕内环轴转动的阻尼测量试验中，运用加速度计结构的摆性特点，对浮油的阻尼系数进行试验测量，克服了仪表结构复杂、环境封闭的弊端，准确的得到了浮油绕内环轴转动的阻尼系数。随后，通过Fluent软件对浮油模型进行分析计算，对比测量试验和仿真试验的结果，基本接近，认为运用仿真分析方法对浮油阻尼特性进行研究是合理的，简化后的浮油仿真模型正确，可使用该模型分析浮油在平行运动状态下的阻尼特性。

3 平行运动状态下的阻尼特性研究

浮子组件在工作过程中，不仅存在由于外环摩擦力矩造成的浮子绕内环轴的旋转运动，还存在磁悬浮系统作用下沿坐标轴平行方向的运动。由于平行运动是在微米级范围内活动，无法通过试验进行测量。故采用Fluent软件研究平行运动状态下浮油的阻尼特性。

工作时浮子受磁拉力而处于悬浮状态，所以平行运动状态具有三个方向，分别为X轴（外环轴）、Y轴（内环轴）和Z轴（马达轴）三个方向，分别进行仿真计算。由于浮油模型是类回转体，具有中心对称性，经计算后发现沿X轴和Z轴两个方向的阻尼特性基本相同，故平动状态下的阻尼研究只需研究X轴和Y轴两个方向即可，部分计算结果见图4。

图4 各方向平动计算结果（v=0.01m/s）

3.1 粘度与浮油阻尼特性的关系

加速度计浮油模型的阻尼系数与浮油的粘度密切相关，而浮油的粘度随着温度的变化而改变，粘温特性遵循线性变化规律。通过实验测得变化率K为4.75%/℃，以某温度作为基准点，利用Fluent软件计算不同温度差下浮油的阻尼系数，结果见表3。

表3 Y方向不同温度条件下的阻尼系数

从计算数据可以看出，Y轴平动状态下，随着温度升高浮油的阻尼系数逐渐减小，且每2℃变化值为425N·s/m。X轴、Z轴平动状态下也类似，但每2℃变化值为112N·s/m。认为在浮油模型形状不变的情况下，阻尼系数变化主要受浮油粘度的影响。

3.2 运动速度与浮油阻尼特性的关系

由于浮油模型的形状在X和Y方向相差较大，需要研究不同方向平动状态下浮油阻尼特性的差异。对两方向进行了不同速度的仿真计算，结果见表4。

表4 不同速度下两方向的阻尼系数

从计算结果可以看出，沿Y轴方向的阻尼系数要比沿X轴方向的阻尼系数大的多，为4倍的关系，且阻尼系数基本不受平动速度的影响。其中，沿X轴方向运动的阻力主要来自中段受力，而沿Y轴方向运动的阻力主要来自小端受力。

3.3 浮油阻尼特性对仪表的影响

在陀螺加速度计设计过程中，浮油的阻尼特性直接影响浮子的工作状态。在平动方面，阻尼特性直接决定磁悬浮系统的出力情况，影响仪表的快速反应时间，合适的磁悬浮出力将有助于提高仪表的精度和稳定性。在转动方面，阻尼特性决定伺服回路的控制参数，从而保证浮子轴和外环轴的垂直度，并赋予整体系统以应有的静态和动态特性，保证系统稳定工作，使仪表具有所要求的精度［9］。所以，对浮油阻尼特性的研究直接影响浮子的工作状态，进而影响陀螺加速度计的精度和使用效果。