基于EKF修正算法的锂电池SOC估算

孙丽贝，屈薇薇

（西南科技大学信息工程学院，四川 绵阳 621010）

0 引言

荷电状态（SOC）的精确估算可以防止电池过充过放，能为续驶里程估计、延长电池寿命等提供有效的支持[1-2]。由于电动汽车在使用过程中的高度非线性使 SOC 估算成为当前研究的重点和难点，笔者针对 SOC 估算精度问题，分析其影响因素，建立准确的电池模型，采用 EKF 修正算法对其进行了仿真实验，并与安时积分法进行比较，验证了此方法的可行性和准确性。

1 算法原理与设计

1.1 常用 SOC 估算方法

由于受到充放电倍率、环境温度及电池内阻等诸多因素的影响，电池组的总容量在运行过程中表现出高度非线性和不确定性。目前，常用的 SOC估算方法有安时积分法、开路电压法、内阻推理法、神经网络法、卡尔曼滤波法等。其中，安时积分法是目前使用最为广泛的传统估算方法[3]。

1.1.1 安时积分法

安时积分法的基本思想是将电池不同放电电流等效为某特定电流的放电情况，是一种开环预测。该方法操作简单，能在短时间内准确估算 SOC，但存在 SOC 初始值难以准确获取的问题，并且随着时间的累积，电流测量不准，也会造成 SOC 估算误差越来越大，无法满足 SOC 实时在线估算的要求。

1.1.2 扩展卡尔曼滤波算法

为解决传统安时积分法存在的弊端，综合考虑充放电倍率、环境温度及电池内阻等因素的影响，采用扩展卡尔曼滤波算法对 SOC 进行估算。EKF是一种最小方差意义上的最优估计方法，基于反馈控制思想使系统形成闭环，适用于多维随机变量和电流波动较剧烈情况下的估计，在运算时可很快收敛到真值附近。另外，该算法对系统状态空间模型中的非线性函数做泰勒级数展开，仅保留线性项来获得线性模型，适应于具有高度非线性的电池系统。

1.2 SOC 动态观测方程的确定

采用卡尔曼滤波算法估算 SOC，考虑电动汽车运行环境的多变性与复杂性，需建立 SOC 动态观测方程[4]。

1.2.1 状态方程的建立

电池荷电状态（SOC）为电池剩余电量与额定容量的比值，对于动态电池系统，SOC 可表示为

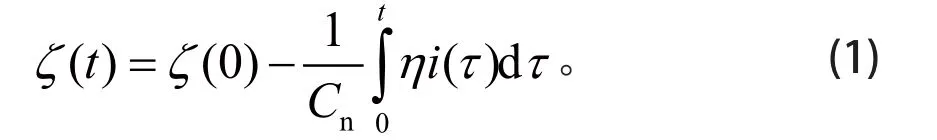
式中：ζ为电池荷电状态；η为库仑效率；i(τ)为电池在τ时刻的电流；Cn为电池额定容量。考虑到噪声影响，离散后状态方程为

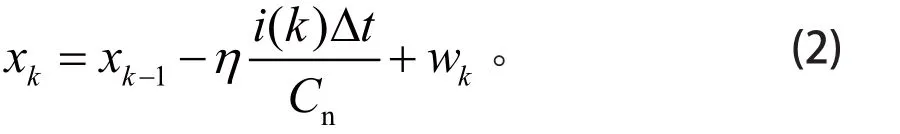
式中：xk、xk-1分别为k与k-1 时刻的系统状态向量,wk为系统噪声。

1.2.2 观测方程的建立

为增强动力电池开路电压（OCV）与 SOC 的关联性，提高卡尔曼滤波的收敛速度，采用简化的电化学模型[5]解析动力电池 OCV。在公式

中，ki（i=0, 1, ……, 5）为动力电池 OCV 与 SOC的拟合系数。为确定拟合系数，对一节处于满充状态的 45 Ah/4.2 V 动力锂电池，以标准放电速率放电至完全放电状态，记录放电过程中电池开路电压UOC与其对应的 SOC 值。采用最小二乘法拟合，可得如表 1 所示拟合系数，及如图 1 所示关系曲线。

表1 动力电池 OCV 与 SOC 拟合系数

图1 OCV 与 SOC 关系曲线

1.3 电池模型的建立

准确地选择电池模型不仅可以简化计算的复杂度，降低参数辨识的难度，而且可以准确地反应电池电动势与端电压之间的关系，提高估算的精度[6]。Thevenin 等效电路模型能很好地体现电池的特性，且它的阶数较低，便于研究。本文中所选取Thevenin 等效电路模型如图 2 所示。

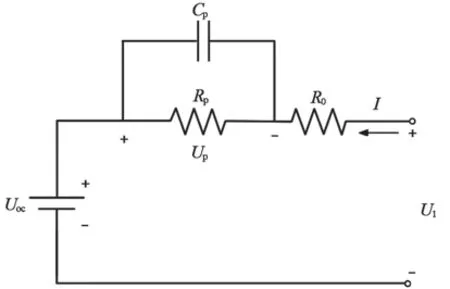
图2 Thevenin 等效电路模型

模型中各参数表征如下：UOC为开路电压；Ul为负载电压；I为电流；R0为电池的欧姆内阻；Up、Rp、Cp分别为极化电压、极化电阻和极化电容。

1.3.1 电池模型的离散化

分析等效电路模型，可得

由于动力电池模型参数在单位采样时间 Δt内可被看作定值，因此式（4）可化简为

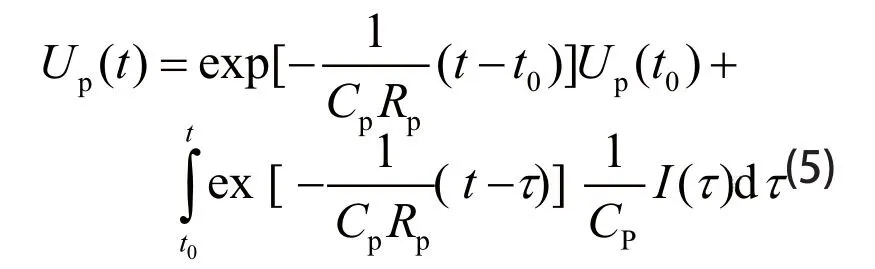
式（5）中：t0为初始时刻；t为当前时刻。进一步推导化简，可得动力电池模型中的极化电压为

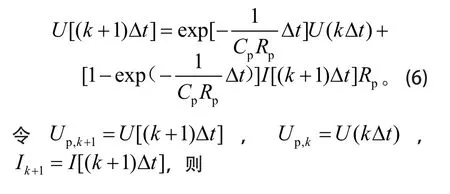
取ζ、Up为系统状态变量，I为系统输入，Ul为系统输出，结合式（4）和（7）可得电池模型描述方程

1.3.2 电池模型参数的辨识

准确辨识模型参数是建立电池模型的关键[7]。选取 45 Ah/4.2 V 单体动力锂电池为研究对象，对其进行混合脉冲功率特性（HPPC）测试，并按图3 所示操作流程进行模型参数辨识。各参数具体辨识方法如下：

（1）电池充放电停止瞬间，端电压会有一个微小的突变，反应了电池的内阻特性，利用此特性即可确定欧姆内阻R0。

（2）定义时间常数τ=CpRp，电池充放电静置时电流为零，可认为零输入响应。根据公式

采用最小二乘法拟合，可求出时间常数τ。

（3）HPPC 测试前，电池已静置足够长时间，因此可认为充放电过程中的响应是零状态的。根据公式

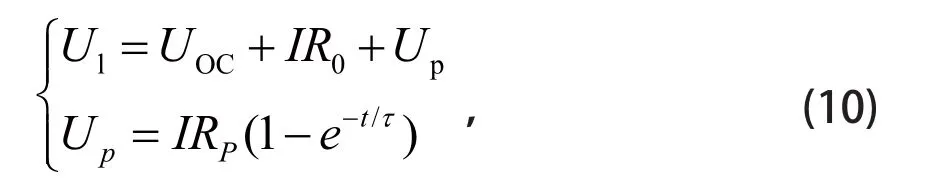
采用最小二乘法拟合，可求出极化电阻Rp，再根据τ=CpRp，即可求出极化电容Cp。各模型参数与SOC 的拟合关系如图 4 所示。

1.4 扩展卡尔曼滤波修正算法

EKF 算法是不断估算—修正的过程[8]，包括 2个信息更新过程，即时间更新和量测更新。时间更新为估算过程，用于推算当前的状态变量和误差协方差。量测更新为修正过程，利用系统的输出测量值对时间更新中得到的预测值进行修正，并不断循环往复，使预测值不断向真实值趋近。具体操作步骤如下：

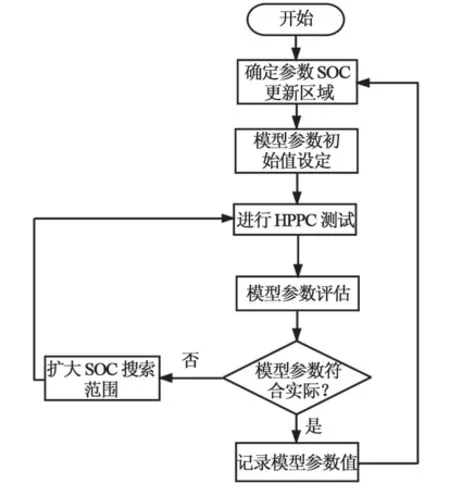
图3 模型参数辨识流程图

（1）确定系统状态空间模型中的矩阵参数Ak、Bk、Ck，非线性电池系统状态空间模型可以表示为

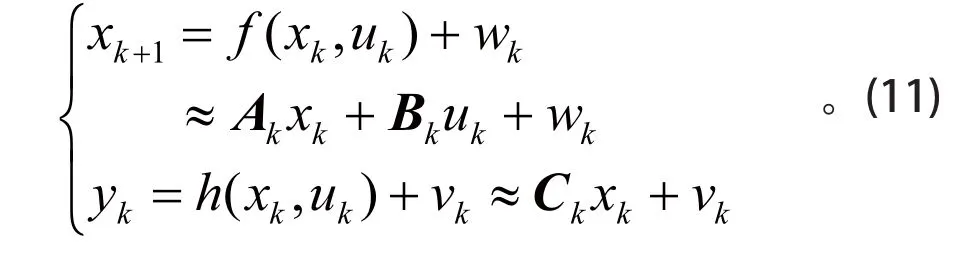
对非线性状态转移函数f(xk,uk)、非线性测量函数h(xk,uk) 进行线性化处理后，可得

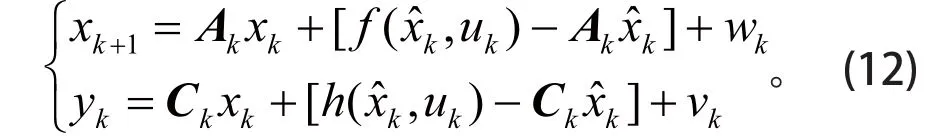
式（12）中：xk为k时刻的 SOC 值；为xk的估计值；uk为k时刻的电池充放电电流；yk为k时刻的电池电压；wk为系统噪声；vk为观测噪声。结合式（8）的电池模型描述方程，可得上式中各矩阵参数：

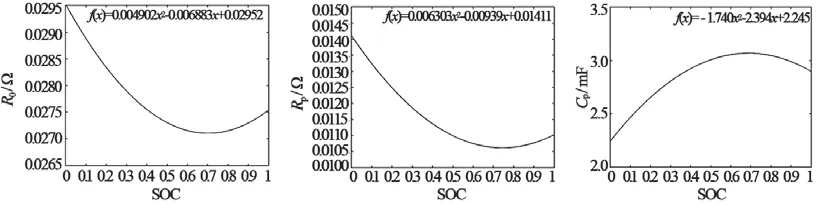
图4 R0、Rp、Cp 与 SOC 关系曲线

（2）确定滤波方程中电池初始荷电状态ζ(0)及误差协方差初始值P0。将锂电池静置足够长时间，根据图 1 即可确定荷电状态初始值ζ(0)。可由公式

和x0=ζ(0)确定误差协方差初始值P0。

（3）利用系统输入和上一时刻的最优估计值，确定当前时刻 SOC 预测值和输出电压预测值

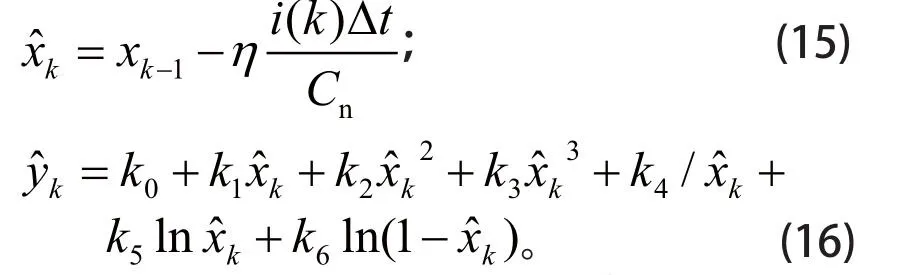
（4）确定误差协方差预测值进一步计算得到卡尔曼滤波增益矩阵

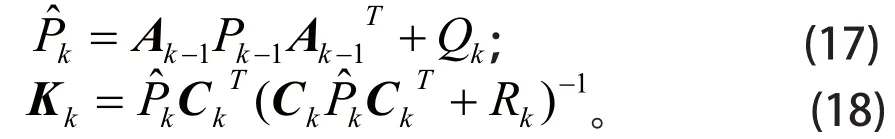
（5）利用系统输出电压对预测值进行修正，确定 SOC 的最优估计值xk和误差协方差的最优估计值Pk：

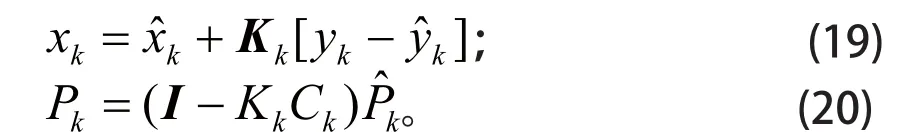
式（17）中，Qk为系统噪声误差协方差。式（20）中，Rk为量测噪声误差协方差；I为单位矩阵。

2 实验结果与分析

为了验证基于 Thevenin 等效电路模型的 EKF算法的可靠性和准确性，利用 MATLAB 进行了仿真实验[9]。图 5 中设置 SOC 初始值为 0.50，测量值为 0.90。由仿真结果可知，EKF 算法中 SOC 很快收敛到真实值附近，相比较安时积分法能迅速消除初始误差，对 SOC 初值有很强的修正能力。由图6 可知，随着时间累积，安时积分法产生的误差不断增大，而 EKF 估算预测值与实际输出值十分接近，最大估算误差在 2.0 % 以内，可有效解决安时积分法累计误差的问题。

图5 EKF 修正值、安时法计算值与实际输出值对比图

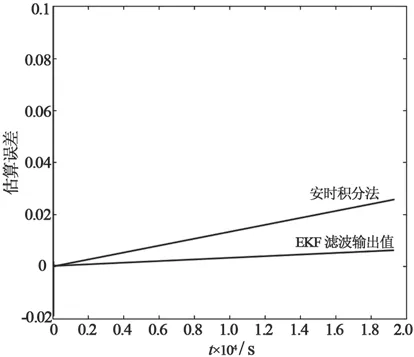
图6 EKF 与安时积分法估算误差曲线

3 结束语

本文中，笔者采取基于 Thevenin 等效电路模型的 EKF 算法实时监测动力蓄电池的 SOC 变化，根据实际情况合理辨识电池模型参数，利用MATLAB 进行仿真，并与安时积分法进行比较。仿真结果表明，EKF 修正算法能够实时准确地跟踪动力电池 SOC 的变化，并且能够有效克服 SOC 初始值不稳定带来的误差，使最大误差保持在 2.0 %以内。

[1] 潘卫华, 刘晓丹. 基于改进卡尔曼滤波的锂电池 SOC 估算研究[J]. 计算机仿真, 2014,31(3)：148-150.

[2] XIONG Rui, GONG Xianzhi, MI Chunting Chris, et al. A robust tate-of-charge estimator for multiple types of lithium-ion batteries using adaptive extended Kalman filter[J]. Journal of Power Sources, 2013, 243：805-816.DOI：10.1016/j.jpowsour.2013.06.076.

[3] 马文伟, 郑建勇, 尤, 等. 应用 Kalman 滤波法估计铅酸蓄电池 SOC[J]. 蓄电池, 2010, 47(1)：19-23.

[4] 毛华夫, 万国春, 汪镭, 等. 基于卡尔曼滤波修正算法的电池 SOC 估算[J]. 电源技术, 2014(2)：298-302.

[5] CHENG K W E, DIVAKAR B P, WU H J, et al.Battery management system (BMS) and SOC development for electrical vehicles [J]. IEEE Trans Veh Technol, 2011, 60(1)：76-88.DOI：10.1109/TVT.2010.2089647.Source：IEEE X plore.

[6] 熊瑞. 基于数据模型融合的电动车辆动力电池组状态估计研究[D]. 北京理工大学, 2014.

[7] 蔡飞, 王顺利. 基于卡尔曼滤波的锂离子蓄电池组 SOC 估算方法研究[J]. 电源世界, 2015, 49(6)：39-41.

[8] 钟国彬, 何耀, 刘新天, 等. 基于高阶非线性模型的铅酸蓄电池 S O C 估计[J].蓄电池, 2015(4)：166-169. DOI：3969/j.issn.1006-0847.2015.04.005.

[9] 张方亮. 基于滤波算法的锂电池 SOC 估算方法对比分析研究[J]. 电源世界, 2016(6)：21-23.