Reduced Sensitivity of Tropical Cyclone Intensity and Size to Sea Surface Temperature in a Radiative-Convective Equilibrium Environment

Shuai WANG and Ralf TOUMI

1 State Key Laboratory of Satellite Ocean Environment Dynamics,Second Institute of Oceanography,Hangzhou 310000,China

2 Space and Atmospheric Physics Group,Department of Physics,Imperial College London,London SW7 2AZ UK

1.Introduction

Tropical cyclones(TCs)are one of the major natural hazards threatening human lives and properties in coastal regions.Although the understanding of TC dynamics and thermodynamics has been much advanced in recent decades(e.g.,Emanuel,1991,1999a;Chan,2005;Montgomery and Smith,2017),it remains challenging to project TC features in a future warming climate(Vecchi et al.,2008;Bender et al.,2010;Knutson et al.,2010;Walsh et al.,2016).

Based on the established TC thermodynamic theories(Emanuel,1986,1995,2003,2007;Holland,1997;Xu and Wang,2010),TC intensity and size are closely related to sea surface temperature(SST).To investigate the response of TC intensity and structure to future sea surface warming,there are two commonly used numerical approaches in idealized and real TC case studies,which will be briefly reviewed below.

As the first approach to understanding the impact of SST on TC intensity and size,SST is changed whereas the initial atmospheric state is held.For example,Lau et al.(2016)found that with the present atmospheric state and a future SST pattern under a double carbon dioxide(CO2)condition,the maximum hourly Power Dissipation Index(Emanuel,2005)of Hurricane Sandy(2012)was more than doubled and the lifetime maximum area measured by the gale-force wind(18 m s−1)could be even tripled.Similar results regarding the intensity and size changes are also found in the case studies by Sun et al.(2017),who modified the present SST with a uniform increase and based on climate model projections.In this approach,TC intensity and size are highly sensitive to sea surface warming.

The second numerical approach is that of starting the TC simulation in the Radiative-Convective Equilibrium(RCE)state,adjusted to various SSTs.Nolan et al.(2007)showed that the RCE state adjusted to a high SST value is more favorable for TC genesis and intensification.However,they found that the lifetime maximum surface wind increased from about 55 m s−1for SST=25◦C to about65 m s−1for SST=30◦C—a change of only about 2%◦C−1.They explained the low sensitivity using the maximum potential intensity(Vpot)theory(Emanuel,1986,1995).However,they did not explore further to find out which term in theVpotcalculation leads to the relatively low sensitivity of intensity to SST under RCE.The sensitivity of TC size to SST under RCE remains unexplored.Chavas and Emanuel(2014)showed that the wind speed of the whole azimuthal gradient wind pro file increased under RCE from low to high SSTs.However,this positive relationship between SST and size was established based on the statistical equilibrium state of cyclones for simulation day 6090,which is an unrealistically long period for real TCs to achieve.

Based on previous studies,TCs show quite different sensitivities of intensity to SST changes with and without a prestorm RCE adjustment.In addition,the size response to SST under RCE within a duration comparable to real TCs remains unclear.We will try to address these two problems in this study using theVpottheory(Emanuel,1995),an analytic TC wind pro file model[the λ model(Wang et al.,2015)],and full-physics idealized numerical simulations with the Advanced Research Weather Research and Forecasting model(Skamarock et al.,2008).

Two main hypotheses will be tested:

(1)Compared to the simulations without the pre-storm RCE adjustment,the pre-storm RCE adjustment reduces the degree of thermodynamic disequilibrium between the air boundary layer and the sea surface,which leads to less sensitivity of both intensity and size to sea surface warming.

(2)The TC response to SST changes in coupled climate model projections is closer to the idealized simulations under RCE.

The next section introduces the model setup,experimental design,theVpottheory and the λ model.The results are presented and discussed in sections 3 and 4.Section 5 summarizes our findings.

2.Method

2.1.RCE adjustment

For the pre-storm RCE adjustment,we conduct a highly idealized simulation with a square domain of 200 km(50×50 grid points),41 vertical layers and grid spacing of 4 km.The RCE adjustmentis conducted over a water-only domain on anf-plane(20◦N,f≈ 5×10−5s−1).Jordan’s(1958)sounding is used as the initial condition and a doubly periodic lateral boundary condition is also applied.Each RCE adjustment lasts for 60 days with a time step of 30 s.The domain setup follows Nolan et al.(2007)and Chavas and Emanuel(2014).Self-aggregation(Bretherton et al.,2005)does not appear in any RCE adjustment run.

All pre-storm RCE adjustment simulations use the following parameterization schemes: the Rapid Radiative Transfer Model scheme(Mlawer et al.,1997)and Dudhia(1989)scheme to estimate the effect of longwave and shortwave radiation;the WSM six-class graupel scheme(Hong and Lim,2006)for microphysical processes;the Yonsei University scheme(Hong and Lim,2006)for parameterization processes in the planetary boundary layer;and the MM5 similarity scheme(Zhang and Anthes,1982)for the surface layer simulation.We remove the diurnal cycle of shortwave radiation for RCE adjustment by keeping the solar zenith angle at 51.7◦and reducing the solar constant to 655 W m−2(Tompkins and Craig,1998a).The precise RCE state may vary with a different solar zenith angle and solar constant,but we will not discuss this in the current study.No cumulus scheme is used for RCE adjustments.

The criterion for RCE is that the potential temperature at each vertical layer below 200 hPa does not change more than 1 K in the next 30 simulation days,which is a similar criterion as used in Chavas and Emanuel(2014).The duration to reach the RCE state may vary with different RCE definition criteria(Tompkins and Craig,1998b).We take the 30-day mean and domain-averaged temperature and moisture vertical pro files after reaching the RCE state as the mean RCE sounding pro file.With SST varying from 26◦C–30◦C,all the RCE adjustments in this work are achieved within 20 simulation days.We therefore take the mean sounding from 20 to 50 simulation days as the sounding pro files in RCE.

An extra zonal wind(Usfc)is added into the surface layer scheme to increase the surface evaporation rate during the RCE adjustment.Nolan et al.(2007)showed that the RCE state mainly depends on two tuning variables,SST andUsfc,and is insensitive to the Coriolis parameter.Chavas and Emanuel(2014)also found that if the tunable parameters in the radiation schemes are simply ignored,SST andUsfcare two main factors affecting the variation of RCE states.In this study,the influence of radiative processes on TCs under RCE will not be investigated.We next focus on SST andUsfcto design experiments.

2.2.Experiment design

Figure 1 shows the mean vertical structures of thermodynamic state for simulation days 20–50 with SST=28◦C andUsfc=1 or 5 m s−1.Due to a stronger surface evaporation rate withUsfc=5 m s−1,the boundary air is more saturated(Fig.1d).High saturation of surface air leads to a weaker moisture contrast with the sea surface and hence a weaker environmental latent heat flux for the following cyclone simulations.As shown in Table 1,there are two groups of simulations in this study.In the first group,Usfcis set as 1 m s−1,corresponding to a relatively high latent heat environment(named Group HL).In the second group,Usfcis set as 5 m s−1,which simulates a relatively low latent heat environment(named Group LL).

Fig.1.Sounding pro files of(a)potential temperature(units:K),(b)temperature(units:K),(c)mixing ratio(units:g kg−1)and(d)relative humidity(units:%),averaged for simulation days 20–50 in the RCE adjustment runs with SST=28◦C,and U sfc=1 m s−1(solid line)or 5 m s−1(dashed line).These two sounding pro files are used as“control runs”in this study.

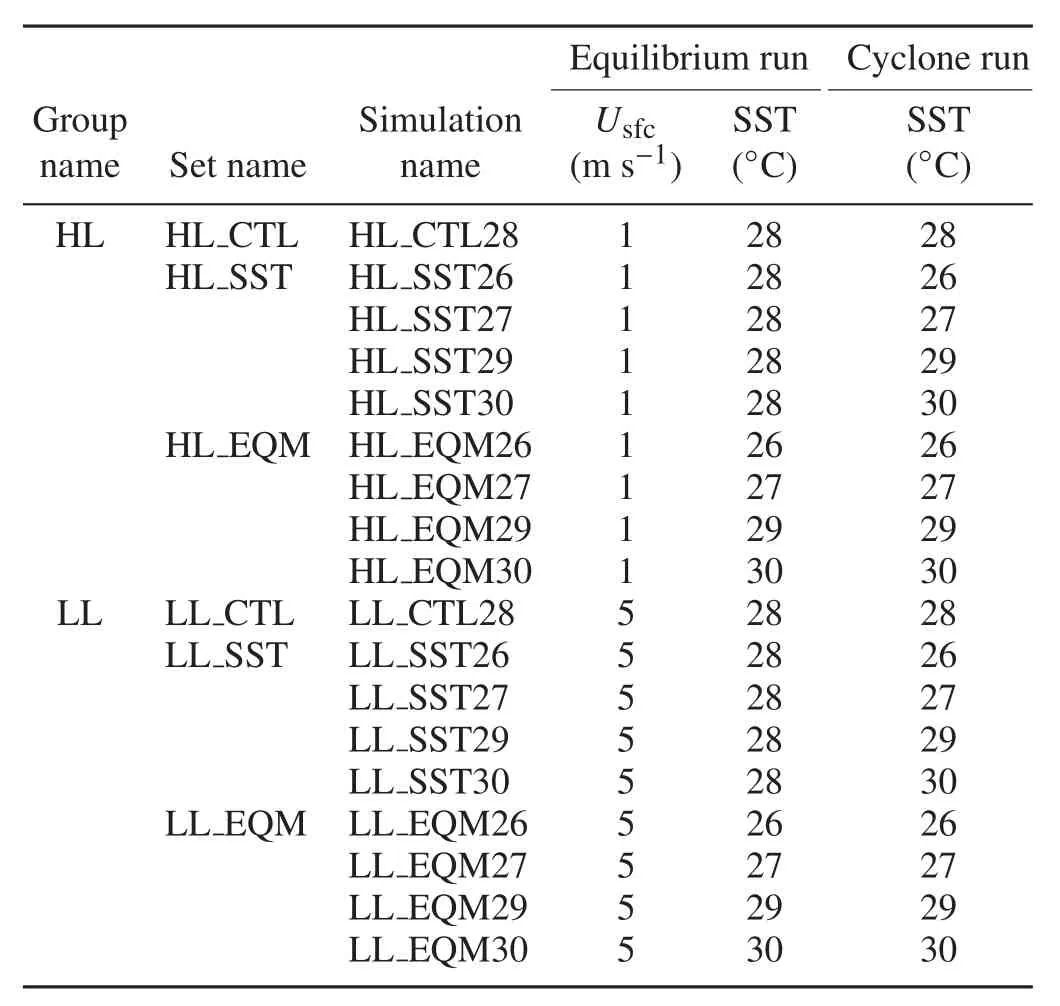
Table 1.Experiment names and descriptions.

In each group,we set SST=28◦C as the control.The control runs in both Group HL and Group LL reach the RCE after about 10 days.Based on the equilibrium states of the control runs,we conduct two sets of sensitivity experiments in each group.For Set HL_SST_and LL_SST(the SST experiments),we change the SST and no further RCE adjustmentis conducted.These experiments are designed to test the sensitivity of TC intensity and size to SST changes in the first approach,as reviewed in section 1.For HL_EQM and LL_EQM[the experiments after the equilibrium(EQM)adjustment],we change the SST and adjust the atmosphere to RCE again.The aim of these two sets of experiments is to test the sensitivity of TC intensity and size to SST changes under RCE,i.e.,the second approach.We use domain-averaged temperature and moisture soundings for simulation days 20–50 to set up the environment for the TC simulations.

2.3.TC simulation setup

The initial field for the TC simulations is set up with different sounding pro files and an initial bogus vortex specified,as in Chan and Williams(1987),with the initial maximum surface wind,radius of maximum wind,and shape parameterbset as 20 m s−1,75 km and 0.7,respectively.Readers are referred to Wang et al.(2015)for more details on inserting the initial vortex and adjusting the thermal and dynamical fields.

The initial cyclone is on a spherical Earth at 20◦N over an open ocean with a fixed SST.Two domains are nested with two-way interaction.There are 41 vertical layers in each domain.The outer square domain has sides of 9000 km and a grid spacing of 15 km.The central latitude of the outer domain is 34◦N.The inner domain has sides of 2400 km and a grid spacing of 3 km.The vortex-following technique is applied for the inner domain.The cyclone is tracked at 800 hPa.The time step for the outer and inner domains is 50 s and 10 s,respectively.Each cyclone simulation lasts for six days.

The lateral boundary condition of the inner domain is fed by the outer domain.The temperature and moisture at the lateral boundary of the outer domain is fixed as the initial sounding pro file.A strong sponge layer with a width of 225 km is added along the lateral boundary of the outer domain.It is implemented by overwriting the horizontal wind speed in both directions to 0 m s−1at all vertical levels and at every time step.The sponge layer reduces the noise level near the boundary so that the TC outer circulation(especially at the upper level)will not be influenced by artificial noise from the environment.At the start of the simulation,the cyclone is 3000 km away from the boundary.Although the circulation expands at the end of the simulation,the cyclone center is still at least 5000 km away from the outer boundary.The β-drift effect is included in the TC simulations but it will not be discussed in this study.

The parameterization schemes for the TC simulations are the same as for the RCE adjustments except that in the former an unmodified shortwave radiation with a diurnal cycle is used to create an Earth-like environment.There is no cumulus scheme in either domain.The inner domain with 3-km grid spacing is capable of resolving convective processes.To reduce the noise level in the surrounding area,the cumulus scheme is not included in the outer domain.Nevertheless,the convection related to the cyclone can still be reasonably simulated in the outer domain because of the two-way interaction and the large coverage of the inner domain.

2.4.V pot and its factors

Vpotcan be defined as(Emanuel,1986,1995)

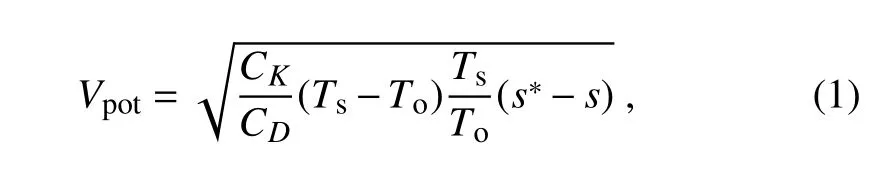
whereC Kis the exchange coefficient for enthalpy,C Dthe drag coefficient,Tothe out flow temperature,Tsthe SST under the eye wall,s∗the saturation entropy of the sea surface,andsthe entropy of the boundary layer air.This expression is the dimensional equivalent of Eq.(13)in Emanuel(1995).

We can decompose the r.h.s.of Eq.(1)into three factors,i.e.,

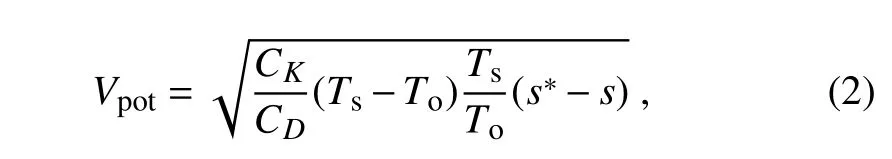
whereC Kis the exchange coefficient for enthalpy,C Dthe drag coefficient,Tothe out flow temperature,Tsthe SST under the eye wall,s∗the saturation entropy of the sea surface,andsthe entropy of the boundary layer air.This expression is the dimensional equivalent of Eq.(13)in Emanuel(1995).

We can decompose the r.h.s.of Eq.(1)into three factors,i.e.,

where

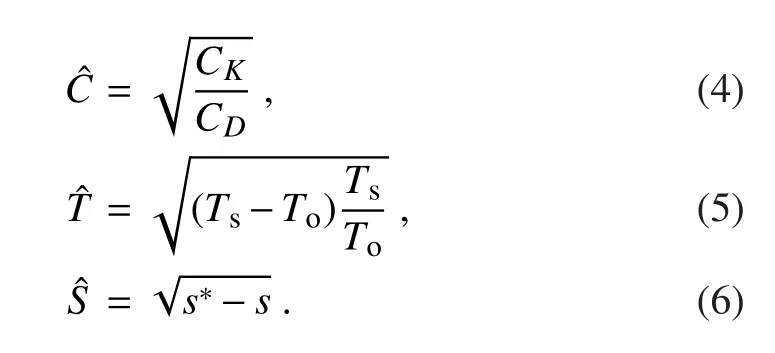
The first factor,,represents the ratio of enthalpy to momentum exchange coefficients and will not be discussed in this study.For simplicity,we set this ratio as 0.9 in the following calculation,which lies in the range 0.75–1.5 for real TCs(Emanuel,1995).The second factor,,describes the vertical temperature contrast.Any change ofcorresponds to the change of the efficiency of the cyclone energy cycle.The third factor,ˆS,can be interpreted as the degree of thermodynamic disequilibrium between the air boundary layer and the sea surface.Any change incan result in different latent heat fluxes at the sea surface.We will show in the results section that the pre-storm RCE adjustment can changeand,and hence influence the cyclone intensity and size.

2.5.Wind pro file

An analytic TC wind pro file model,the λ model(Wang et al.,2015),is used to provide a theoretical estimation of the wind pro file changes due to sea surface warming.The λ model can be written as

whereVis the near-surface wind speed(m s−1); ∆pis the pressure deficit(Pa)between the cyclone center and the ambient environment;ρ is the air density near the surface,which is set as 1.1 kg m−3;ris the radius(m);fois the Coriolis parameter,which is set as 5×10−5s−1(20◦N)in this study;andRmis the radius of maximum wind(m).

The pressure deficit,∆p,in Eq.(6)is calculated with the surface maximum wind speed(Vm)andRm,according to a new wind–pressure relationship(Wang and Toumi,2016,2017):

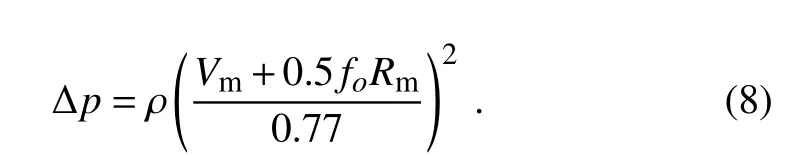
To estimateRmin Eqs.(6)and(7),an empirical relationship used in operational forecasts is adopted(Kna ff and Zehr,2007;Courtney and Kna ff,2009),which can be written as

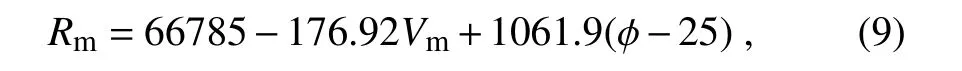
where φ is the latitude of the cyclone center.

The TC destructive potential is measured by the integrated power dissipation(IPD;Emanuel,1999b),which can be written as

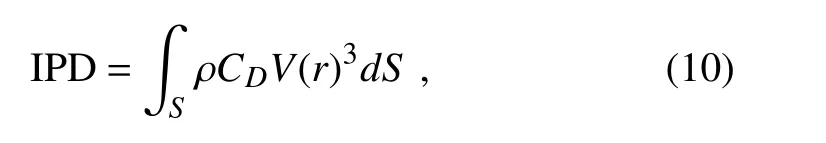
where the drag coefficient,C D,is calculated with the wind speed(Large and Yeager,2008);andSis the integral area with the radius of gale-force wind(R18)at a height of 10 m.The order of magnitude of IPD for a developed TC is typically about 1013W(Emanuel,1999b;Wang and Toumi,2016).

3.Results

3.1.Sensitivity based on theoretical models

TheVpottheory and the λ model are used as theoretical tools to analyze the TC sensitivity to SST changes.As shown in Table 2,the sensitivity of,andVpotare calculated with Eqs.(1)–(5),and the corresponding changes ofR18and IPD are estimated with Eqs.(6)–(9).

First,Table 2 shows that the percentage change(%)of,,Vpot,R18and IPD due to SST changes within a range of 26◦C–30◦C is almost linear in all four sets of experiments,which makes it possible to describe the sensitivities as“%◦C−1”in the following analyses.Second,the sensitivity ofto SST changes are almost identical(about 1%◦C−1–2%◦C−1)in all sets of experiments.In contrast,the sensitivity ofˆSto SST changes depends strongly on the RCE adjustment.For example,the sensitivity ofin RCE is comparable to the sensitivity of,while the difference of the percentage change betweenandis much larger without RCE.Third,the sensitivities ofVpotare about 12%◦C−1and 16%◦C−1without the pre-storm RCE,but only about 3%◦C−1and 3%◦C−1in RCE.It is noteworthy that the intensity response to SST changes under RCE is only about 20%of that in the environment without RCE.

Table 2 also shows that,like the intensity response,the size response to SST changes predicted by the λ model is also much larger without RCE(about 7%◦C−1and 11%◦C−1)than that in RCE(about 2%◦C−1and 2%◦C−1).As a combined metric of intensity and size,IPD changes for 33%◦C−1and 49%◦C−1without RCE,and 9%◦C−1and 8%◦C−1in the RCE experiments.Table 2 suggests that the large difference of TC sensitivity to the same SST change can be attributed to the changes ofby RCE adjustments.We will return to this point later when analyzing the latent heat flux field in numerical simulations.

Figure 2 shows the wind pro file changes predicted by the λ model with various SST values.We can see that the wind pro files in the SST experiments change dramatically(Figs.2a and b).Another important prediction by the λ model is that,regardless of pre-storm RCE adjustments,the wind speed change is always larger in the inner core than the outer rainbands,which indicates a higher sensitivity of the inner core to the sea surface warming than the outer core.

Next,we will conduct full-physics idealized simulations to confirm the different sensitivities of intensity,size and destructive potential to SST changes as found in the theoretical calculations.

3.2.Sensitivity based on idealized simulations

The time series of the surface maximum wind speed,Vm,in four sets of experiments is shown in Fig.3.One can seethat the intensity increases dramatically in the first two simulation days.From simulation hour 48 the intensity fluctuates around some mean value.We therefore identify the first two simulation days as the developing stage,and from simulation hour 48 the simulated cyclone reaches the mature stage.

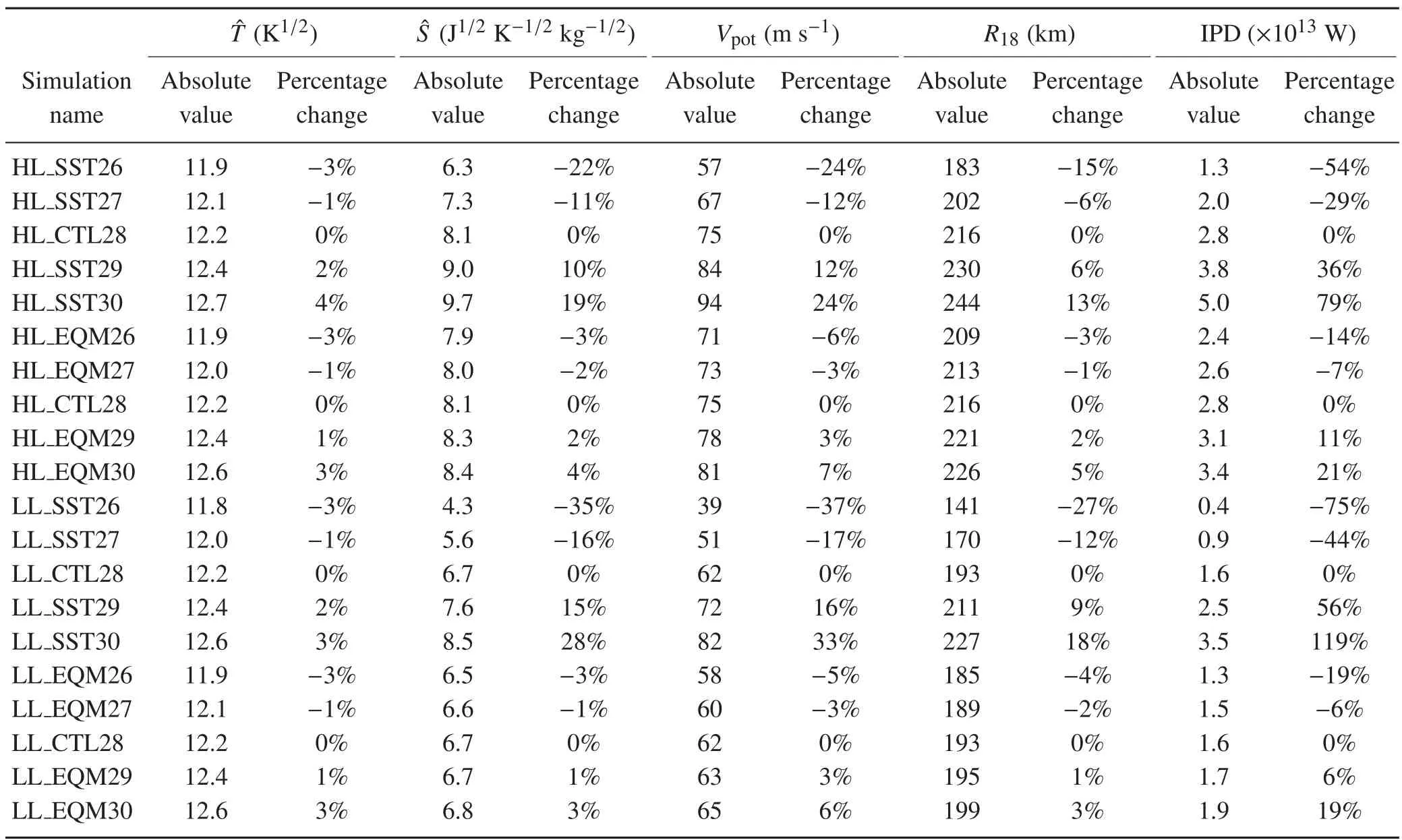
Table 2.Changes inˆT,ˆS and V pot in Eq.(2)based on V pot theory,and changes in R18 and IPD calculated with the λ model wind pro files.

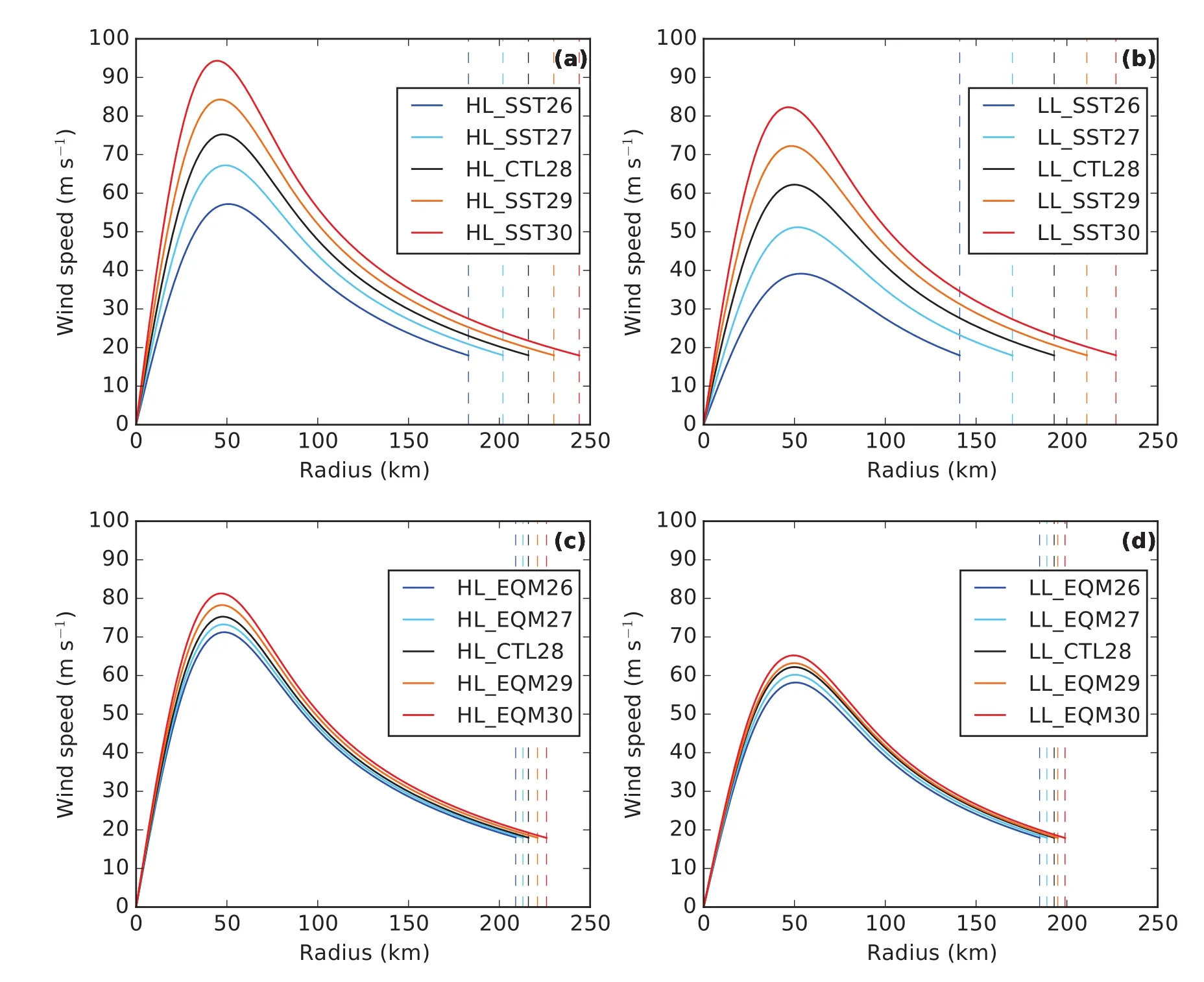
Fig.2.Wind pro files predicted by the λ model for set(a)HL_SST,(b)LL SST,(c)HL_EQM and(d)LL_EQM.The wind pro files are shown up to R18.The dashed lines show R18.

There are two main findings from Fig.3.First,as expected,the environment with high latent heat flux favors TC intensification.However,the average intensity difference between high and low latent heat flux environments is small.For example,the mean intensity in HL_CTL28(Figs.3a and c)during the mature stage is only about 1 m s−1higher than LL_CTL28(Figs.3b and d).Second,compared to the sets with the pre-storm RCE adjustment(Figs.3c and d),the TC intensity without the pre-storm RCE adjustment is more sensitive to SST changes(Figs.3a and b).As shown in Table 3,for example,in a high latent heat flux environment,the sensitivity of TC intensity decreases from 6.5%◦C−1(set HL SST)to 3.6%◦C−1(set HL EQM)if a pre-storm RCE is achieved.

Figure 4 shows the size changes in all four sets of experiments,which are similar to the intensity response shown in Fig.3.Firstly,the cyclone can achieve a large size in a high latent heat flux environment.For instance,R18in HL_CTL28 is450 km atsimulation hour144,whereasitis70 km lowerinLL_CTL28.Secondly,R18is very sensitive to SST changes if the environment is not adjusted to RCE(Figs.4a and b).Table 3 shows that the percentage change ofR18in set HL SST(Fig.4a)and LL SST(Fig.4b)is about 10%◦C−1.However,R18is almost insensitive to SST changes under RCE(Figs.4c and d).

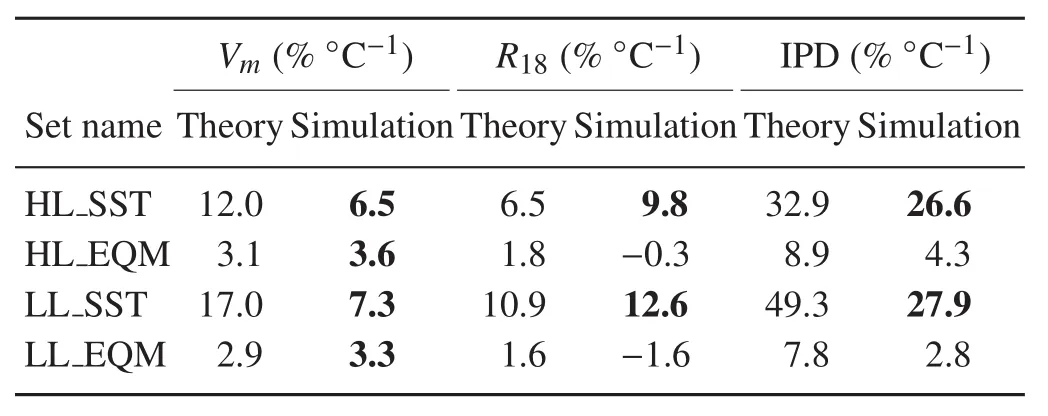
Table 3.Sensitivity(% ◦C−1)of intensity,size and destructive potential based on theoretical predictions and numerical simulations.If the change based on numerical simulations is in bold,it means that all four sensitivity experiments in one set is significantly different from the control run at the 95%con fidence level based on the Student’s t-test.

Fig.3.Time series of simulated 10-m maximum wind(units:m s−1)in set(a)HL_SST,(b)LL_SST,(c)HL_EQM and(d)LL_EQM.

The mean wind pro file for simulation hours 48–144 is shown in Fig.5.Without a pre-storm RCE adjustment,the wind speed of the whole pro file increases with increasing SST(Figs.5a and b).In contrast,if the environment is equilibrated,the changes of wind speed mainly happen in the inner core near the eye wall(Figs.5c and d).These two main findings are qualitatively consistent with the prediction by the λ model(Fig.2),but the absolute sensitivity in the idealized numerical simulations is smaller than the theoretical prediction.

Figure 6 shows the time series of percentage change in the destructive potential measured by IPD.Due to the high sensitivity of intensity and size in the SST experiments,the percentage change of IPD in these two sets is evidently larger than for RCE.Table 3 shows that without the RCE adjustment,SST can significantly change the IPD with a rate of more than 25%◦C−1.On the other hand,if the environment is adjusted to RCE,sea surface warming may still increase the IPD through TC intensification.However,the change of IPD in RCE is not significant.

Table 3 compares the theoretical prediction and numerical simulation regarding the sensitivity of intensity,size and destructive potential.Firstly,we can see that the theoretical and simulated sensitivities of TC intensity are similar under RCE.Secondly,without the pre-storm RCE adjustment,TC size is more sensitive in the simulations than the λ model prediction.Thirdly,regardless of RCE adjustment,the sensitivity of IPD is always less in simulations than theoretically.Table 3 shows that,according to our idealized numerical simulations,only the TC intensity is significantly sensitive to SST changes under RCE.Although the IPD increases with high SSTs in the simulations,this is not found to be significant.

3.3.Sensitivity and latent heat flux

As shown in Table 2,factormay be the main reason that TCs show different sensitivities to SST changes with and without the pre-storm RCE adjustment.FactorˆScan be interpreted as the degree of thermodynamic disequilibrium between the air boundary layer and the sea surface.HighˆSvalues indicate strong latent heat fluxes from the sea surface.We therefore hypothesized in section 1 that different sensitivities of intensity and size with and without pre-storm RCE adjustments are caused by different latent heat fluxes.

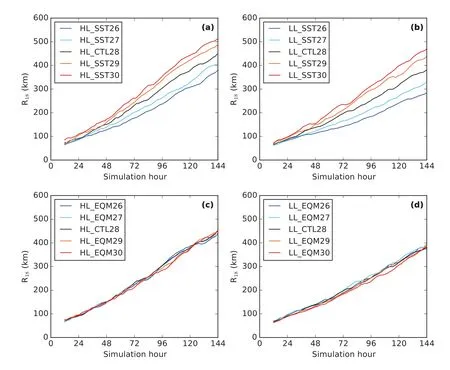
Fig.4.As in Fig.3 but for R18 calculated with the azimuthally averaged 10-m wind pro files.

To examine this hypothesis,the latent heat fluxes at simulation hour 72 is shown in Fig.7.It is found that,regardless of RCE adjustment,the surface latent flux in the inner core is always stronger if SST is higher.Strong latent heat flux under the eye wall can contribute to high intensity.This explains why the intensity is significantly sensitive to SST changes in all four sets of experiments(Table 3).Secondly,without the RCE adjustment(Figs.7a,b,e and f),the latent heat flux is much stronger around the area of gale-force wind in high SST runs than low SST runs.The large size difference is due to this large latent heat flux difference in the outer rainbands.Thirdly,under RCE(Figs.7c,d,g and h),the influence of SST on the local latent heat flux around the area of gale-force wind is much less than the cases without the REC adjustment.This may explain why TC size is less sensitive to SST change for the cases under RCE.

4.Discussion

In this study,we use two factors,and,to quantify the theoretical impact of sea surface warming on TC intensity and size under RCE.We find that,compared to the TC sensitivity without the pre-storm RCE adjustment,TC intensity and size show much lower sensitivity to the same sea surface warming under RCE.The theoretical calculation suggests that a different sensitivity for the same SST change with and without the pre-storm RCE adjustment is due to a reduction ofˆS[Eq.(5))sensitivity in RCE.

The first issue in need of discussion is why bothandare related to intensity and size.FromVpottheory(Emanuel,1986,andare two principal factors affecting TC intensitydescribes the vertical temperature contrast between the sea surface and the out flow layer.Wang et al.(2015)showed that decreasing the temperature in the out flow layer with a fixed SST can increase the TC size,which to some extent shows the linkage between TC size and.The factorcan be interpreted as the degree of thermodynamic disequilibrium between the air boundary layer and the sea surface,which meansis closely related to the enthalpy flux at the sea surface.Xu and Wang(2010)analyzed the contribution of surface enthalpy flux at different radii to TC size.Radu et al.(2014)reported strong sensitivity of TC size to latent heat flux.These studies support the link between TC size and.

Although bothandcan change the TC intensity and size,our results show that onlyis markedly influenced by RCE adjustments(Table 2).If SST increases without RCE adjustment,the saturation specific humidity at the sea surface increases,whereas the air specific humidity at the reference height remains the same.According to the bulk aerodynamic calculation,the latent heat flux is unrealistically increased.This can lead to considerable increases in intensity,size and hence destructive potential(Table 3).If SST increases and at the same time the environment is adjusted towards RCE,the low-level humidity can be increased via surface evapo-ration.The specific humidity contrastis then reduced,which results in a weaker enhancement of latent heat flux than the case without RCE adjustment(e.g.,Fig.7b compared with Fig.7d).However,the change inTsandTodue to RCE adjustments is small compared to their base values,so that the ratio ofTstoTodoes not change much.In addition,we find that RCE adjustments usually shift the whole temperature pro file towards the same direction with a similar magnitude(e.g.,Nolan et al.,2007).Consequently,the change in(Ts−To)due to RCE is alsoˆ small.All the above chˆangeslead to a high sensitivity ofSand low sensitivity ofTwith RCE adjustments.

Our simulations are only based on a limited number of runs,but the sensitivity of TC intensity is in line with previous studies.With a future SST field and the present atmospheric state(i.e.,an example without the pre-storm RCE adjustment),Lau et al.(2016)showed that the maximum hourly Power Dissipation Index of Hurricane Sandy(2012)can be increased by 100%–160%,which corresponds to an increase of about 26%–38%in the surface maximum wind speed.The SST change between present and future states along the track of Hurricane Sandy(2012)in Lau et al.(2016)is about 2◦C.This simple calculation leads to a sensitivity of intensity to sea surface warming of 15%◦C−1.This value is within the range of our theoretical calculation,as shown in Table 3(12%◦C−1in set HL_SST and 17% ◦C−1in set LL_SST).As an example with the pre-storm RCE adjustment,Nolan et al.(2007)showed that the sensitivity of intensity to SST changes under RCE is only about 2%◦C−1,which is also close to the theoretical and numerical estimations in Table 3(2.9%◦C−1to 3.6%◦C−1).

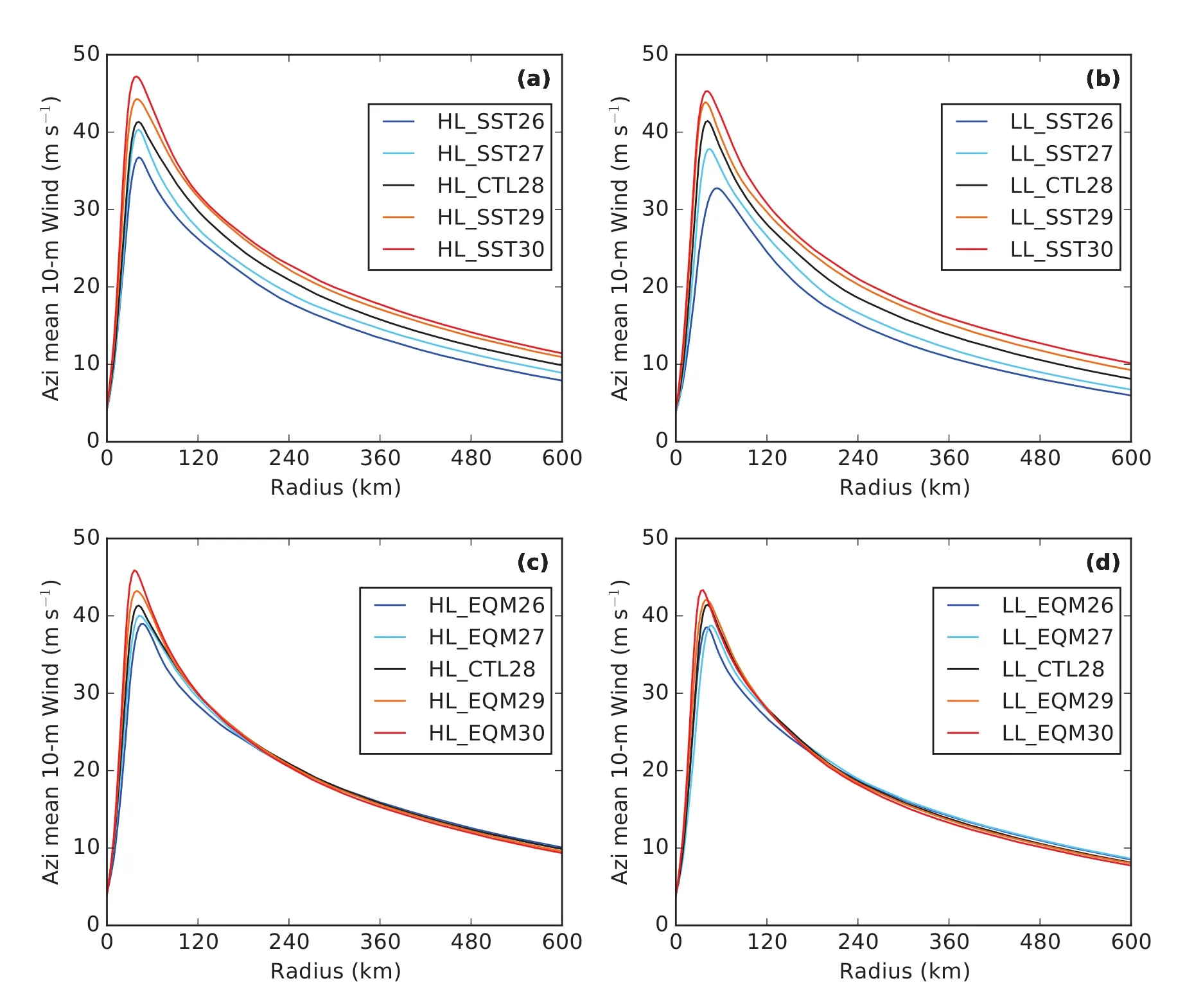
Fig.5.Azimuthally averaged 10-m wind pro file during the mature stage in set(a)HL SST,(b)LL_SST,(c)HL_EQM and(d)LL_EQM.

One may question whether the TC sensitivity with RCE adjustment is more realistic in a warming climate.An SST increase without any RCE adjustment is impossible.The time scale for the large-scale sea surface warming can be decades,and it is much longer than the time scale of RCE,which is of the order of tens of days.However,a perfect RCE may rarely exist in the tropics,because of large-scale circulations(Manabe and Strickler,1964).As discussed in previous studies(Bretherton et al.,2005;Nolan et al.,2007),the RCE state shares certain features of the tropics but is still idealized.In this regard,our sensitivity experiments with and without the pre-storm RCE adjustments may simulate two extreme situations.To find out which situation is closer to the sensitivity of real TCs in a warming climate,we can compare our results with the predictions by climate models.

By simulating idealized TCs with the atmospheric temperature and moisture pro files and SSTs from coupled climate models,Knutson and Tuleya(2004)found that the maximum surface wind increased by about 6%as a response to a 1.75◦C CO2-induced tropical sea surface warming.If we assume the intensity response in their study is also linear,that corresponds to an intensity sensitivity of 3.4%◦C−1.Knutson et al.(2015)showed that the sensitivity of TC intensity to sea surface warming is 2.9%◦C−1,4.6%◦C−1and 3.5%◦C−1in the North Atlantic,eastern North Pacific and western North Pacific,respectively,with a mean of 3.7%◦C−1.A more recent study(Yoshida et al.,2017)found that the lifetime maximum intensity of global TCs may increase by 9%with an average sea surface warming of 3◦C–3.2◦C in the tropics.Their finding therefore also suggests an intensity sensitivity of about 3%◦C−1.The intensity sensitivity found in Knutson and Tuleya(2004),Knutson et al.(2015)and Yoshida et al.(2017)is consistent with our numerical simulations under RCE(Table 3).

This agreement on the intensity sensitivity by climate models and our RCE simulations suggests that the intensity trend in those climate model projections can be considered as largely due to the thermodynamic response in RCE,and thus any changes in large-scale dynamics,such as vertical wind shear,are minor contributors in those climate model projections.Despite this generalization,there could be regional differences,as dynamic factors are important controls on TC intensity and structure.For example,Wang and Toumi(2016)showed that the variation of both IPD and Power Dissipation Index of US land falling hurricanes can be largely explained by the vertical wind shear in the main genesis area,and Vecchi and Soden(2007)reported a tropical Atlantic wind shear increase in their climate projections.

Regarding the size change,most climate models are unable to project a trend due to low spatial resolution.However,with a coupled dynamical downscaling approach,Knutson et al.(2015)could simulate a reasonable distribution of global TC size.They found that in a warming future,there will be fewer TCs in total,with a general increase in the lifetime maximum wind,but almost no change in the global mean size.This low sensitivity of TC size to SST change agrees well with our simulations under RCE(Table 3).Furthermore,Emanuel(2005)showed a sharp increase in the Power Dissipation Index of the North Atlantic TCs after 1980 with an increase of SST.However,no similar trend in the observed TC size was found during that period(Kna ff et al.,2014).These studies suggest that the response of TC intensity and size to sea surface warming in an idealized RCE environment is in agreement with the coupled climate models and observations.

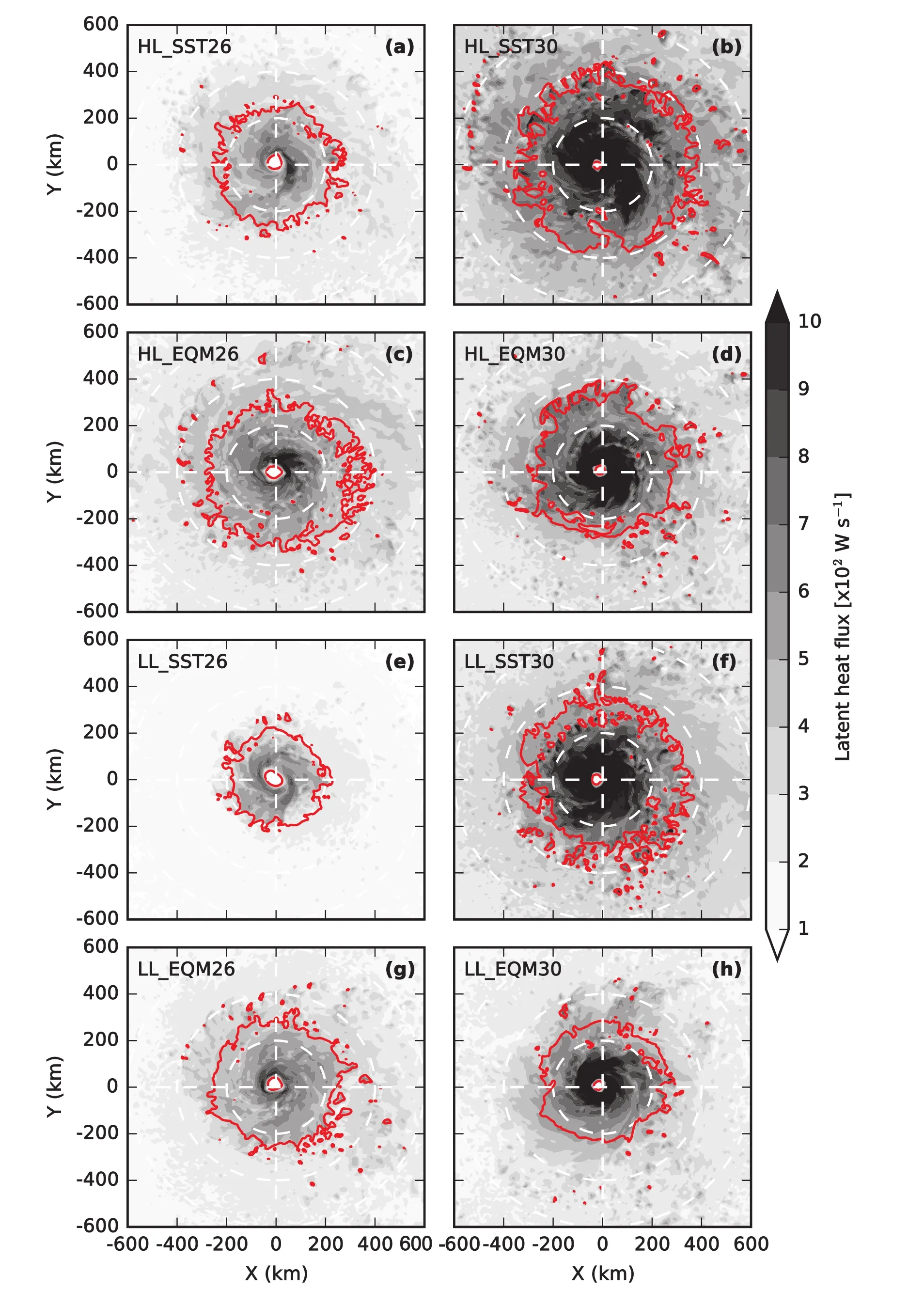
Fig.7.Latent heat flux(shading;units:102 W s−1)at simulation hour 72 in simulation(a)HL_SST26,(b)HL_SST30,(c)HL_EQM26,(d)HL_EQM30,(e)LL_SST26,(f)LL_SST30,(g)LL_EQM26 and(h)LL_EQM30.The red contours show the isotachs of gale-force wind(18 m s−1)at a height of 10 m.Three circles(white dashed lines)are placed at radii of 200,400 and 600 km from the TC center.

5.Conclusions

In this study we have compared the sensitivities of TC intensity,size and destructive potential to SST changes with and without a pre-storm RCE adjustment.We find that TCs show relatively low sensitivity to sea surface warming under RCE.This is because the RCE adjustment reduces the degree of thermodynamic disequilibrium between the air boundary layer and the sea surface,which leads to less surface latent heat flux than without any RCE adjustment.

We find that the sensitivity of TC intensity is about 3%◦C−1–4%◦C−1in RCE.Our results also show that the TC size is insensitive to SST change in RCE.As a combined metric of intensity and size,IPD changes are not significant.Without any RCE adjustment,regional TC model studies are likely to show unrealistically large responses to SST perturbations.The sensitivity of TC intensity and size under RCE in our simulations is consistent with projections by climate models.This suggests that first-order projected global changes in TC intensity are driven by thermodynamics not dynamics.

Acknowledgements.This work and its contributors were supported by the UK–China Research&Innovation Partnership Fund through the Met Office Climate Science for Service Partnership China as part of the Newton Fund.SW was also supported by the National Natural Science Foundation of China(Grant No.41706007),China Postdoctoral Science Foundation(Grant No.2017M611960)and the National Programme on Global Change and Air–Sea Interaction(Grant No.GASI-IPOVAI-04).

Open AccessThis article is distributed under the terms of the Creative Commons Attribution License which permits any use,distribution,and reproduction in any medium,provided the original author(s)and the source are credited.

REFERENCES

Bender,M.A.,T.R.Knutson,R.E.Tuleya,J.J.Sirutis,G.A.Vecchi,S.T.Garner,and I.M.Held,2010:Modeled impact of anthropogenic warming on the frequency of intense Atlantic hurricanes.Science,327,454–458,https://doi.org/10.1126/science.1180568.

Bretherton,C.S.,P.N.Blossey,and M.Khairoutdinov,2005:An energy-balance analysis of deep convective self-aggregation above uniform SST.J.Atmos.Sci.,62,4273–4292,https://doi.org/10.1175/JAS3614.1.

Chan,J.C.L.,2005:The physics of tropical cyclone motion.Annual Review of Fluid Mechanics,37,99–128,https://doi.org/10.1146/annurev. fluid.37.061903.175702.

Chan,J.C.L.,and R.T.Williams,1987:Analytical and numerical studies of the beta-e ff ect in tropical cyclone motion.Part I:Zero mean flow.J.Atmos.Sci.,44,1257–1265,https://doi.org/10.1175/1520-0469(1987)044<1257:AANSOT>2.0.CO;2.

Chavas,D.R.,and K.Emanuel,2014:Equilibrium tropical cyclone size in an idealized state of axisymmetric radiative–convective equilibrium.J.Atmos.Sci.,71,1663–1680,https://doi.org/10.1175/JAS-D-13-0155.1.

Courtney,J.,and J.A.Kna ff,2009:Adapting the Kna ff and Zehr wind-pressure relationship for operational use in Tropical Cyclone Warning Centres.Australian Meteorological and Oceanographic Journal,58,167–179,https://doi.org/10.22499/2.5803.002.

Dudhia,J.,1989:Numerical study of convection observed during the winter monsoon experiment using a mesoscale two dimensional model.J.Atmos.Sci.,46,3077–3107,https://doi.org/10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2.

Emanuel,K.,2003:Tropical cyclones.Annual Review of Fluid Mechanics,31,75–104,https://doi.org/10.1146/annurev.earth.31.100901.141259.

Emanuel,K.,2005:Increasing destructiveness of tropical cyclones over the past 30 years.Nature,436,686–688,https://doi.org/10.1038/nature03906.

Emanuel,K.,2007:Environmental factors affecting tropical cyclone power dissipation.J.Climate,20,5497–5509,https://doi.org/10.1175/2007JCLI1571.1.

Emanuel,K.A.,1986:An air-sea interaction theory for tropical cyclones.Part I:Steady-state maintenance.J.Atmos.Sci.,43,585–605,https://doi.org/10.1175/1520-0469(1986)043<0585:AASITF>2.0.CO;2.

Emanuel,K.A.,1991:The theory of hurricanes.Annual Review of Fluid Mechanics,23,179–176,https://doi.org/10.1146/annurev. fl.23.010191.001143.

Emanuel,K.A.,1995:Sensitivity of tropical cyclones to surface exchange coefficients and a revised steady-state model incorporating eye dynamics.J.Atmos.Sci.,52,3969–3976,https://doi.org/10.1175/1520-0469(1995)052<3969:SOTCTS>2.0.CO;2.

Emanuel,K.A.,1999a:Thermodynamic control of hurricane intensity.Nature,401,665–669,https://doi.org/10.1038/44326.

Emanuel,K.A.,1999b:The power of a hurricane:An example of reckless driving on the information superhighway.Weather,54,107–108,https://doi.org/10.1002/j.1477-8696.1999.tb06435.x.

Holland,G.J.,1997:The maximum potential intensity of tropical cyclones.J.Atmos.Sci.,54,2519–2541,https://doi.org/10.1175/1520-0469(1997)054<2519:TMPIOT>2.0.CO;2.

Hong,S.-Y.,and J.-O.J.Lim,2006:The WRF Single-Moment 6-class microphysics scheme(WSM6).Asia-Pacific Journal of Atmospheric Sciences,42,129–151.

Jordan,C.L.,1958:Mean soundings for the West Indies Area.J.Meteor.,15,91–97,https://doi.org/10.1175/1520-0469(1958)015<0091:MSFTWI>2.0.CO;2.

Kna ff,J.A.,and R.M.Zehr,2007:Reexamination of tropical cyclone wind–pressure relationships.Wea.Forecasting,22,71–88,https://doi.org/10.1175/WAF965.1.

Kna ff,J.A.,S.P.Longmore,and D.A.Molenar,2014:An objective satellite-based tropical cyclone size climatology.J.Climate,27,455–476,https://doi.org/10.1175/JCLI-D-13-00096.1.

Knutson,T.R.,and R.E.Tuleya,2004:Impact of CO2-induced warming on simulated hurricane intensity and precipitation:Sensitivity to the choice of climate model and convective parameterization.J.Climate,17,3477–3495,https://doi.org/10.1175/1520-0442(2004)017<3477:IOCWOS>2.0.CO;2.

Knutson,T.R.,J.J.Sirutis,M.Zhao,R.E.Tuleya,M.Bender,G.A.Vecchi,G.Villarini,and D.Chavas,2015:Global projections of intense tropical cyclone activity for the late twenty- first century from dynamical downscaling of CMIP5/RCP4.5 scenarios.J.Climate,28,7203–7224,https://doi.org/10.1175/JCLI-D-15-0129.1.

Knutson,T.R.,and Coauthors,2010:Tropical cyclones and climate change.Nature Geoscience,3,157–163,https://doi.org/10.1038/ngeo779.

Large,W.G.,and S.G.Yeager,2008:The global climatology of an interannually varying Air–sea flux data set.Climate Dyn.,33,341–364,https://doi.org/10.1007/s00382-008-0441-3.

Lau,W.K.M.,J.J.Shi,W.K.Tao,and K.M.Kim,2016:What would happen to Superstorm Sandy under the influence of a substantially warmer Atlantic Ocean?Geophys.Res.Lett.,43,802–811,https://doi.org/10.1002/2015GL067050.

Manabe,S.,and R.F.Strickler,1964:Thermal equilibrium of the atmosphere with a convective adjustment.J.Atmos.Sci.,21,361–385,https://doi.org/10.1175/1520-0469(1964)021<0361:TEOTAW>2.0.CO;2.

Mlawer,E.J.,S.J.Taubman,P.D.Brown,M.J.Iacono,and S.A.Clough,1997:Radiative transfer for inhomogeneous atmospheres:RRTM,a validated correlated-k model for the long wave.J.Geophys.Res.,102,16 663–16 682,https://doi.org/10.1029/97JD00237.

Montgomery,M.T.,and R.K.Smith,2017:Recent developments in the fluid dynamics of tropical cyclones.Annual Review of Fluid Mechanics,49,541–574,https://doi.org/10.1146/annurev-fluid-010816-060022.

Nolan,D.S.,E.D.Rappin,and K.A.Emanuel,2007:Tropical cyclogenesis sensitivity to environmental parameters in radiative-convective equilibrium.Quart.J.Roy.Meteor.Soc.,133,2085–2107,https://doi.org/10.1002/qj.170.

Radu,R.,R.Toumi,and J.Phau,2014:Influence of atmospheric and sea surface temperature on the size of hurricaneCatarina.Quart.J.Roy.Meteor.Soc.,140,1778–1784,https://doi.org/10.1002/qj.2232.

Skamarock,W.C.,and Coauthors,2008:A description of the advanced research WRF version 3.NCAR Tech.Note NCAR/TN-475+STR,113 pp,https://doi.org/10.5065/D68S4MVH.

Sun,Y.,and Coauthors,2017:Impact of ocean warming on tropical cyclone size and its destructiveness.Scientific Reports,7,8154,https://doi.org/10.1038/s41598-017-08533-6.

Tompkins,A.M.,and G.C.Craig,1998a:Radiative–convective equilibrium in a three-dimensional cloud-ensemble model.Quart.J.Roy.Meteor.Soc.,124,2073–2097,https://doi.org/10.1002/qj.49712455013.

Tompkins,A.M.,and G.C.Craig,1998b:Time-scales of adjustment to radiative-convective equilibrium in the tropical atmosphere.Quart.J.Roy.Meteor.Soc.,124,2693–2713,https://doi.org/10.1002/qj.49712455208.

Vecchi,G.A.,and B.J.Soden,2007:Increased tropical Atlantic wind shear in model projections of global warming.Geophys.Res.Lett.,34,L08702,https://doi.org/10.1029/2006 GL028905.

Vecchi,G.A.,K.L.Swanson,and B.J.Soden,2008:Whither hurricane activity?Science,322,687–689,https://doi.org/10.1126/science.1164396.

Walsh,K.J.E.,and Coauthors,2016:Tropical cyclones and climate change.Wiley Interdisciplinary Reviews:Climate Change,7,65–89,https://doi.org/10.1002/wcc.371.

Wang,S.,and R.Toumi,2016:On the relationship between hurricane cost and the integrated wind profile.Environmental Research Letters,11,114005,https://doi.org/10.1088/1748-9326/11/11/114005.

Wang,S.,and R.Toumi,2017:A historical analysis of the mature stage of tropical cyclones.International Journal of Climatology,https://doi.org/10.1002/joc.5374.(in press)

Wang,S.,R.Toumi,A.Czaja,and A.Van Kan,2015:An analytic model of tropical cyclone wind pro files.Quart.J.Roy.Meteor.Soc.,141,3018–3029,https://doi.org/10.1002/qj.2586.

Xu,J.,and Y.Q.Wang,2010:Sensitivity of tropical cyclone innercore size and intensity to the radial distribution of surface entropy flux.J.Atmos.Sci.,67,1831–1852,https://doi.org/10.1175/2010JAS3387.1.

Yoshida,K.,M.Sugi,R.Mizuta,H.Murakami,and M.Ishii,2017:Future changes in tropical cyclone activity in high-resolution large-ensemble simulations.Geophys.Res.Lett.,44,9910–9917,https://doi.org/10.1002/2017GL075058.

Zhang,D.L.,and R.A.Anthes,1982:A high-resolution model of the planetary boundary layer—sensitivity tests and comparisons with SESAME-79 data.J.Appl.Meteor.,21,1594–1609,https://doi.org/10.1175/1520-0450(1982)021<1594:AHRMOT>2.0.CO;2.