基于相位差的子区交通信号协调优化控制

胡海涛，罗 杰

(南京邮电大学 自动化学院，江苏 南京 210046)

0 引 言

城市交通系统是现代城市发展的基础[1]，城市交通控制是现代城市智能交通系统的一个重要组成部分。随着智能交通技术的深入研究，区域交通的协调控制已经成为一个研究热点[2-3]。Preethi等针对Webster延迟模型直接应用于非均匀车流以及不规则的道路结构导致的延迟计算不准确的问题，提出一种非均衡车流不规则道路条件下信号交叉口延迟模型，并运用人工神经网络算法验证了模型的有效性[4]。Zhang等针对不同区域路网结构特点，提出一种基于线性拟合法改进Webster延迟模型，提高了延迟时间评估准确性，并运用改进型粒子群算法获得模型最优解[5]。

Zang等结合实际交叉口地理特征和区域交通流数据，采用HCM2000延误计算方法，建立了一种基于子区域交通流优化的交叉口信号控制模型,并运用遗传算法获得了模型最优解[6]。现有的这些研究工作，都是通过构建交通模型，采用智能算法优化控制，在一定程度上提高了交通效率。但以上相关研究仍存在一些问题：如区域协调优化控制模型未充分利用子区内相位差的协调；采用的优化算法的优化效果有待进一步提高等。

基于Webster延迟模型[7]，融入了相位差协调控制机制，文中提出了一种改进型车辆延误计算模型，并运用遗传粒子群混合算法实现子区交通信号协调优化控制。先将路网子区交通流分为子区内部路口交通流和边缘路口交通流两部分[8]，通过引入相位差协调机制，从而将整个路网子区内所有交叉口关联起来；结合改进型车辆延误模型，以子区内车辆的平均时延最短作为优化目标，建立了基于相位差的子区交通信号协调控制模型，并通过仿真进行验证。

1 区域交通信号优化控制模型

目前,大多数城市交通网络交叉口的形状都是“+”型,而右转车辆在交通控制系统上可以不考虑。因此，采用以四个交叉口组成的小区域作为研究对象，忽略车辆右转弯，使用普遍的四相位六车道交通模型。以子区内所有车辆平均延误最小为目标，建立子区交通信号协调控制优化模型。提出的模型主要考虑交叉口的周期、各个交叉口相位时间、相邻交叉口之间的相位差。

1.1 车辆平均延误计算方法

车辆行驶过程中延误能有效反映车辆行驶过程中受到的堵塞状况、行驶时间等交通指标。对此，国内外学者投入了大量研究。截至目前，在交通信号配时优化设计中，英国TRRL的Webster算法是普遍采用的一种计算延迟方法[9]。但Webster延迟模型未将相位差协调机制考虑在内，从而导致子区内部交叉口入口车辆延迟计算不够准确，进而影响交通信号合理分配。文中基于该模型对其进行改进，即融入相位差协调机制，建立了子区内所有车辆延迟模型来估计车辆平均延迟。

由Webster延迟模型计算方法，每一车道上车辆平均延迟时间为：

(1)

其中，d为每辆车平均时延；T为信号周期时长；λ为绿信比；q为交通流量；x为饱和度。式1第一项为车辆均匀到达所产生的延误；第二项为车辆随机到达产生的延误；第三项是根据英国道路情况研究模拟出来的，不具有普遍性，文中不考虑。

1.2 基于相位差的改进延迟模型

通过分析子区路网，根据交通流处于入口和路网内部，将子区路网分为边界交通流和中间交通流。以一个4交叉路口所组成的子区为例，四交叉路口区域路网如图1所示。

图1 四交叉路口区域路网

边界路口为①，②，…，⑧,不需要考虑相位差的影响，而路口a与b、a与c、c与d、b与d之间则需要考虑相位差的影响。故将整个子区延迟分为两种情况：区域外部交叉口延迟和区域内部交叉口入口延迟。

1.2.1 子区外部进口道延迟

子区外部进口道车辆延迟，指的是外部入口车道车流进入区域时，由于在交叉口信号配时问题形成车辆排队而造成的延迟。边界路口车流到达交叉口时可以看成随机到达，符合Webster延迟模型，故直接使用Webster提供的延迟模型。

dout=d

(2)

1.2.2 子区内部进口道延迟

子区内部进口道车辆延迟，指的是进口道处于区域内部的交叉口，车流到达下游交叉口排队造成的延迟。由于内部交通流是按照车队形式到达下游交叉口的，其延迟计算需要整体考虑。

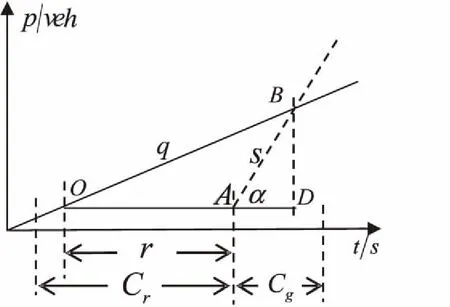
图2 内部交叉口车辆延误

当在任何给定的信号周期中若车辆到达率和路段饱和流量是固定的，则延迟和到达率之间存在线性关系。如图2所示，x轴表示时间，y轴表示车辆总数，q表示车流量，s表示饱和流，T表示周期，Cr表示红灯时间，Cg表示绿灯时间，r表示车队到达下游交叉口j，直到下游交叉口j红灯结束时间，三角形OAB在x轴上的投影表示每辆车辆到达停车线后的延迟，三角形OAB在y轴上的投影表示在不同时刻车辆在停车线后的排队数目。因此，在任何给定的信号周期T(s)中，内部进口道所有到达车辆的相位延迟近似等于三角形OAB面积[10]。

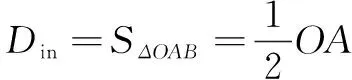
(3)

其中：OA=r,BD=AD*tanα=AD*s。

又由于：

AD*s=(r+AD)*q

AD=qr/(s-q)

即：

(4)

对于内部路口交通流，考虑加入相位差协调控制[11-12]。相位差是指相邻的两个交叉路口，协调相位的开始时间的差值。在子区内，先选定参考交叉口，其余交叉路口协调相位差开始时间以参考交叉路口为基准。同时，相位差的约束需要考虑协调相位的上行和下行，如图3所示。

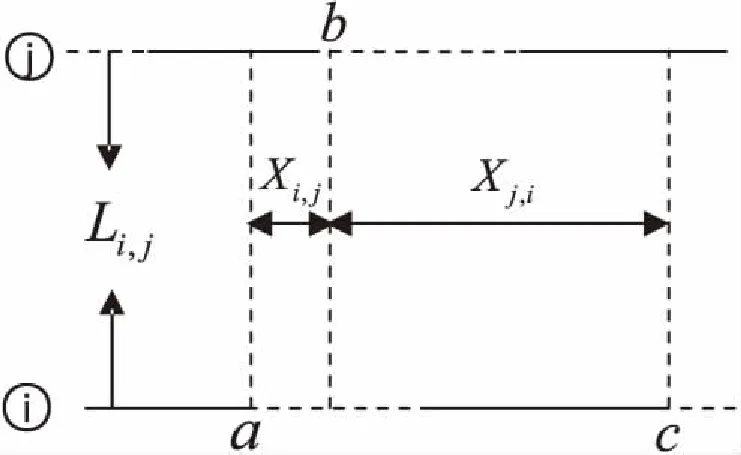
图3 相邻交叉口相位差示意图

其中实线为红灯相位时间，虚线为绿灯相位时间,设Xi,j为上行相位差，Xj,i为下行相位差。故相邻交叉路口在协调相位方向上，上行和下行两个方向上的协调相位差符合相位差闭合条件。即：

0≤Xi,j≤Ci,i,j∈Ncross

Xi,j+Xj,i=n*Ci

其中，n为整数；Ncross为子区中交叉口数目。图3就是n=1时的相位差情况，即两路口为相邻路口。

如图1所示，假设2个交叉口a与b，其中a与b之间距离为L,平均车速为v,θa,b表示交通流从a到b时交叉口的下行相位差，以直行相位为协调相位。

则有：

与式4结合得：

(5)

依据上文提出的延迟模型，设在整个优化时段包含Nc个周期，以四个交叉口组成的子区为分析对象，以所分析的子区内所有机动车流的平均延迟最小为优化目标，建立子区交通信号协调控制优化模型:

(6)

其中，PI表示优化模型目标函数；di,j,k表示子区内第i个交叉口第j相位第k个交通流的车辆平均延迟时间；Fi,j,k表示第i个交叉口第j相位第k个交通流的流量；Ncross为子区交叉口数目；Ni,phase为交叉口相位数；Gri,j为第i个交叉口第j相位的绿灯时间。同时由实际交通情况，取子区内关键交叉口周期作为整个子区信号周期，每个交叉口实际周期长度应在60～240 s之间，各相位需保证最小绿灯时间Grmin,i,j。

2 基于遗传粒子群混合算法子区协调优化控制

2.1 遗传粒子群混合算法

遗传算法(genetic algorithm，GA)具有较强的全局搜索能力，但容易陷入局部最优解[13]。粒子群优化算法(particle warm optimization,PSO)本质为一种随机搜索算法，具有局部搜索能力强[14]、收敛速度快等优点，但PSO全局搜索能力不如GA。将GA和PSO两种算法相结合[15]，可起到互补的效果，即遗传算法可从种群多样性角度来规避算法早熟收敛，粒子群算法则可避免变异算子的随机性和盲目性，从而提高算法收敛效率，使优化结果更加理想。

遗传粒子群混合算法步骤如下：

Step1:种群规模为N，初始化种群中粒子的速度和位置，搜索种群中粒子个体极值点Pi和群体极值点Pg。

Step2:根据式7更新粒子的速度和位置。

(7)

其中，w为惯性权重；vi=(vi,1,vi,2,…,vi,N)为粒子速度；c1,c2为学习因子；r1,r2为分布在[0,1]区间的随机数；j为迭代次数；Pi=(Pi,1,Pi,2,…,Pi,N)为个体极值；Pi=(Pg,1,Pg,2,…,Pg,N)为种群群体极值。

为了避免粒子群优化算法在全局最优解附近出现“震荡”现象，现对w做如下改进：

(8)

其中，wstart=0.9，为初始惯性权重；wend=0.9，为迭代到最大次数时的惯性权重；k为当前迭代次数；Tmax为最大迭代次数。

Step3:计算种群粒子适应度值，判断是否满足终止条件。若满足则终止迭代，输出最优解，否则继续步骤4。

Step4:对适应度值进行排序，选择适应度值靠后的个体，对它们进行交叉操作，得到M个新个体。

交叉操作：通过将个体染色体交换组合，把父代优秀特性遗传给子代，由个体采用实数编码，故交叉操作采用实数交叉法，染色体ak与al在j位交叉操作方法为：

Step5:对所有N个个体执行变异操作，在N+M个个体中按适应度再次排序，选择适应度值高的N个个体进入下一代，转步骤2。

变异操作：为了保证种群多样性，第i个个体第j个基因ai,j发生变异操作的方法为：

其中，f(g)=r2(1-g/Gmax)2，r2为随机数，g为当前迭代次数，Gmax为最大迭代次数；amax为基因ai,j的上界，amin为基因ai,j的下界；r为[0,1]之间的随机数。

2.2 基于遗传粒子群混合算法的子区协调优化

基于上文的描述，得到的子区协调优化控制算法流程如图4所示。

图4 子区协调优化控制算法流程

文中以路网中车辆通过子区的平均延迟最小为优化目标，通过对子区内各交叉口各自绿信时间、信号周期和交叉口间相位差进行优化来达到子区协调优化控制的目的。

子区协调优化控制算法在目标函数选择上，有两种情况：传统的车辆延迟计算模型(Webster)，即式1；融入相位差协调机制后，对子区交通流分为外部和内部进口道延迟计算模型，即式6。

3 仿真实验

3.1 实验参数配置

以一个由四交叉路口组成的区域作为模拟区域进行仿真实验，其中包括12条路段。路段9、10、11、12距离均为300 m，如图1所示。

现针对Webster延迟模型和改进Webster延迟模型，应用遗传粒子群混合算法进行仿真优化，优化过程中的目标函数以及算法适应度函数均为式1和式6。GA-PSO混合算法基本参数如下：交叉概率0.8，变异概率0.01，进化代数500，种群规模100。区域交通约束数据如下：最大信号周期180 s，最小信号周期70 s，最小相位时间15 s，最大相位时间50 s，每车道饱和流量为1 800 veh/h，车辆平均行驶速度40 km/h。结合图1，区域路网交通参数为：路口1，直行679 veh/h，左转269 veh/h；路口2，直行874 veh/h，左转315 veh/h；路口3，直行506 veh/h，左转260 veh/h；路口4，直行302 veh/h，左转170 veh/h；路口5，直行450 veh/h，左转416 veh/h；路口6，直行850 veh/h，左转186 veh/h；路口7，直行363veh/h，左转270 veh/h；路口8，直行335 veh/h，左转233 veh/h。

3.2 两种延迟模型实验对比

实验1：采用Webster延迟模型并结合GA-PSO混合算法对子区协调控制系统建立优化模型；

实验2：采用改进Webster延迟模型并结合GA-PSO混合算法对子区协调控制系统建立优化模型。

实验结果分别如表1和表2所示。

表1 Webster延迟模型及其优化配时结果

在两种延迟模型下子区交通信号协调优化控制，当不考虑相位差进行协调控制时，子区内车辆平均延时为29.1 s，而加入相位差进行子区协调优化控制时，子区内车辆平均延时为21.8 s。实验表明，基于相位差协调的改进Webster延迟模型得到的配时控制方案，相较于传统Webster延迟模型下的配时方案，其子区内车辆平均延时降低了7.3 s，模型性能指标优化效果提升了25.1%。

表2 改进Webster延迟模型及其优化配时结果

4 结束语

将路网子区中的交叉口分为边界交叉口和内部交叉口，提出了一种基于相位差的改进Webster延迟模型。以子区内车辆平均延迟最小为优化目标，采用GA-PSO混合算法进行优化，实现将子区内的所有交叉口信号按相位差进行协调优化控制。仿真实验表明，所提出的改进型延迟优化模型及协调控制方法，能明显降低区域路网的平均车辆延误。

参考文献：

[1] TIAN Bin,MORRIS B T,TANG Ming,et al.Hierarchical and networked vehicle surveillance in ITS:a survey[J].IEEE Transactions on Intelligent Transportation Systems,2015,18(1):25-48.

[2] 李金洋,陈仪香,王振辉.基于车速的自适应交通信号灯控制系统[J].计算机技术与发展,2016,26(9):21-25.

[3] 钱勇生,王春雷.基于三群协同粒子群优化算法的区域交通控制[J].计算机工程与应用,2007,43(14):187-189.

[4] PREETHI P,VARGHESE A,ASHALATHA R.Modelling delay at signalized intersections under heterogeneous traffic conditions[J].Transportation Research Procedia,2016,17:529-538.

[5] ZHANG Yong,WANG Peng.Optimal control for region of the city traffic signal based on selective particle swarm optimization algorithm[C]//International conference on intelligent transportation,big data and smart city.Halong Bay,Vietnam:IEEE,2016:544-550.

[6] ZANG Lilin,ZHU Wenxing.Study on control algorithm of traffic signals at intersections based on optimizing sub-area traffic flows[J].China Journal of Highway & Transport,2012,25(6):136-139.

[7] 陆化普,李瑞敏.城市智能交通系统的发展现状与趋势[J].工程研究:跨学科视野中的工程,2014,6(1):6-19.

[8] 刘脐锺,李 兵.基于改进遗传算法的区域交通信号优化控制[J].西华大学学报:自然科学版,2014,33(6):48-52.

[9] LIANG Chao,FAN Bingquan,HAN Yin.Coordination control method of regional traffic flow[J].Journal of Traffic & Transportation Engineering,2011,50(4):328-332.

[10] XI Jianfeng,LI We,WANG Shengli,et al.An approach to an intersection traffic delay study based on shift-share analysis[J].Information,2015,6(2):246-257.

[11] ZHOU Li,LI Wei.A coordination control by sections on the trunk line of urban traffic network[C]//International conference on multimedia and information technology.Three Gorges,China:IEEE,2009:665-668.

[12] MA Nan,SHAO Chunfu,ZHAO Yi.Study on coordination control with bandwidth optimization for signalized intersections in arterial systems[C]//International conference on optoelectronics and image processing.Haikou,China:IEEE,2011:425-430.

[13] 卢月品,赵 阳,孟跃强,等.基于改进遗传算法的狭窄空间路径规划[J].计算机应用研究,2015,32(2):413-418.

[14] 黄泽霞,俞攸红,黄德才.惯性权自适应调整的量子粒子群优化算法[J].上海交通大学学报,2012,46(2):228-232.

[15] 车海军,刘 畅,孙晓娜,等.基于遗传粒子群算法的冷连轧轧制规程优化设计[J].轧钢,2009,26(1):22-25.