融合项目标签相似性的协同过滤推荐算法

廖天星,王 玲

0 引言

随着数据信息量的增多,为了帮助用户快速找到想要的信息,推荐系统作为处理数据过载问题的有效手段应运而生,并且被广泛地应用在各大个性化网站上,例如亚马逊网站、豆瓣网站等。在电子商务中,个性化的推荐系统已成为当下最强大和最流行的工具之一,并为商业带来了巨大的价值[1]。

在推荐系统中,协同过滤推荐系统作为一种成功的推荐系统被广泛地应用[2]。当前,协同过滤(Collaborative Filtering, CF)推荐算法分为基于记录(memory-based)的协同过滤算法[3]和基于模型(model-based)的协同过滤算法[4],而基于内存的协同过滤又分为基于用户的协同过滤(User-Based Collaborative Filtering, UBCF)和基于项目的协同过滤(Item-Based Collaborative Filtering, IBCF)[5-6]。现在主流的基于用户的协同过滤算法是K-最近邻(K-Nearest Neighbors, KNN)算法,它的基本思想是寻找与目标用户最相近的k个邻居,使用邻居的评分来预测目标用户的评分。基于项目的主流协同过滤算法是Slope One[7],它的基本思想是分析其他项目与目标项目之间的平均评分差异来预测出目标项目的评分。由于这些推荐算法在预测精度上存在提升的空间，本文提出了高精度M2_KSP算法。该算法将KNN用于用户的分类方法变为用于项目的分类方法,将针对Slope One算法忽略项目间关联的问题提出的Slope One加权算法用于设计新的评分预测方法。

M2_KSP算法是一种基于项目的协同过滤推荐算法,该算法的提出首先是通过对KNN算法的研究,发现传统的相似度计算方法如曼哈顿距离、余弦距离等都太过于依赖用户的评分,忽略了项目属性[8]的问题,为解决此问题设计了在算法中融入能够代表项目属性的标签[9]来计算项目间相似度的方法,即M2相似性。然后为了降低评分预测时的计算量,设计使用M2相似性来获得k个邻近项目。最后在参考Slope One加权算法思想下又设计了新的评分预测方法,并基于这k个邻近项目用户的评分预测出目标用户的评分。M2_KSP算法根据KNN算法和Slope One加权算法的理论思想而设计,结合了这两个算法各自的优点,在减少数据计算量的同时又确保了预测评分方法的简单性。

为了验证本文算法的准确度,进行了与基于曼哈顿距离的KNN算法等协同过滤推荐算法的对比实验。实验数据使用了著名的MovieLens数据集,采用Leave-One-Out方法[10]和推荐系统评价指标平均绝对误差(Mean Absolute Error, MAE)和均方根误差(Root Mean Square Error, RMSE)来评价算法的性能。实验结果表明,本文M2_KSP算法具有较高的预测准确度和很好的算法稳定性。

1 相关工作

1.1 基于项目的协同过滤算法

基于项目的协同过滤(IBCF)算法的运算方式一般为:首先使用Leave-One-Out交叉验证方法将数据集划分为训练集和测试集,然后基于训练集数据采用相似性度量方法找到目标项目的相似项目,接着利用相似性作为评分预测算法的权重预测出测试集的评分,最后使用推荐算法评价指标评价算法的质量。这种推荐算法的评分预测都是基于用户评分矩阵的基础之上,可见用户的评分矩阵对推荐算法而言比较重要,故本文将所有项目M={m0,m1,…,m(m-1)}所对应的全部用户U={u0,u1,…,u(n-1)}的评分排列组合成用户项目评分矩阵R,如式(1)所示：

R:U×M

(1)

为使得表示更加明了,这里将矩阵表示为R=(Ri, j)n×m,Ri, j表示用户i对项目j的评分。根据项目的评分规则,有0≤Ri, j≤5,表1是用户评分矩阵的一个示例。

表1 用户评分矩阵示例

表1中,M={m0,m1,m2,m3}表示不同的项目,U={u0,u1,u2}表示不同的用户,Ri, j={2,5,0,3,0,3,2,1,3,4,1,2}。如果Ri, j=0,表示用户i未对项目j评分。

1.2 KNN算法

对于预测目标用户的评分,可以通过KNN协同过滤推荐算法预测该用户对目标项目的评分。由于KNN算法的理念是以用户为中心,寻找用户与用户之间的距离,根据距离的大小来寻找邻近的用户,以邻近的用户都会有相近的评分为原理来预测评分,所以KNN算法的核心是定义用户间相似度。这种方法对用户进行了分类,使用参数k确定用户邻居的数量,通过设置阈值来过滤掉相似度低的用户,其中为了衡量用户间相似度,可以使用欧氏距离和余弦距离[11]计算用户间的距离,距离越近越相似。KNN算法预测评分的计算方法如式(2)所示:

(2)

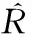
1.3 Slope One加权算法

用于推荐系统的Slope One算法是基于项目之间相互存在的评分差异,不考虑项目之间的相似性直接根据评分的平均差异来预测用户的评分。Slope one算法以其简单性和不错的推荐质量被普遍地应用,当前一部分人针对Slope One算法忽略项目间的内在关联[12]提出了一种改进方法,将项目所占的权重引入Slope One算法中,即为Slope One加权算法[13]。在推荐系统中应用该算法预测目标用户的评分,其计算表达式如式(3)所示:

(3)

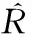
2 本文算法

本文M2_KSP算法是一种基于项目的协同过滤算法,符合一般的基于项目的协同过滤算法通常的运算方式。该算法首先针对例如传统曼哈顿距离计算方法完全依赖用户评分表而忽略项目属性的问题,重新定义了项目相似度计算方法,提出将项目的标签融入计算中；然后为了获得较好的相似度计算效果又提出了通过阈值获得重要标签的方法；最后使用该相似度作为算法的权重来更好地预测出用户的评分。

2.1 项目的标签

针对大多数推荐算法的相似度计算都是基于用户的评分而忽略了项目的属性,本文引入了项目的标签来定义项目相似度。标签可以概括性地描述一个项目,相当于使用离散的语言将项目的特点分离出来。本文使用项目的标签集建立项目标签矩阵。将项目M={m0,m1,…,m(m-1)}和其所拥有的所有标签T={t0,t1,…,t(n-1)}排列组合成该项目标签数量矩阵L,如式(4)所示:

L:T×M

(4)

为使得表示更加明了,这里将矩阵表示为L=(Li, j)n×m,项目j对应标签i的数量表示为Li, j。表2是项目标签矩阵的一个示例。

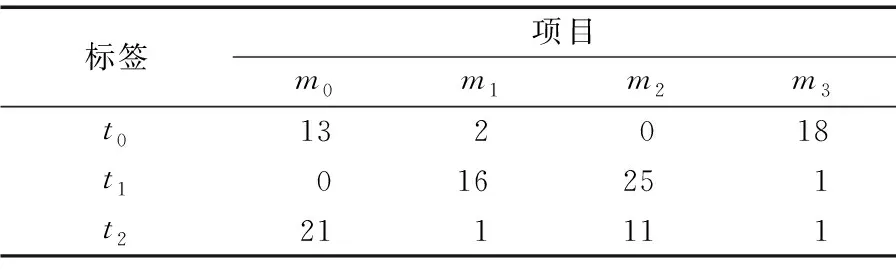
表2 项目标签数量矩阵示例

如表2所示,M={m0,m1,m2,m3}表示不同的项目,T={t0,t1,t2}表示不同的标签,Li, j={13,2,0,18,0,16,25,1,21,1,11,1}。如果Li, j=0,表示项目j不含标签i。

2.2 M2相似性

传统的相似性计算方法强调根据用户的评分相似可以发现用户间相似的偏好,但是由于忽略了项目的属性则不能更好地刻画项目间的相似性,所以本文提出用代表项目属性的标签来定义新的项目间相似性计算方法,即M2相似性。M2相似性依据越相似的项目之间总是具有越多相同的特征属性的理论,这个理论类比于相似的用户间具有更多相同的偏好,这样在理论上可以找到相似的项目。依据理论首先将式(4)中每个标签都看作为物品的一种属性,那么这里的特征属性是指项目具有的重要标签,可以通过设置标签重要度阈值找到重要标签。为了衡量项目中每个标签的重要程度,采用了常用于评估文件中字词重要性的加权技术,即词频-逆文档频率(Term Frequency-Inverse Document Frequency, TF-IDF)方法[14],该方法的计算表达式如式(5)所示:

(5)

其中:Wt为目标项目i中标签t的重要度;Li,t为目标项目i中标签t的数量;Si为目标项目i中所有标签的数量总和;I表示整个项目的数量。

为了量化两个项目间的相似性，本文提出将目标项目所有重要标签与另一个项目的重要标签分别对应相乘累和的方法，计算所得值越大相似度越高，反之则越低。M2相似性具体计算过程为首先通过标签的重要度找到目标项目的重要标签,然后将目标项目与其他项目按照重要标签的数量比例对应相乘,同时并乘上该标签的重要度数值。故本文提出的M2相似性定义方法不同于传统相似性如曼哈顿距离、余弦距离的计算方法,并且有助于下文提及的评分预测算法更快速地预测出目标用户的评分。该相似性的计算公式如式(6)所示:

(6)

其中:Mi, j2为目标项目i和其他项目j之间的相似性;q为重要标签数;Lj,t为其他项目j中标签t的数量;Sj为其他项目j中所有标签的数量总和。

2.3 动态K邻近项目

参考KNN算法用于预测用户评分的思想,此处用来寻找k个邻近的项目,这样做的好处是使用这k个邻近项目用户的评分来预测出目标用户的评分,可以减少评分预测算法的计算量。首先根据式(6)定义的M2相似性方法计算出项目间的相似性,然后使用Rank排序方法对相似度排序即可找到每个项目M={m0,m1,…,m(m-1)}的前k个最邻近项目,在表3中列举了项目m0的两个邻近项目。

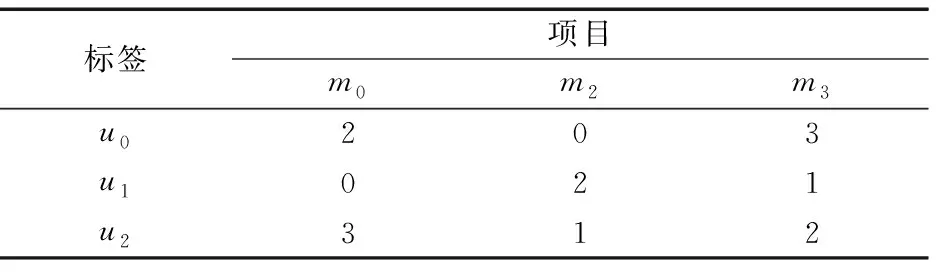
表3 项目 m0 的两个邻近项目示例

如表3所示,k=2,目标项目m0的最邻近两个项目为m2、m3。

2.4 评分预测算法

基于这k个邻近项目的用户评分,使用参考Slope One加权算法设计的新评分预测算法预测用户评分的方法本文称为M2_KSP算法。M2_KSP算法不同于Slope One加权算法,Slope One加权算法采用项目间的加权平均评分差异来预测评分,侧重于计算目标项目与单个项目之间加权平均评分的差异；而本文M2_KSP算法则侧重于计算目标项目与所有邻近项目整体的加权平均评分的差异。本文算法的计算过程为：首先计算目标项目平均评分,然后计算出与邻近项目整体加权平均评分的差值,最后将这个差值加到目标用户的平均评分上,由此预测出目标用户的评分。M2_KSP算法的时间复杂度为O(n+m)，相对于Slope One加权算法以及KNN算法的时间复杂度更低,其评分预测方法的表达式如式(7)所示:

(7)

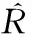
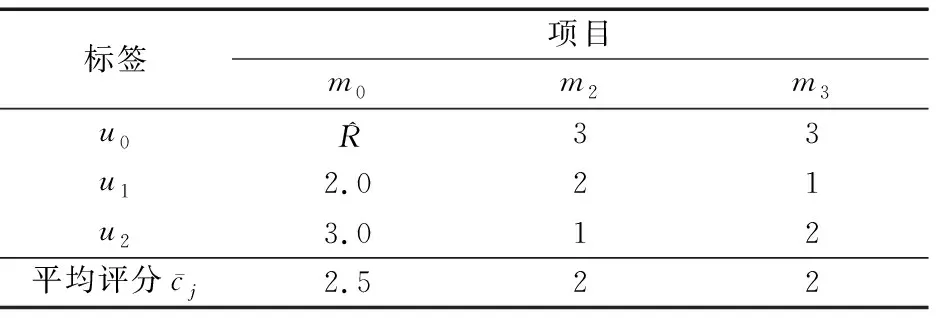
表4 目标项目 m0 的评分矩阵

本文所提出的融合项目标签相似性的协同过滤推荐算法(M2_KSP)的运算步骤如下所示：

输入 标签矩阵L和评分矩阵R,邻近项目数k,目标用户i,目标项目j。

1) 根据式(6)生成项目间的相似性矩阵F;

2) 根据F矩阵形成k个邻近项目评分矩阵;

3) 初始化csum=0;c=0;sum=0;s=0;bsum=0;b=0;

4) fora=0 ton-1

5)csum+=ra, j;c++;

6)

7) end fora

8) forf=0 tom-1

9)sum+=ri, f;s++;

10)

11) end forf

12) forb=0 tok-1

13) if(ri,b<1E-6)

14) continue;

15) end if

16)

17) end forb

18)

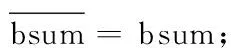
19)

3 实验与分析

3.1 实验的数据

本文选择的是GroupLens Research小组所收集的最新的带标签的MovieLens数据集(http://grouplens.org/datasets/movielens/),该数据集含有24 404 096个评分,668 953个标签和40 110部电影。在本次实验中,随机从该数据集中选取了前1 000部电影和与之对应相关的11 102个用户,7 951个标签作为实验的数据来进行实验。本次实验数据集的稀疏度为97.65%,实验数据的用户评分比例如图1所示。

图1 用户评分比例

3.2 推荐算法评价指标

平均绝对误差(Mean Absolute Error, MAE)是评价推荐算法质量的标准之一,作为推荐系统的评价指标被广泛地应用于算法质量的评价[16]。本文使用MAE作为推荐算法准确性的度量,在实验结果中MAE的值越小表示该算法的平均绝对误差越小,即该算法的准确度越好。MAE的计算公式如式(8)所示:

(8)

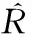
推荐算法的另一个评价指标是均方根误差(Root Mean Square Error, RMSE)[17]。本文为更准确地衡量该算法的预测效果,也使用了RMSE评价方法来衡量预测值与真实值之间的偏差。RMSE的计算公式如式(9)所示:

(9)

3.3 实验结果与分析

在实验过程中,首先使用Leave-One-Out交叉验证方法将实验的数据划分为训练集和测试集。为了找到最优的标签重要度阈值a,进行了阈值a在不同取值时对算法的准确度所造成影响的实验,实验结果如图2所示。接着通过设置最优阈值a获得项目的重要标签并且使用重要标签的数量计算项目间相似度。然后,对相似度进行rank排序获得目标项目的k个邻近项目。最后,基于这k个邻近项目的评分,使用新定义计算目标项目与整个邻近项目的平均评分差异的方法预测用户的评分。同时,为了比较该算法的预测性能,在相同的数据集上将本文提出的M2_KSP算法与其他推荐算法进行实验。

对比算法包括：基于曼哈顿距离的KNN算法(称为M_KNN)、使用M2相似性作为权重的Slope One加权算法(称为M2_Slope One算法)，以及本文M2_KSP算法。M_KNN算法是使用曼哈顿距离计算相似度的KNN协同过滤推荐算法,M2_Slope One是一种使用M2相似性的Slope One加权协同过滤推荐算法,这些算法都是比较流行的协同过滤推荐算法。

在M2_KSP算法中通过设置阈值a来找到项目的重要标签，具体方法为判断项目的标签重要度是否大于a,若是则表明该标签为重要标签。阈值选取越合理越能获得真正重要的标签。本文为了设置最佳阈值a进行了相关实验,结果如图2所示a的取值为每个标签的权重在项目标签权重总值中所占的比例,随着k值的变化在a的取值从大到小的过程中,所取得的算法的平均绝对误差值形成折线变化趋势，且每条折线间的距离越来越靠近,当a的取值分别为0.001、0.000 5、0.000 3时这三条折线几乎完全重合，可学习到该算法最佳的阈值范围为0.000 3～0.001,算法的阈值设置在这个范围内更加合理，故本文算法的最优阈值a取值为0.000 5。

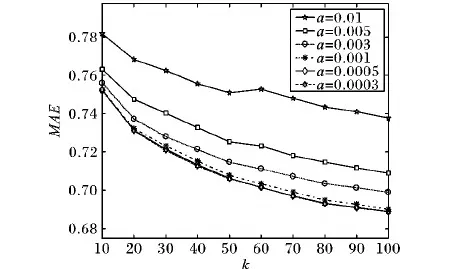
图2 在阈值a影响下算法的平均绝对误差

算法MAERMSEM_KNN0.7640.974M2_SlopeOne0.7270.952M2_KSP0.6880.903

由图3和表5可知，在MAE评价标准下,随着k的不同取值,本文提出的基于a的最优阈值M2_KSP算法取得的最小误差明显比M_KNN算法的最小误差值小很多,即M2_KSP算法的准确度明显高于M_KNN算法,同理也略高于M2_Slope One算法。通过图3的实验结果表明,M2_KSP算法是一种预测准确度较好的协同过滤推荐算法。

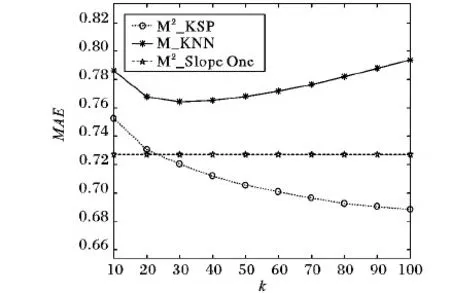
图3 不同算法的平均绝对误差对比(k取10～100)

由图4和表5可知：本文M2_KSP算法在RMSE评价标准中相对于M_KNN算法同样具有一个相对较低的误差值，并且在k取值大于30时，M2_KSP算法的误差值低于M2_Slope One算法,由此再次验证了M2_KSP算法预测精度好于M_KNN算法,同时也略优于M2_Slope One算法。再结合图3的实验结果综合得出,本文提出的M2_KSP协同过滤算法的推荐准确度是更加精准的,推荐的质量也是更加优秀的。

图4 不同算法的均方根误差对比

为了观测M2_KSP算法的稳定性,进行了加大k取值范围的实验，实验结果如图5所示。

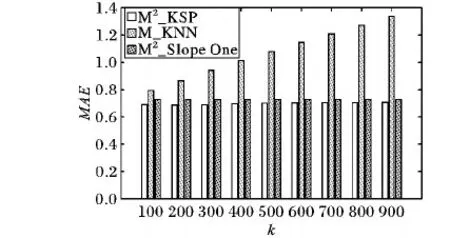
图5 不同算法的平均绝对误差对比(k取100～900)

从图5中三种算法的误差对比分析可知：在相同数据集下M2_KSP算法在不同的k值下的平均绝对误差值的变化最小，并且稳定在最小的误差值范围内；但是M2Slope One算法取得的MAE值变化幅度则更大、稳定性更差；M_KNN算法取得的MAE值变化幅度最大且波动在最大的误差值范围内、稳定性最差。所以本文提出的M2_KSP算法相比而言具有更好的稳定性。综上所述,M2_KSP算法无论是在MAE评价标准下还是在RMSE评价标准下都表现出更精确的预测评分准确度、更好的推荐质量、更优秀的算法稳定性,故本文提出的M2_KSP算法是一种可行有效的、具有更高准确性和更好稳定性的协同过滤推荐算法。

4 结语

本文参考KNN算法的思想，首先依据重要标签数量定义了项目间M2相似性,该相似性旨在寻找目标项目最邻近的k个项目。然后基于这k个邻近项目用户的评分,并通过对Slope One加权算法的研究设计了M2_KSP评分预测算法。本文算法依据KNN算法思想和Slope One加权算法理论设计而成,故具有一定的理论依据,同时也结合了这两个推荐算法各自的优点,在减少算法计算量的同时又保证了算法的简单性。实验结果表明，本文算法表现出了更好的准确性,符合预期的猜想，并且还具有很好的稳定性。总而言之,本文算法具有更精确的准确度、更优秀的推荐质量和良好的稳定性。从图3～4中可知随着k值变大,算法的误差率逐渐降低，即评分数据量越多算法的预测准确度越高,而目前用户评分矩阵比较稀疏,计划未来在减小评分矩阵的稀疏度上能提出好的方案。

由于本文算法是采用Leave-One-Out交叉验证方法,该方法在数据的样本数量较大时需要消耗的时间较多,未来为了更好地实现实时的推荐可以考虑采用并行化计算方法来减少计算所需的时间。

参考文献(References)

[1] RICCI F, ROKACH L, SHAPIRA B. Recommender systems: introduction and challenges[M]// RICCI F, ROKACH L, SHAPIRA B. Recommender Systems Handbook. Berlin: Springer, 2015: 1-34.

[2] BOBADILLA J, ORTEGA F, HERNANDO A, et al. Recommender systems survey[J]. Knowledge-Based Systems, 2013, 46: 109-132.

[3] JEONG B, LEE J, CHO H. Improving memory-based collaborative filtering via similarity updating and prediction modulation[J]. Information Sciences, 2010, 180(5): 602-612.

[4] ZHANG H R, MIN F, WANG S S. A random forest approach to model-based recommendation[J]. Journal of Information and Computational Science, 2014, 11(15): 5341-5348.

[5] LÜ L, MEDO M, CHI H Y, et al. Recommender systems[J]. Physics Reports, 2012, 519(1): 1-49.

[6] PIRASTEH P, JUNG J J, HWANG D. Item-based collaborative filtering with attribute correlation: a case study on movie recommendation[C]// ACIIDS 2014: Proceedings of the 6th Asian Conference on Intelligent Information and Database Systems. Berlin: Springer, 2014: 245-252.

[7] BASU A, VAIDYA J, KIKUCHI H. Perturbation based privacy preserving slope one predictors for collaborative filtering[C]// IFIPTM 2012: Proceedings of the 6th IFIP WG 11.11 International Conference on Trust Management VI. Berlin: Springer, 2017, 374: 17-35.

[8] KIM H N, JI A T, HA I, et al. Collaborative filtering based on collaborative tagging for enhancing the quality of recommendation[J]. Electronic Commerce Research and Applications, 2010, 9(1): 73-83.

[9] PITSILIS G, WANG W. Harnessing the power of social bookmarking for improving tag-based recommendations [J]. Computers in Human Behavior, 2015, 50: 239-251.

[10] CAWLEY G C. Leave-one-out cross-validation based model selection criteria for weighted LS-SVMs[C]// IJCNN 2006: Proceedings of the 2006 International Joint Conference on Neural Networks. Piscataway, NJ: IEEE, 2006: 1661-1668.

[11] ZHENG M, MIN F, ZHANG H R, et al. Fast recommendations with the M-distance[J]. IEEE Access, 2016, 4: 1464-1468.

[12] 李淋淋,倪建成,于苹苹, 等. 基于聚类和Spark框架的加权Slope One算法[J]. 计算机应用, 2017, 37(5): 1287-1291, 1310.(LI L L, NI J C, YU P P, et al. Weighted Slope One algorithm based on clustering and Spark framework[J]. Journal of Computer Applications, 2017, 37(5): 1287-1291, 1310.)

[13] TIAN S, OU L. An improved slope one algorithm combining KNN method weighted by user similarity[C]// WAIM 2016: Proceedings of the 2016 International Conference on Web-Age Information Management. Berlin: Springer, 2016: 88-98.

[14] 李镇君, 周竹荣. 基于Document Triage的TF-IDF算法的改进[J]. 计算机应用, 2015, 35(12): 3506-3510, 3514.(LI Z J, ZHOU Z R. Improvement of term frequency-inverse document frequency algorithm based on Document Triage[J]. Journal of Computer Applications, 2015, 35(12): 3506-3510, 3514.)

[15] ANIDORIFON L, SANTOSGAGO J, CAEIRORODRIGUEZ M, et al. Recommender systems[J]. Communications of the ACM, 2015, 40(3): 56-58.

[16] CREMONESI P, GARZOTTO F, NEGRO S, et al. Looking for “Good” recommendations: a comparative evaluation of recommender systems[C]// INTERACT 2011: Proceedings of the 13th IFIP TC 13 International Conference on Human-Computer Interaction, LNCS 6948. Berlin: Springer, 2017: 152-168.

This work is partially supported by the National Natural Science Foundation of China (41674141).