无模型自适应控制算法在控压钻井自动控制系统中的应用

丁慧

摘要：控压钻井自动控制系统主要通过改变井口回压的手段来维持井底压力的恒定。进行数学建模时受控压钻井工区结构、井口装置等各方面因素影响，很难建立精确的数学模型。本文分析了基本控制原理之后，提出无模型自适应控制（ MFAC）算法，不依赖于控制系统的数学模型，只需要系统的输出可观输入可控。给出了详细的MFAC控制率求解方法以及伪偏导数预估方法，结合近似滞后二阶惯性环节，进行了仿真研究。从仿真结果可看出MFAC控制算法能满足控制要求，达到控制目的。

关键词：控压钻井；伪偏导数；无模型自适应控制

控压钻井的主要任务是能够对井底的压力精准控制，保证井底的压力在安全密度窗口之内。在钻井过程中影响井底压力的因素有静液柱压力、环空压力损耗以及井口回压三个因素，其中静液柱压力与钻井液的密度有直接的关系[1]，一般不能快速被调整，而环空压力的损耗受多种因素的影响，比如钻井泵的排量、井身结构，钻具的转速等多个因素，可控性比较小。那么对于自动控制系统而言，只能去改变井口回压来补偿压力的损耗，以维持井底压力恒定。

井口回压是靠地面节流管汇系统的节流阀和平板阀的开度来进行调节的，这就要求控压钻井的自动控制系统需要在大量实践基础上建立的一整套专家系统和智能化控制算法以满足智能化控压钻井的特定测控要求。

1 控制系统结构

控制系统主要完成两大任务： （一）实时在线检测井口人口流量、人口压力、回压泵入口流量、回压泵压力、井口回压、节流阀后压力等工艺参数。 （二）根据入口流量、人口压力及控压钻井工艺参数要求对节流阀的开度和平板阀的开关动作实现自动控制。

自动控制系统主要完成对流量、压力、阀状态等现场数据的采集，对节流阀的开度和平板阀的开关，以及泵的启/停自动控制，并完成上傳所采集的现场数据，及接收管理级计算机的生产指令等功能。白动控制系统由控制器、信号隔离器、驱动泵启停逻辑、保护电路等组成。

2 控制原理

控压钻井的核心问题在于对井口压力的控制[2]。整个控压钻井的施工流程在不同的工区可能不尽相同，但是总体来说有四个基本程序：开泵、正常钻井循环、停泵、停止循环。对于控制而言，最关键的控制点在开泵和停泵两个时刻，当开泵的时候，井口压力要能够迅速降低，停泵的时候，井口压力能够迅速得到升高，以补偿环空压力损耗，维持井底压力恒定。

2 1 基本控制原理

控制系统的控制原理为通过控压钻井装备与工艺的有效结合，依据采集的排量、套压、立管压力等工艺参数，通过录井设备获取的钻进深度、钻井泵冲、泥浆排量、钻井液密度等井场信息数据，进行精确的水力计算和合理的逻辑判断，实时对比实际井口压力与目标压力，依据二者的偏差，通过控制系统发出控制节流撬中节流阀的信号，调节节流阀的开度以改变井口回压，实现控制井底压力的目标。可分为恒压控制和微流量控制。

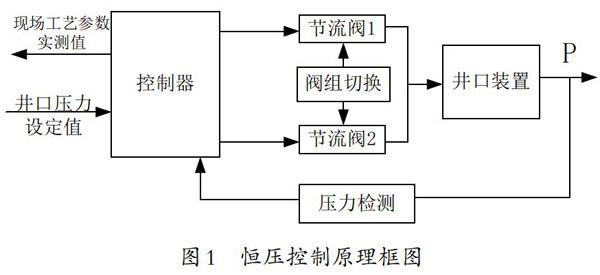
恒压控制原理如图1所示：

恒压控制是在钻井作业过程中保持近钻头井底压力恒定（井底恒压模式）或保持泥浆出口压力恒定。其控制手段是通过调节节流管汇上节流阀开度，实现控制井口压力来间接达到井底压力控制的目标。当停止循环时，也采用恒压控制，通过回压泵系统来对井口的压力进行补偿，控制原理和正常循环钻进时类似，只是控制手段是调节回压泵系统的节流阀开度实现压力的调节。恒压控制框图如图2所示。

微流量控制原理如图3所示：

控制器具体实现对井口微流量恒定的控制：一方面接收上位机HMI软件下传的井口流量设定值（ Qr），同时经井口流量计实时在线检测井口实际流量（ Qf），根据设定流量与实际流量的偏差（△Q）自动调节节流阀开度，以实现对井口流量的控制使实际井口流量与设定流量保持一致，达到井口微流量控制的目的。微流量控制框图如图4所示。

通过以上分析，常规的控制算法均需要精确确定数学模型。在控制领域有许多先进的控制算法，但是大多数的控制算法都依赖于精确的数学模型，对于复杂的控制系统，很难建立数学模型。在控压钻井施工工区，地质结构本身具有太多的不确定性，地层也是不均匀特性，钻井施工过程中也存在很大的随机性，所以很难建立起系统的数学模型，对于有的施工现场甚至不能建立模型，精确的预测数学模型难以满足控压钻井的控制需求。因此，在控压钻井自动控制系统中我们提出无模型白适应控制（ MFAC）算法。这种算法不依赖于系统的数学模型，而且具有很强的鲁棒性和适应性。

2.2 MFAC控制理论

MFAC控制算法本身在理论上就具有闭环系统的稳定性分析和判据，能够保证控制系统的稳定性，在算法实现过程中不需要对过程进行系统辨识，不需要进行精确的定量，也不需要较为复杂的人T工控制器相关参数的整定，这些特征非常适合控压钻井控制系统特点。

离散的非线性系统一般表达式为：

y（k+1）=f（y（k），……y（k-m），

n（k），……u（k-n）

（1）

从（1）式可以看出系统输入输出的关系以及阶次，处理这样的非线性系统一般是通过各种合适的算法将非线性系统转换为易处理的线性系统。在MFAC理论方法中，采用的是泛模型方法。简单点说就是将非线性系统进行动态线性化，推导得到带有时变因子的线性系统模型。

首先假设系统的输入是可控的，而且输出是可观的，也就是说保证系统的输出一定是由相关的可以控制的输入信号引起，且能达到控制目标。其次也要假设系统输入连续变换时输出也能连续变化。同时（1）式也要满足广义谱希茨条件，即

在任意时刻k和，有Au（k）≠0

|△y（k+1）|≤b|△u（k）| （b>0）

其中△y（k+ 1）=y（k+ 1） - y（k）

△u（k）=u（k） - u（k-1）

当△u（k）≠O，则一定存在一个伪偏导数Ф（k），使得

y（k+1）- y（k）=Ф（k）（u（k） -u（k-1）） （2）

可以理解Ф（Jt）为y（k十1）关于u（k）的梯度，且≤b。这一点就体现了系统的白适应特点，也是MFAC理论中的泛模型。给定系统输出设定值y（k+1），通过控制器输出u（k），作用于执行机构，达到系统输出、（k+1）=y+（k+1）的目的。这里，Ф（k）是未知的，但是可以根据观测的数据{u（k -1）.y（k）}，可以得到Ф（k -1）的预估值Ф-（k -I），从而推导得出c0（k）的预估值Ф（k）。

系统线性化表达式变为：

（一）控制率的求解

泛模型的引入，使得非线性系统动态近似线性化，这时需要对系统输入信号的变化量进行限制。对于非线性系统而言，如果输入信号的变化量过大，也就是说系统输入发生突变，很容易造成系统不稳定。因此，控制器的控制算法必须要同时考虑系统稳态偏差和系统稳定性。对于一般离散系统，大多采用最小化相邻步数的系统输入误差为目标来进行控制。因此，输入目标控制函数用（4）式来表示。

控制過程基本上是这样一个过程：在t时刻，依据t-1时刻的输入输出数据预估伪偏导数Ф（k），然后将Ф（k）代人（6）式，使反馈回路检测的信号尽量跟随控制器设定的输出，然后反馈到系统输入端，使新的观测值作为控制器的输入信号，依据这个输入的新数据，对Ф（k.1）进行计算，以此往复，最终使系统稳定而且稳态误差最小。

这样一个控制过程基本就是（6）式和（8）式交替计算达到控制的目的。控制原理框图如图5所示，MFAC控制结构框图如图5所示。

在MFAC控制率中，涉及到两个因子，一个是学习步长γ和λ。若Ф（k）≤ε（ε>o）或|△u（k -1）l≤τ，ε是无穷小的正数，则Ф（k）=Ф（1）。

3 MFAC仿真研究

在MATLAB simulink中没有MFAC模块[3]，在对控压钻井自动控制系统进行仿真前需要封装MFAC模块，然后借助simulink中的相关模块进行仿真。

封装后的模块如图7所示

Reference是参考输入，scope是matlah中的示波器模块。从图示可以看出控制器独立于系统模型。

系统被控对象为调节阀及其伺服机构井口装置，流量检测等。由于流量调节响应速度较慢，可视为有滞后二阶惯性环节，即对系统子模型表达式为

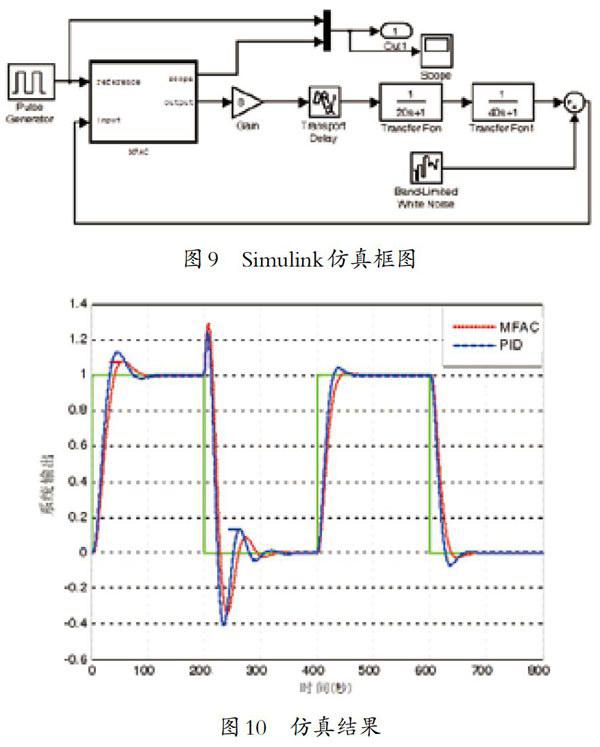
为了验证MFAC算法的有效性，针对有滞后二阶惯性环节，采用PID控制算法做对比，系统数学模型近似如图8：

从图中可以看出，PID控制算法也能达到控制目的，但是MFAC算法的超调量稍小，在仿真过程中加入一定的噪声，白噪声是方差为0.01的信号，可以看出MFAC算法具有一定的白适应性，响应的速度也有一定的优势。

4 结论

在立压、套压、流量三个工作流程中均存在非线性因子，且非线性程度随运行工况也会发生变化，采用无模型白适应算法忽略系统数学建模的问题，同时也可以解决动态非线性的控制问题。在施工过程中可以实现手自动投运、多目标转换、设定值跟踪等动作，以达到对液动节流阀的调节平滑无扰。经过实验室试验，控制系统能实现井底压力控制和微流量控制，全工况回压控制精度达到0.5MPa。

参考文献：

[1]蒋宏伟，周英超等控压钻井关键技术研究[J]石油矿场机械，2012，41（1）：15

[2]周英操，杨雄文等PCDS-1精细控压钻井系统研制与现场试验[J]石油钻探技术2011，39（4）： 7-12

[3]李传庆，刘广生基于Matlab-Simulink的MFA控制模块开发与仿真[J]控制工程，2008，15（s1）：61-62