基于FPGA的BP神经网络硬件实现及改进
2018-06-19杨景明杜韦江吴绍坤魏立新
杨景明,杜韦江,吴绍坤,李 良,魏立新
(1.燕山大学 工业计算机控制河北省重点实验室,河北 秦皇岛 066004;2.国家冷轧板带装备及工艺工程技术研究中心,河北 秦皇岛 066004)
0 引 言
软件串行实现BP神经网络一直存在网络收敛速度过慢、实时性差的问题,而可编程逻辑器件FPGA的出现给神经网络提供了一种有效的硬件实现方式。FPGA可通过并行计算的方式,在一个周期内完成多个运算,且其可编程以及可重构能力大大缩短了神经网络的设计周期,这使得利用硬件实现大型神经网络成为可能[1-3]。很多文献也对这一课题进行了深入研究,但仍有一些不足之处,文献[4]运用脉动门阵列的方法实现了BP神经网络,但是大大降低了网络的并行性;文献[5]成功的运用查表法实现了BP神经网络的sigmoid函数,但将更新权值存储在RAM中的方式使得运算不够灵活;文献[6]成功利用1-3-1网络对cosx函数进行了逼近,但没有对相对复杂的函数进行进一步的验证。
基于这一现状,本文对激活函数实现、资源合理分配、以及存储方式选择等关键性问题进行了研究,并提出了寄存器循环缓存方式以及串并联相结合的计算方法,对FPGA实现BP神经网络进行了改进,有效节省了资源,提高了BP神经网络的训练速度。
最后利用简单函数以及复杂函数对网络进行了大量的实验,并与软件实现进行了对比,验证了基于FPGA神经网络的实时性以及高效性。
1 关键问题设计方案
1.1 双极性S函数的硬件实现
对于在FPGA中实现神经网络,激活函数的选取和实现是关键问题之一。由于双极性S函数既具有非常好的线性区域又具有非常好的非线性区域,使其能够同时对小信号和大信号进行处理,对于存在负相关系的复杂函数其要比单极性S函数作为激活函数有一定的优势。因此,本文选择双极性S函数作为神经网络隐含层的激活函数,而输出层则选择对称饱和线性函数作为激活函数。
非线性函数不能够在FPGA中直接实现,只能通过某些方法对其进行逼近,对于硬件实现激活函数,需要充分考虑多方面的因素,这就意味着逼近效果最好的方式并不一定适合于硬件实现。本文通过综合考虑FPGA资源与精度,选择分段函数与查表法相结合的平滑插值法对双曲正切函数进行逼近。这种函数逼近法实质上就是通过一系列的线性函数来对激励函数进行拟合,然后所得系数利用查表的方式表示出来。将激励函数分为不同的区间,并运用最小二乘法对多项式进行拟合,最终用多个线性函数将双曲正切函数表示出来。因为双曲正切函数的正区间与负区间关于原点对称,所以为了节省资源,在取负值时,通过取绝对值带入正值区域再取反的形式获得,这种方式有效的节约了对FPGA资源的利用。图1为分段函数在[0,1]、[1, 2]、[2, 3]、[3, 4]对双曲正切函数进行分段逼近情况。
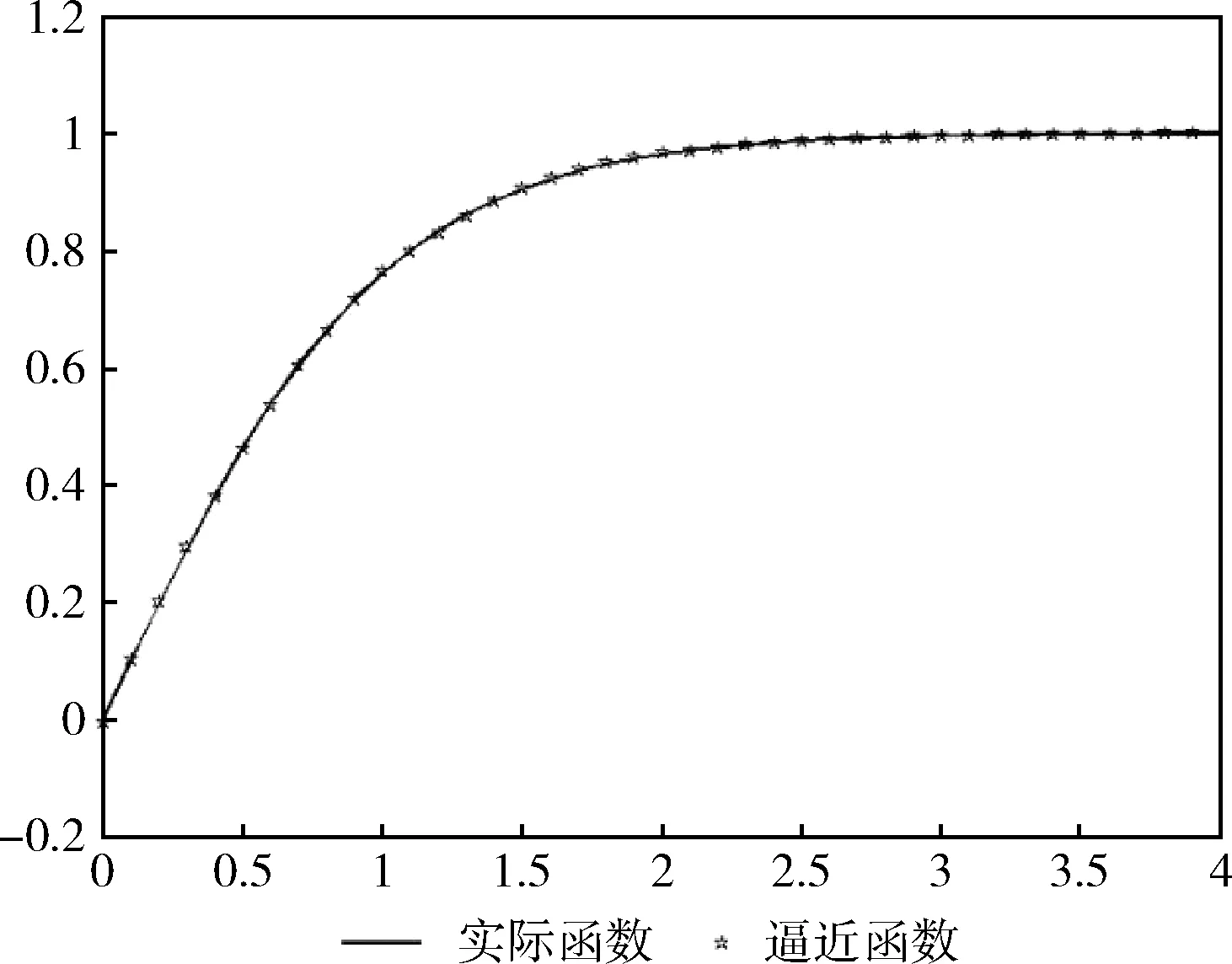
图1 函数分段函数逼近情况
根据逼近情况可将双曲正切函数分为5段,逼近函数与其绝对误差见表1,可以看出,逼近函数的输出值与双曲正切函数的理论值误差小于0.01,说明利用平滑插值法逼近在FPGA中实现激活函数完全可行。该模块用quartus ii进行编译之后,生成的双极性S函数的电路原理如图2所示,所占ALMS为220,不足实验平台FPGA芯片的1%;与利用polyfit实现单极性S函数相比,节省了更多的硬件资源[7],与分15段实现了S函数相比,不仅实现起来更加简便,且精度更高[4]。相比之下该方法使函数的精度、性能与成本达到了一个更加良好的平衡。

表1 双曲正切函数各区间逼近函数及误差
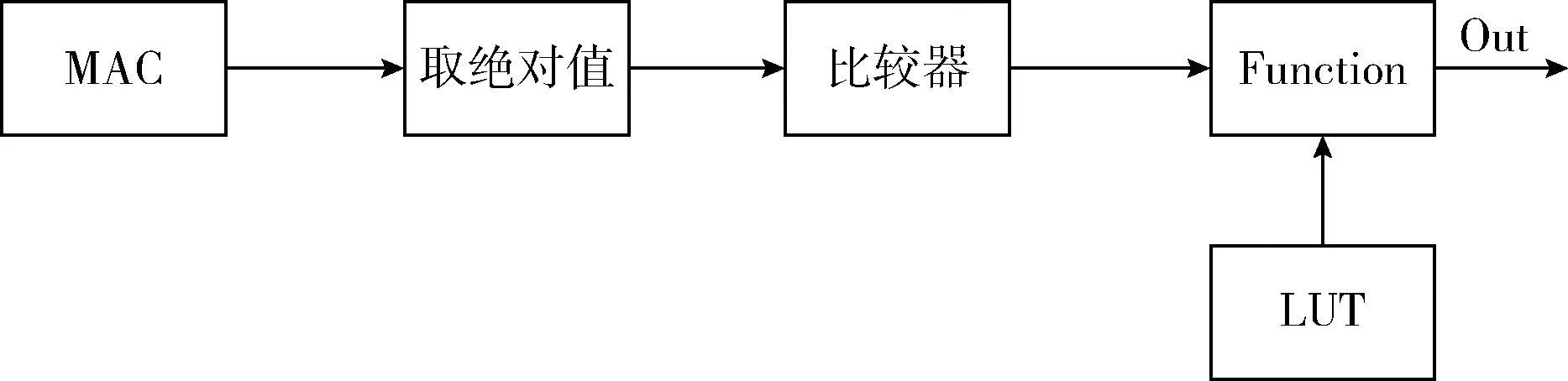
图2 双极性S函数电路原理
1.2 循环缓存技术的应用
如何通过合理的存储方式来获取和传输数据也是需要考虑的问题之一。大多数参考文献均采用分布式RAM存储激活函数的常数,而将权值及样本数据存储在 SRAM 或DRAM 等外部存储器中,但由于片外存储设备的带宽限制,数据很难达到并行输入输出,使其不能直接满足计算的需求[8]。因此本文使用了一种寄存器循环缓存的方法来进行权值的存储,不仅给数据的输入输出提供了足够大的位宽,而且使其在单时钟内可以并行的输入输出。
如图3所示,神经网络初始权值由外部存储设备给定,每次训练后的数据既不存储到外部存储中去,也不存储在FPGA片上固有的RAM中,而是直接缓存到寄存器中进行下一轮的学习,训练全部结束或者遇到突发情况时才会将权值存储到外部掉电可保存的设备中。图4为通过quartus ii的逻辑编译后所产生的部分逻辑单元,其中V11、V12、V13、V14为神经网络更新后权值,其值将锁存到寄存器中,并在下一次误差运算之后发送出V_11、V_12、V_13、V_14作为待更新权值,然后与权值增量进行运算生成新的权值。得到的新权值不仅用于接下来乘累加运算,还要存储在缓存寄存器中等待下一次的权值更新。这种存储方式与FPGA的流水线方式相结合,可以大大减少对外部存储的重复访问,降低了存储带宽的耗费,提高了对片外资源的利用率。且与将权值存储在片上RAM相比,不但简化了整体网络设计的复杂度,还使片上的存储资源得到了合理的分配。
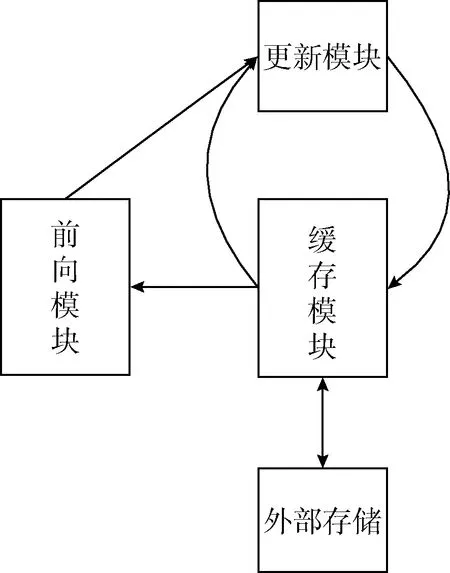
图3 寄存器循环缓存结构原理
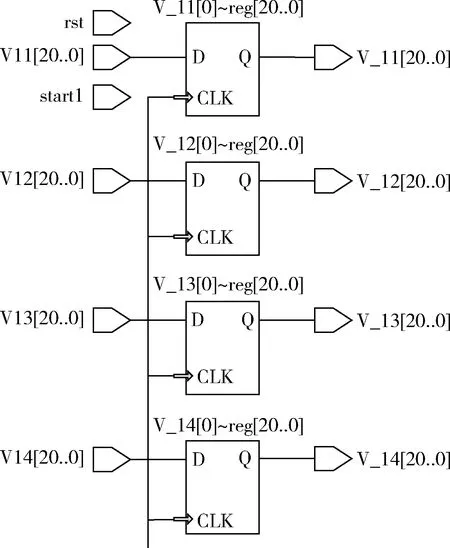
图4 寄存器循环缓存结构逻辑
1.3 并行计算与深度流水线技术
采用FPGA实现神经网络是因为其良好的并行性与神经网络的运算方式相符。但正是因为大多数设计与实现过分倾向于实现对神经网络的高度并行,而忽略了阿穆达定律的含义,该定律指出最终的加速受到串行或者低速并行处理的限制。在一般情况下,神经网络的结构形式在硬件中实现完全并行是不可能的,必然存在着一些顺序处理,所以必须选择最适合硬件的并行结构来完成神经网络结构在FPGA中的最佳映射。本文采用并行与串行结构相结合的方式进行了BP神经网络在FPGA中的实现,各层神经元之间采用并行运算,而模块之间采用FPGA的流水线技术。
神经网络的层与层之间采用FPGA的流水线的设计方法,主要是将原本一个时钟周期完成的较大组合逻辑通过合理的切割后分由多个时钟周期完成,这样一来该部分运行的时钟频率将会有明显提高。如图5所示,采用这种设计,虽然第一次输出有较大的延迟,但若干个周期后,每个时钟周期都能进行一次输出,大大提高了数据处理的频率。流水线技术的应用,需要各模块之间时序上能够进行合理的分配,通过各种使能信号设定,使BP神经网络在FPGA中实现多级流水线结构。
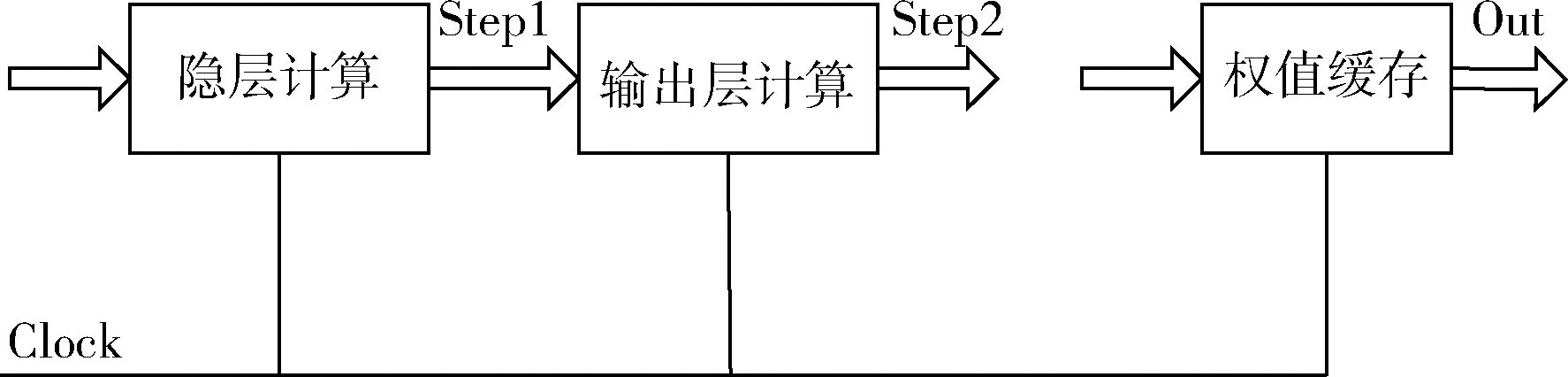
图5 流水线实现结构
在具体设计过程中,程序设计采用了顶层模块式结构,共分为隐层模块、输出模块、误差计算模块、误差更新模块以及权值缓存模块等5部分,而各模块内部又可分为若干个子模块,例如隐层模块可分为输入模块、乘累加模块、激活函数模块,各部分内部均并行计算,模块之间通过添加使能信号的方式实现流水线设计。如图6所示,start0~start6使能信号分别控制着各模块的运行,e为输出层误差,w_r1为隐层权值增量。可以看出,start1控制整个前向通道,start3为误差计算模块的使能信号,当经过一个时钟周期后,输出层误差e发生变化,而start4为权值更新层的使能信号,当经过一个时钟周期后,隐层权值增量w_r1发生变化。使能信号的设置是FPGA进行复杂电路设计时必不可少的环节之一,在同一时钟下,通过寄存器边沿触发的方式产生使能信号,并将其传输到下一个处理的模块中去,可以有效的避免模块过多所产生的时序冲突,便于程序的时序约束及时序仿真。
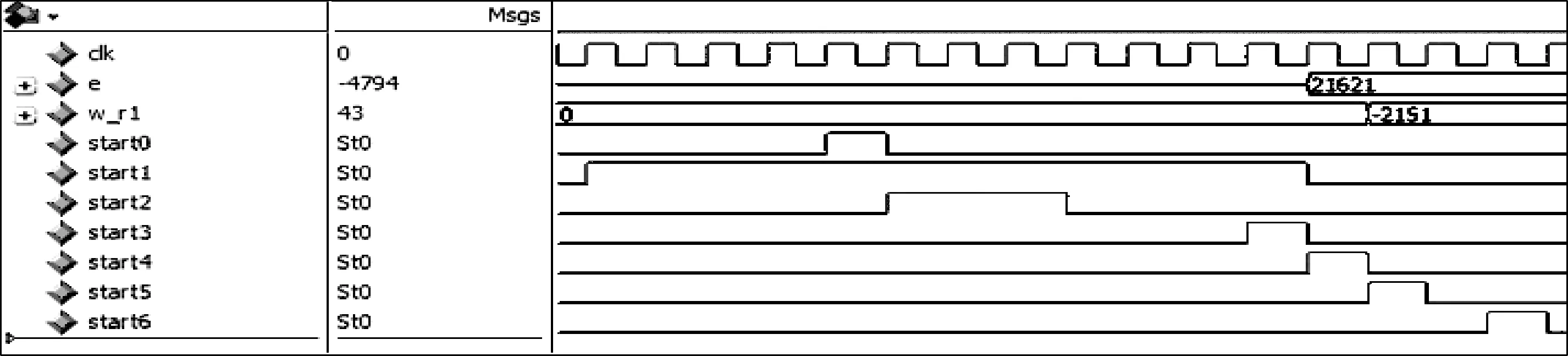
图6 使能信号的设置
正是因为FPGA独特的流水线设计,使其在延时方面比GPU实现神经网络有着核心的优势,尽管GPU与FPGA一样都能够进行并行运算,但流水线深度受限的GPU因为数据延时高达毫秒级,而运用FPGA的深度流水线技术与并行相结合的方式可将延时控制在纳秒级,对于流式计算任务,FPGA天生有延时方面的优势。
2 实验与仿真
本文选用DE1-SOC实验平台进行实验验证,该平台选用Altera公司的CycloneV系列的5CSEMA5F31C6N芯片,并与PC平台进行了实际计算效率对比。实验所用芯片最大工作频率为800MHz,ALMs为32070,且具有475个可使用的I/O接口,实验所用PC配置为Intel(R)core(TM)i5-6500 CPU 3.20 GHz,内存为8G。分别在FPGA芯片与PC中运行相同的BP神经网络结构,并进行对比。
程序使用21位定点小数进行实现,其中1位符号位,8位整数位,12位小数位,数据以-4096~+4096进行归一化运算,运算结束后再将其反归一化。本文通过实验对数据精度进行了验证,该表示方法可以完全满足BP神经网络的收敛运算。
2.1 单输入BP神经网络逼近sinx函数
参考文献中出现很多运用BP神经网络逼近sinx函数,本文也利用了1-6-1的BP神经网络对sinx进行了逼近实验。首先选择31个数据,进行归一化后先在PC中运用相同结构的神经网络进行训练,在误差小于0.01时,程序完成收敛过程并结束。同时将样本在[-4096,4096]区间内进行归一化,隐层、输出层权值为在PC训练中随机产生的初始权值,然后在Modlsim软件中对FPGA实现的神经网络进行训练仿真,也同样在误差小于0.01时完成训练,经过20次实验后,将PC中的训练结果与FPGA进行对比,见表2,数据为多次训练后的平均值。
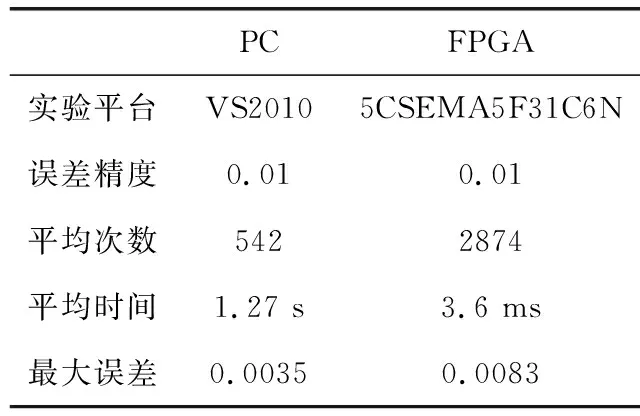
表2 PC与FPGA实现sinx比较
可以看出,对于简单的函数,FPGA的训练的速度要快于PC,但由于训练时间都很短,所以利用FPGA实现神经网络看不出明显的优势。
2.2 多输入BP神经网络逼近复杂非线性函数
T=T13+T12-2.5*T1
(1)
其中,T1=sin(2*pi*x1)+ex2。
为了验证FPGA硬件实现神经网络在速度方面的优势。文章利用2-12-1神经网络逼近函数式(1)的T函数,选取70个归一化后的训练样本进行训练,首先运用PC实现同样拓扑结构的BP的神经网络,初始权重随机给出,当误差小于0.01时训练结束,图7为PC中训练的函数逼近情况,然后利用PC中同样的随机权值,在FPGA中进行训练,同样误差小于0.01时训练结束,训练结果如图8所示,其中x1为一项输入,y0为期望输出,y为实际输出,由图可知,本次训练在178 ms时完成对期望函数的逼近。FPGA资源消耗情况见表3,因为程序中运用了大量的乘累加运算,所以占用了所有的DSPS;训练结束后,选取测试值对训练好的网络进行测试,测试结果见表4、表5,精度皆符合逼近要求。
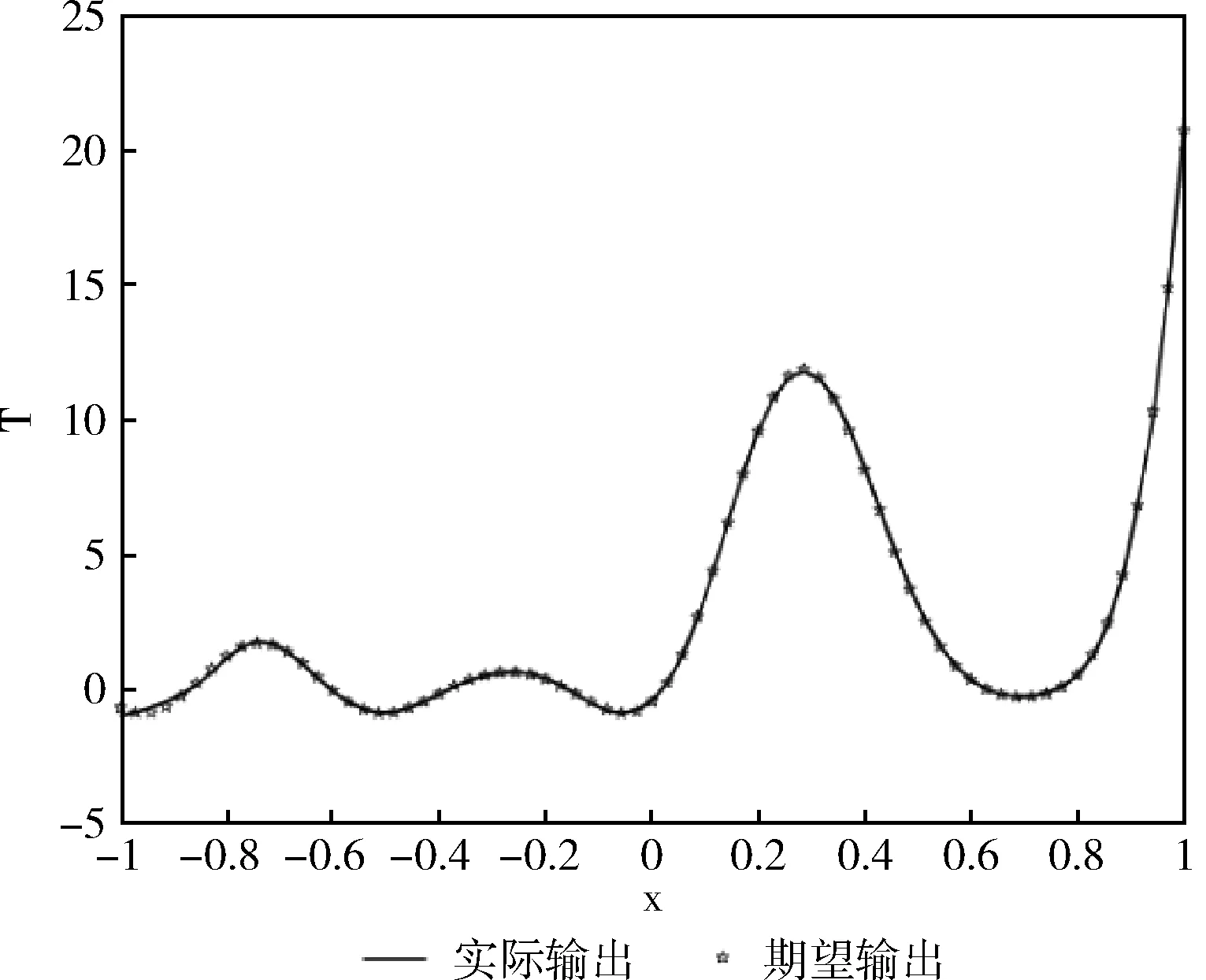
图7 PC逼近T函数
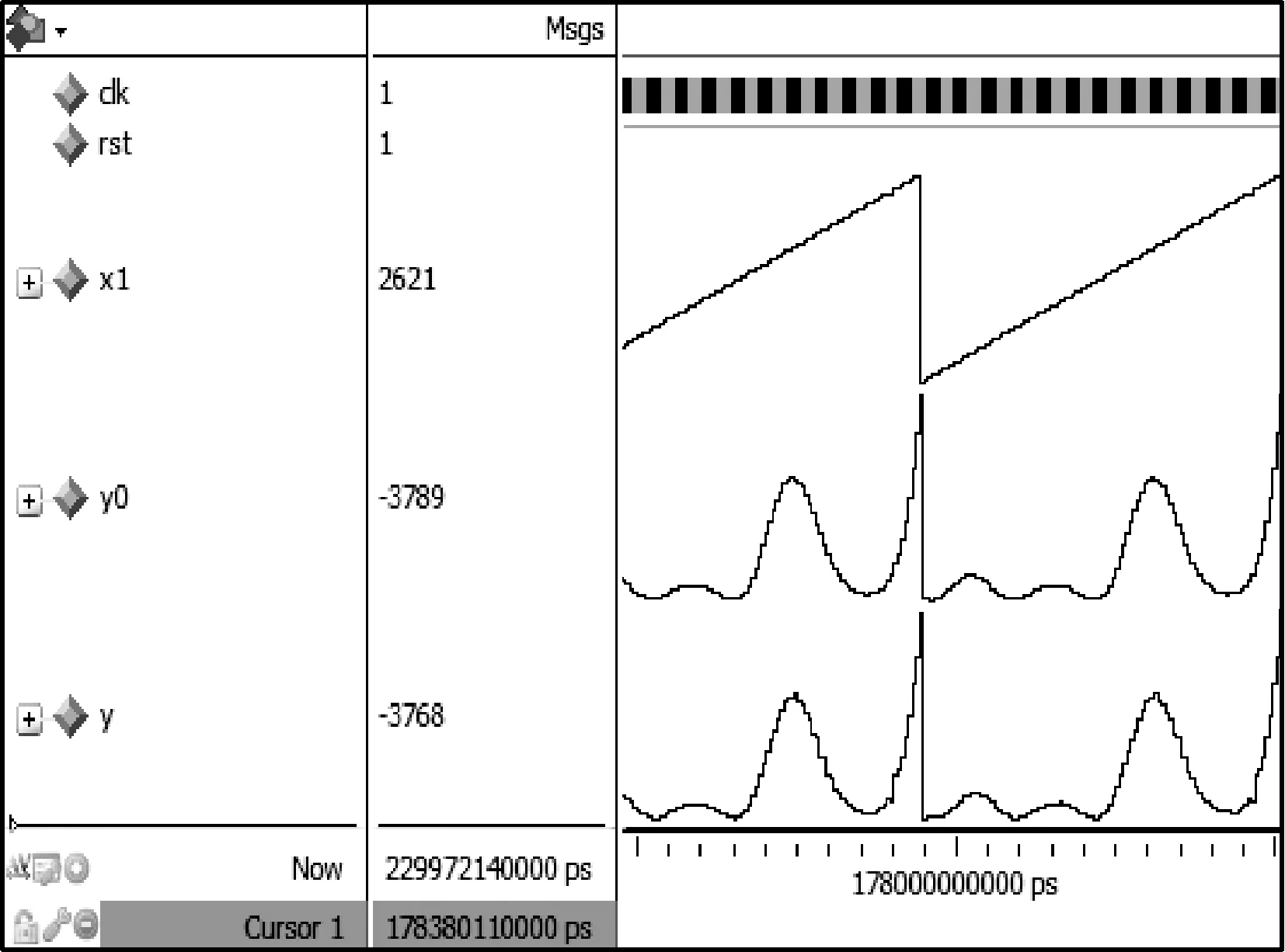
图8 FPGA逼近T函数

资源占比/%ALMs10 192/32 07031.7Pins35/4578DSPS87/87100memory65 536/4 065 2802
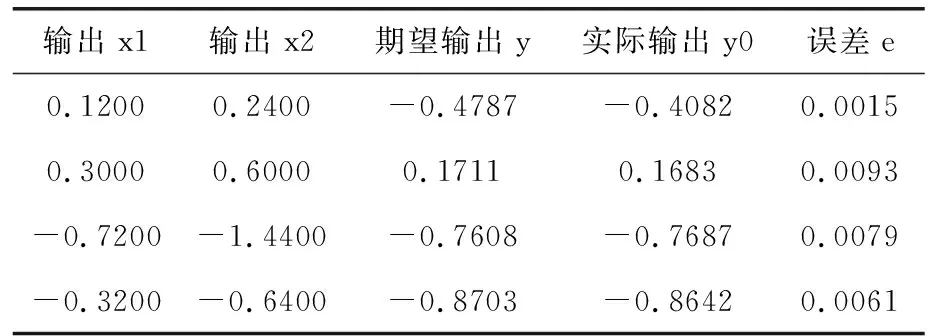
表4 VS2010测试样本
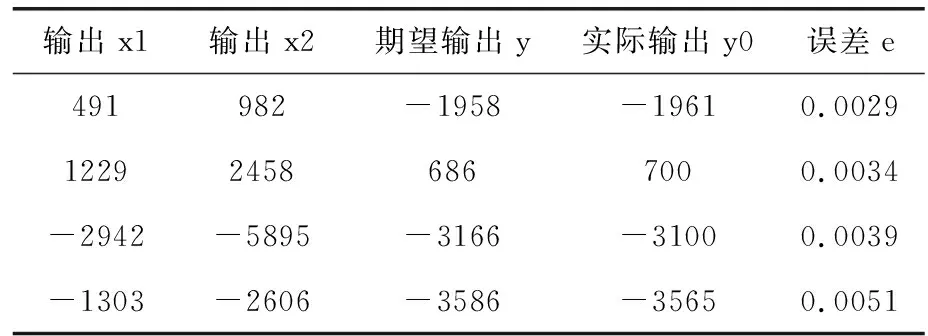
表5 FPGA测试样本
为了证明实验的普遍性,进行了20次的对比实验,每次都由PC随机给出初始权值,将在PC上运用VS2010训练的结果与FPGA芯片训练的结果做对比,结果见表6。
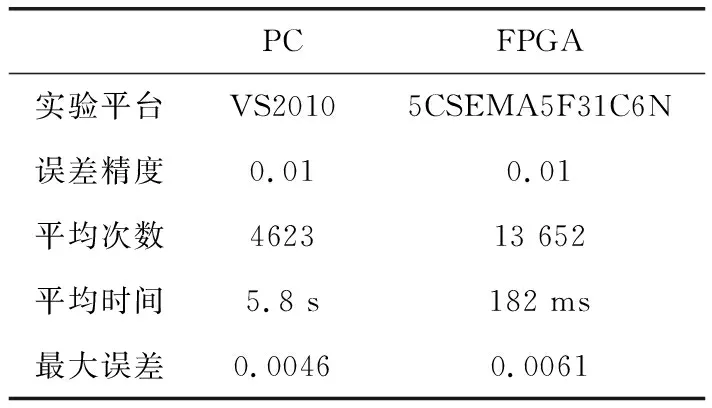
表6 PC与FPGA实现T函数比较
由实验可知,利用FPGA能够充分的发挥BP神经网络的并行性,运用相同的网络结构以及学习速率对相同的样本进行训练时,不但精度可以满足BP神经网络的收敛要求,而且训练速度要远远快于在PC中的训练。
为了验证几个关键性问题的改进可以对FPGA实现BP神经网络进行优化,文章进行了进一步的对比实验。其中一组为前文所提到的改进后的BP神经网络,另一组BP神经网络利用查表法实现激活函数Sigmoid,并在每次迭代后将权值存储在外部存储RAW中,同样的条件下对T函数进行实现,对比结果见表7。
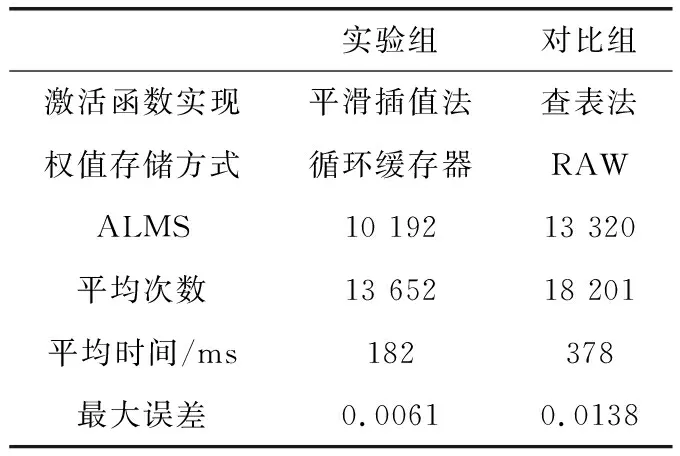
表7 在FPGA中利用不同方式实现T函数对比
根据对比可知,通过对激活函数、存储方式实现的改进,不仅可以减少FPGA实现BP神经网络所消耗的资源,而且可以提高BP神经网络在FPGA中收敛的速度。
3 结束语
基于quartus ii对BP神经网络进行了实现,并在利用Modlsim进行仿真的同时在开发板上进行了板级调试。通过提取的实验数据验证了该方法有效减少了实现激活函数所需要的芯片资源,增加了BP神经网络训练的并行性,提高了网络的训练速度。并通过与通用PC机实现BP神经网络进行精度与效率之间的对比,在精度方面,FPGA上实现BP神经网络的最大误差小于0.01,满足收敛所需要的精度。而在速度方面,FPGA的实现速度要远远超出PC机上的实现速度。
参考文献:
[1]DONG Shuwei,ZHENG Bin,DU Pengfei.Vibration active control system design based on FPGA+DSP[J].Computer Engineering and Design,2015,36(8):2080-2083(in Chinese).[董淑伟,郑宾,杜鹏飞.基于FPGA+DSP的振动主动控制系统设计[J].计算机工程与设计,2015,36(8):2080-2083.]
[2]Ji S,Xu W,Yang M,et al.3D Convolutional neural networks for human action recognition[J].IEEE Trans Pattern Anal Mach Intell,2013,35(1):221-231.
[3]Subirats J,Franco L,Jerez J.C-Mantec:A novel constructive neural network algorithm incorporating competition between neurons[J].Neutral Netw,2012,26:130-140.
[4]YANG Cheng.Research and implementation of artificial neural network based on FPGA[D].Xi’an:Xi’an University of Electronic Science and Technology,2016(in Chinese).[杨程.基于FPGA的人工神经网络的研究与实现[D].西安:西安电子科技大学,2016.]
[5]ZHU Fang.Implementation and application of neural network based on FPGA[D].Guangzhou:Guangzhou University of Technology,2016(in Chinese)[祝芳.基于FPGA的神经网络与应用[D].广州:广州工业大学,2016.]
[6]WANG Meng,CHANG Sheng,WANG Hao.Design of adaptive neural network based on BP neural network[J].Modern Electronic Technology,2016,39(15):115-118(in Chinese).[王蒙,常胜,王豪.一种自适应训练的BP神经网络FPGA设计[J].现代电子技术,2016,39(15):115-118.]
[7]LIU Peilong.Research and design of hardware implementation of neural network based on FPGA[D].Chengdu:University of Electronic Science and Technology,2012(in Chinese).[刘培龙.基于FPGA的神经网络硬件实现的研究与设计[D].成都:电子科技大学,2012.]
[8]GU Zhijian.The research on parallel architecture for FPGA-based convolutional natural networks[D].Harbin:Harbin Engineering University,2013(in Chinese).[顾志坚.基于FPGA的卷积神经网络并行结构研究[D].哈尔滨:哈尔滨工程大学,2013.]
[9]YU Zijian,MA De.FPGA-based accelerator for convolution neural network[J].Computer Engineering,2017,43(1):109-114(in Chinese).[余子健,马德.基于FPGA的神经网络加速器[J].计算机工程,2017,43(1):109-114.]
[10]SHI Changzhen,YANG Xue,WANG Zhensong.Design and realization of high performance parallel FFT processor[J]Computer Engineering,2012,38(2):242-247(in Chinese).[石长振,杨雪,王贞松.高性能并行FFT处理器的设计与实现[J].计算机工程,2012,38(2):242-247.]
[11]ZHOU Jinglong.A FPGA implementation of frequency domain anti jamming algorithm based on a structure of high speed FFT[J].Microelectronics & Computer,2014,31(5):32-35(in Chinese).[周景龙.基于高速FFT结构的频域抗干扰算法的FPGA实现[J].微电子学与计算机,2014,31(5):32-35.]
