基于改进PSO并行算法的梯级水库群生态联合优化调度研究
2018-06-19陈琦琛张严方
陈琦琛,张严方
(1.辽宁天阳工程技术咨询服务有限公司,辽宁 沈阳 110001;2.辽宁泽龙水利实业有限责任公司,辽宁 沈阳 110001)
当前,水库生态调度成为当前国内学者研究河道生态保护的热点问题,为此许多学者展开水库生态调度研究[1- 6],这些成果大都为采用不同类型的优化算法对水库生态调度进行目标优化求解,既保证水库的防洪、兴利的功能,又发挥了水库对下游河道生态改善和保护的作用。近些年来,河道从上至下水库呈现梯级分布,考虑单一水库的生态调度已经不能满足整个河道生态保护的要求,需要对整个河道内的梯级水库进行生态联合的调度研究。对于水库生态联合调度研究,国内已有学者进行研究,这其中PSO并行算法采用自适应优化搜索算法,模型寻优求解精度较高,在目标优化求解领域中得到较为广泛的应用,但是传统PSO算法在目标加速寻优存在局限,使得传统方法的收敛速率较低,为此有学者对传统PSO并行算法进行改进,并在一些水资源优化领域中得到具体应用[7- 9],但是在梯级水库生态联合调度中还未得到相关应用,为此本文引入改进的PSO并行优化算法,对辽宁中东部4座梯级水库进行生态联合调度研究,研究成果可以为梯级水库生态调度优化提供方法参考。
1 改进PSO并行算法的计算原理
改进的PSO并行算法采用并行基函数沿计算中线点逐步向外进行映射求解,模型采用多变量方程对非线性结构函数进行求解,求解方程为:
(1)
式中,XP=[x1,x2,…xH]T,表示为改进算法的输入样本序列;YP—计算目标值;WJ—变量权重系数;D(XP,tj)—计算中心点基函数;tj=[tj1,tj2,…tjm],表示为模型计算中心点的高斯函数值。
改进PSO并行算法结合高斯函数对中心点进行求解,求解方程为:
(2)
式中,σj—高斯中心计算序列的方差值。
改进的PSO并行算法对目标计算误差进行评定,评定方程分别为:
(3)
(4)
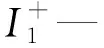
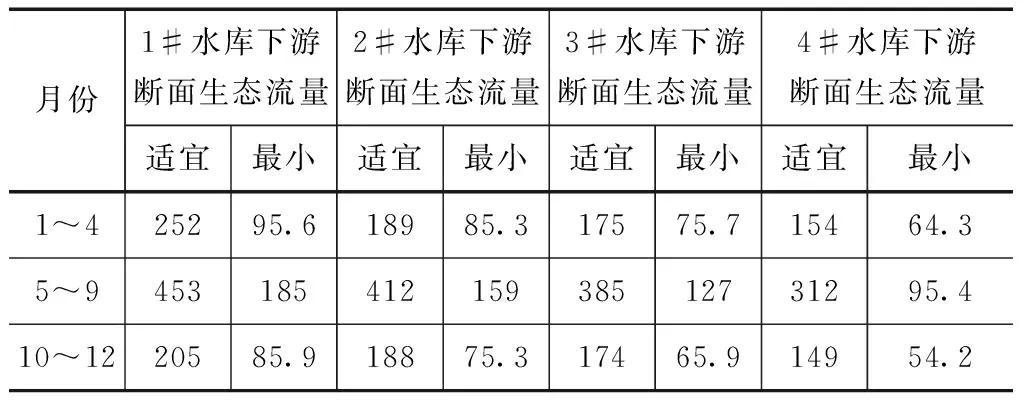
改进的PSO并行算法对变量权重进行计算,权重系数计算方程为:
(5)
式中,δMSE—目标调整值;IK1—广义变量矢量值;H—比例系数值。
改进的PSO并行算法结合梯度下降法加速模型的收敛寻优速率,梯度下降法主要优化模型中心基础函数的标准方差来加速模型的收敛求解:
Δσ=(δMSE2-δMSE1)/α
(6)
[σ0]2=[σ0]1-ηΔσ
(7)
式中,η—模型效率值;[σ0]1和[σ0]2—梯度调整后标准方差值。
水库生态调度综合考虑水库兴利各生态调度,梯级水库生态联合调度的方程为:
(8)
式中,ω1—兴利水量的权重系数;W1—不同水库的兴利水量,106m3;ω2—生态调度权重系数;W2—不同水库的生态调度水量,106m3;Z—调度目标;n—梯级水库的座数。
2 实例应用
2.1 梯级水库主要概况
本文以辽宁中西部4座梯级水库为研究对象,梯级水库主要的特征值见表1。各水库的主要兴利功能为供水和发电,结合各水库的运行调度规则,采用改进的PSO并行算法对梯级水库进行生态联合调度。

表1 梯级水库主要特征值
2.2 梯级水库下游河道典型断面生态流量计算
在进行梯级水库生态联合调度前,需要对各水库不同月份下游河道断面的生态流量进行确定,本文结合适宜生态径流和最小生态径流方法[10]对水库不同时期(丰水期(5~9月)、枯水期(1~4月、10~12月))下游河道典型断面的生态流量进行了确定,计算结果见表2。
表2水库下游河道典型断面生态流量值
单位:m3/s
2.3 不同优化算法的收敛度分析
为对比分析不同优化算法下的收敛寻优速率,结合随机数组序列对各算法不同迭代次数下的粒子多样性和最有粒子适应值进行计算,对比分析结果如图1所示。
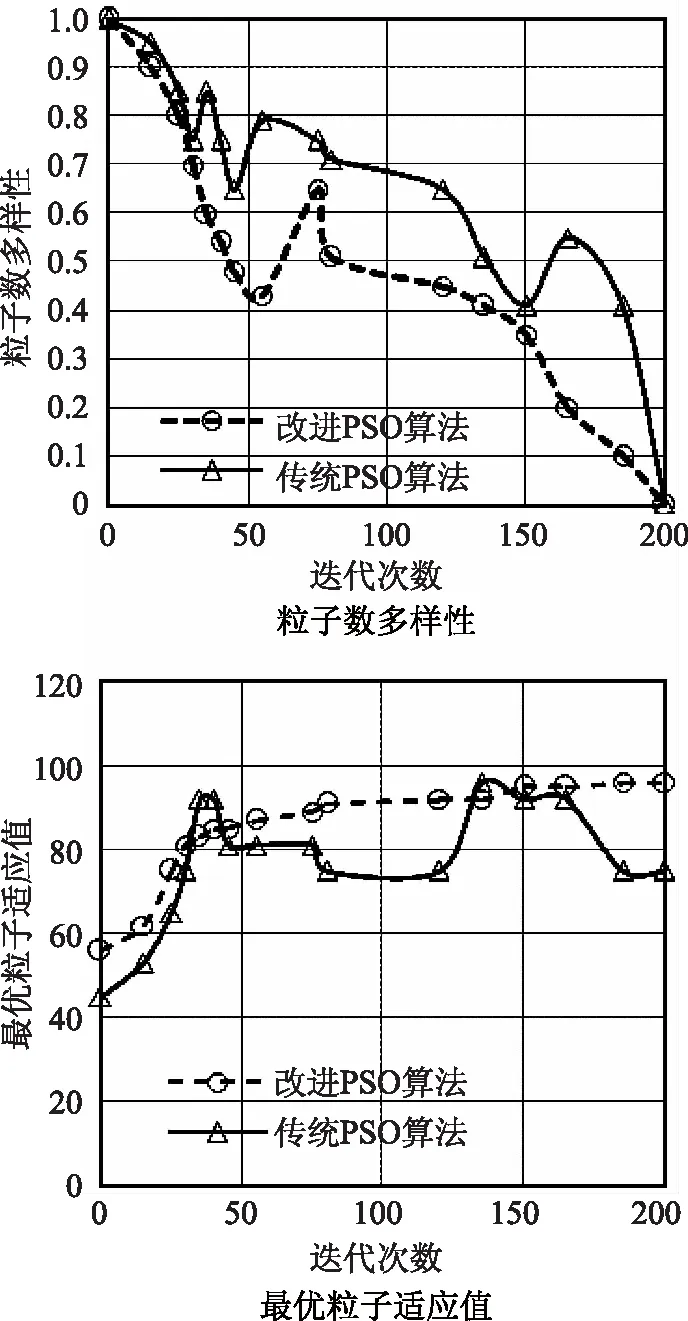
图1 不同算法的收敛度分析结果
从图1中不同算法的粒子多样性对比结果可以看出,相比于传统算法,改进的PSO并行算法寻游下降速率更快,且波动跳跃性更小,改进PSO并行算法的稳定性明显好于传统算法。从最优粒子适应值也可看出,相比于传统算法,改进PSO并行算法的收敛度明显好于传统算法,改进PSO并行算法在最优粒子计算趋于最有解的速率明显快于传统算法,且稳定波动性也明显好于传统PSO算法。这主要是因为改进的PSO并行算法采用梯度下降法并不断调整目标寻优的标准方差值,使得改进算法在目标寻优时收敛速度更快,且更为稳定。
2.4 不同算法下各梯级水库生态联合调度结果
在不同算法收敛精度分析的基础上,本文采用不同算法对梯级水库不同时期(丰水期(5~9月)、枯水期(1~4月、10~12月))的生态联合调度进行水量优化,优化结果见表3、4。
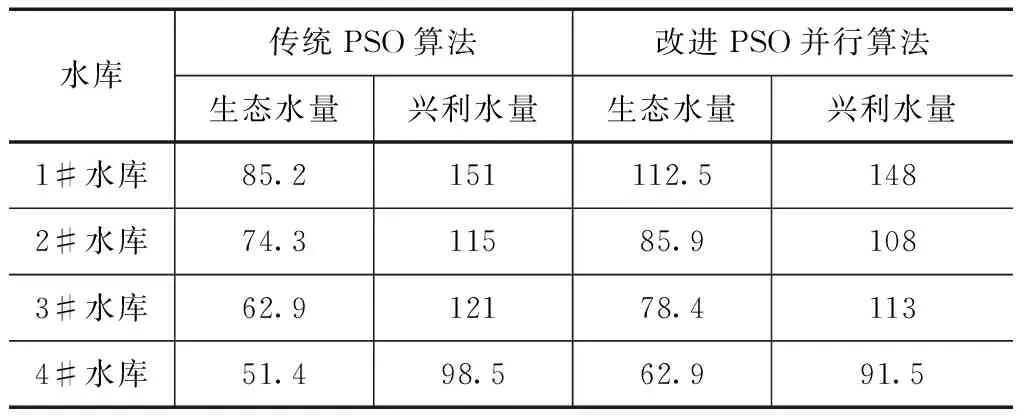
表3 丰水期(5~9月)不同算法下各梯级水库生态联合调度水量优化结果 单位:104m3
表4枯水期(10~12月份和1~4月份)不同算法下各梯级水库生态联合调度水量优化结果单位:104m3
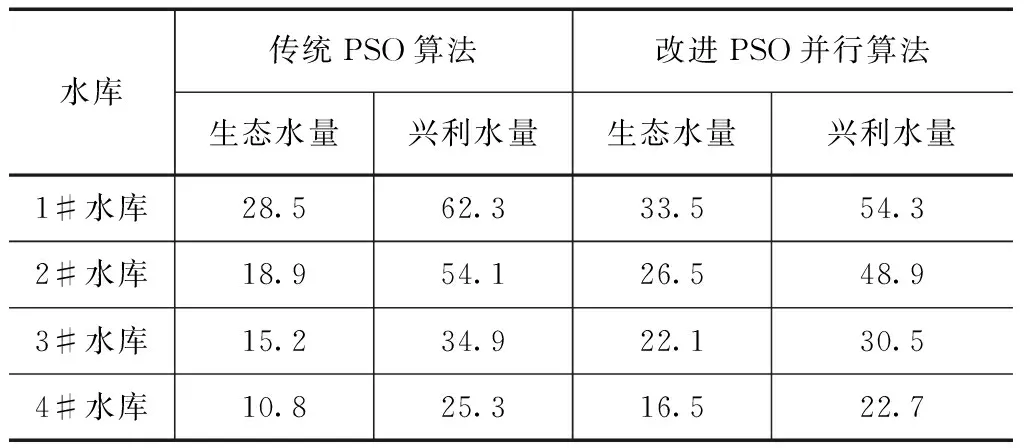
从表3中可以看出,在丰水期(5~9月)和枯水期(10~12月和1~4月)改进的PSO并行算法优化的生态水量多于传统算法,而在兴利水量上,传统算法和改进算法较为接近,表明了改进的PSO并行算法在梯级水库生态联合调度上,即增加了水库的生态调度水量,也没大幅减少水库的兴利水量,梯级水库生态联合调度优化整体结果好于传统算法。
2.5 不同算法下梯级水库下游河道生态保证率对比结果
为定量分析不同算法下梯级水库生态联合调度后其下游河道适宜和最小生态径流的保证率,结合各水库下游河道其下游断面各级生态径流,确定了不同算法下各时期水库下游河道的生态保证率,分析结果见表5、6。
从表5、6中可以看出,采用改进PSO并行算法下各水库下游河道适宜生态和最小生态径流保证率都明显好于传统算法,这表明改进PSO并行算法在梯级水库生态联合调度寻优上有较为明显的改善,改进PSO并行算法下丰水期(5~9月)梯级水库生态联合调度适宜和最小生态保证率分别达到77.9%和82.0%,相比于传统算法,分别提高17.2%和18.0%。在枯水期(10~11月和1~4月)适宜和最小生态保证率分别为66.6%和70.8%,相比于传统算法在枯水期梯级水库生态联合调度下游河道生态保证率也分别提高17.3%和17.5%。河道最小生态径流由于生态需水量小于适宜生态需水量,因此其生态保证率要高于适宜生态径流的保证率。
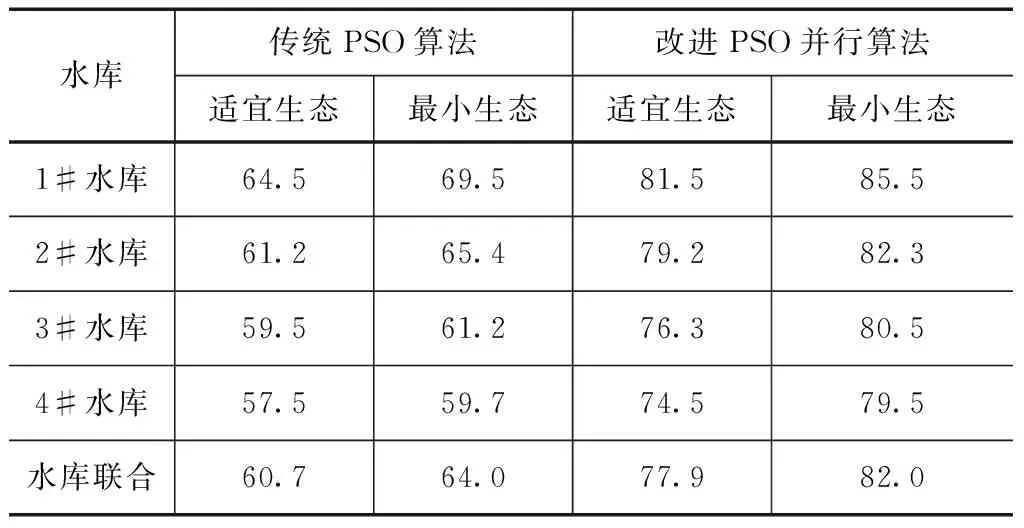
表5 不同算法下水库下游河道丰水期(5~9月)各级生态保证率对比结果 单位:%
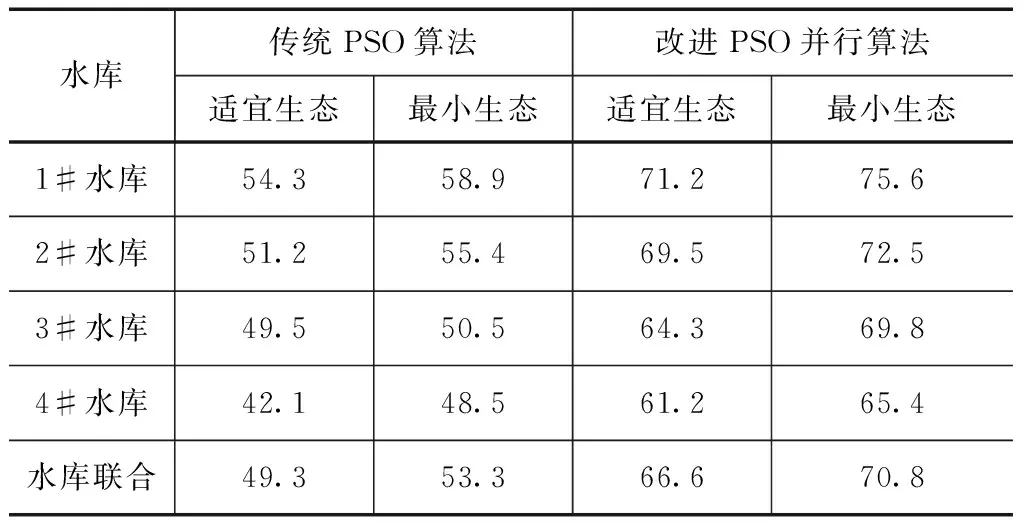
表6 不同算法下水库下游河道枯水期(10~11月和1~4月)各级生态保证率对比结果 单位:%
3 结语
本文采用改进的PSO并行算法对辽宁中西部4座梯级水库的生态联合调度进行研究和探讨,探讨取得以下结论:
(1)改进的PSO并行算法在收敛速率和稳定性上都较传统PSO算法有较为明显的改善。
(2)采用改进PSO并行算法优化后的梯级水库生态水量多于传统算法,并保证了水库的兴利水量;改进PSO并行算法各水库下游河道适宜和最小生态径流保证率都较传统算法提高百分比在17.2%~18.0%之间。
[1] 张洪波. 黄河干流生态水文效应与水库生态调度研究[D]. 西安理工大学, 2009.
[2] 胡和平, 刘登峰, 田富强, 等. 基于生态流量过程线的水库生态调度方法研究[J]. 水科学进展, 2008(03): 325- 332.
[3] 王慧斌. 水库生态调度的内涵与模型探析[J]. 水利规划与设计, 2016(03): 34- 35+107.
[4] 艾学山, 范文涛. 水库生态调度模型及算法研究[J]. 长江流域资源与环境, 2008(03): 451- 455.
[5] 贾瑞红. 水库生态调度的措施及其发展前景[J]. 水利技术监督, 2011(05): 42- 44.
[6] 吴凡. 白石水库生态影响与下泄流量计算分析研究[J]. 水利技术监督, 2016(06): 125- 128.
[7] 孙玥, 关明皓. 改进的PSO-RBF模型在土壤水入渗参数非线性预测中的应用研究[J]. 水利技术监督, 2017(02): 117- 120.
[8] 贺新春, 王翠婷, 汝向文, 丁波. 闸控潮汐河网区水环境调度模型研究[J]. 华北水利水电大学学报(自然科学版), 2018, 39(02): 86- 92.
[9] 徐建新, 吕爽, 樊华. 基于粒子群算法的太子河水量优化调度研究[J]. 华北水利水电大学学报(自然科学版), 2016, 37(03): 32- 35.
[10] 蔡涛, 李琼芳, 王鸿杰, 等. 淮河上游生态需水量计算分析[J]. 河海大学学报(自然科学版), 2009(06): 635- 639.
