基于改进边缘活动轮廓模型的超声图像分割
2018-06-19倪晓航肖明波
倪晓航,肖明波
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
0 引 言
由于超声图像固有的复杂性,医学超声图像分割十分困难[1]。活动轮廓模型,从snake模型开始,基于最小能量函数的观点来分割目标。自1987年Kass等[2]提出snake模型以来,越来越多的研究致力其中。其中水平集方法(level set method,LSM)被广泛关注。水平集方法的分割模型可以视为基于边缘或基于区域的模型,前者根据边缘信息,后者利用区域描述子控制活动轮廓的移动[3]。基于边缘的模型对于灰度不均匀的图像不敏感,但对模糊边界敏感。由于图像中预定义模糊边界附近灰度逐渐变化,ESF不能准确停止轮廓[4]。
为了克服传统ESF在活动轮廓模型中的局限性,我们提出一种方法构建一组稳健型ESF,在分类器中,概率得分来代替预测类标签,因概率得分在区间[0,1],故该方法和模糊分割类似。文献[5,6]所提方法只能依赖贝叶斯准则获得类的概率,而我们的方法更灵活,可以使用任意分类器获取概率得分。同时对于边界分明无模糊灰度值的图像,也能够提取其灰度信息来终止轮廓演化。
1 ESFs的构造
新的ESFs可以由任意分类算法构造,且适用于所有基于边缘的LSM模型。该部分简要介绍一下LSM在图像分割中的应用,然后介绍几种分类算法,k-NN和支持向量机(SVM)以及它们如何构造ESFs。
1.1 基于水平集的分割
水平集方法中,封闭曲线C隐含在一个比它高一维的水平集函数φ(x,y,t)中,该曲线即为水平集函数的零水平集
C(t)={(x,y)|φ(x,y,t)=0}
(1)
水平集方程(level set equation,LSE)定义了隐函数φ的演变,如下式
(2)
(3)
其中,v表示常系数,g是边缘停止函数,常用的g为
(4)
其中,I表示一幅图像,Gσ表示标准差为σ的高斯核。
传统的ESF为避免演变不规则需要重新初始化轮廓[9],但这并不容易,李纯明等提出了距离正则化水平集演化(distance regularized level set evolution,DRLSE)[10],该方法无需重新初始化,通过引入梯度流,把DRLSE用于基于边缘的活动轮廓模型中
(5)
其中,dp由一个势函数p(s)得到,即dp(s)=p′(s)/s,δε为近似Diracδ函数,μ,λ,β都为常数。公式右边三项分别表示:距离正则化能量,长度项和区域项。
边缘停止函数g在式(3)和式(5)中扮演重要角色,既能停止轮廓演化,又可以进一步根据梯度信息在像素分类中决策灰度边界值。
1.2 分类算法的概率得分
我们根据机器学习的方法来构造ESFs,本文研究了两种机器分类方法:k-近邻算法(k-NN)和SVM。
1.2.1k-NN
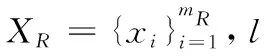
(6)
vj取得最大时即归为j类,其中1≤j≤l,v=(v1,v2,…,vj)。
1.2.2 SVM
SVM是一个监督学习模型,由分类超平面分类数据,给出两类之间的最大间隔[11]。该分类方法根据sign函数class(x)=sgn(h(x)),h(x)表示分离两个类的超平面。对于d维线性可分离数据,超平面可表示为
h(x)=w0TX+b0
(7)
其中,w0∈Rd,R表示最优权矢量,x∈Rd,为待分类数据,b0表示最优偏差。由于原始空间内的数据很难被分离,故引入函数φ(x)将数据映射到高维空间。但找到一个具体的φ比较困难,而核函数K(x,xi)可以按照下式直接计算内积
(8)
其中,αi为SVM估计参数,yi∈{+1,-1},表示xi的对应类别,h(x)的值表示SVM的概率得分,sign函数根据得分预测类别。
分类器的评价得分范围通常在区间[0,1]或[∞,+∞],k-NN分类器评价得分范围为前者,SVM为后者,而后者也可以转化为概率得分的形式。
1.2.3 模糊边缘停止函数
传统的ESFs存在一定缺陷,对模糊边界的分割并不适用,由于梯度渐变,轮廓可能不能在理想边界停止。一幅图像可以由分类器二分类为背景(class 0)和前景(class 1),根据平稳过渡的概率得分找到理想边界。
首先由分类算法对所有像素进行训练以此获得概率得分,概率得分范围为[0,1],然后在目标边界附近,通过平稳过渡,分数由1到0变化(反之亦然)。当执行模糊分类时,若概率得分为0.5,则边界存在的几率最高。就能量最小化而言,得分为0.5的像素点会产生较低的能量。此外,得分为0或1的会产生较高能量,故该区域不是理想边界。根据模糊ESFρ(s):[0,1]→[0,1]
ρ(s)=(2(s-0.5))2
(9)
其中,s表示前景的概率得分,ρ(s)如图1(a)所示,s=0.5时ρ(s)取得全局最小值,将其作为识别目标边界的关键点。

图1 模糊ESFρ(s)
关于ρ的性质,从公式可以看出:值域为[0,1],lims→0ρ(s)=1,lims→0.5ρ(s)=0,lims→1ρ(s)=1;在区间[0, 0.5]ρ(s)单调递减,[0.5, 1]单调递增。其它相同性质的函数也可以作为ρ(s),如
ρ(s)=(cosπs)p0≤s≤1,p=2,4,6,…
(10)
图1(b)为P=2时的ρ(s)图像。
ρ用于调节式(4)的g函数,得到一个新的ESF
gnew=gρ
(11)
超声图像噪声比较大,为了防止轮廓过早停止需要和一个高斯核进行卷积平滑。图像灰度逐渐下降时,ρ接近于0,虽然g大于0,但是模糊ESFρ使gnew接近于0,随后轮廓会在理想边界停止。因此对于模糊边界gnew应取代式(4),此外,仅仅把ρ作为ESF不能使轮廓在理想边界收敛。
2 实验结果及分析
2.1 实验方法及参数设置
为了评估所用算法的有效性,本文选取腰椎超声图像作为实验对象,图片矩阵大小为234×218,由专家绘制一幅标准数据的真实图像作为评价标准如图2(b)所示。本章所有的实验中,实验平台为Windows 7-64位旗舰版的PC,core i3 2.53 GHz处理器,所用算法均在MATLAB R2013a编程环境下仿真实现。具体实验过程如下:把原始超声图像标记为灰、白两处,如图2(a)所示,灰色代表前景,白色表示背景,灰色标记的边界用于初始化轮廓和分类器开始时的训练数据。然后由分类器的结果得到ESF,最后根据DRLSE完成超声图像的分割。默认的参数值μ=0.04,α=1.5,ε=1.5,σ=2.5,λ=3。在模糊k-NN算法中,实验结果表明k>50时效果较好,考虑到边界附近的模糊性,一般将k设为较大的值。这里把k设为99,精确地覆盖一百个不同的隶属度且在前景和背景之间实现平稳过渡。由于SVM算法的核函数是线性的,这里把尺度参数设为1,生成一个3×3的图像补丁作为特征向量,并用于所有的实验中。初步实验结果表明式(9)和式(10)效果类似。

图2 初始化轮廓和真实图像
为验证算法的优越性,将不同分割算法与本文提出的方法进行比较,如经典C-V模型以及李纯明模型(Li)。对于C-V模型,各个参数如迭代次数、时间步长、长度项系数、前景和背景权重等参照文献[12,13]来设置;对于Li,参数和我们所提方法一致,当迭代次数达到我们预定义的数量时,轮廓停止,分割结束。采用两种评价指标来比较算法的有效性,Jaccard指数(JI)和Dice系数,也被称为相似性系数(SI)。若A和B分别表示分割图像和真实图像,则JI为(A∩B)/(A∪B),SI为(2|A∩B|)/(|A|+|B|)。
2.2 分割结果
腰椎超声图像分割结果,如图3(灰色实线表示分割轮廓,灰色虚线为真实轮廓,黑色虚线表示初始轮廓),几种不同算法的效果对比见表1,表1给出了各个算法的平均耗时和JI、SI,可以看出本文提出的方法平均耗时最短、准确度最高。C-V模型在处理灰度不均匀的图像时效果不佳,而李纯明模型大大超出预定义边界。针对这些问题,本文的方法都能够很好解决,证实了该方法较于传统基于边缘的主动轮廓模型的优越性。
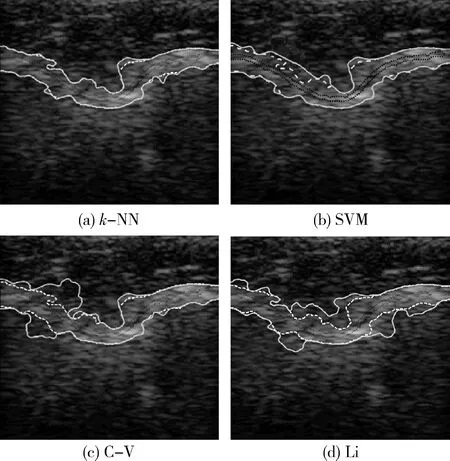
图3 几种算法的分割结果
显然,在预定义边界存在的前提下,ρ函数起着决定性作用,当分数处于决策边界时,它产生一个最小值,若边界清晰,没有模糊值,它能够保留图像的灰度信息。gnew函数可以兼顾这两个优势,能够更加准确地分割图像。本文所提出的方法比较灵活,ESFs可以由任意的分类器构造。基于式(10)的不同P值对超声图像处理,也得出了相应的数据,见表2,结果表明与式(9)准确度相近。
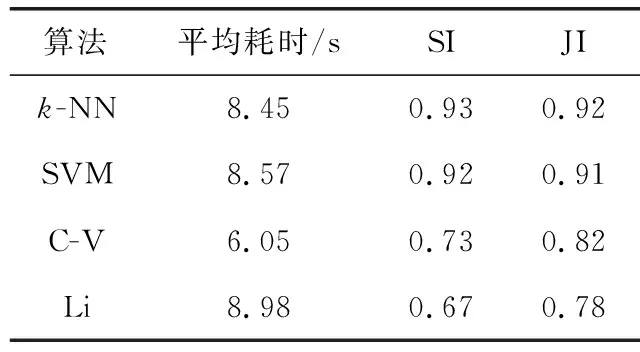
表1 不同算法下的分割效果
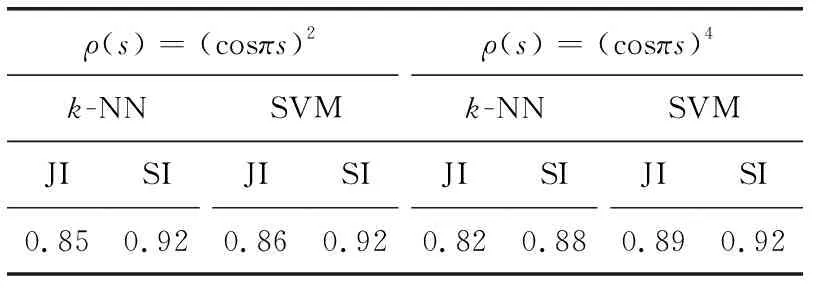
表2 两种ρ函数下的分割准确度
基于边缘的活动轮廓模型对于初始化比较敏感,而概率得分对训练数据敏感。本文实验中,前景初始化不仅初始化轮廓,而且学习了前景像素点。值得注意的是,合适的初始化十分关键,尤其对于灰度不均匀的图像。训练数据也应该覆盖前景来产生一个比较好的分割效果。图4表明不同初始化轮廓下的分割结果。
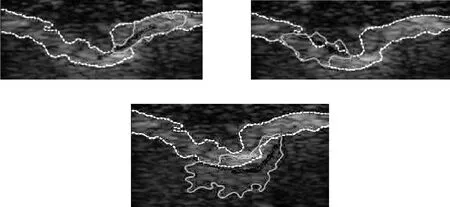
图4 不同初始化轮廓的分割结果
3 结束语
本文提出的方法,构建一组稳健型ESFs用于基于边缘的活动轮廓模型,能够准确检测模糊边界。该方法利用图像梯度值的边缘信息以及分类器的概率得分来实现基于边缘的活动轮廓模型。此外,ESFs可以由任意分类器构造,相较于其它模型更加灵活。具体实验中通过DRLSE结合k-NN或SVM对医学超声图像进行处理,对比实验结果表明,该算法能够有效分割模糊边界轮廓,且分割速度较快。
参考文献:
[1]WEN Qiaonong,LIU Zengli,WAN Suiren,et al.Ultrasound image segmentation based on graph-model of curve length constraint[J].Journal of Computer-Aided Design & Computer Graphics,2014,26(4):545-552(in Chinese).[文乔农,刘增力,万遂人,等.超声图像分割的曲线长度约束的图模型方法[J].计算机辅助设计与图形学学报,2014,26(4):545-552.]
[2]CHEN Lichao,NIU Yumei,PAN Lihu,et al.Research advances on Snake model[J].Application Research of Compu-ters,2014,31(7):1931-1936(in Chinese).[陈立潮,牛玉梅,潘理虎,等.Snake模型的研究进展[J].计算机应用研究,2014,31(7):1931-1936.]
[3]LI Huiguang,SUN Sijia.Level set algorithm of combining edge and region information[J].Computer Engineering and Applications,2014,50(18):175-177(in Chinese).[李惠光,孙思佳.融合边缘与区域信息的水平集分割算法[J].计算机工程与应用,2014,50(18):175-177.]
[4]WANG Pei,ZHOU Xin,PENG Rongkun,et al.Active contour model based on edge and region attributes for target contour extraction in SAR image[J].Journal of Image and Graphics,2014,19(7):1095-1103(in Chinese).[王沛,周鑫,彭荣鲲,等.结合边缘和区域的活动轮廓模型SAR图像目标轮廓提取[J].中国图象图形学报,2014,19(7):1095-1103.]
[5]Melin P,Gonzalez C I,Castro J R,et al.Edge-detection method for image processing based on generalized type-2 fuzzy logic[J].IEEE Transactions on Fuzzy Systems,2014,22(6):1515-1525.
[6]Li C.A likelihood and local constraint level set model for liver tumor segmentation from CT volumes[J].IEEE Transactions on Biomedical Engineering,2013,60(10):2967-2977.
[7]Anchalo Bensiger S M,Kumar S N.A semi automatic geometric active contour model using distance regularized term for segmentation of abdominal organs on CT images[C]//IEEE International Conference on Engineering and Technology,2016:753-757.
[8]Tao W.Iterative narrowband-based graph cuts optimization for geodesic active contours with region forces (GACWRF)[J].IEEE Transactions on Image Processing,2012,21(1):284-296.
[9]ZHOU Ben,HE Chuanjiang,YUAN Ye.Edge-based active contour model with adaptive varying stopping function[J].Application Research of Computers,2012,29(1):366-368(in Chinese).[周奔,何传江,原野.结合自适应变化停止函数的边缘活动轮廓模型[J].计算机应用研究,2012,29(1):366-368.]
[10]Ngo T A,Carneiro G.Lung segmentation in chest radiographs using distance regularized level set and deep-structured learning and inference[C]//IEEE International Conference on Image Processing.IEEE,2015:2140-2143.
[11]Cortes C,Vapnik V.Support-vector networks[J].Mach Learn,1995,20(3):273-297.
[12]Mao C,Wan S.A water/land segmentation algorithm based on an improved Chan-Vese model with edge constraints of complex wavelet domain[J].Chinese Journal of Electronics,2015,24(2):361-365.
[13]Getreuer P.Chan-Vese segmentation[J].Image Processing on Line,2012,2:214-224.
