改进的自适应Canny边缘检测算法
2018-06-19段锁林殷聪聪李大伟
段锁林,殷聪聪,李大伟
(常州大学 机器人研究所,江苏 常州 213164)
0 引 言
边缘检测是很多其它图像处理技术的基础[1]。传统的边缘检测算法有Roberts、Sobel、Prewitt、Kirsch、Canny等。其中Canny算法相对于其它几种算法具有较好的去噪能力和较高的检测精度,应用范围较广[2]。但是,传统Canny算法存在需要设定参数、椒盐噪声环境下检测效果不佳等问题。近年来,许多学者针对Canny算法存在的问题进行了改进。文献[3]提出用窗口大小为3×3的改进后中值滤波器替代高斯滤波器,减少了运算量,但是对不同程度的椒盐噪音适应性较差且对高斯噪声的滤波效果不佳;文献[4,5]提出用自适应中值滤波器替代高斯滤波器,对椒盐噪声自适应性较好,但是运算量较大,对高斯噪声的去噪效果不佳;文献[3,6]在计算梯度时将模板扩大为3×3,增加计算45°和135°方向的梯度,增加了算法的抗噪性,但是没有充分利用45°和135°方向的数据来计算梯度的方向;文献[4,7]引入Otsu算法根据像素梯度值的分布情况计算高、低阈值,增加了算法的自适应性,但是传统Otsu算法需要遍历每个像素梯度等级来确定最大类间方差值,效率较低。
针对上述问题,通过改进自适应中值滤波器、增加梯度计算模板和在Otsu算法中引入二分查找法等手段来改进传统Canny算法。实验结果表明,该算法在椒盐噪声和高斯噪声环境下都有较好的边缘检测效果,自适应性强,在一定程度上减少了算法的计算机耗时。
1 传统Canny算法存在的问题
(1)Canny算法采用二维零均值高斯滤波器对图像进行去噪处理,滤波器函数表达式如下
(1)
式中:σ——高斯滤波器分布参数,当σ取值较小时,边缘定位精度较高,但抑制噪声能力差。在噪声较大时,需要增大σ的值和增大模板,但会使边缘位置偏离实际位置,边缘定位精度降低[8]。因此,需要根据图像含有噪声的具体情况人为设置σ的取值大小,同时,高斯滤波器对椒盐噪声的滤波效果不佳。
(2)传统Canny算法采用2×2大小的模板来计算平滑后灰度图像的梯度幅值和梯度方向。其中,点(i,j)处的灰度值为I(i,j),则水平和垂直两个方向上的梯度值分别为
Gx(i,j)=[I(i,j+1)-I(i,j)+I(i+1,
j+1)-I(i+1,j)]/2
(2)
Gy(i,j)=[I(i,j)-I(i+1,j)+I(i,
j+1)-I(i+1,j+1)]/2
(3)
此时,点(i,j)处的梯度幅值G(i,j)和梯度方向θ(i,j)分别为
(4)
(5)
由于采用了2×2梯度计算模板,使得对噪声比较敏感,容易检测出很多伪边缘和丢失真实边缘,造成边缘定位精度降低,并且所计算出来的其实是内插点(i+1/2,j+1/2)处的梯度幅值和方向[6]。
(3)传统Canny算法根据双阈值从候选边缘点中寻找最终的边缘点。双阈值的选择需要根据图像梯度分布的具体情况预先设定高阈值Th和低阈值Tl。对于边缘强度不同的图像,用同一组高、低阈值分割,效果相差很大[9]。因此,传统Canny算法对边缘强度分布不同的图像,适应性差。
2 改进的自适应Canny边缘检测算法
针对上文所分析的问题,在已有的改进方法基础之上,提出了进一步的改进方法,旨在提高边缘检测算法的自适应性,降低运算量,提高算法的实时性。
2.1 改进的自适应中值滤波算法
传统中值滤波是基于数据整体排序的方法找出最大值、最小值和中值,随着滤波窗口的增大,运算量会急剧增加,并且对高斯噪声的滤波效果不佳。利用分治法思想和相邻窗口排序信息相关性的原理改进传统自适应中值滤波器,可以大大减小排序时的比较次数,再结合IMF(improved median filter)算法可以使其对高斯噪声也具有较好的滤波效果[10]。具体改进方法如下:
设滤波窗口为Wn,窗口中像素点的灰度值为aij,则有
(6)
首先利用分治法思想对Wn中元素进行排序[11]。将Wn中每一列分别进行由小到大排列得到新的矩阵Xn,使得Xn的第1行为Wn中每一列的最小值,第2n-1行为Wn中每一列的最大值,第n行为Wn中每一列的中值。接着对Xn中的第1行、第n行和第2n-1行分别进行由小到大排列得到矩阵Yn,则Yn中的a11和a(2n-1)(2n-1)分别是Wn中的最小值和最大值,ann是Wn中的近似中值。实验结果表明,这样得到的近似中值不影响滤波效果。若滤波窗口为N×N,则传统中值滤波算法最坏需要N2(N2-1)/2次比较才能找到中值,通过上述改进后最坏只需要N(N-1)(N+3)/2次比较计算。
为了进一步降低运算量,提高算法实时性,根据相邻滤波窗口排序信息相关性的原理,利用前一个滤波窗口已排列好的数据代入下一个滤波窗口,减少下一个滤波窗口的比较次数。设当前滤波窗口为经过上文重新排序后的Y(i,j),下一个滤波窗口为沿水平方向往右移动一个像素点的Y(i,j+1)。如图1所示,Y(i,j+1)为Y(i,j)移除其第1列数据,同时移入下一列新像素构成的新的滤波窗口。
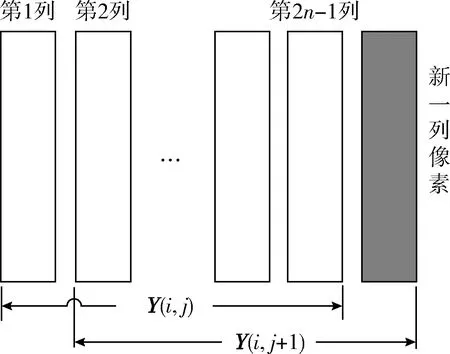
图1 滤波窗口平移
由于新的滤波窗口Y(i,j+1)中除了最后一列是新移入的数据,其它每一列都是在Y(i,j)中已经排序好的数据,所以只要将Y(i,j+1)中最后一列数据由小到大排序后,再把Y(i,j+1)第1行、第n行和第2n-1行分别进行由小到大排列,即可得到最小值、最大值和近似中值。由于Y(i,j+1)中第1行、第n行和第2n-1行的前2n-2个数据在Y(i,j)中已经排列好了,是一组有序的数据,所以最坏只需要2n-2次比较即可完成排序。结合上一步的改进方法,对于大小为N×N的滤波窗口最坏只需要N(N-1)/2+3(N-1)次比较就可以找到最小值、最大值和近似中值。由此可知,改进后算法第1步迭代计算的复杂度为O(N3)=N(N-1)(N+3)/2,第2至k步迭代计算的复杂度为O(N2)=N(N-1) /2+3(N-1)。当迭代次数k远大于1时,改进后算法最差平均复杂度为O(N2)。而传统中值滤波的复杂度为O(N4)=N2(N2-1)/2。可见,改进后的算法复杂度由O(N4)降低到了O(N2),大大降低了运算量。以大小为5×5的滤波窗口为例,Y(i,j+1)最坏只需要进行3×(5-1)+5×(5-1)/2=22次比较即可得到最小值、最大值和近似中值。相对于传统中值滤波的25(25-1)/2=300,改进后的算法把比较次数减小到原来的1/13左右,且窗口越大越能体现出该改进方法的优势。
通过上述改进后,可以快速找到窗口内的最小值、最大值和近似中值。接着,借用文献[10]中提到的IMF算法思想对窗口的像素点的灰度值做加权平均,目的是使滤波器对高斯噪声也有一定的滤波效果。假设滤波窗口大小为N×N,对像素点(m,n)进行滤波。先用上文改进后的方法找到窗口内的最小值amin、最大值amax和近似中值amed,然后计算出窗口内各像素灰度值a(i,j)与amed的方差D(i,j),接着使用如下公式计算各像素点灰度的权重r(i,j)
(7)
最后的滤波输出为
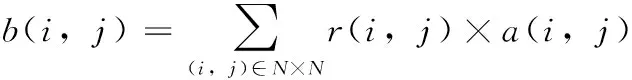
(8)
经过上述改进后的自适应中值滤波结合了均值滤波的优点,在加权求和时像素点的灰度值与中值相差越大,其权重越小,这样不仅可以滤去椒盐噪声,还可以抑制高斯噪声。
改进后的自适应中值滤波具体实施步骤如下:
步骤1 设滤波窗口大小为w=3;
步骤2 按改进后的方法计算当前窗口内灰度值的最小值amin、最大值amax和近似中值amed;
步骤3 如果amin 步骤4 如果w小于或等于允许的最大窗口,则跳转到步骤2,否则用当前窗口内的近似中值amed替换当前像素点的灰度值,即a(i,j)=amed; 步骤5 如果amin 实验验证,与传统Canny算法和文献[3]中的方法相比,改进后的自适应中值滤波器对椒盐噪声和高斯噪声都具有较好的去噪效果,自适应性、抗噪性有较大的提高。 本文在文献[3]的基础上进一步改进梯度的计算方法,借鉴Sobel算子的思想,增加45°和135°方向梯度计算模板,如图2所示。 图2 改进后梯度模板 根据上述改进后模板可计算得出4个方向的梯度幅值:Gx(i,j)、Gy(i,j)、G45(i,j)和G135(i,j)。具体计算方式如下 Gx(i,j)= {[I(i+1,j-1)+2I(i+1,j)+ I(i+1,j+1)]-[I(i-1,j-1)+ 2I(i-1,j)+I(i-1,j+1)]}/4 (9) Gy(i,j)= {[I(i-1,j+1)+2I(i,j+1)+ I(i+1,j+1)]-[I(i-1,j-1)+ 2I(i,j-1)+I(i+1,j-1)]}/4 (10) G45(i,j)= {[2I(i+1,j+1)+I(i+1,j)+ I(i,j+1)]-[2I(i-1,j-1)+ I(i-1,j)+I(i,j-1)]}/4 (11) G135(i,j)= {[2I(i-1,j+1)+I(i-1,j)+ I(i,j+1)]-[2I(i+1,j-1)+ I(i+1,j)+I(i,j-1)]}/4 (12) 由上述得到的4个梯度可以合成当前像素点灰度值在横竖两个方向上总的梯度,计算方式如下 (13) (14) 所以,当前像素点灰度值的梯度幅值G(i,j)和梯度角度θ(i,j)分别为 (15) (16) 改进后的梯度计算方法充分考虑了8邻域内的梯度情况,使得梯度的计算更为准确。同时,所计算出来的是像素点(i,j)处梯度,而不是内插点的梯度。 Canny算法根据双阈值从候选边缘点中寻找最终的边缘点,因此,高、低阈值的设定会直接影响边缘检测的效果。文献[3]采用迭代法来求取高、低阈值,解决了传统Canny算法需要人为设定高、低阈值的问题。但是用文献[3]所提出的迭代法计算非极大值抑制后的梯度图像高、低阈值时,会出现低阈值偏低、高阈值偏高的情况。具体如图3、图4所示中两条垂直的虚线,分别是迭代法计算出来的对梯度分布曲线的分割线。为了直观起见,本文将梯度分布曲线与类间方差分布曲线做在同一张图中,且只统计非0梯度值。图3、图4中两条垂直的点划线,分别是Otsu法计算出来的对梯度分布曲线的分割线。在对lena图像和rice图像的梯度图像进行分割时可以发现Otsu算法计算出的高阈值可以较好地将梯度值较大的部分和梯度值较小的部分分割开来,其低阈值可以把绝大部分梯度值较小的部分分割开来。但是迭代法的分割效果明显不佳,因为文献[3]提出的迭代法本质上是将梯度值较小的部分的梯度均值作为低阈值,把梯度值较大的部分的梯度均值作为高阈值。这样迭代法计算出来的高阈值就偏高,使得部分真实边缘丢失;低阈值就偏低,使得边缘连接时会检测出较多的伪边缘。 图3 lena梯度图像类间方差分析 图4 rice梯度图像类间方差分析 Otsu算法是日本学者大津展之提出的一种对图像进行分割的算法。Otsu算法遍历所有灰度等级对应的类间方差值,取使类间方差最大的灰度值作为阈值[12]。因此,Otsu算法能够根据图像灰度的分布情况自适应地计算出合适的分割阈值。将其应用于Canny算法中,可以自适应地计算出非极大值抑制后的梯度图像的分割阈值。具体操作如下: 设大小为M×N的灰度图像中某一点的灰度值为f(x,y),其取值范为[0,L-1],表示图像中有L个灰度级数。灰度值为k的像素点出现的概率用p(k)表示,如式(17)所示 (17) 假设:选择一个阈值t(0 前景占整个图像的比例 (18) 背景占整个图像的比例 (19) 前景灰度均值 (20) 背景灰度均值 (21) 整幅图像灰度均值 μ=w0(t)μ0(t)+w1(t)μ1(t) (22) 前景与背景间的类间方差为 g(t)=w0(t)(μ0(t)-μ)2+w1(t)(μ1(t)-μ)2= (23) 在非极大值抑制(NMS)后的梯度图像中,让梯度值t在[0,L-1]范围内依次取值,使类间方差g(t)最大的t值即为最佳分割阈值。该阈值作为Canny算法中的高阈值Th,再利用Tl=0.5Th求出低阈值Tl[12]。 文献[4,13]等均将Otsu算法运用于Canny算法中,来计算高、低阈值。但是,传统Otsu算法需要遍历整个灰度等级来计算类间方差值,运算量大,效率低。因此,提出利用二分法查找原理改进传统Otsu算法,减小运算量。利用二分法查找原理的前提是被查找表必须具备有序性[14]。因为Otsu算法中需要查找的是类间方差表,所以以边缘信息丰富的lena图像和边缘信息简单的rice图像为例,分析非极大值抑制后的梯度图像前景与背景间方差的有序性。由图3、图4分析可知,无论图像的边缘信息是否丰富,类间方差分布曲线都是单峰值曲线,且由类间方差的统计学意义可知,不存在局部极大值。在非极大值抑制后的梯度图像中,所取梯度阈值离最佳分割阈值越近,前景与背景间的方差越大;反之,方差越小。只有当所取梯度阈值为最佳阈值时,类间方差最大。因此,非极大值抑制后的梯度图像中,每一个梯度等级的类间方差值都具备次序性,满足二分法查找原理的使用条件。 基于上述分析结果,可以利用二分法查找原理改进传统Otsu算法。使用3个相邻的梯度值作为查找窗口,每次查找后计算窗口内的3个类间方差值,并比较大小以确定下一次的查找范围。图5为查找方式。 图5 二分法查找 具体实施步骤如下: (1)求整幅梯度图像的梯度均值T,用T将梯度图像分为两个部分,计算出梯度值小于等于T部分的梯度均值T1和梯度值大于T部分的梯度均值T2。由类间方差的统计意义可知,最佳阈值不可能落在区间[T1,T2]之外,因此,将区间[T1,T2]作为搜索域。 (2)取T1和T2的平均值Tm,以及Tm两个相邻的梯度值Tm-1和Tm+1作为阈值,根据式(23)分别计算出对应的类间方差值g(Tm-1)、g(Tm)和g(Tm+1)。 (3)如果g(Tm-1) (4)重复步骤(2)、(3),直到搜索到最佳阈值。该阈值作为Canny算法中的高阈值Th,低阈值Tl=0.5Th。 实验发现使用上述查找方式后,图3、图4的非极大值抑制后图像分别只需21次和18次计算类间方差值,即可找到最佳阈值,比传统方法的255次大大减少了计算量。 本文的实验平台是处理器主频2.53 GHz,内存4 GB,显存1 GB的个人计算机。算法采用MATLAB R2014b编程实现。选取lena图像和rice图像来做实验,并统计传统Canny算法、文献[3]算法和本文算法各自所需要的时间,对应的高、低阈值以及峰值信噪比(PSNR),作为分析对比的依据。其中,传统Canny算法的高斯滤波参数σ设为2,滤波窗口设为3×3,高阈值Th设为0.10,低阈值Tl设为0.05。为了验证本文算法的抗噪性,在实验一中分别加入密度为0.5%和3%的椒盐噪声,在实验二中分别加入方差为10和30的零均值高斯噪声。实验结果如图6、图7所示。 在实验一中,当椒盐噪声密度为0.5%时,传统Canny算法检测结果中混入了较多的椒盐噪声点。文献[3]算法虽然滤去了椒盐噪声点,但是由于其计算出来的高阈值偏高(见表1),导致丢失了很多真实边缘,检测结果中丢失了大量的细节。本文算法不仅滤除了椒盐噪声点,还保留了较多的细节。当椒盐噪声密度为3%时,传统Canny算法已经不能有效地检测边缘了。文献[3]算法由于采用3×3固定窗口大小的中值滤波,所以对于高浓度的椒盐噪声滤波效果不佳,检测结果中混入了部分椒盐噪声点。本文算法采用改进后的自适应中值滤波,在高浓度的椒盐噪声环境下依然有不错的边缘检测效果。在峰值信噪比(peak signal to noise ratio,PSNR)统计图中,如图8所示,可见在不同密度椒盐噪声环境下,本文的算法的峰值信噪比最高。文献[3]算法随着噪声密度的增加,峰值信噪比下降严重。 表1 高、低阈值统计 图6 实验一 图7 实验二 图8 椒盐噪声环境下PSNR统计 在实验二中,当高斯噪声方差为10时,传统Canny算法和本文算法都有较好的检测效果。文献[3]算法由于采用中值滤波,对高斯噪声去噪效果不佳,在检测结果中混入了部分噪声点。当高斯噪声方差为30时,本文算法依然有较好的检测结果,传统Canny算法的检测结果中混入了少部分噪声点,原因是其采用的是滤波参数固定的高斯滤波器,不能对不同强度的高斯噪声做出自适应调整。文献[3]算法的检测结果中混入了大量噪声点,原因是其采用的3×3固定窗口的中值滤波器对高强度高斯噪声几乎没有效果,并且其计算出来的低阈值偏低(见表1),容易检测出伪边缘。高斯噪声环境下峰值信噪比(PSNR)统计如图9所示,从图中可以看出文献[3]算法的峰值信噪比最低。 图9 高斯噪声环境下PSNR统计 在上述实验中由于本文算法和文献[3]算法所采用的阈值计算方法不同,使得各自的分割效果也不一样。高、低阈值统计见表1,可见迭代法计算出来的低阈值比Otsu算法计算出的低阈值要小,而高阈值比Otsu算法计算出的高阈值要大。结合图3、图4的分析结果可知,这就是在实验中文献[3]算法容易检测出伪边缘和丢失真实边缘的原因。而改进后的Otsu算法可以较好地分割梯度图像,同时,与文献[4,13]直接使用Otsu算法相比,在阈值计算环节计算量大为降低,提高了算法效率。 表2是各算法在不同种类和不同强度噪声环境下所用时间的统计对比。从表2中可以发现文献[3]耗时最少,但是其边缘检测效果不佳。本文算法耗时比传统Canny算法增加13%左右,但是基本能满足实时性的使用要求。虽然本文算法耗时稍有增加,但是对不同种类和不同强度的噪声都具有较好的去噪效果,且能够自适应地计算出梯度图像的高、低阈值,具有较强的自适应性和抗噪性。 表2 各算法运行时间/ms 针对传统Canny算法存在的问题和文献[3]中改进的中值滤波对高斯噪声滤波效果不佳、迭代法计算阈值不准确等问题,本文做出了如下改进: (1)利用分治法思想和相邻窗口排序信息相关性的原理,并结合IMF算法改进传统自适应中值滤波器,使其对椒盐噪声和高斯噪声都具有较好的去噪效果,且相对于传统自适应中值滤波器,大大减少了排序次数。 (2)借鉴Sobel算子的思想,充分利用8邻域范围内的数据计算梯度幅值和方向,使得梯度的计算更为准确。 (3)利用二分法查找原理改进Otsu算法来计算梯度幅值的高、低阈值。相对于文献[3]中的迭代法,改进后Otsu算法阈值计算更为合理,且大大减少了运算量。 实验结果表明,本文改进后的算法具有较强的自适应性及良好的抗噪性,在一定程度上减少了算法的计算机耗时,提高了Canny边缘检测方法的实时性。 参考文献: [1]ZUO Fei.Digital image processing:Principles and practices[M].Beijing:Electronic Industry Press,2014:148-149(in Chinese).[左飞.数字图像处理:原理与实践[M].北京:电子工业出版社,2014:148-149.] [2]CUI Liqun,ZHANG Yue,TIAN Xin.Fusion of double threshold and improved morphological edge detection[J].Computer Engineering and Applications,2017,53(9):190-194(in Chinese).[崔丽群,张月,田鑫.融合双阈值和改进形态学的边缘检测[J].计算机工程与应用,2017,53(9):190-194.] [3]LIU Qingmin,ZHANG Lei,LI Xue.Improved Canny image edge detection algorithm for chip image[J].Computer Engineering and Design,2016,37(11):3063-3067(in Chinese).[刘庆民,张蕾,李雪.基于改进Canny的芯片图像边缘检测算法[J].计算机工程与设计,2016,37(11):3063-3067.] [4]WU Xiang,YU Wubo,MA Yanhui,et al.New modified Canny image edge detection algorithm[J].Journal of Image Science and Photochemistry,2016,34(1):116-121(in Chinese).[吴翔,于微波,马艳辉,等.一种新的改进Canny图像边缘检测算法[J].影像科学与光化学,2016,34(1):116-121.] [5]Chen X F,Guan H B,Gu J N,et al.A study and improvements on Canny algorithm[J].Advanced Engineering Forum,2012,6(9):205-209. [6]XU Xinchao,FU Chen,XU Aigong.Improved Canny edge extraction method[J].Remote Sensing Information,2016,31(5):43-46(in Chinese).[徐辛超,付晨,徐爱功.一种改进的Canny边缘提取方法[J].遥感信息,2016,31(5):43-46.] [7]XU Hongke,QIN Yanyan,CHEN Huiru.A edge detection algorithm based on improved Canny[J].Infrared Technology,2014,36(3):210-214(in Chinese).[许宏科,秦严严,陈会茹.一种基于改进Canny的边缘检测算法[J].红外技术,2014,36(3):210-214.] [8]Zhang Xianhong,Zhang Chunrui.Canny optimization algorithm based on improved anisotropic diffusion function filtering[J].International Journal of Signal Processing,Image Proces-sing and Pattern Recognition,2016,9(7):1-12. [9]Tao Sun,Chang Zhigao.An improved canny edge detection algorithm[J].Applied Mechanics and Materials,2013,291(2):2869-2873. [10]ZHANG Yujing,WANG Daquan,MA Yanhui.An improved adaptive median filter algorithm study[J].Industrial Control Computer,2016,29(11):109-110(in Chinese).[张玉静,王大全,马艳辉.一种改进的自适应中值滤波算法研究[J].工业控制计算机,2016,29(11):109-110.] [11]PAN Tao,WU Xiaobo,ZHANG Weiwei,et al.Application of improved adaptive median filtering algorithm in image denoising[J].Journal of Logistics Engineering,2015,31(5):92-96(in Chinese).[潘涛,吴晓波,张伟伟,等.改进自适应中值滤波算法在图像去噪中的应用[J].后勤工程学院学报,2015,31(5):92-96.] [12]DING Xiaofeng,HE Kailin.An improved image segmentation algorithm based on the variance of the most common types[J].Computer Engineering and Design,2015,36(10):2765-2768(in Chinese).[丁晓峰,何凯霖.基于最大类间方差的改进图像分割算法[J].计算机工程与设计,2015,36(10):2765-2768.] [13]SUN Zhipeng,SHAO Xianhe,WANG Zhu,et al.The improved adaptive edge detection algorithm[J].Electrical Measurement and Instrumentation,2016,53(6):17-21(in Chinese).[孙智鹏,邵仙鹤,王翥,等.改进的自适应Canny边缘检测算法[J].电测与仪表,2016,53(6):17-21.] [14]ZHU Xingyu,DU Jinglin.Average dichotomy block sort of tetragonal tree graph layout algorithm[J].Journal of Computer-Aided Design and Graphics,2015,27(8):1451-1459(in Chinese).[朱兴宇,杜景林.均值二分法分块排序的正方化树图布局算法[J].计算机辅助设计与图形学学报,2015,27(8):1451-1459.]2.2 改进的梯度幅值和梯度角度计算方法
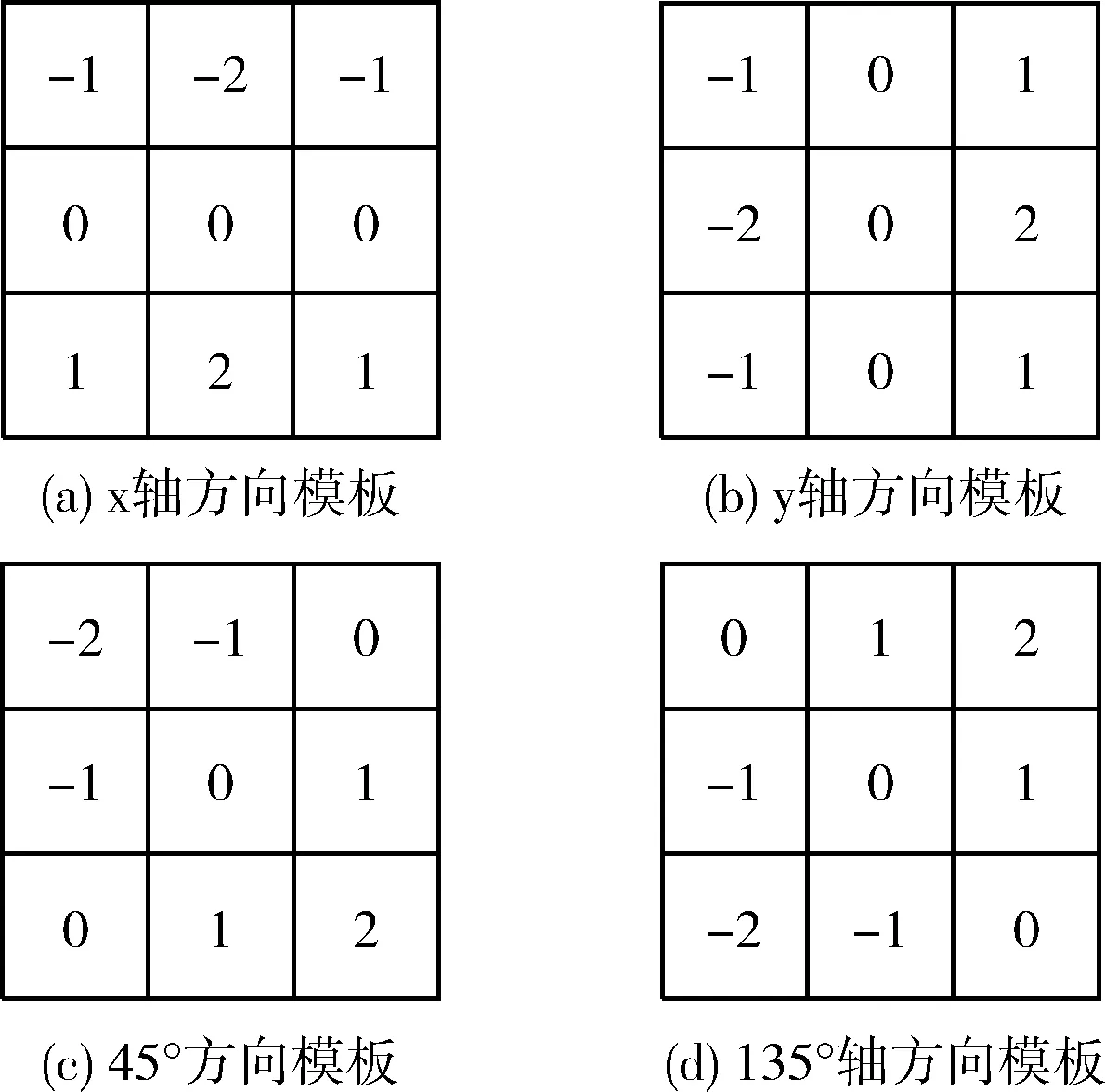
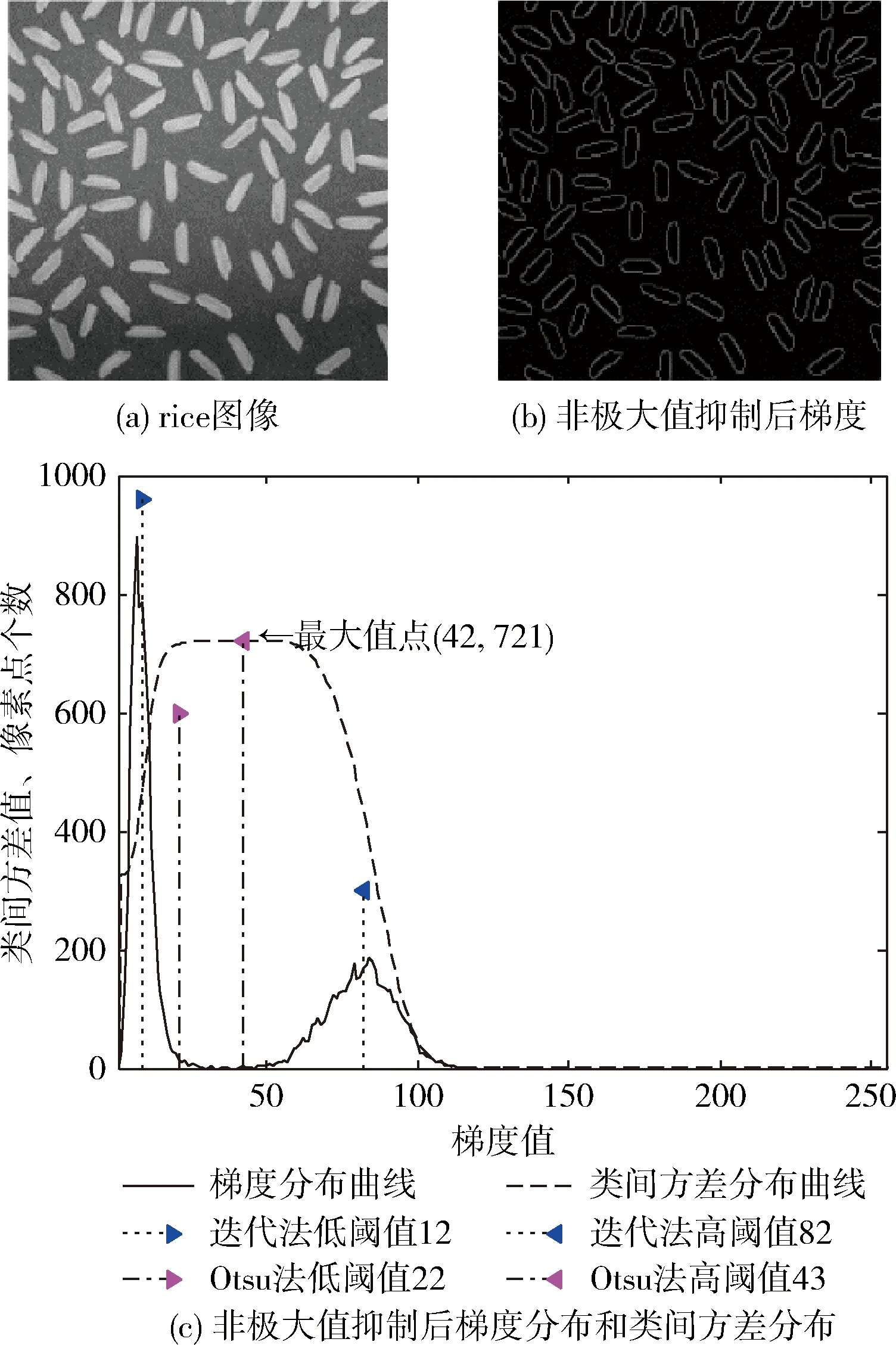
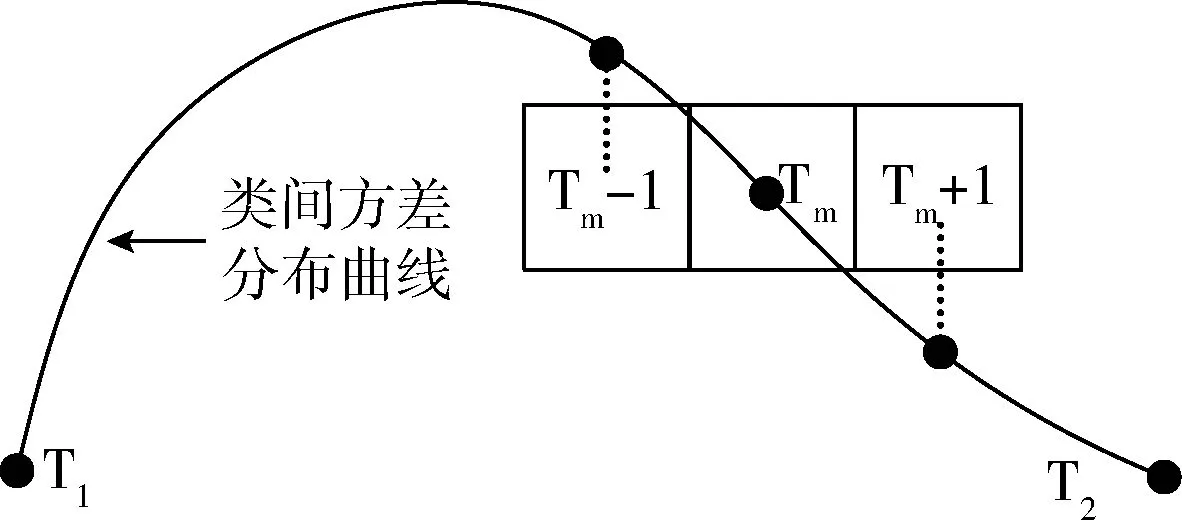
2.3 改进Otsu算法求取阈值
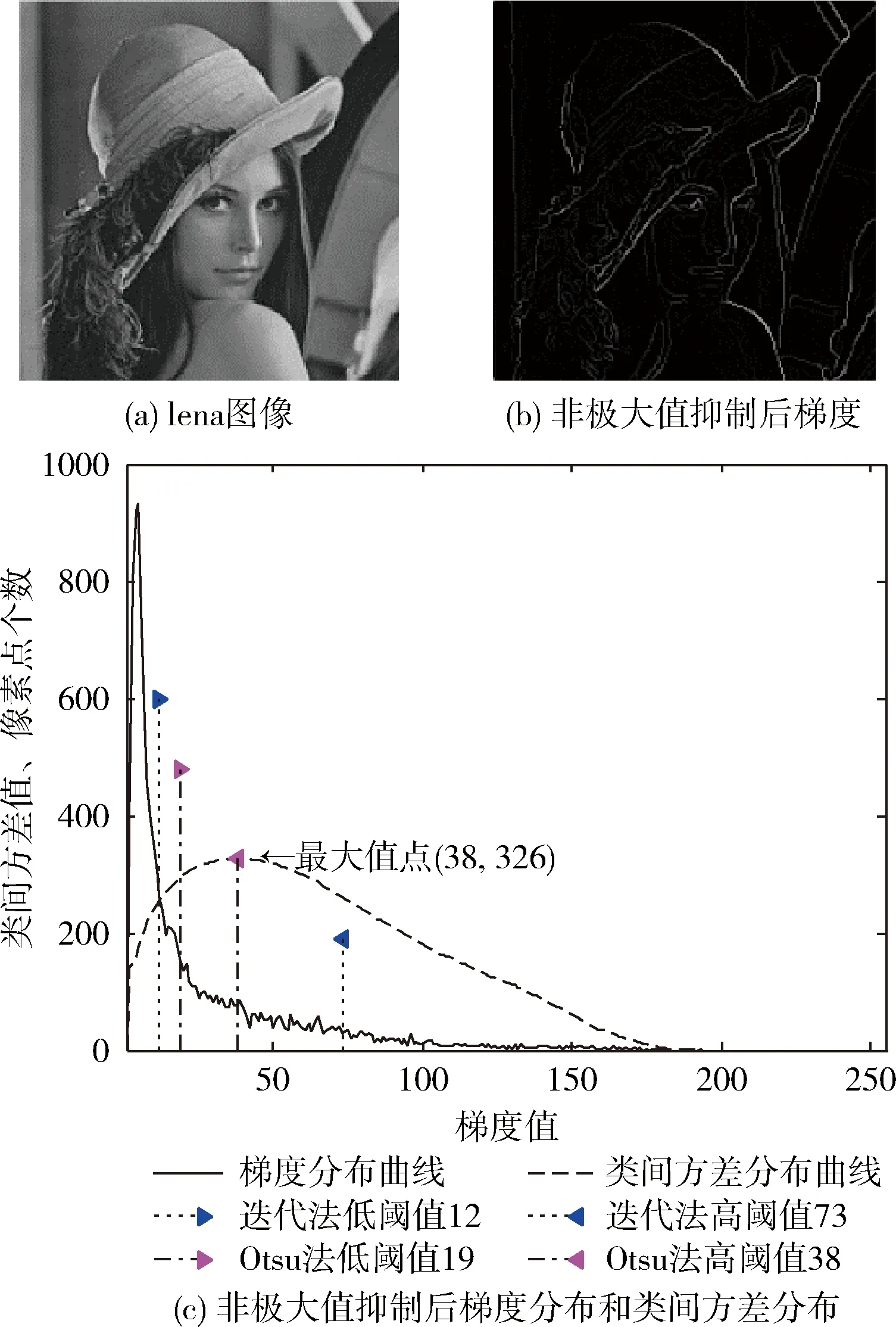
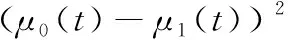
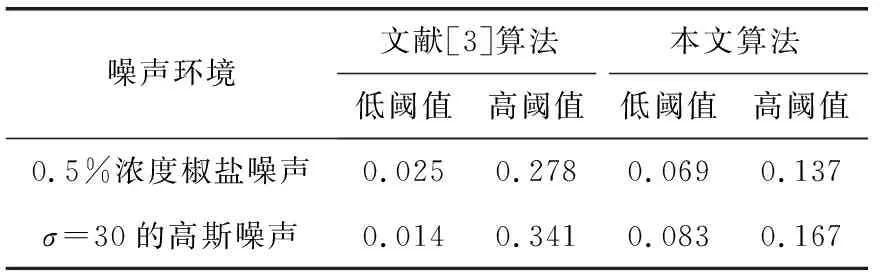
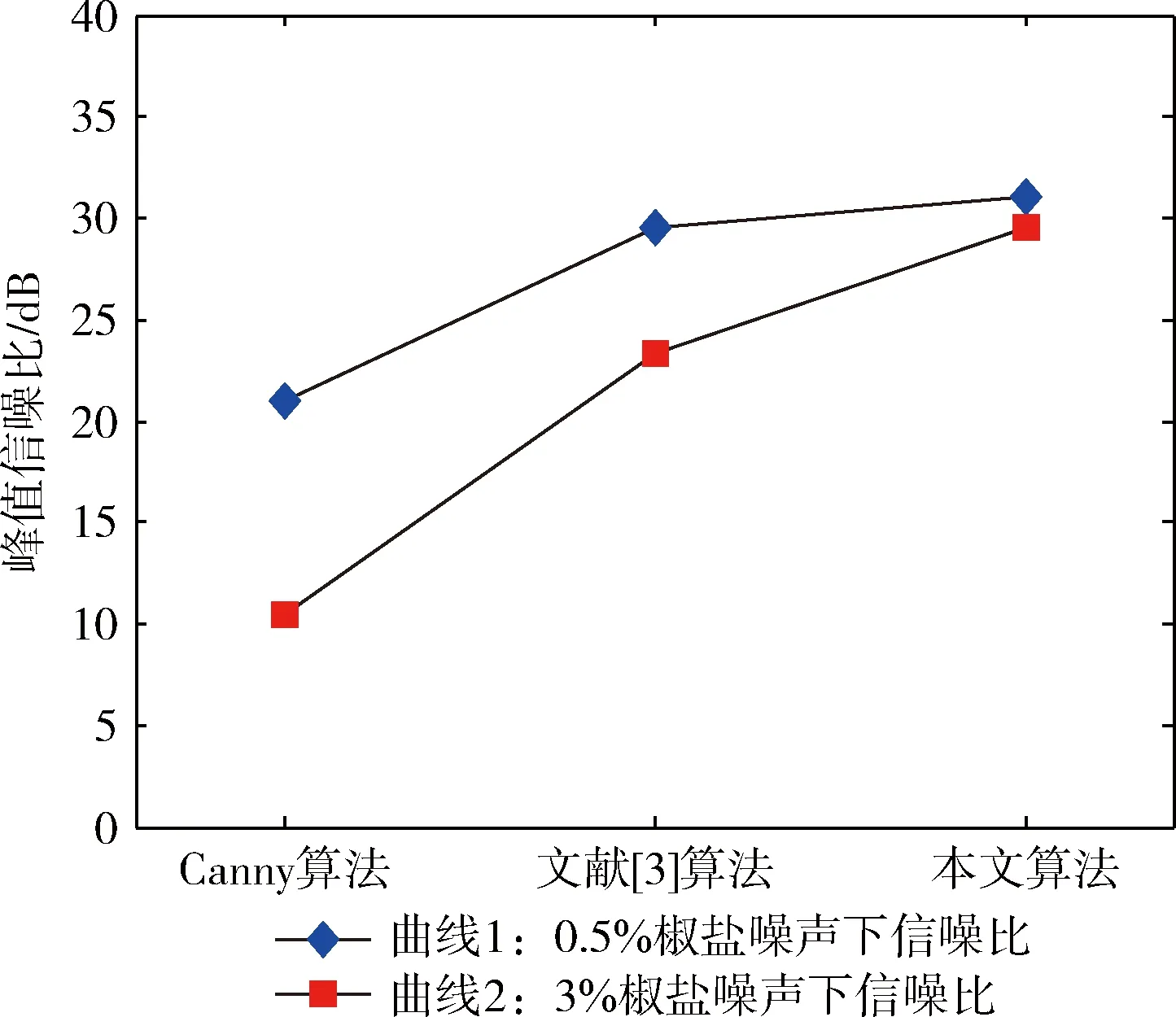
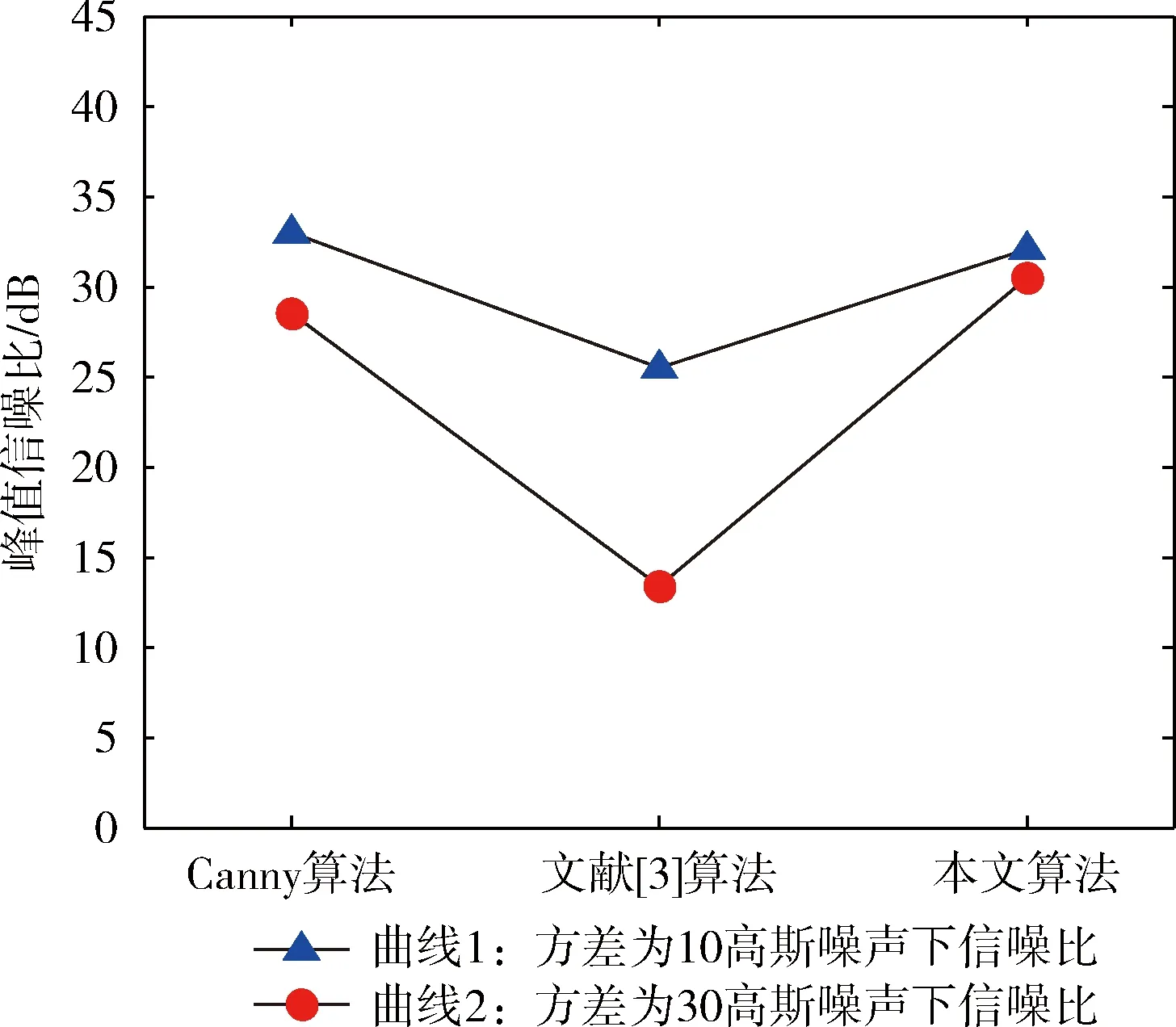
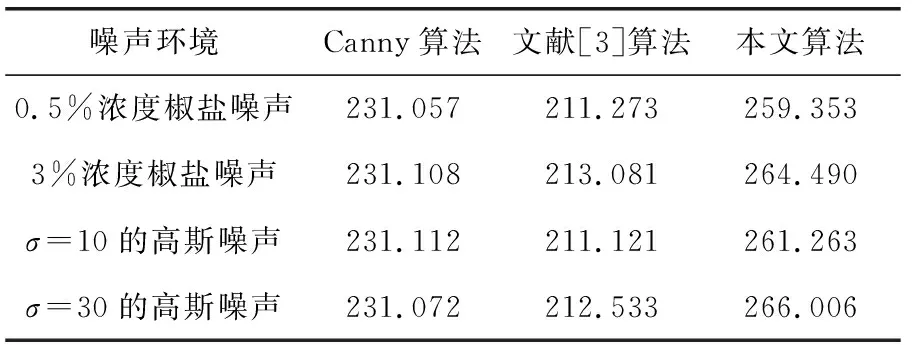
3 实验及结果分析


4 结束语
