非二进制SAR ADC的电容失配校正方法
2018-06-19陈晓青
陈晓青,叶 凡
(复旦大学 专用集成电路与系统国家重点实验室,上海 201203)
0 引 言
电荷重构型SAR ADC(successive approximation register analog-to-digital converters)因其功率和面积上的优势,是目前模数转换器的主流结构。电容型架构的DAC主要的问题是分辨率提高带来的面积开销过大问题,因此本文采用分段电容阵列DAC。又为了降低高分辨率SAR ADC对电容失配的要求,采用了整数权重的冗余结构,降低高分辨率SAR ADC对电容失配的要求的同时,也为校正提供了基础。校正算法采用目前广泛采用的LMS算法,为了避免使用额外的参考ADC而带来的面积和功耗开销,设计了采用DEM技术的准随机电容阵列。MATLAB中的仿真结果表明了本设计良好的校正效果,INL性能得到改善,分辨率提高至12 bit,动态性能也大幅度提升。
1 分段电容式SAR ADC及其电容失配分析
电荷重构型逐次逼近ADC凭借低功耗,模拟功能模块小,以及有利于缩小尺寸等特点得到快速发展[1]。由于逐次逼近型模数转换器不需要运算放大器,使得逐次逼近型ADC相比于其它架构的ADC更适合现代互补金属氧化物半导体(complementary metal oxide semiconductors,CMOS)的工艺演进路线[2]。此外,SAR ADC还具有结构简单、功耗低、面积小、易集成等特点,因此越来越成为学者的研究重点,多用于中高精度的应用中[3,4]。
1.1 二进制权重电容阵列SAR ADC
传统的逐次逼近型ADC一般采用的是二进制电容阵列来实现模数转换。最高位权重电容的容值与最低位电容容值之比为2N-1,随N呈指数增加,会增大芯片的面积,降低转换速度。为了减小芯片面积,10-12比特的应用中多采用由单位电容组成的分段式二进制权重电容阵列的DAC。大致上,分段式SAR ADC包含两个电容阵列,用一个桥接电容连接。为了能使得两个阵列匹配,LSB阵列的总电容要等于MSB阵列的最低权重电容。这要求桥接电容是一个分数电容,这很难匹配也很难设计实现。因此,ADC的线性度会严重下降[5]。
传统的分段电容阵列SAR ADC一般由两个子二进制电容阵列:LSB阵列和MSB阵列,一个采样保持器(S & H),一个比较器,和一个逐次逼近控制模块组成。图1是一个N位的带有桥接结构的SAR ADC示意图,该ADC的LSB阵列和MSB阵列分别由l个和m个权重电容组成,l+m=N。
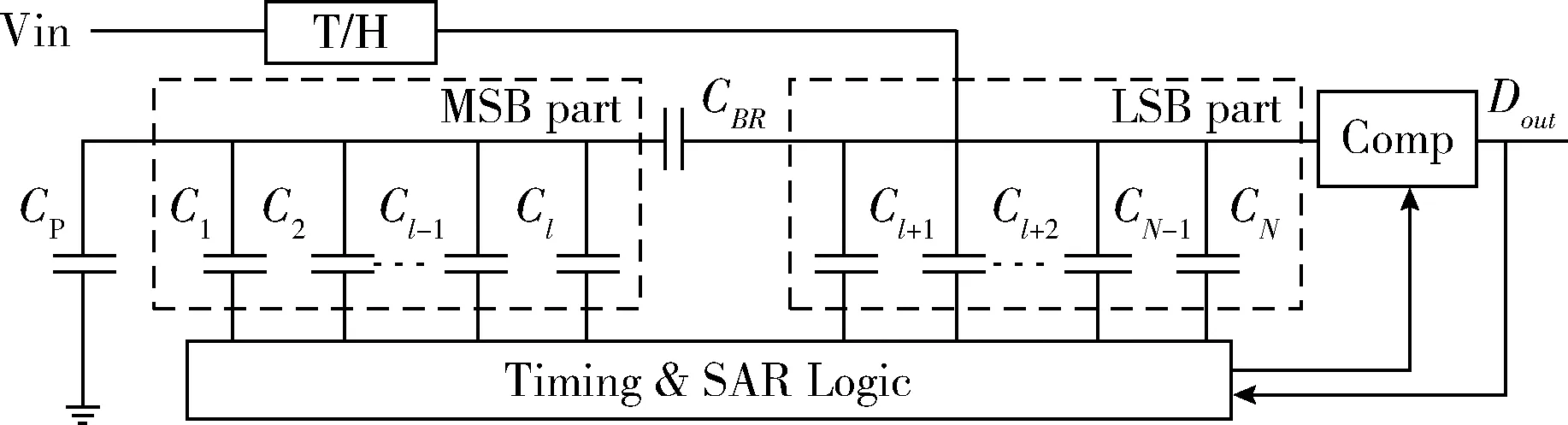
图1 桥接结构电容阵列式SAR ADC
如图1所示,低位LSB部分有l个权重电容:Cl~C1,高位MSB部分有m=N-l个权重电容:Cl+1~CN,两个子电容阵列通过桥接电容CBR连接,CP为LSB阵列的上极板节点到地的寄生电容。由于桥接电容CBR的存在,LSB阵列中各电容Ci的等效权重,等于其设计权重(也就是该电容Ci与最小电容C1之比,即Wi=Ci/C1)除以权重调整系数FW,或者说MSB阵列中各电容Ci的等效权重,等于其设计权重(也就是该电容Ci与最小电容C1之比,即Wi=Ci/C1)乘上权重调整系数FW
(1)
正是由于桥接电容CBR的引入,使得MSB阵列的权重电容容值可以缩减一个系数FW,很大程度上减小了面积开销。然而,分段电容结构的共有问题是寄生电容以及分数桥接电容的失配引起的误差,导致精确度下降[6]。
然而,当电容存在失配问题时,桥接结构会恶化模数转换器的线性度性能,有效位数ENOB被限制在10比特以下。实际上,每增加5%的电容失配,模数转换器的信噪比SNDR会下降3 dB[7]。
1.2 SAR ADC电容失配分析
目前的SAR ADC测试出来精度不高,主要可以归咎于两点:寄生误差和失配误差。在集成电路加工制造时,由于工艺波动等因素,会造成器件的随机失配。如果没有校准,逐次逼近型模数转换器能够得到的最大精度是12位。对于12位以上的精度,需要校准技术来降低电容失配的影响。CMOS器件尺寸按比例缩小使得数字校准方法具有很大的优势。
一个N比特分辨率的分段式电容阵列SAR ADC,LSB部分由l个权重电容组成,MSB由m(N-l)个权重电容组成,理想情况下,各权重电容Ci之间的关系符合下式
(2)
其中,C0是理想的单位电容,LSB阵列和MSB阵列的各个电容都有由整数个单位电容组成的。实际情况中,由于工艺波动等因素,单位电容C0符合均值为1,标准差为σu的高斯分布[3]。由单位电容C0组成的各个权重电容的实际值Ci_act也会偏离理想的电容值Ci。根据
(3)
σi是第i个权重电容的失配方差,从上式可以看出来,电容越大,则相应的失配越小,因此12比特以下的SAR ADC可以通过采用大电容来降低电容失配。
等效的权重Wi是权重电容的电容值和单位电容的电容值之比,也就是
(4)
如果电容失配存在的情况下,那么实际的权重会偏离设计权重,导致相邻两个电容的权重之比不等于设计值2,实际的权重用下式计算
(5)
上式等号右边分为两个部分,第一项是理想的设计权重Wi,第二项是由于电容失配导致的权重误差,这一权重误差是随机的,在加工制造之前是无法预知的。这样,正确的量化结果Dact应该用下式计算
(6)
但是由于实际的权重Wi_act无法预知,所以,在计算量化结果时,只能用设计权重Wi代替实际权重Wi_act
(7)
由于桥接电容CBR的存在,MSB阵列的等效权重相比LSB阵列会恶化的更严重,这是因为上式的权重误差部分全部都放大了一个权重调整系数FW。MSB阵列各权重电容的实际等效权重用下式计算
(8)
图2给出了传统二进制权重SAR ADC和采用桥接结构的二进制权重SAR ADC的INL性能比较。
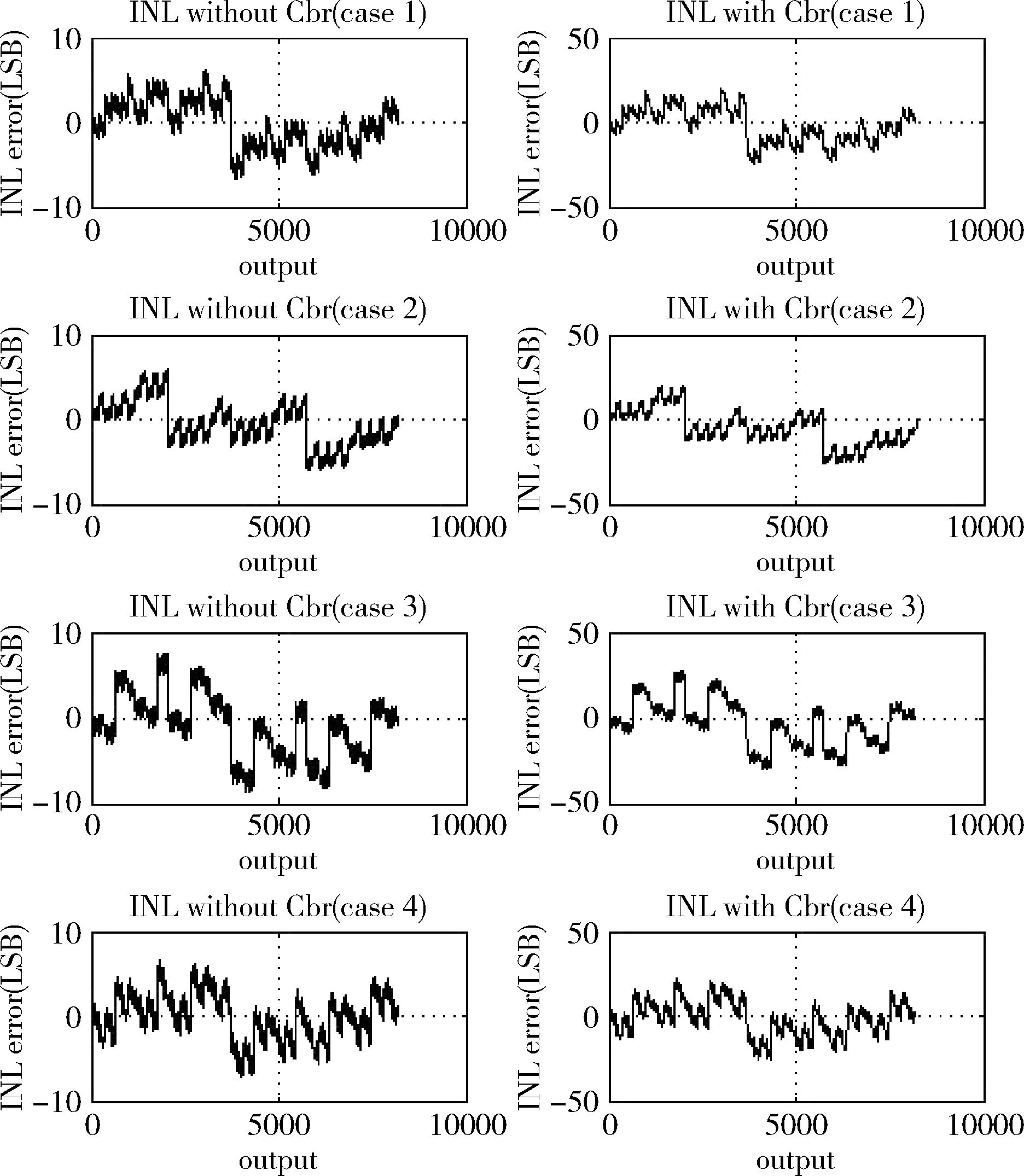
图2 桥接结构和传统电容阵列SAR ADC的INL性能比较
如图2所示,桥接电容CBR的引入会恶化由于电容失配导致的SAR ADC非线性误差,因此,高分辨率SAR ADC采用分段电容式结构来降低面积开销的前提是要消除电容失配的影响。
ADC的精确度主要取决于任意两个电容的真实的比值,最大的电容失配的允许值完全取决于精确度N。现在的技术中心,最大电容失配容许值大约在0.1%。随着分辨率的提高,要求更小的电容失配方差,意味着对于高分辨率的C-DAC而言,电容的取值和面积将急剧增加。分辨率每增加1 bit,电容匹配的方差就要降低一半,而电容取值及其面积需要增加4倍。从集成的角度考虑,12 bit以上的分辨率已经无法通过增加电容面积来满足匹配要求。这样,无法消除的电容失配,以及由此导致的Dout相对于Dact的误差,也就成为提高SAR ADC的一个根本限制因素。
2 非二进制权重的冗余结构SAR ADC
SAR ADC在原理上是通过对采样输入Vin与电容阵列C-DAC上的电压进行比较,并根据比较结果在电容阵列C-DAC建立逐渐逼近采样输入Vin的中间电压,进而得到量化结果。因此,C-DAC上电压的准确建立是SAR ADC得以进行正确量化的前提。
传统的二进制权重SAR ADC中,每一比特的量化结果都到在电压完全建立结束才可以进行比较,若逐次比较中第n次比较在电压未完全建立的情况下进行,就会导致比较结果出错,相应的电压逼近方向发生错误,由于2n>∑2i,i=(0,1,…,n-1),即使后续低位的比较结果全部正确,并使得逼近电压方向得到纠正,也无法弥补之前出错的结果,这也就意味着ADC的逐次比较没有正确完成。
为了解决这一问题,可以采用冗余非二进制权重的电容阵列[8]。非二进制权重的C-DAC之所以可以避免非线性误差是因为它允许电压的不完全建立,这样即使存在权重偏差,只要在冗余范围内,低位的量化结果也可以弥补由于高位权重误差导致的量化错误[9]。以13比特的非二进制权重SAR ADC为例,表1是其中一种权重划分的可能。
为了保证量化的线性度,要求非二进制权重的电容阵列中,任意一位电容Ci,其更低位电容的权重之和∑Cj,j=(0,1,…,i-1)≥该位电容的权重-1(Ci-1),等价于相邻的两个电容权重之比≤2,这就要求更多的比较次数,使得量化输出可以覆盖所有的输入编码。为了覆盖所有的输入编码,比较周期从13增加到了15。
1、整个更换阀门过程中滤油机、真空泵、电源箱必须设专人看守,密切关注滤油机和真空泵的运行状态,发现异常立刻向工作负责人汇报。
如果电容的权重偏差在冗余范围内,通常是20%的容错比例,即
(9)
那么,SAR ADC的量化过程仍然可以完成,得到的量化结果用下式计算
(10)
上式中,Di是每一个比较周期得到的结果,对于表1所设计的非二进制权重SAR ADC来说,需要15个周期。采用冗余结构可以使SAR ADC在各种误差存在的情况下,仍然可以正确工作并能够进行误差的提取,只要SAR ADC可以得到正确的比较结果Di,就可以为后续的权重误差提取提供比较的前提,基于此,通过后续的误差提取,获得实际权重Wi_act,就能对ADC的结果进行有效校正。
对于冗余结构的13 bit SAR ADC,采用表1的C-DAC编码,需要15个比较周期,相较于传统二进制编码增加了两次比较与C-DAC建立的时间。但是,考虑冗余结构带来的精度提升和为误差提取和校正所创造的条件,其综合收益是远远大于代价的。
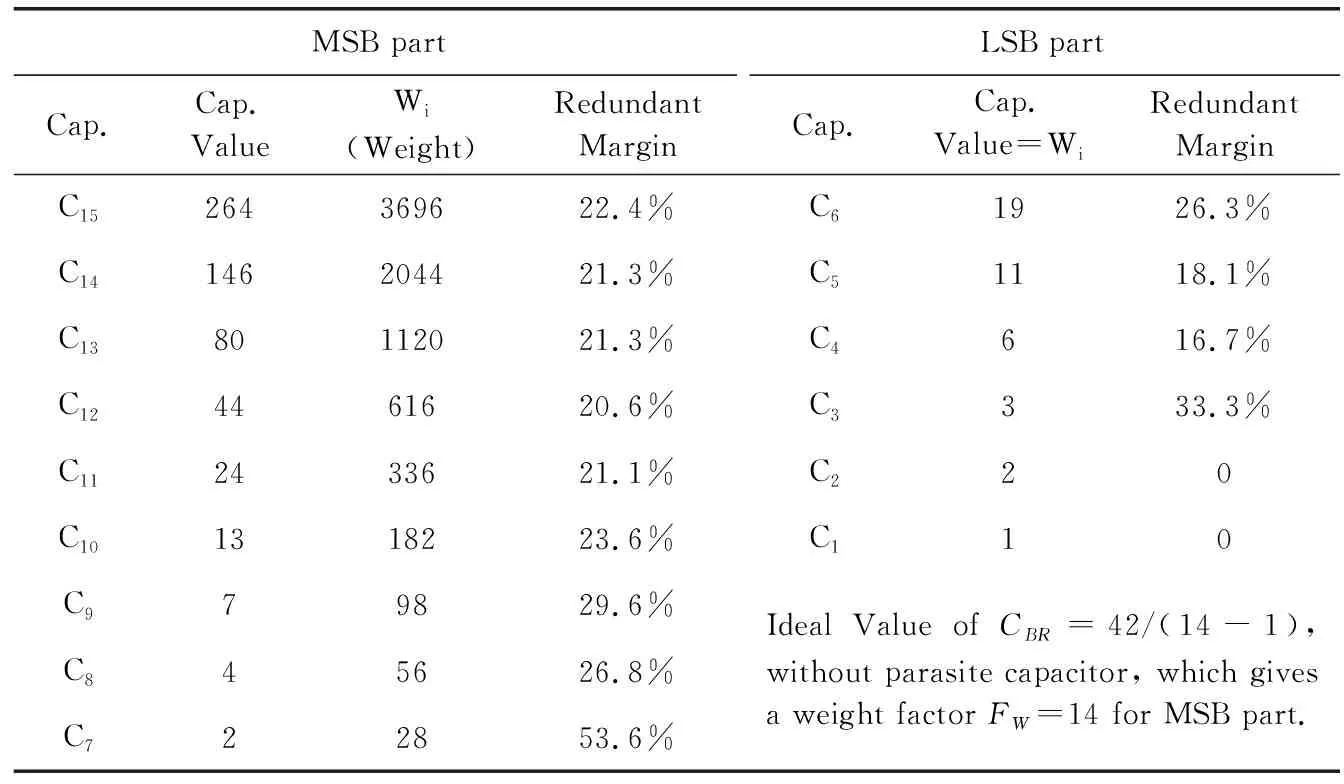
表1 13 bit桥接结构非二进制权重冗余C-DAC阵列电容设计
即使不考虑精度的收益,由于冗余编码允许20%左右的输入容错,也就是说允许DAC只建立到80%,一阶RC网络的建立误差为e-t/τ<20%即可,计算可得,一次建立用时1.6τ,15次建立只需24.0τ。
若采用无冗余设计,为满足精度要求,对于MSB要求建立误差e-t/τ<2-13,所需建立时间为9.0τ,总共建立时间为117.0τ。因此,理论上说采用冗余结构不仅不会因为比较次数增加而降低速度,反而由于允许DAC的不完全建立而能够显著缩短建立时间,提高速度[5]。
3 基于LMS的结合DEM技术的校正方法
目前对SAR ADC的校正技术主要可以分为模拟域的前台校正和数字域的后台校正两大类。对于传统的模拟域校正来说,需要一个校正DAC,电路在正常量化模式之前先进入校正模式,对所需校正的所有电容进行测量和量化,根据特定的校正算法提取所需的校正系数,并且以误差码的形式存储在寄存器中。待进入正常量化模式后,或是将存储的误差码加到量化后的输出编码中,或是通过校正DAC将误差码表示的电压加到主DAC的输出上,从而达到减小或者消除电容失配的目的,由于模拟域前台校正需经常中断正常量化模式来进行校正,效率比较低。数字域的后台校正技术优势在于可以通过校正算法实时跟踪器件参数的变化,并且不会修改模拟电路的任何参数以及不增加额外的模拟电路,使得数字后台称为近年来热门的校正技术[10]。
3.1 传统的LMS校正方案
最小均方(least mean square,LMS)算法是一种得到广泛应用的收敛算法。在校正阶段,如果ADC输入信号Vin所对应的准确数字量Dcal已知,而SAR ADC量化结果为Dout,则可以基于LMS算法对SAR过程中的各电容权重进行提取。
LMS迭代算法的具体公式如下
error(n)=Dcal(n)-Dout(n)
Wi(n+1)=Wi(n)-μ×error(n)Di(n)
(11)
Dout是基于设计权重Wi计算得到的输出,Dcal是已知的ADC输入,通过两者的误差error以及对应各权重的Di对相应权重进行修正,通过反复多次的迭代,最终权重会从初始值,即设计权重Wi,收敛到实际值Wi_act。图3为传统的采用LMS算法校正的SAR ADC结构图。

图3 传统带参考DAC的LMS校正方案
上述传统的LMS算法需要已知的ADC输入Vin或者量化结果Dcal,传统的做法是采用参考ADC或者参考DAC实现。但是,参考ADC增加了额外的面积开销,复杂度也提高了。因此,本文提出了C-DAC复用的方法。
3.2 结合pure-DEM技术的LMS校正方案
对于电容阵列结构的SAR ADC而言,其本身自带了由各权重电容Ci组成的C-DAC,逐次比较的量化过程就是C-DAC反复的过程。因此,如果在采样阶段,对C-DAC施加参考数字信号Dcal,产生参考输入电压Vref,就不需要增加额外的参考DAC了。此时,SAR ADC有两个模式:校正模式和正常工作模式。在校正模式下,首先由外部数字信号Dcal通过C-DAC产生参考电压Vref,随后SAR ADC对产生的参考电压Vref进行量化,并通过LMS算法对误差进行校正,待LMS算法收敛,权重误差提取完成后,进入正常工作模式,外部输入Vin通过逐次比较,得到数字输出Di,再由正确的权重加权求和得到校正后的结果Dact。
然而,直接对C-DAC中的15个权重电容施加15 bit的Dcal来产生参考输入,对误差提取是无效的。这一做法相当于用带误差的信号源校正自身的误差,无论权重误差是否存在,在采样阶段用C-DAC阵列直接产生的参考输入,并在逐次比较阶段用同样的C-DAC进行量化,两者之间不会存在不一致,也就提取不出误差,LMS算法无法进行。
本文结合动态元件匹配(dynamic element matching,DEM)技术的C-DAC复用方法。在采样阶段,基于DEM思想,将元件单元完全打散,也就是说,在此阶段,把C-DAC中各权重电容都分拆成最基本的单元电容,根据表1,MSB部分有584个单元电容,LSB部分有42个单元电容,若能够通过外部产生的相互独立的626个随机的比特“0”或“1”控制每个单元电容,则产生的整体输出电压由各个单元电容的实际值和控制比特决定。虽然单次结果取决于实际为1的各单元电容容值,但根据概率理论,其平均值与单个电容的具体值无关。因此,从大量结果的平均效果看,DEM后的C-DAC可以看作一个近似理想的DAC,这正是DEM方法的核心思想。
在逐次逼近的量化阶段,再将C-DAC电容重组为符合表1的各权重电容进行逐次逼近量化,再通过逐次比较的结果,进行LMS迭代计算,即可提取SAR阶段C-DAC各权重电容组合的权重误差。
采用完全DEM校正方案的SAR ADC如图4所示。
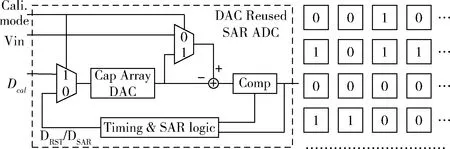
图4 采用完全DEM校正方案的SAR ADC
3.3 结合pseudo-DEM技术的LMS校正方案
上述的完全DEM(pure-DEM)方法在原理上是可行的,但是在实现上代价太大,对626个单位电容分别加以控制需要626个开关,这会大大增加电容阵列的面积和互连的复杂度,因此需要加以简化,以提高其可实现性。
为了布局布线的方便,电容阵列一般为矩形,例如对表1中的MSB阵列的584个单位电容采用8*73的阵列,每一列的8个单位电容相连,在列边界上分别连接一个开关,控制整列的所有电容,这样就把MSB阵列的584个开关缩减到73个开关。但是此方法也存在问题,当某个开关为“0”或者“1”时,这一列的所有电容都为“0”或“1”,也就是说输入信号只可能是8的倍数(0,8,8*2,…,8*72),这样产生的输入信号就失去了随机性,导致部分权重电容无法被校正。
因此,本文进一步提出准DEM(pseudo-DEM)方法,也就是将电容阵列拆成76列,每列仍然是8个单位电容,在列边界进行连接,但并不是每列作为一个电容,电容拆分仍是准随机的,只是拆分的电容都只连接到某列的边界以方便连接。将这些拆分电容作为DEM的单位电容进行随机化,用76个控制比特产生参考电压。虽然准随机电容单元远远少于完全DEM的626个电容单元,但是由于随机化,可产生的参考电压范围也足够覆盖大部分输入编码。
图5是MSB阵列中最高位权重电容C15的示意图,如表1所示,C15实际由264个单位电容组成,因此采用的是8*33的阵列。如果不采用准DEM,则此33列电容只能产生(0,8,8*2…,8*32)这些参考电压。采用准DEM以后,仍然由33个开关在列边界控制参考电压产生,区别只是8*33电容阵列之间每个电容的连接不同。本设计中此264个单位电容共组成容值为(11,10,9,8,7,6,5)的33个电容,分别是容值为11的2个,容值为10的5个,容值为9的6个,容值为8的7个,容值为7的6个,容值为6的5个,容值为5的2个,这样产生的输入信号具有一定随机性,可以覆盖更多的输入编码。其余的各权重电容也按照相似的随机化进行划分和连接,虽然少于pure-DEM的626个单位电容,但是其数量远远大于确定型电容阵列的76个权重电容。
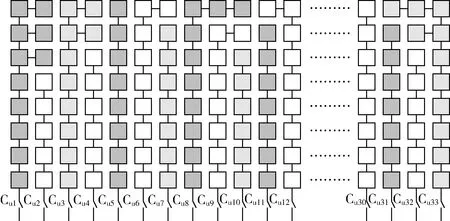
图5 准随机权重DAC中MSB电容阵列的电容划分
4 仿真结果
本设计在MATLAB中进行系统级仿真。采用pseudo-DEM技术的LMS校正SAR ADC整体结构如图6所示。其中电容阵列采用表1的设计,本设计中的SAR ADC的工作分为两种模式:校正模式和正常量化模式。电容失配设为当前工艺技术能实现的0.1%,分别在没有校正,采用pure-DEM方案校正和pseudo-DEM方案的情况下对13 bit SAR ADC进行了仿真。比较未采用校正方案、采用pure-DEM方案、采用pseudo-DEM方案后,SAR ADC的INL性能。
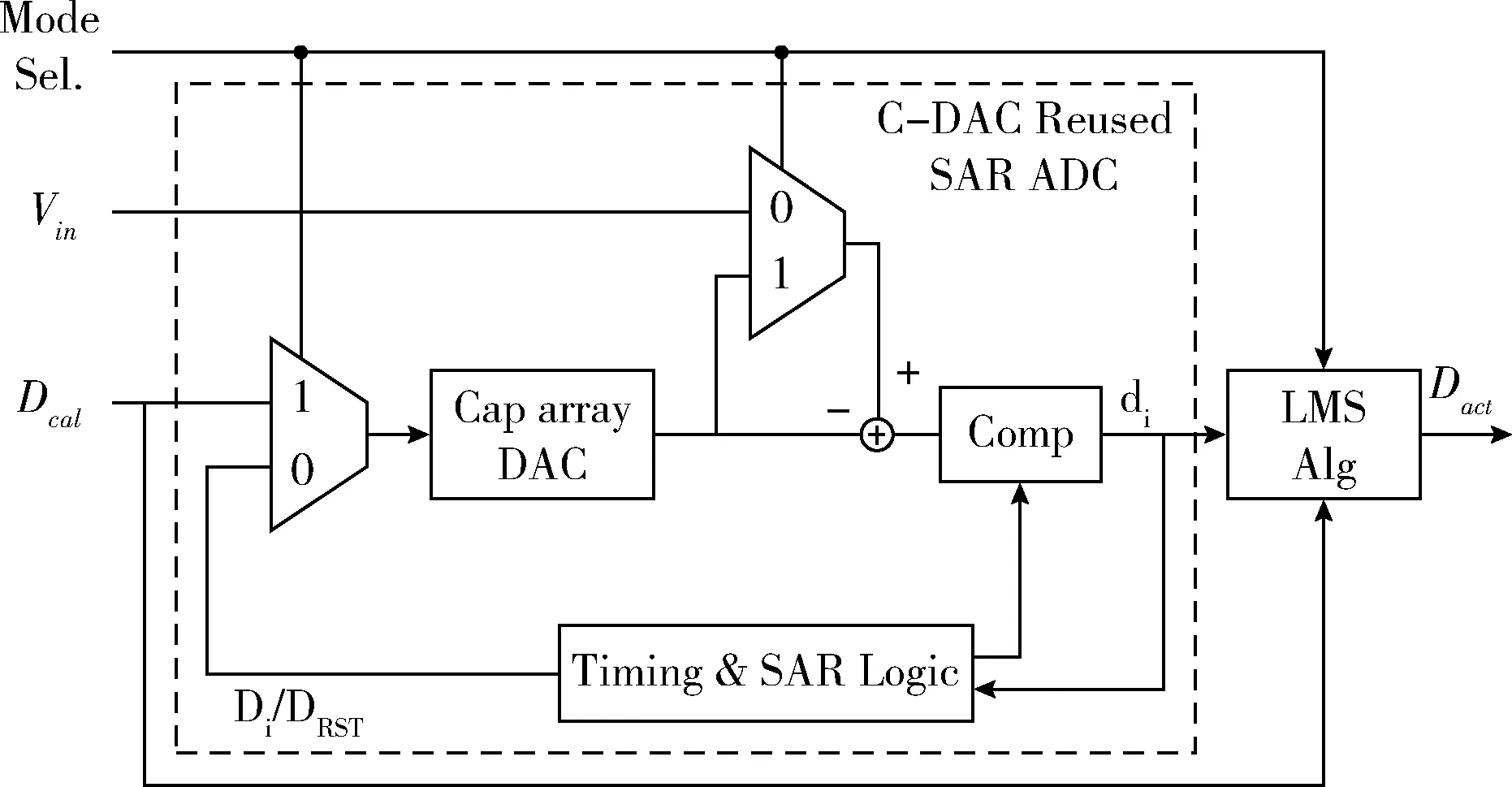
图6 结合pseudo-DEM的LMS校正SAR ADC整体结构
图7所示的是,同一标准差下(σu=0.1%)产生随机的4组电容失配,比较未矫正前、采用pure-DEM方案、采用pseudo-DEM方案校正后的权重误差(Ci-Ci_act)/C0。

图7 校正前后的权重失配比较
如图7所示,未矫正前,实际权重Wi_act偏离设计权重Wi很多,采用pure-DEM和pseudo-DEM校正后,获得的校正权重Wi-cal很大程度上向实际权重Wi_act趋近,因此可以用校正权重Wi-cal替代设计权重Wi来计算量化结果,从而可以在实际权重Wi_act无法获得的情况下,也可以得到较为准确的量化结果,改善SAR ADC的非线性问题。
图8是未校正前、采用pure-DEM校正后、采用pseudo-DEM矫正后的INL比较图。如图7所示,未校正前,由于电容失配,SAR ADC的INL性能恶化到±30 LSB,采用pure-DEM校正方案和采用pseudo-DEM校正方案后,INL性能分别可以达到-1.29/+1.52 LSB和-1.36/+1.26 LSB。仿真结果显示,pure-DEM校正方案和pseudo-DEM校正方案可以达到相近的优化效果,而且pseudo-DEM方案相比pure-DEM方案很大程度上降低了面积开销和互连的复杂度。因此,pseudo-DEM校正方案可以很好的消除电容失配引入的误差,而不过多的增加面积和功耗开销,同时冗余结构的设计还可以提高转换速率。
图9是未校正和采用pseudo-DEM校正方案的动态性能比较。如图所示,校正前后的SFDR性能分别测得57.1 dB和87.1 dB,SNR性能分别测得56.58 dB和78.92 dB,ENOB性能分别测得7.95 bits和12.0 bits。表2总结了本文设计的方案和已有方案之间的性能比较。
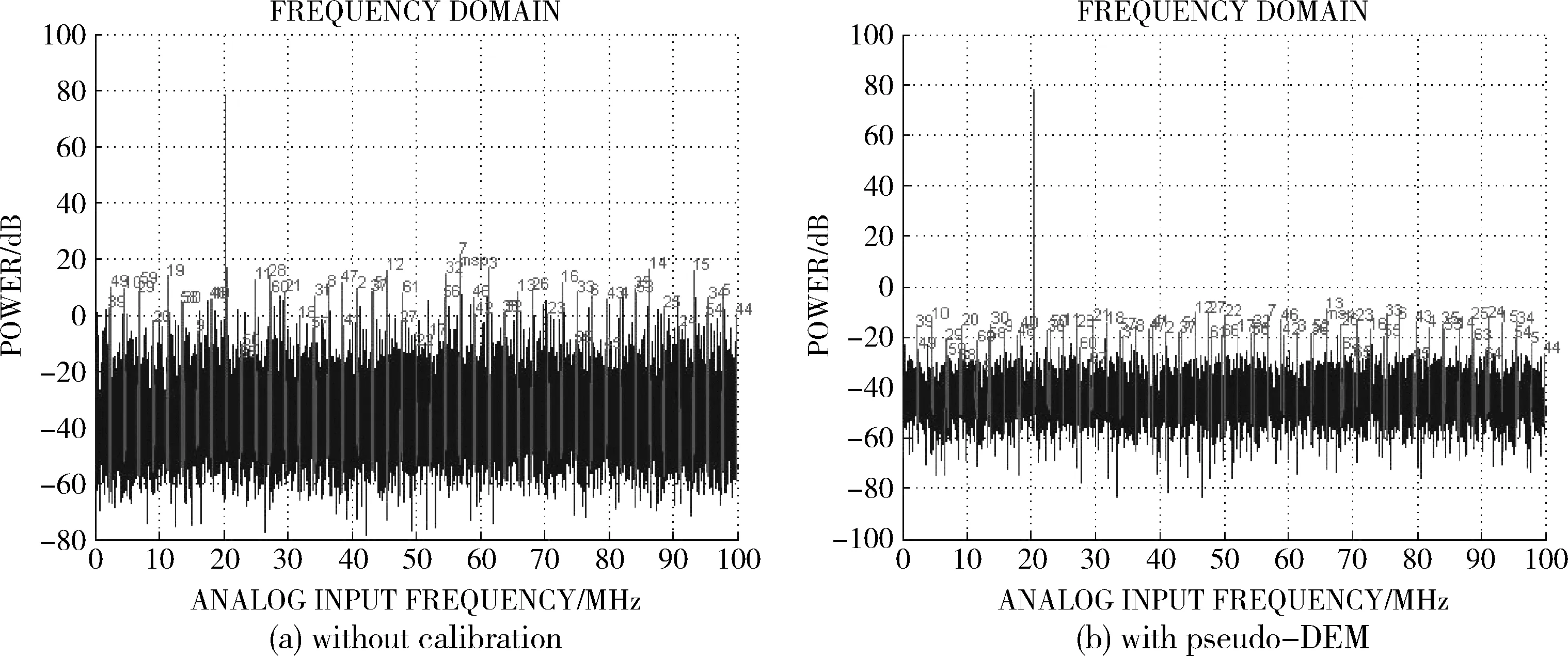
图9 校正前后的动态性能比较

Ref[2]Ref[9]This work(sim)Resolution/bit101013Sampling Rate/(MS/s)80320200INL(LSB)1.65/0.74-0.43/+0.28-1.36/+1.26SFDR/dB-74.881.6SNR5856.7987.1ENOB/bit9.6-12.0
5 结束语
SAR ADC的电容阵列失配问题会引起实际权重偏离设计权重,导致SAR ADC的线性度恶化。本文采用了冗余的非二进制权重结构和基于LMS算法,并结合伪随机动态DAC复用技术的校正方案来消除电容失配的影响。仿真结果显示,通过结合pseudo-DEM技术的LMS算法的校正以后,13比特SAR ADC可以获得良好的INL性能,ENOB也可达到12.0比特。
参考文献:
[1]Li Zhe,Lu Yuxiao,Mo Tingting.Calibration for split capacitor DAC in SAR ADC[C]//IEEE 10th International Confe-rence on ASIC(ASICON).Shenzhen:IEEE,2013:1-4.
[2]Lin YZ,Liu CC,Huang GY,et al.A 9-bit 150-MS/s subrange ADC based on SAR architecture in 90-nm CMOS[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2013,60(3):570-581.
[3]Juan-Carlos Pena-Ramos,Marian Verhelst.Split-delta back-ground calibration for SAR ADCs[J].IEEE Transactions on circuits and systems—II: Express Briefs,IEEE,2017,64(2):221-225.
[4]Choi Yongsuk,Kim Yong-Bin,Jung In-Seok.A 100MS/s 10-bit split-SAR ADC with capacitor mismatch compensation using built-in calibration[C]//IEEE 25th North Atlantic Test Workshop.Providence:IEEE,2016:1-5.
[5]Albert H Chang,Lee Hae-Seung,Duane Boning.A 12b 50 MS/s 2.1mW SAR ADC with redundancy and digital background calibration[C]//Proceedings of the ESSCIRC.Bucharest:IEEE,2013:109-112.
[6]Chen Huabin,Xiang Jixuan,Chen Chixiao,et al.A foreground digital calibration by switching control scheme for A 12-bit SAR ADC[C]//12th IEEE International Conference on Solid-State and Integrated Circuit Technology.Guilin:IEEE,2014:1-3.
[7]Anh Trong Huynh,Hoa Thai Duong,Hoang Viet Le,et al.Design of a capacitive DAC mismatch calibrator for split SAR ADC in 65 nm CMOS[C]//Asia-Pacific Microwave Confe-rence Proceedings.IEEE,2013:503-505.
[8]Liu C-C,Kuo C-H,Lin Y-Z.A 10 bit 320 MS/s Low-Cost SAR ADC for IEEE 802.11ac applications in 20nm CMOS[J].Solid-State Circuits,IEEE,2015,50(11):2645-2654.
[9]Liu Wenbo,Huang Pingli,Chiu Yun.A 12-bit 45-MS/s 3-mW redundant successive approximation register analog-to-digi-tal converter with digital calibration[J].IEEE Journal of So-lid-State Circuits,2011,46(11):2661-2672.
[10]Xu R,Liu B,Yuan J.Digitally calibrated 768-kS/s 10-b minimum-size SAR ADC array with dithering[J].Solid-State Circuits,IEEE,2012,47(9):2129-2140.
