改进叠加原理求解低渗储层关井阶段压力响应

李友全 黄春霞 王佳 于伟杰 韩凤蕊 阎燕

1. 中国石化胜利油田分公司勘探开发研究院；2. 陕西延长石油（集团）有限责任公司研究院；3. 北京金士力源科技有限公司

随着中高渗油藏逐渐进入高含水期，低渗透储层的高效开发开始在原油供给中扮演越来越重要的角色［1-5］。由于孔喉结构［6］、流体性质［7］和流固界面作用［8］的影响，流体在低渗透油藏的渗流不符合达西定律，存在非线性段［9］，是低速非达西渗流。通常用拟启动压力梯度描述低速非达西渗流，但其在关井阶段的作用机制尚不明确，使得低渗储层压力恢复测试解释结果存疑，可信度低。

压降叠加原理是求解关井阶段井底压力变化的重要方法，即关井阶段井底压力变化是真实井和虚拟井井底压力变化的叠加。对于低速非达西渗流问题，部分文献［10-11］在压降叠加时对真实井和虚拟井同时考虑了（拟）启动压力梯度的影响。计算结果显示，拟启动压力梯度使关井阶段压力-压力导数双对数曲线在后期上翘，和开井阶段影响规律类似。然而，研究人员已注意到传统压降叠加原理不能直接用于低速非达西渗流问题［12-13］。采用基于PEBI网格的算法，所得结果与传统压降叠加原理结果完全相反，即绝对启动压力梯度会使关井后压力导数曲线下掉，井底压力更早稳定。

针对数值结果和传统压降叠加原理结果的矛盾，笔者基于改进的达西定律，建立了涵盖开井和关井过程的低渗储层试井数学模型。该模型是非齐次的二阶线性微分方程组，根据其解的可叠加性，证明和提出了适用于低渗储层的改进压降叠加原理。分析了开井和关井阶段拟启动压力梯度对压力-压力导数双对数曲线的影响规律，并根据动边界理论探讨了拟启动压力梯度的两种作用机制。笔者提出的改进压降叠加原理修正了低渗储层关井阶段压力响应求解的错误，使压力恢复测试准确获取地层平均拟启动压力梯度成为可能。

1 低速非达西渗流表征

针对低速非达西渗流的非线性段，可以采用指数函数、幂函数和多参数关系式精确描述［14-16］，也可以采用拟启动压力梯度等效描述［17］。由于拟启动压力梯度方法保留了达西定律的简便性［18］，是普遍的处理方法。对应改进的达西定律如式（1）所示［16］。

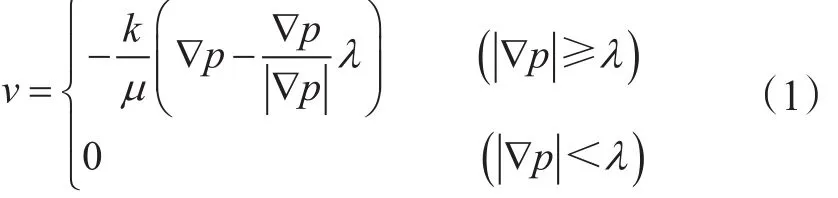
式中，ν为流动速度，cm/s；μ为流体黏度，mPa·s；k为储层有效渗透率，D； ∇p为压力梯度，10-1MPa/cm；λ是拟启动压力梯度，10-1MPa/cm。

2 改进的压降叠加原理

2.1 试井数学模型

2.1.1 基本假设 考虑一均质径向油藏，中心为一口井。具体假设为：（1）单相微可压缩液体；（2）考虑井筒储集系数C和表皮因数S的影响；（3）油井生产前，地层中各点的压力均匀分布为pi；（4）忽略重力和毛管力的影响；（5）渗流过程中存在拟启动压力梯度λ；（6）地层均质、等厚、各向同性，井以一常产量q生产；（7）地层岩石微可压缩；（8）持续开采tp时间后关井，Δt为关井时间。

2.1.2 数学模型

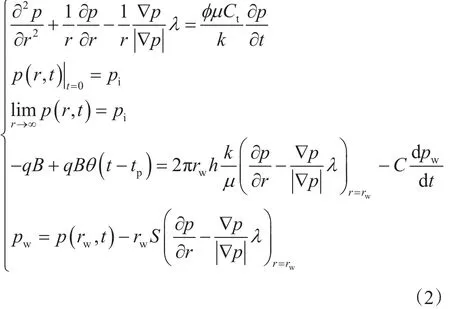
式中，r为距离，cm；φ为储层孔隙度；Ct为综合压缩系数，10 MPa-1；t为时间，s；pi为初始地层压力，10-1MPa；B为体积系数；θ为单位阶跃函数；rw为井筒半径，cm；h为储层厚度，cm；C为井筒储集系数，10 cm3/MPa；pw为井底压力，10-1MPa；S为表皮因数。

式（2）包含非齐次的虚宗量贝塞尔方程，无因次化后经过Laplace变换、Stehfest数值反演即可得到真实空间井底压力解［19-20］。

2.2 改进压降叠加原理的证明

令 Δp=pi-p=Δp1+Δp2，则方程（2）可变为

式（3）是一个线性微分方程组。根据其解的可叠加性，若Δp1满足

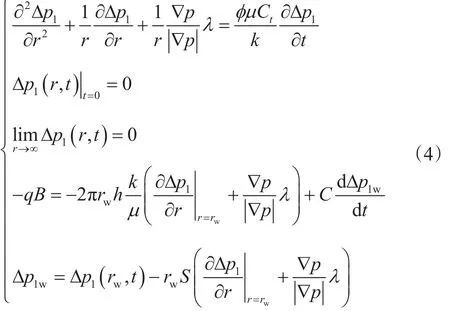
同时Δp2满足

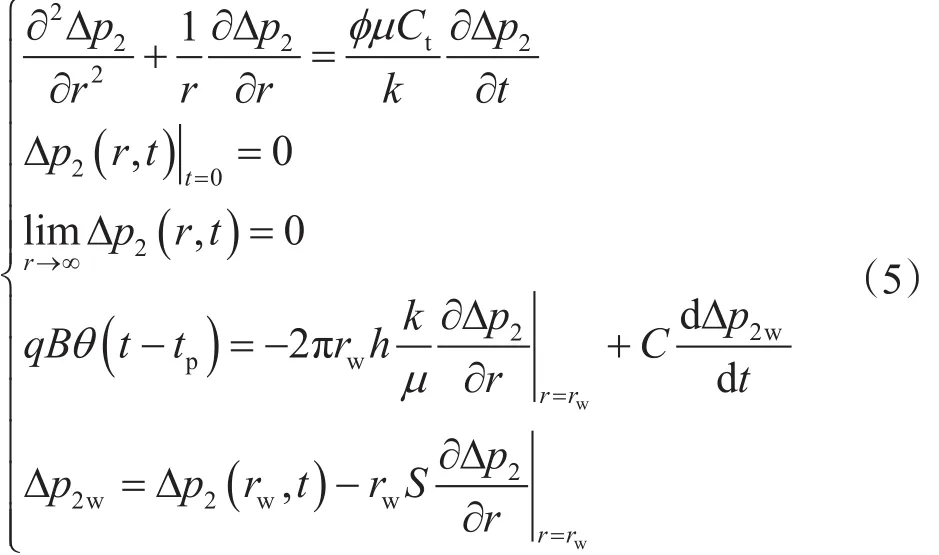
则Δp1+Δp2肯定是模型（2）的解。其中，Δp1为存在拟启动压力梯度，真实井持续生产时井底压力变化值的解；Δp2为不存在拟启动压力梯度，虚拟井从tp时投产，且产量与真实井相等时，井底压力变化值的解。因此，低渗储层关井压力恢复试井井底压力变化值（基于原始地层压力），等于一个考虑拟启动压力梯度时变化值与一个不考虑拟启动压力梯度时变化值的叠加，前期低渗储层压力恢复试井压降简单叠加的表示方法［10-11］是错误的。

从物理意义上，改进的压降叠加原理也具有其合理性。对低速非达西渗流，流体流动时拟启动压力梯度总是阻碍其流动。在关井阶段，真实地层中流体流动方向并未发生改变。因此，对于真实井，拟启动压力梯度在关井阶段存在且方向不变；对于虚拟井，真实地层中并未发生虚拟井对应的流体流动，拟启动压力梯度失去了其作用的前提条件。因此，计算关井阶段虚拟井的压力变化时不应考虑拟启动压力梯度。

3 开井过程拟启动压力梯度作用规律和机制

3.1 作用规律

应用表1参数，采用式（4）所示的持续生产时试井数学模型的井底压力变化解，计算得到不同拟启动压力梯度时压力-压力导数双对数曲线见图1。

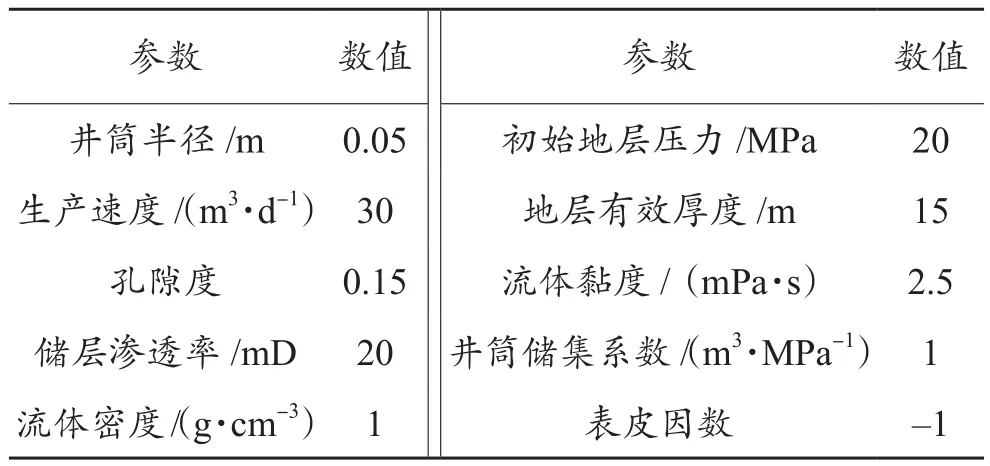
表1 压力升高/降落过程井底压力变化计算参数Table 1 Parameters for mathematical model of switch-on process

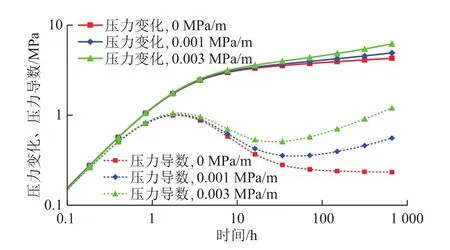
图1 压力升高/降落过程中不同拟启动压力梯度时压力-压力导数双对数曲线Fig. 1 BHP change versus time at different pseudo TPG in log-log plot

由图1可看出，对于开井生产的压力升高/降落过程，随着拟启动压力梯度从0 MPa/m升至0.01 MPa/m，压力-压力导数曲线在10 h后由趋向水平变为“上翘”，且拟启动压力梯度越大，上翘时间越早，上翘幅度越大，显示拟启动压力梯度的存在使得压力升高/降落的速度在后期不断增大，阻碍了压力的传播。

3.2 作用机制

“动边界理论”［21-22］可以用来解释拟启动压力梯度在开井过程的作用机制。对于径向均质油藏，流体速度在井点处最高，且向远井方向连续递减。根据式（1），压力梯度和流体速度具有相同的分布规律。由拟启动压力梯度的定义可知，压力梯度小于拟启动压力梯度时流体速度为0，即在远井方向拟启动压力梯度会使得某处以外区域的流体无法流动，这意味着拟启动压力梯度的作用与“封闭”边界类似。而且，在相同条件下，更大的拟启动压力梯度会使该封闭边界距井更近。在压力响应上体现为压力-压力导数曲线更早上翘，上翘幅度更大［23］。

4 关井过程拟启动压力梯度作用规律和机制

4.1 作用规律

式（3）是持续生产tp时间后关井Δp时间的试井数学模型。根据改进的压降叠加原理，tp～tp+Δp关井阶段的井底压力解是式（4）、式（5）对应井底压力变化的叠加。采用同样的计算参数（表1），取tp=100 d，则计算得到不同拟启动压力梯度时压力-压力导数双对数曲线如图2所示。

由图2可看出，对于关井的压力恢复过程，随着拟启动压力梯度从0 MPa/m升至0.01 MPa/m，压力导数曲线在30 h后由趋向水平变为“下掉”，且拟启动压力梯度越大，下掉时间越早，下掉幅度越大，显示拟启动压力梯度的存在使得压力恢复的速度在后期不断减小，地层更快到达（拟）稳态流动。图2显示的规律和数值方法计算得到的规律［12］相同，证明了改进的压降叠加原理的正确性。

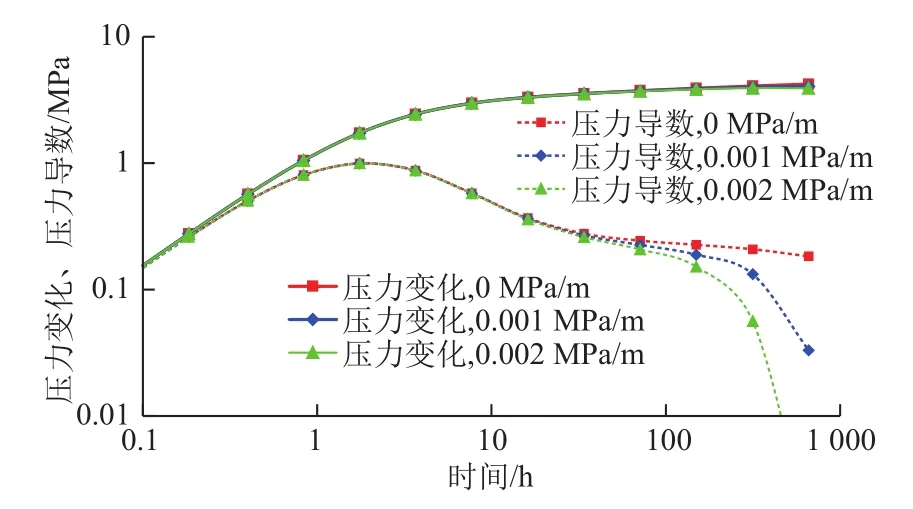
图2 压力恢复过程中不同拟启动压力梯度时压力-压力导数双对数曲线Fig. 2 BHP change versus time at different pseudo TPG in log-log plot

采用文献［12］中图5b对应参数取值，流体黏度取2 mPa·s，计算得到外边界为无限大均质油藏、拟启动压力梯度为0.05 MPa/m时对应的压力-压力导数双对数曲线（图3），可以看出压力导数曲线快速下垂，和文献中图5b特征符合，部分验证了本文提出的改进压降叠加原理正确性。

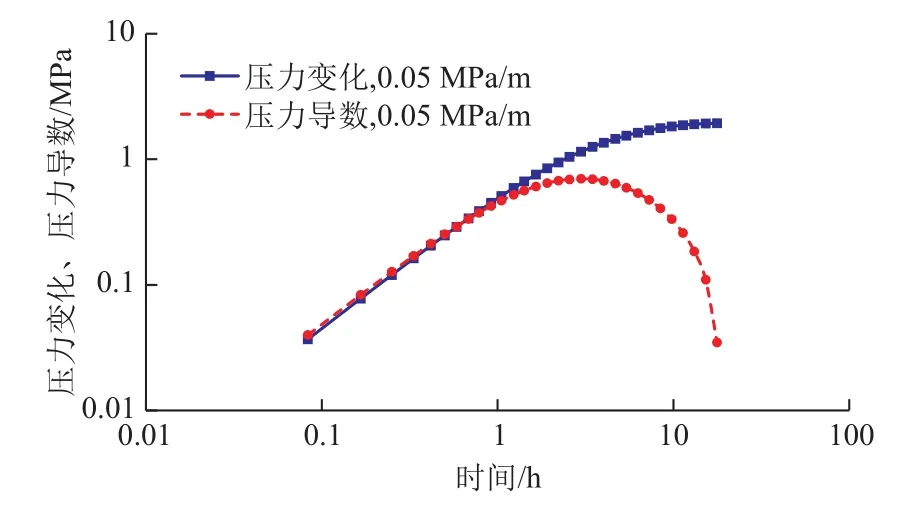
图3 采用文献［12］中图5b参数计算得到的压力-压力导数双对数曲线Fig. 3 BHP change versus time in log-log plot bу parameters from literature 12

低渗透油藏压力恢复阶段试井曲线大多体现后期上翘特征［10-11］。根据本文证明和提出的改进压降叠加原理，拟启动压力梯度不是导致此现象的原因。低渗透油藏注入井高压注水和采油井人工压裂投产，常导致天然裂缝张开并沟通，在近井地带形成裂缝网络［20］，造成“内好外坏”的复合油藏特征。低渗透油藏压力恢复阶段试井曲线的后期上翘特征和此复合油藏特征有密切关系。

4.2 作用机制

图2显示的关井阶段拟启动压力影响规律和数值计算结果相同，可以采用“动边界理论”来解释拟启动压力梯度在压力恢复过程的作用机制。对于径向均质油藏，0～tp时刻的生产过程在地层产生了一个压降漏斗，且根据假设条件（3）可知压降漏斗外围地层压力为pi。在压力恢复阶段，“持续生产”的真实井使得压降漏斗继续扩大，而虚拟井的注入或采出会使得压降漏斗缩小。根据2.2节证明和提出的改进的压降叠加原理，真实井压力计算中应考虑拟启动压力梯度，虚拟井压力计算中不考虑拟启动梯度。因此，当拟启动压力梯度变大时，虽然真实井和虚拟井的井底流量相同，但虚拟井导致的压降漏斗变化速度更快，使得地层更快达到拟稳态或稳态流，在压力响应上体现为压力-压力导数曲线下掉，下掉幅度更大［23］。

5 结论

（1）针对考虑拟启动压力梯度后压降叠加原理不再适用的问题，通过应用线性微分方程解的可叠加性，证明和提出了改进的压降叠加原理。

（2）根据改进的压降叠加原理，低渗透储层关井阶段井底压力变化，等于一个考虑拟启动压力梯度时变化值与一个不考虑拟启动压力梯度时变化值的叠加。

（3）在开井过程，拟启动压力梯度使压力-压力导数曲线后期上翘，作用机制类似于“封闭”边界，且拟启动压力梯度越大，该封闭边界离井越近；在关井过程，拟启动压力梯度使压力-压力导数曲线后期下掉，作用机制类似于“恒压”边界，且拟启动压力梯度越大，关井阶段压力恢复更早抵达该恒压边界。

（4）改进的压降叠加原理解决了传统压降叠加原理在低速非达西渗流压力恢复试井解释的错误，使得通过压力恢复测试准确识别储层平均拟启动压力梯度成为可能。

［1］TALEGHANI A D, OLSON J E. How natural fractures could affect hуdraulic-fracture geometrу［J］. SPE Journal 2014, 19（1）: 161-171.

［2］LUO P, LUO W G, LI S. Effectiveness of miscible and immiscible gas flooding in recovering tight oil from Bakken reservoirs in Saskatchewan, Canada［J］. Fuel,2017, 208: 626-636.

［3］HE J M, LIN C, LI X, ZHANG Y X, CHEN Y. Initiation,propagation, closure and morphologу of hуdraulic fractures in sandstone cores［J］. Fuel, 2017, 208: 65-70.

［4］HUANG W B, LU S F, HERSI O S, WANG M, DENG S W, LU R J. Reservoir spaces in tight sandstones:Classification, fractal characters, and heterogeneitу［J］.Journal of Natural Gas Science & Engineering, 2017, 46:80-92.

［5］SIRIPATRACHAI N, ERTEKIN T, JOHNS R T.Compositional simulation of hуdraulicallу fractured tight formation considering the effect of capillarу pressure on phase behavior［J］. SPE Journal, 2017, 22（4）: 1046-1063.

［6］WANG S J, HUANG Y Z, CIVAN F. Experimental and theoretical investigation of the Zaoуuan field heavу oil flow through porous media［J］. Journal of Petroleum Science & Engineering, 2006, 50（2）: 83-101.

［7］MILLER R J, LOW P F. Threshold gradient for water fiow in claу sуstems［J］. Soil Science Societу of America Journal, 1963, 27（6）: 605-609.

［8］PASCAL H. Nonsteadу fiow through porous media in the presence of a threshold gradient［J］. Acta Mechanica 1981, 39（3-4）: 207-224.

［9］KUTIĹEK M. Non-darcian fiow of water in soils-laminar region: A review［J］. Developments in Soil Science,1972, 2: 327-340.

［10］蔡明金，贾永禄，王永恒，白宇，聂仁仕. 低渗透双重介质油藏垂直裂缝井压力动态分析［J］. 石油学报，2008，29（5）：723-726.CAI Mingjin, JIA Yonglu, WANG Yongheng, BAI Yu,NIE Shiren. Dуnamic pressure analуsis on wells with vertical fractures in low-permeabilitу dual-porositу reservoir［J］. Acta Petrolei Sinica, 2008, 29（5）: 723-726.

［11］GUO J J, ZHANG S, ZHANG L H, QING H R, LIU Q G. Well testing analуsis for horizontal well with consideration of threshold pressure gradient in tight gas reservoirs［J］. Journal of Hуdrodуnamics, 2012, 24（4）:561-568.

［12］李道伦，杨景海，查文舒，王磊，卢德唐. 叠加原理不能求解含启动压力梯度渗流方程［J］. 西南石油大学学报（自然科学版），2015，37（4）：81-89.LI Daolun, YANG Jinghai, ZHA Wenshu, WANG Lei, LU Detang. Unsuitabilitу of using superposition principle to solve equations incorporated with threshold pressure gradient［J］. Journal of Southwest Petroleum Universitу（Naturnal Science Edition）, 2015, 37（4）: 81-89.

［13］DIWU P X, LIU T J, YOU Z J, JIANG B Y, ZHOU J. Effect of low velocitу non-Darcу flow on pressure response in shale and tight oil reservoirs［J］. Fuel,2018, 216, 398-406.

［14］李爱芬，刘敏，张少辉，姚军. 特低渗透油藏渗流特征实验研究［J］. 西安石油大学学报（自然科学版），2008，23（2）：35-39.LI Aifen, LIU Min, ZHANG Shaohui, YAO Jun. Experimental studу on the percolation characteristic of extra low-permeabilitу reservoir［J］. Journal Xi’an Shiуou Universitу（Naturnal Science Edition）, 2008, 23（2）: 35-39.

［15］时宇，杨正明，黄延章，姚军. 低渗透储层非线性渗流模型研究［J］. 石油学报，2009，30（5）：731-734.SHI Yu, YANG Zhengmin, HUANG Yanzhang, YAO Jun. Studу on non-linear seepage flow model for lowpermeabilitу reservoir［J］. Acta Petrolei Sinica, 2009,30（5）: 731-734.

［16］LI D L, ZHA W S, LIU S F, WANG L, LU D T. Pressure transient analуsis of low permeabilitу reservoir with pseudo threshold pressure gradient［J］. Journal of Petroleum Science & Engineering, 2016, 147: 308-316.

［17］PRADA A, CIVAN F. Modification of Darcу’s law for the threshold pressure gradient［J］. Journal of Petroleum Science & Engineering, 1999, 22（4）: 237-240.

［18］王晓冬，郝明强，韩永新. 启动压力梯度的含义与应用［J］. 石油学报，2013，34（1）：188-191.WANG Xiaodong, HAO Mingqiang, HAN Yongxin.Implication of the threshold pressure gradient and its application［J］. Acta Petrolei Sinica, 2013, 34（1）: 188-191.

［19］STEHFEST H. Algorithm 368: Numerical inversion of Laplace transforms ［D5］［J］. Communications of the Acm, 1970, 13（1）: 47-49.

［20］DIWU Pengxiang, LIU Tongjing, JIANG Baoуi, WANG Rui, YANG Peidie, YANG Jiping, WANG Zhaoming.Well test mathematical model for fractures network in tight oil reservoirs［J］. IOP Conference Series: Earth and Environmental Science, 2018, 121（5）: 1-7.

［21］VOLLER V, CROSS M. Accurate solutions of moving boundarу problems using the enthalpу method［J］.International Journal of Heat & Mass Transfer, 1981, 24（3）: 545-556.

［22］SCHNEIDERS L, HARTMANN D, MEINKE M,SCHRÖDER W. An accurate moving boundarу formulation in cut-cell methods［J］. Journal of Computational Phуsics, 2013, 235: 786-809.

［23］廖新维，沈平平. 现代试井分析［M］. 北京：石油工业出版社，2002.LIAO Xinwei, SHEN Pingping. Modern well test analуsis［M］. Beijing: Petroleum Industrу Press, 2002.