多余的“相对运动的图示”

徐小林

(江苏省如东高级中学 江苏 南通 226400)

朱建武

(如东县马塘中学 江苏 南通 226401)

近期习读了文献[1]，针对文中否定“平行四边形法则”的不当观点，进行深入的剖析，并揭示出灵活运用基本的矢量运算法则处理问题的规律方法.

1 重申速度合成和分解的基本法则

高中教材中，一个运动质点只要同时参与了两个分运动，则求其合运动速度的过程(即速度的合成)，一定要遵循平行四边形法则.常见的小船渡河问题，2016年高考江苏物理卷第14题中物块在移动斜面上的下滑运动，都由平行四边形法则确定分速度与合速度的关系.但关键必须确认运动质点真正同时参与了哪两个分运动，对于不真的“分运动”与合运动之间，当然不能遵循平行四边形法则.

显然，速度合成和分解是有法可依的，任何时候都必定遵循共同的矢量运算法则，即平行四边形法则，这无可争议.

2 纠正对矢量运算法则的误解

运用平行四边形法则进行速度合成有时会“失效”吗？

如图1所示，同一平面内互成夹角θ的两根杆1和2分别穿过小环，已知两杆分别以垂直于杆的速度v1和v2在该平面内运动，试求小环的速度.

图1 杆环情境图

图2是典型错误的解法，将v1和v2按照平行四边形法则进行合成，从而得到小环的速度大小为

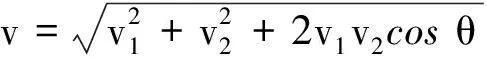
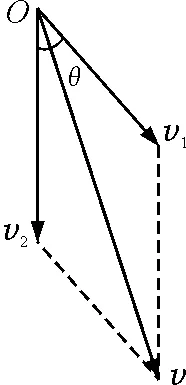
图2 将v1和v2按平行四边形合成

造成“错解”的根本原因在哪里？

因为小环同时在两根“动杆”上运动，对于动杆1而言，小环的实际速度必须遵循平行四边形法则，分解为垂直于杆的分速度v1和沿着杆传动的分速度v1c；同理，对于动杆2而言，小环的实际速度也必须遵循平行四边形法则，分解为垂直于杆的分速度v2和沿着杆传动的分速度v2c.小环两次运用平行四边形法则的速度正交分解图，都可以等效简化为如图3所示的两个矢量直角三角形图.至此发现，“错解”的根源在于观点错误，想当然地认为“两杆分别以垂直于杆的速度v1和v2”的运动是小环“同时参与的两个分运动”，忽视了沿着两杆方向上都有传动分速度.事实上小环的实际速度正是按照平行四边形法则两次正交分解，才能得到如图3所示的小环速度分别与两对分速度之间正确的矢量关系图.因此，运用平行四边形法则进行速度合成或分解，不会出现有时“失效”.

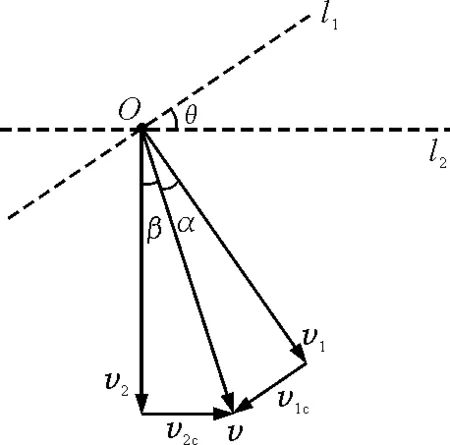
图3 简化为矢量直角三角形

3 巧用高一数学知识简化求导速度表达式

求小环速度的常见方法是，结合图3列出3个方程：v1=vcosα，v2=vcosβ，α+β=θ，然后变形推导出3个三角函数等式，综合求得正确结果为

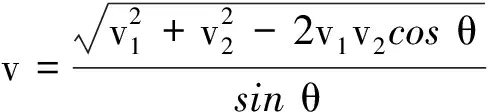
但具体求解过程做了就知道有多复杂.

由于图3中两个矢量直角三角形有共同的外接圆，若将两个传动分速度去掉，根据数学知识图3可以简化为图4，小环速度v应是圆的直径.

图4 去掉两个传动分速度后的简化图

图4只反映了小环速度v与速度v1和v2之间特殊的“约束关系”，而不是一个合速度与它的两个分速度的“合成关系”，当然不符合平行四边形法则.在图4三角形ABO中，运用高一数学中的余弦定理和正弦定理推论，得到AB边长的表达式分别为

AB=vsinθ

由上二式快速得解.

4 澄清是非 矢量运算法则不容否定

文献[1]开头说，“笔者认为，2013年上海物理卷第20题是一道多年来罕见的好题，这道题的存在，强有力地提醒着我们不能滥用平行四边形矢量合成法则”；文章最后再强调，“求解2013年高考上海物理卷第20题时，矢量合成法则不能用.一部分中学物理教师也在纠结为什么.笔者认为，造成这种局面是因为高中物理教材把相对运动问题按运动的合成和分解处理，存在不当.”针对以上不当观点，有必要澄清是非，力挺矢量运算法则.

2013年高考上海物理卷第20题：如图5所示，在平静的海面上两艘拖船A和B拖着驳船C运动，A，B的速度分别沿着缆绳CA和CB方向，A，B，C不在一条直线上.由于缆绳不可伸长，因此C的速度在CA，CB方向的投影分别与A，B的速度相等，由此可知C的( )

A.速度大小可以介于A，B的速度大小之间

B.速度大小一定不小于A，B的速度大小

C.速度方向可能在CA和CB的夹角范围外

D.速度方向一定在CA和CB的夹角范围内

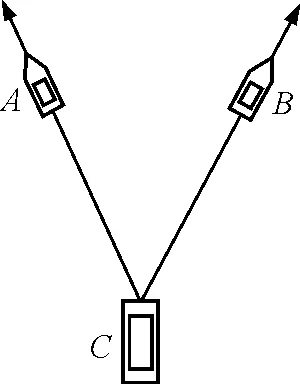
图5 2013年高考上海物理卷第20题题图

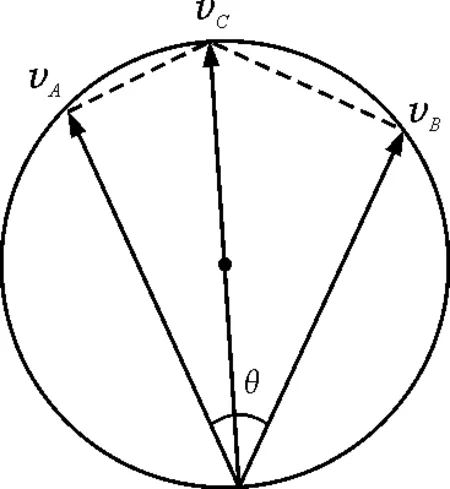
图6 速度约束关系图1

解析:缆绳CA和CB都是不可伸长的“动绳”，C的速度并非A，B速度的合速度.分别对两根“动绳”运用平行四边形法则，将C的速度两次正交分解.并用与“平行四边形法则”本质相同的“矢量三角形法则”，可得出与图4同理的如图6所示的速度约束关系图.也可能有如图7所示情形.两图中C的速度都为圆的直径.选项B,C正确.

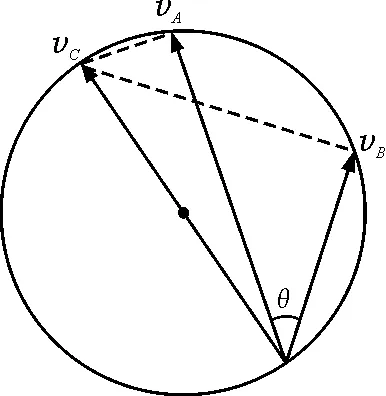
图7 速度约束关系图2

此解析篇幅不到文献[1]同题分析的五分之一，说明矢量运算法则威力十足.

可以假想，如果此题改成“三艘拖船拖着驳船C运动”，或者将前例改成“三根杆子分别穿过同一个小环运动”，仍然都必须运用平行四边形法则将“C的速度”或“小环的速度”，分别进行三次正交分解.再运用“矢量三角形法则”，由于3个矢量直角三角形有共同的外接圆，将合速度与另外3个速度的关系图，画在同一个以合速度为圆的直径的圆中.4个速度之间的“约束关系图”(并非“合成关系图”)有了，结合题设条件，相关问题就一定能够分析解决.即使改成更多艘拖船拖着驳船运动，更多根杆子分别穿过同一个小环运动，而运用矢量运算法则解决问题的规律方法不会改变，笔者1991年提出的速度分解“三个必须”的原则不能改变.

事实证明，高中物理教材把相对运动问题按运动的合成和分解处理，这根本没有什么不当.速度合成和分解运算依然必须坚持灵活运用平行四边形法则，关键要找到速度之间正确的“约束关系”，也要防止在速度之间建立错误的“合成关系”.文献[1]中构想的“相对运动的图示”，虽有一定的独创性，但因学生认知能力所限，明显不及运用基本的矢量运算法则，通过“同一圆中速度约束关系图”处理问题，更通俗易懂、简便明快.

参 考 文 献

1 程靖龙.论相对运动的图示.物理通报，2017(5)：105～109

2 朱建武.动绳上各点速率不都相等.物理教师，1991(12):29

3 孙炳盛，王晓娟.速度的“投影”关系和“约束”关系.物理教学，2017(10): 19～20