三力平衡问题的数学分析*
2018-06-15张忠献
张忠献
(邓州市第二高级中学 河南 邓州 474150)
在高中物理的学习过程中,学生会经常遇到三力平衡问题.解决此类问题的方法多是采用解析法,其实质是综合运用力的合成或分解及正交分解相关知识,利用物体受力平衡写出未知量与已知量的关系表达式,根据已知量的变化情况来确定未知量的变化情况.
由于三力平衡问题在静力学问题中占有较重的份量,故本文仅对求解三力平衡问题所运用的数学知识和方法做粗浅的探讨.
1 用相似三角形法求解三力平衡问题
【例1】(单选)如图1所示,质量均可忽略的轻绳与轻杆承受弹力的最大值一定,杆的A端用铰链固定,光滑轻小滑轮在A点正上方,B端吊一重物,重力为G,现将绳的一端拴在杆的B端,用拉力F将B端缓慢上拉,在AB杆达到竖直前(均未断),关于绳子的拉力F和杆受的弹力FN的变化,判断正确的是( )
A.F变大
C.FN变大
D.FN变小
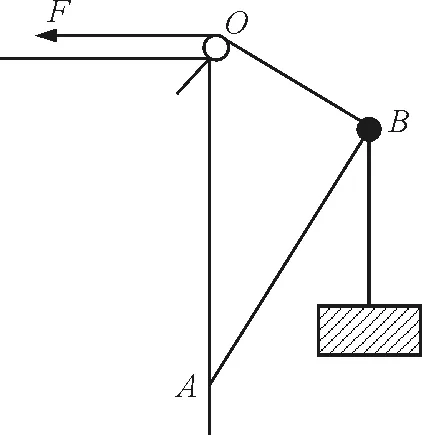
图1 例1题图
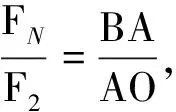
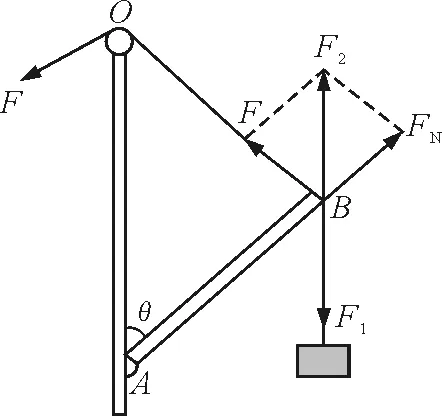
图2 例1分析图
点评:两个相似三角形的对应边成比例,这是平面几何中相似三角形的一个重要性质.将相似三角形对应边成比例用于求解三力平衡问题,可谓是另辟蹊径,别有洞天.该解法适用于物体受到了3个力的作用,其中一个力是恒力,另外两个力的方向都变化,且题目给出了空间几何关系.这样的解法使求解三力平衡问题走上了捷径.
2 用正弦定理求解三力平衡问题
【例2】 (单选)如图3所示,a,b两个小球穿在一根光滑的固定杆上,并且通过一条细绳跨过定滑轮连接.已知b球质量为m,杆与水平面成θ角,不计所有摩擦,重力加速度为g.当两球静止时,Oa绳与杆的夹角也为θ,Ob绳沿竖直方向,则下列说法正确的是( )
A.a可能受到2个力的作用
B.b可能受到3个力的作用
冰箱里头为什么有这么多东西?宝宝喜欢一个一个拿出来,看看东西没了,再一个一个放回去。这是建立空间概念的体验活动。妈妈可以关上电源,趁机清洁冰箱,引导他认识冰箱里拿出来的每一样物品,让他知道这些是食物,不能弄脏或打破。然后,拿来纸箱,和他一起动手做个纸冰箱,给他一些东西,让他去慢慢玩。
C.绳子对a的拉力大于mg
D.a的重力为mgcotθ
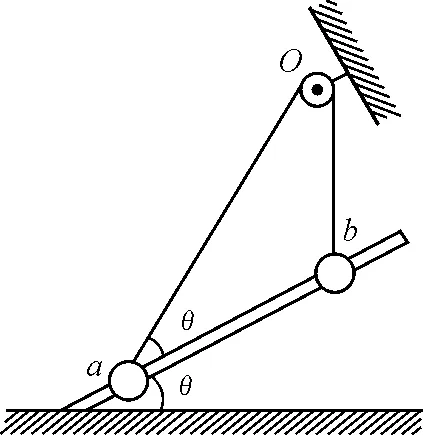
图3 例2题图
解析:a球受力分析图如图4所示,a球受到重力、绳子的拉力以及杆对a球的弹力,3个力的合力为零,选项A错误.对b球受力分析可知,b受到重力和绳子的拉力,两个力合力为零,杆对b球没有弹力,否则b不能平衡,选项B错误.由于b受到重力和绳子拉力处于平衡状态,则绳子拉力T=mg,同一根绳子上的拉力相等,故绳子对a的拉力等于mg,选项C错误.分别对a,b两球受力分析,运用合成法,如图4中所示,根据正弦定理列式得
解得
选项D正确.
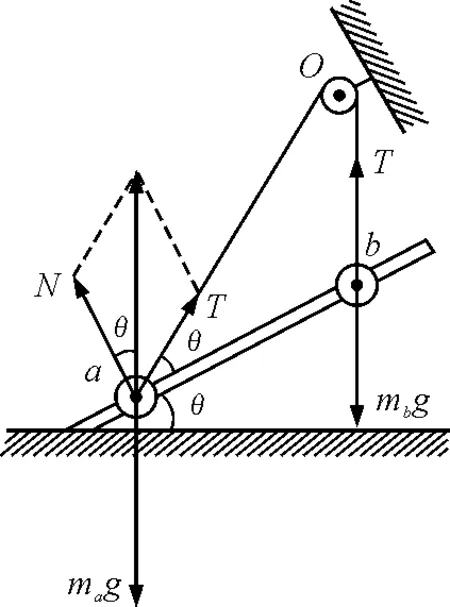
图4 例2分析图
点评:正弦定理(亦称拉密定理)是数学中的一个定理,它反映了三角形中3个边与相邻边夹角正弦值间相互制约的关系.在三力平衡问题中,这3个力组成一个首尾相连的封闭矢量三角形,故在求解三力平衡时运用正弦定理,就使得3个力及其夹角正弦值之间的关系一目了然,显示出快速解题的优越性.在求解三力平衡时,若已知或者容易算出3个力间的夹角和一个力时,选用正弦定理,可以说是明智之举.
3 用图解法求解三力动态平衡问题
【例3】(单选)如图5所示,一小球在斜面上处于静止状态,不考虑一切摩擦,如果把竖直挡板由竖直位置缓慢绕O点转至水平位置,则此过程中球对挡板的压力F1和球对斜面的压力F2的变化情况是( )
A.F1先增大后减小,F2一直减小
B.F1先减小后增大,F2一直减小
C.F1和F2都一直减小
D.F1和F2都一直增大
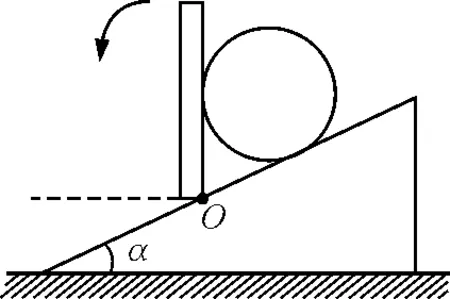
图5 例3题图
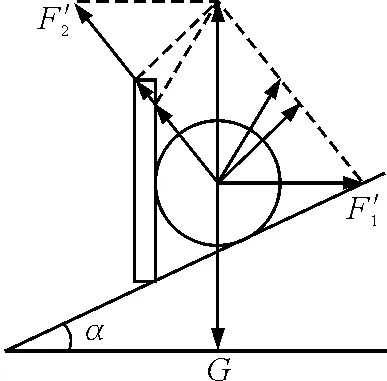
图6 例3分析图
点评:在共点力的平衡中,有些题目中常有“缓慢”一词,则物体处于动态平衡状态.解决此类问题常用图解法.若题目满足有一个力大小、方向均不变,另一个力方向不变,还有一个力的方向变化时,可画出这3个力的力矢三角形,结合大小、方向变化情况,分析得出未知量的变化情况.图解法体现了数学中数形结合的思想,它的优点是能将各力的大小、方向等变化趋势形象、直观地反映出来,大大降低了解题难度和计算难度.
4 用三角函数极值法求解三力平衡问题
【例4】(单选)如图7所示,倾角θ=30°的斜面固定,重为G的物体恰好可以沿斜面匀速下滑,现对物体施加一拉力(图中未画出),使物体沿斜面匀速上滑,则该拉力的最小值为( )

图7 例4题图
解析:物体恰好能沿斜面下滑,因此
mgsinθ=μmgcosθ
故
设拉力与斜面夹角为α时拉力最小,受力分析如图8所示.
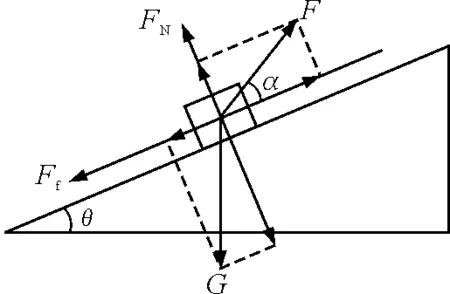
图8 例4分析图
根据力的平衡有
Fcosα=Gsinθ+Ff
FN+Fsinα=Gcosθ
Ff=μFN
联立得
令
得
即最小值
故C项正确.
点评:函数思想是数学的核心思想.该题型的解题方法是把角度θ作为参数,依据平衡条件得到未知量的函数表达式,利用三角函数关系得到它的极值.高中学生已经掌握三角函数相关知识,当遇到极值类问题时,他们还可以联想到导数等相关知识.这样做的好处是简化解题过程,拓宽解题思路.
参 考 文 献
1 张宝权.三力平衡问题与数学方法.中学理科参考资料,1993(3):13~16
2 杨志强.例谈高中物理三力平衡中的几种特殊解决方法.中学生理科应试,2016(5):49~50
