类比分析 把握规律
——谈2017年高考全国卷Ⅲ第25题
2018-06-15邵鹏飞
邵鹏飞 王 锋
(阜阳市第三中学 安徽 阜阳 236000)
近几年的高考物理卷中,无论是各省市的自主命题还是全国卷的题目,板块模型都是重要的考点,在2017年高考全国卷Ⅲ中就再次以压轴题的形式出现.这类题目涉及受力分析、运动学(含相对运动)、对象选择、过程分析、临界问题、假设法、图像处理,学生处理起来难度不小.现在,我们通过2014年高考江苏卷第8题和2013年高考全国卷Ⅱ第25题来寻找这类题目的解题规律并在2017年高考全国卷Ⅲ的第25题上加以应用.
1 分析案例 总结规律
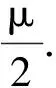
A.当F< 2μmg时,A,B都相对地面静止

C.当F> 3μmg时,A相对B滑动


图1 案例1题图
分析:面对这个题目考生容易出现的问题是被题目牵着走,试图将选项中的F逐一代入,发现不知道研究对象是谁,当然受力分析也无从谈起.究其根本原因在于学生的对象不明、场景不清.我们沿着以下思路来把问题理清.
问题1:随着F从零增大,A,B的运动会出现什么可能性?
提示:情况一,A先动,则B永远动不了;情况二,A,B一起开始运动,则随着F增大,A,B出现相对运动.(令A,B间的最大静摩擦力为f1,B与地面间的最大静摩擦力为f2,计算可知f1大于f2,因此是情况二)
问题2:F为多少时A,B开始运动?(令其为F1)
提示:此为临界1,B与地面间摩擦力达到最大静摩擦力,且A,B的加速度为零,即
问题3:F为多少时A,B开始相对运动?(令其为F2)
提示:此为临界2,A,B间摩擦力达到最大静摩擦力,且A,B的加速度相等,列式如下.
对整体有
对A有
F2-2μmg=2ma
解得
F2=3μmg
可知,0 规律总结: 第一,本题从解题的流程上看会遇到两大问题,即对象的选择、摩擦临界的处理.可以看出两大问题交织处理没有先后,且这两大问题的背后都有假设法的影子. 第二,关于摩擦临界的问题,两物体恰要相对滑动时有两个关键点,第一,两物体间的摩擦力恰好达到最大静摩擦力,第二,两物体加速度相等(可处理成整体). 案例2(2013年高考全国Ⅱ卷第25题):一长木板在水平地面上运动,在t=0时刻将一相对于地面静止的物块轻放到木板上,以后木板运动的速度-时间图像如图2所示.己知物块与木板的质量相等,物块与木板间及木板与地面间均有摩擦.物块与木板间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度的大小g=10 m/s2求: (1)物块与木板间及木板与地面间的动摩擦因数; (2)从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移的大小. 图2 案例2题图 分析: 对比案例1,本题突出运动学分析以及v-t图像的应用.对0 s~0.5 s由于木板的v-t图属于隐含条件,因此可同时获得木板和物块的牛顿第二定律方程,易得μ1=0.20,μ2=0.30;0.5 s以后学生容易直接认为两者共同减速,其实相对静止还是相对分离是需要判断的,处理办法是先假设两者一起减速,求得两者的共同加速度a=3 m/s2,进而求得两者恰要发生相对滑动的临界动摩擦因数 μ0=0.30μ1<μ0 即两者发生相对滑动,进而可求得 图3 案例2分析图 规律总结: 第一,假设法和临界问题.本题0.5 s以后物理情景的处理我们应坚持“情况不明,假设先行”的原则,切不可有未经证实的默认.而临界问题的处理正是沿袭着案例1的规律. 第二,v-t图像及阶段分析.在处理多物体、多阶段的运动学问题时要借助v-t图像打开思路;多阶段问题的解决关键是寻找时间节点.节点一旦确定,过程自然突破,这正是状态量和过程量在解题时的辩证关系. 2规律应用(2017年高考题) 【题目】(2017年高考全国卷Ⅲ第25题)如图4所示,两个滑块A和B的质量分别为mA=1 kg和mB=5 kg,放在静止于水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量m=4 kg,与地面间的动摩擦因数μ2=0.1.某时刻A,B两滑块开始相向滑动,初速度大小均为v0=3 m/s.A,B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10 m/s2.求: (1)B与木板相对静止时,木板的速度; (2)A,B开始运动时,两者之间的距离. 图4 2017年高考全国卷第25题题图 解题思路:根据前面两个案例的分析,我们可以综合阶段分析、对象分析 (含假设法和临界问题处理)、v-t图像来处理本题. 第一阶段:关键是木板的受力分析,易知其下表面最大静摩擦(临界)被突破,以2.5 m/s2向右加速,A,B则各自均以5 m/s2的加速度减速.第一阶段结束的时间节点为B和木板共速时,两者速度为1 m/s,时刻为t1=0.4 s. 第二阶段:关键在于B与木板共速后是否一起运动的问题.先假设B与木板相对静止,则 μ1mAg+μ2(mA+mB+m)g=(mB+m)a2 可知 而B与木板发生相对滑动的临界加速度为 a20=μ1g=8 m/s2 可知B与木板一起减速,进而可画出v-t图像如图5所示. 图5 第25题v-t图像 只要把握解决问题的规律和关键点,无论题目以哪种方式进行考查,学生都能迅速寻找到合理的解题策略,进而将问题解决.板块模型涉及的知识点丰富且考查角度多,但总的来说,解决这类问题主要是处理好对象的选择和过程的分析,同时结合假设法和临界处理则问题便可顺利解决.

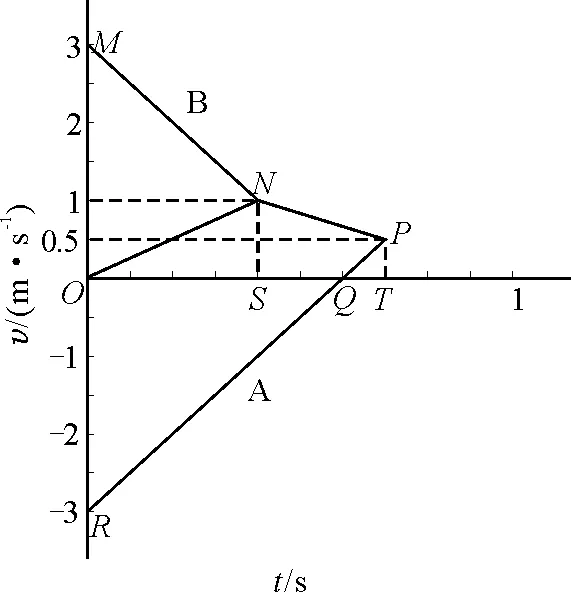
3 结束语
