TBM刀盘推力与扭矩预测方法分析

曹建锋，张 娜，梁国辉，冯乐森

CAO Jian-feng, ZHANG Na, LIANG Guo-hui, FENG Le-sen

(1.中国水利水电第四工程局有限公司，青海 西宁 810007；2.中铁工程装备集团有限公司，河南 郑州 450016)

随着我国铁路、调水工程、水电工程等基础设施建设的大规模开展，岩石隧道掘进机（TBM）在确保工程人员安全、施工速度、环保、保证施工质量和良好的经济效益等方面的优势而受到广大工程人员的青睐。

TBM的设计选型与关键参数计算是关系工程成败的首要环节。TBM主要用于硬质地层的开挖，由主机和后配套系统组成，主要解决如何利用滚刀高效破岩的问题。掘削破岩机构是TBM的关键性部件，掘进过程中的推力和扭矩是设计、制造TBM的两个重要基础参数，参数选择的正确与否是保证TBM顺利掘进的前提。

刀盘推力和刀盘扭矩是TBM总推力和扭矩的主要组成，是影响TBM掘进破岩效率的决定性因素，主要受到岩体地质条件的制约。因此，本文旨在分析刀盘推力和扭矩的计算方法，结合实际工程对TBM刀盘推力与扭矩进行预测，并与监测数据进行对比分析。

1 TBM推力与扭矩组成

TBM在施工推进中，由刀盘驱动系统驱动刀盘旋转，由推进系统给刀盘提供推进力，撑靴系统支撑洞壁承受支反力，在推进力的作用下滚刀切入掌子面岩石，在掌子面上留下不同半径的同心圆切槽轨迹（图1）。在滚刀的挤压下岩石产生破裂，并从岩体上剥落下来形成石渣，经溜渣槽滑落到主皮带机上，最后经矿车或连续皮带机出渣运输系统运出洞外。TBM掘进行程一般1.0～2.0m，完成一个行程后推进液压油缸收回，撑靴重新支撑进行换步，直至掘进贯通为止。

图1 掌子面切槽轨迹

1.1 总推力的构成

TBM在破岩推进时受到的推进阻力主要包括正面刀盘阻力、盾体滑行的摩擦力以及牵引后配套的阻力。正面阻力是滚刀的法向破岩阻力，是TBM总推力消耗的主要组成部分，也是TBM推力计算中的难点；盾体滑行的摩擦力主要是主机自重和作用在盾壳上的围岩压力产生的滑行摩擦力；后配套牵引阻力主要是拖拽后配套的滑行力。

TBM正面刀盘阻力F1主要是滚刀贯入岩石所需推力，即TBM刀盘推力为每个滚刀的滚压推力之和

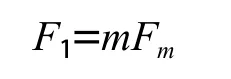
式中Fm——单个滚刀贯入岩石所需要的推力；

m——刀盘上安装的滚刀(单刃)的数量。

盾体滑行的摩擦力

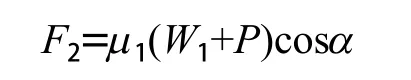
式中μ1——钢体与岩石的摩擦系数；

W1——TBM主机自重；

P——作用在盾壳上的围岩压力；

a——隧道轴线与水平方向的夹角。

牵引后配套的阻力

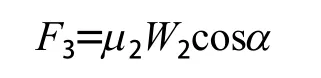
式中μ2—— 后配套轮与仰拱支护结构面的摩擦系数；

W2——后配套重量。

TBM总推力

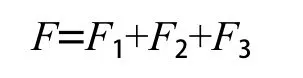
由上述可知，TBM总推力的确定关键在于刀盘推力的准确计算，直接体现在单个滚刀破岩力的受力分析。TBM刀盘推力是指推动刀具破岩所需要的合力，不包括克服TBM前进的各种摩擦力和牵引后配套所消耗的推力。

1.2 TBM扭矩的组成

TBM的掘进扭矩主要包括刀盘滚动阻力矩、岩渣搅拌所需要的扭矩、克服刀盘自重所需要的扭矩。刀盘滚刀阻力矩是滚刀破岩产生的滚动阻力扭矩，是TBM扭矩的主要构成；岩渣搅拌所需要的扭矩是滚刀破碎的岩渣随刀盘转动的阻力矩；克服刀盘自重所需要的扭矩即为刀盘空转时所需的扭矩。

因此，TBM掘进扭矩为

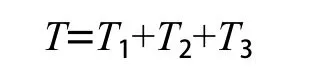
式中T1——刀盘滚动阻力矩；

T2——搅拌岩渣的阻力矩；

T3——克服刀盘自重所需扭矩。

刀盘滚动阻力矩计算

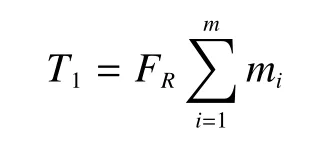
式中FR——单个滚刀滚动阻力；

mi——第i把滚刀距刀盘转轴的距离；

m——滚刀数量。

岩渣搅拌所需要的扭矩

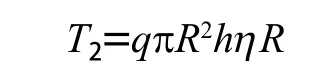
式中q——岩渣容重；

h——刀盘开口率；

R——刀盘半径；

h——每转切深，即贯入度。

克服刀盘自重产生的扭矩

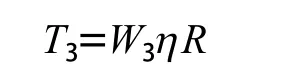
式中W3——刀盘自重。

由TBM刀盘扭矩构成分析可知，刀盘扭矩确定的关键在于滚刀滚动力FR计算。

滚刀受力分析是计算TBM刀盘推力与扭矩的关键基础，单个滚刀破岩力的计算关系着TBM推力与扭矩的预测，影响TBM工作能力与主要参数的设计计算。

2 滚刀受力分析

2.1 TBM掘进破岩过程中滚刀受力特点

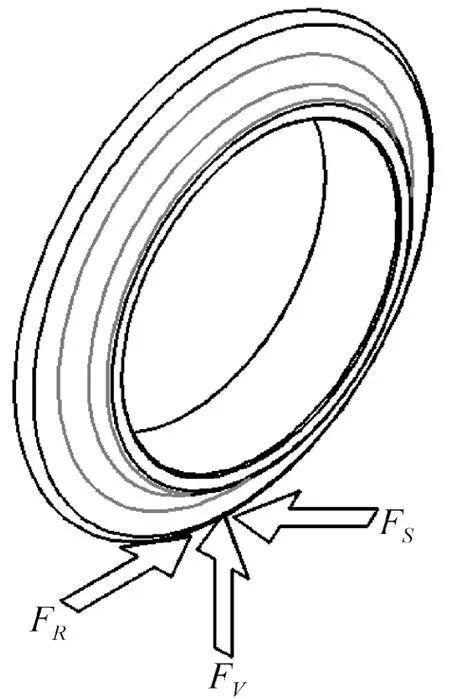
图2 滚刀破岩时的受力状态

TBM在破岩掘进过程中，滚刀在绕刀盘轴心公转的同时绕自身轴线自转，是两转动合成的运动。滚刀与岩石之间相互作用产生3个方向的作用力：垂直力FV、滚动力FR、侧向力FS（图2）。垂直力FV由刀盘推力提供，指向开挖面，是设计和校核TBM推进液缸和液压系统的依据；切向滚动力FR由刀盘扭矩提供，指向滚刀切向，是TBM刀盘驱动电机和转动系统设计校核的依据；侧向力FS由滚刀两侧岩石的挤压力以及刀盘离心力产生，指向刀盘中心，侧向力相对其他两个力较小，一般不予考虑。

2.2 滚刀受力预测模型

国内外学者对滚刀受力做了大量的理论和试验研究，建立了一系列滚刀受力预测模型，为TBM的刀盘与后配套设施的设计提供了依据，包括伊万斯（Evans）预测公式、秋三藤三郎预测公式、罗克斯巴勒（E.F.Roxborough）预测公式、科罗拉多矿业学院预测公式、Rostami预测公式、东北工学院岩石破碎研究室预测公式、上海交通大学640教研室预测模型、华北水电学院北京研究生部预测公式等。

Evans在1966年提出滚刀破岩过程中所受到的垂直力FV的计算模型，认为滚刀破岩时的垂直力FV与滚刀压入岩石破碎坑在岩石表面的投影面积A（图3中阴影）成正比，且比值为岩石单轴抗压强度σc，认为投影面积A为两条抛物线围成面积的一半。日本秋三藤三郎沿用了Evans的垂直力FV的计算理论，认为投影面积A是由两条双曲线围成面积的一半，并且补充了滚刀侧向力FS的预测公式。澳大利亚学者Roxborough同样认可Evans的滚刀垂直力FV计算理论，但是将投影面积A修正为一矩形面积，同时提出了滚动力FR和侧向力Fs的计算模型。这些滚刀受力模型都是在一定条件假设的基础上，通过理论分析计算得到。

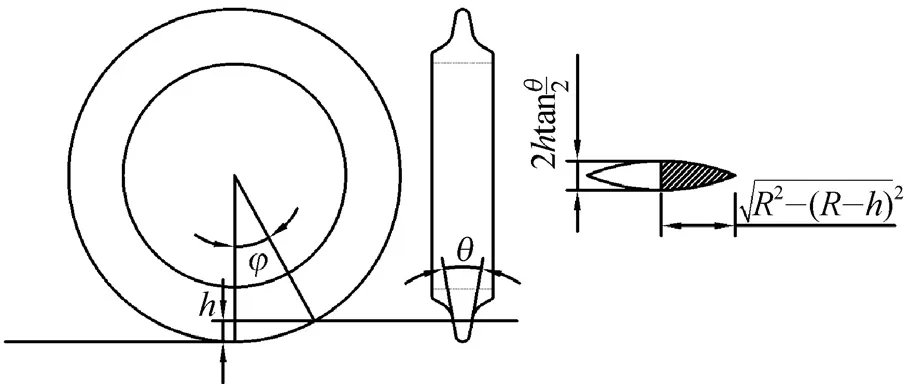
图3 滚刀破岩受力分析

随着试验研究条件的完善，科罗拉多矿业学院等众多学者则通过大量的试验数据建立了一些比较成熟的滚刀受力计算模型。科罗拉多矿业学院CSM预测公式由现行切割试验建立，认为滚刀作用下岩石破坏属于剪切和张拉破坏。Rostami预测公式是对科罗拉多矿业学院的CSM模型进行改进和完善，并基于大量的试验研究数据，拟合得到滚刀与岩石的单位接触面积上滚刀正压力与岩石抗拉压性能和滚刀几何参数的关系，国内外TBM设计中也广泛运用Rostami公式预测滚刀破岩力，得到设计人员的普遍认可。东北工学院岩石破碎研究室预测公式的计算方法与Evans理论相同，破岩所需垂直力FV与破碎坑在自由面上形成的破碎面积成正比。上海交通大学640教研室预测模型将滚刀与岩石的相互作用视为刀刃与岩面为两圆柱体的相互挤压，接触形式为线接触。华北水电学院北京研究生部预测公式认为滚刀的破岩是挤压、裂纹张拉及剪切的综合作用。

3 刀盘推力与扭矩计算

3.1 某山岭引水隧洞

某引水隧洞中部分地段地貌为丘陵及沟谷，山势较陡，山脊岩石裸露，植被不发育，沟谷季节性流水，岩性主要为石炭系中下统磨盘山组灰岩。桩号70+020位置处隧洞埋深15m，岩性为石灰岩，III级围岩，岩石主要物理力学参数：单轴抗压强度89MPa，抗拉强度5.8MPa，粘聚力12MPa，内摩擦角50°，抗剪强度23.5MPa，弹性模量48.9GPa，泊松比0.23。该工程TBM刀盘直径8m，安装56把19寸滚刀，滚刀直径483mm，刀刃宽20mm，平均刀间距71mm，贯入度7.6mm。

基于工程地质条件和TBM滚刀相关参数，采用各滚刀受力预测模型计算单个滚刀的垂直力和滚动力，进而得到TBM刀盘推力和扭矩，如表1所示。

从表1可以看出，各理论计算结果相差较大。通过实际工程监测得到，刀盘转速7r/min，TBM总扭矩2 421kNm，TBM总推力15 047kN，推进速度3.51m/h，贯入度8.35mm。TBM由盾体周围的摩擦阻力和后配套牵引阻力之和为5 650kN，刀盘自重和岩渣引起的扭矩约150kNm。TBM实际刀盘推力为9 397kN，刀盘扭矩为2 271kN。对比结果显示，实测值与Rostami预测公式计算结果相近，东北工学院预测公式结果偏大，其他理论结果偏小。

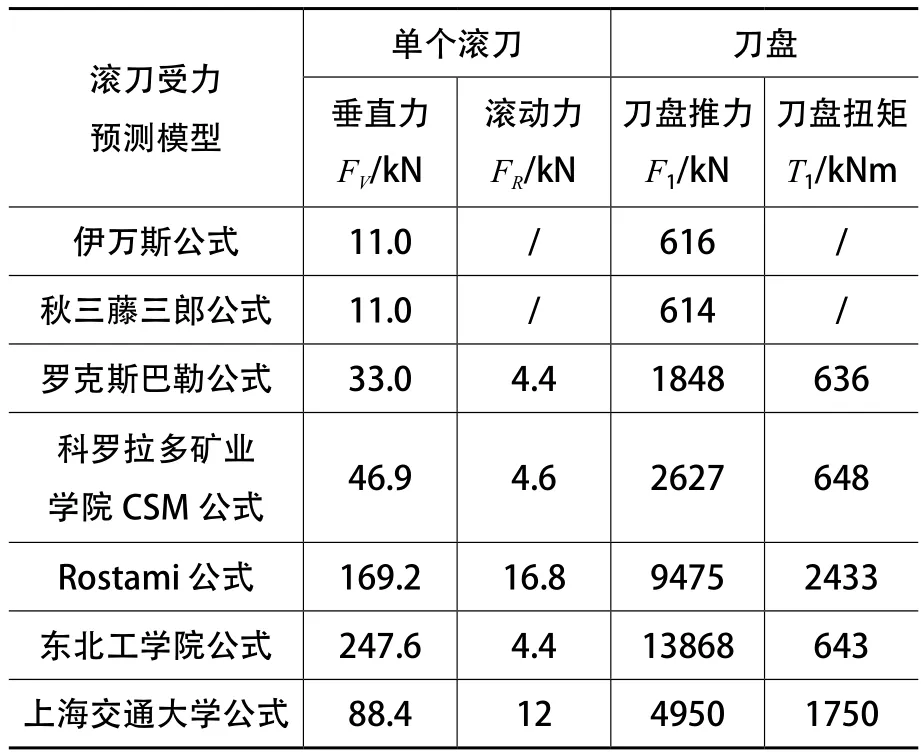
表1 TBM刀盘推力和扭矩理论计算结果

3.2 各计算理论对比

通过以上计算对比发现，各理论公式的计算结果之间相差较大。Rostami预测公式能够较准确地计算滚刀垂直力FV和滚动力FR，与实测值相近，而东北工学院计算公式所得结果偏大，其他预测模型的计算值偏小，特别是伊万斯理论值过小。理论计算结果与真实情况相比存在一定的误差，原因是在滚刀预测模型公式的理论推导中，对滚刀的实际运动受力情况做了不同程度是假设，另外，各理论公式大都采用楔形滚刀刀刃进行分析计算，而现在实际中近似常截面平刃滚刀应用普遍，已经成为TBM刀盘上最主要的破岩滚刀。同时，理论公式均未考虑岩体节理、裂隙等不连续面的分布所造成的破岩效果的影响。

虽然上述滚刀受力理论计算结果与真实情况都存在一定误差，但Rostami预测公式能够基本反映滚刀破岩过程中的受力情况，为TBM刀盘推力和扭矩的设定提供校核依据，对TBM刀盘推力和扭矩计算的预测基本能够达到预期目的。

4 结 论

刀盘推力和刀盘扭矩是TBM总推力和总扭矩的重要组成部分，也是工程领域专家学者研究的热门课题，预测刀盘推力和扭矩的关键在于单个滚刀垂直力和滚动力的计算。本文总结了常用的一些滚刀受力预测模型，并将其应用于实际工程，预测刀盘推力与扭矩计算。通过理论计算与实测值对比发现，Rostami预测公式的计算结果与工程实际值接近，对TBM驱动能力设计具有一定的指导意义，为刀盘滚刀优化设计提供理论基础。

[1]Ates U，Bilgin N，Copur H.Estimating Torque，Thrust and Other Design Parameters of Different Type TBMs with Some Criticism to T BM s Used in Turkish Tunneling Projects[J].Tunnelling and Underground Space Technology，2014，（40）: 46-63.

[2]Evans I，Pomeroy C D.The Strength，Fracture，Ad Workability of Coal [M].Pergamon Press，1966.

[3]秋三藤三郎.盘形滚刀破岩理论[J].小松技报，1970，16(3)：43-51.

[4]杨金强.盘形滚刀受力分析及切割岩石数值模拟研究[D].北京：华北电力大学(北京)，2007.

[5]田 雨.考虑岩石围压与损伤的 TBM 盘形滚刀受力的数值模拟分析[D].天津：天津大学机械工程学院，2010.

[6]孙永刚.隧道掘进机刀盘工作状态及刀具参数的优化分析[D].沈阳：东北大学，2008.

[7]金国栋，杨恩德.刀具破岩机理简述[M].沈阳：东北工学院，1984.

[8]张照煌.全断面岩石掘进机盘形滚刀寿命管理理论及技术研究[D].北京：华北电力大学，2008.

[9]龚秋明.掘进机隧道掘进概论[M].北京：科学出版社，2014.