基于压缩感知的视觉有意义图像加密算法
2018-06-15曹圣楠杨宇光
曹圣楠 杨宇光
(北京工业大学信息学部 北京 100124) (nancymu10@sina.com)
随着计算机网络技术研究的不断深入,无论身处何时何地,人们都可以通过互联网进行信息的传递.为了更好地满足人们的需求,信息传输的形式从原有单一文字逐渐转换为能够存储更多数据内容的数字图像、音频等.然而,由于这些多媒体数据可能包含私人的、有价值的甚至机密的信息,在信息共享普遍化、便捷化的同时,阻止这些重要信息被泄露甚至篡改成为研究的热门课题.
为了增强针对图像加密的安全性,提高加密的运算效率,图像加密技术应运而生.与普通加密技术不同的是,它考虑到了数字图像的特性,并利用这些特性来设计加密算法.图像加密一般情况下可分为3个步骤:1)选择图像加密算法;2)根据算法获取密钥;3)根据保存的密钥解密.
图像加密算法最早起源于经典的文本加密理论和经典的密码体制,为保护秘密图像的安全传输、秘密信息的顺利传递,防止非法用户获取其中信息甚至篡改破坏,本文提出将秘密图像完全掩盖,只有合法接收方才可以通过事先得到的相关信息或者解密方法解密得出原有图像.由于图像大数据量的特征,如何提高并改善加密算法的效率值得人们深入研究.如今的加密算法主要有2种加密机制:无意义和有意义的加密.无意义加密意图使秘密图像完全混乱且看起来像随机噪声,而有意义加密试图将秘密图像隐藏在另一封面图像中,因此,封面图像实际上加密了秘密图像.相比于随机噪声,有意义的封面图像不会引起人们的怀疑,即使非法用户窃取了它,大部分人都会认为该图像是原始的且不会尝试去破解它,由此可见,有意义加密比无意义加密更安全.
压缩感知(compressive sensing, CS)[1],有时也被称为compressive sampling.它的思路是在获取数据的同时就对其进行压缩,而且这种压缩能保证不失真(低失真)地恢复原始数据,这与传统压缩方式不同,可以降低采集信号的存储空间和计算量.
因此,本文设计并实现了视觉有意义的图像加密算法,通过这种算法加密的图像,在视觉上和未加密图像一样正常,可以起到减少图像被攻击概率的作用.与此同时能够抵抗部分数据丢失,具有一定鲁棒性.
基于图像数据量大、冗余度高并允许一定失真的特征,加密算法先后采用压缩感知技术与小波变换技术对图像进行加密.在经过对图像的压缩感知预加密处理后,将其观测值嵌入到封面图像小波变换的高频系数中,然后发送方通过安全通道将压缩感知及小波变换所需参数即密钥传递到接收方,当接收方接收到加密的图像时,使用该参数(密钥)对加密图像进行解密,得到重构的秘密图像.
1 相关工作
目前,常用的图像加密方法有基于混沌系统的加密算法、自适应图像加密、数字水印算法、盲源分离图像加密算法、压缩加密方法等,为了提高图像加密的效率和效果,常常将某2种算法结合在一起使用.
张爱华等人[2]于2011年提出了一种基于斜帐篷映射的混沌图像加密系统的改良方法.为节省加密时间和空间的复杂度,首先利用单层小波变换的压缩感知算法对图像作初步处理,然后再利用离散斜帐篷映射,结合正弦迭代混沌系统对图像通过多次迭代运算实现图像加密.该算法的优势在于运用压缩感知对图像初始化,从而提高加密图像的安全性,但最后得到的仍为易引发攻击者怀疑的类噪声图像.叶闯等人[3]提出了一种基于人类视觉特性的小波域盲数字水印算法,通过借鉴人类视觉特性HVS算法思想自适应地嵌入水印信息,能够很好地达到水印嵌入透明性和鲁棒性的平衡.郭慧等人[4]提出了一种具有鲁棒性与数据嵌入能力的JPEG 图像格式兼容的加密算法,主要解决JPEG图像加密算法引起的比特流大小增加与鲁棒性较差的问题.刘涛[5]考虑到水印预处理单一置乱方法的较差安全性以及水印嵌入中低频系数较差的载体图像不可见性,提出将Arnold变换与Logstic混沌映射相结合的水印置乱方法,然后根据人眼视觉特性将置乱水印嵌入到小波图像高频子带的纹理区内.
Bao等人[6]提出用简单图像加密技术(如改变图像像素位置及值)对原始图像作预加密,然后用基于整数小波变换的内容转换(DWTCT)将预加密图像转换成视觉上有意义的加密图像并输出,解密过程与上述过程相反.Cao等人[7]提出利用耦合字典来构建封面图像和秘密图像之间的联系,并运用压缩感知来解密秘密图像.
综上所述,越来越多的图像加密并非只局限于其中的某一种,而是将2种甚至3种加密方法结合应用,这样既可以使每种加密方法的优点得到充分发挥,又可以相互补充短缺之处,从而扩大算法的应用范围,提高图像传输的可靠性.而且由于大数据时代的来临,研究学者已然开始进一步关注图像加密过程中空间复杂度的重要性.
2 算法设计
2.1 总体设计
视觉有意义的图像加密算法总体流程设计如图1所示:

图1 算法总体流程
2.2 基于离散小波变换的图像压缩感知
2.2.1构造正交小波变换矩阵
一般2维或3维图像数据并不满足稀疏条件,我们可以通过将原有矩阵映射到一个稀疏空间来得到其稀疏表示,在本算法中即为对原有数据作正交小波变换,得到其小波系数.
首先,需要构造一个正交小波变换矩阵作为稀疏基φ:
其中φi为N维列向量.
然后得到小波基为sym4的分解低通滤波器和高通滤波器,再由滤波器长度以及矩阵维度得到运算所需最大层数和最小层数,最后通过卷积运算和下采样构造变换矩阵.
2.2.2稀疏表示及编码测量
由上述构造方法得到的稀疏基使得数据在该正交基上展开为
(1)
其中x是N的有限维子空间向量,此时为近似K稀疏,即x只有K个非0项,其他项近似为0.
为提高重构图像质量,将图像低频系数置乱保留并连同置乱密钥一起输出作为该阶段的密钥之一,接下来只对高频系数作稀疏化及编码测量.
通过稀疏矩阵(正交小波变换矩阵)使图像高频系数稀疏化,该步骤会耗费一定时间,但是可以提高稀疏度.
构造高斯随机矩阵θ作为测量矩阵,压缩感知观测值为
y=θx,
(2)
其中x为稀疏化的原始数据,由式(1)可知x=〈S,φ〉=φTS,结合式(2),压缩感知观测值可写为
y=θx=θφTS=AS,
(3)
其中A为该图像S的感知矩阵,大小为M×N(其中M 2.2.3调整测量值 原始图像经过压缩感知后的测量值范围比较大,且有正有负,这使得如果将测量值按数位的方式分别嵌入到封面图像的不同频率中,封面图像可能会因为嵌入数据数值过大或者是负值的关系而失真,这有违密文有意义图像加密算法的初衷,所以在嵌入数据之前,需要对该测量值进行处理.本算法利用Sigmoid函数调整其范围到0~255之间,参考已有结论[8]: (4) 其中参数取值为 Xmax是测量值中的最大值,Xmin是测量值中的最小值,参数a2和a3的值并非常数,而是包含图像特征信息、具有自适应性的变化量. 将调整过后的测量值称为调整值,并将调整值应用于接下来的运算.将未调整前测量值中的最大值及最小值也作为该阶段密钥之一输出. 此时该阶段密钥集即为测量矩阵、稀疏矩阵、置乱密钥以及置乱后的低频系数、测量值的最大最小值.密钥会通过安全通道直接由发送方传输给接收方,该加密方法为对称加密. 2.3.1S变换 S变换是最简单的整数小波变换,是线性Haar小波变换的近似整数形式.通过对封面图像进行S分解变换,可以得到单层分解后的图像矩阵;因为变换是可逆的,所以若对分解后图像直接进行S重构变换,能够完全恢复原封面图像. 首先将封面图像灰度图像数据方阵分为偶数序列和奇数序列2个互不相交的子集和,每个子集的长度是原来的一半. 然后利用偶数序列和奇数序列之间的相关性,对每一行进行S分解变换,接着对每一列进行S分解变换,得到一层分解后的图像矩阵. 可将信号sj分解为低频部分sj-1和高频部分dj-1. S变换分解式为 dj-1,k=sj,2k+1-sj,2k, (5) 其中[]表示取整. 观测值嵌入完成后,对分解的图像矩阵作S重构变换,先对每一列进行S重构变换,再对每一行进行S重构变换,得到加密图像.S变换重构式为 sj,2k=sj-1,k-[dj-1,k], (6) 其中[]表示取整. 2.3.2调整值嵌入高频系数 当封面图像为灰度图像,即维度为2时,通过对封面图像作单层整数小波变换(S变换),得到小波系数,令CA=LL,CH=HL,CV=LH,CD=HH,将预加密图像P(即原始图像的调整值)嵌入到封面图像,其中高低频(HL)嵌入预加密图像P的百位数字,得到 (7) 低高频(LH)嵌入预加密图像P的十位数字,得到 (8) 高高频(HH)嵌入预加密图像P的个位数字,得到 CD(m,n)=P(m,n) mod 10. (9) 当封面图像为彩色图像,即维度为3时,先将封面图像根据红、绿、蓝通道分成R,G,B这3个灰度图像,并分别对各灰度图像作单层整数小波变换(S变换),得到小波系数,令 R:CRV=LH(R), G:CGV=LH(G), B:CBD=HH(B), 将预加密图像P(即原始图像的调整值)嵌入到封面图像R,G,B这3个灰度图中,其中预加密图像P的百位数字嵌入到R灰度图像的低高频,得到 (10) 预加密图像P的十位数字嵌入到G灰度图像的低高频,得到 (11) 预加密图像P的个位数字嵌入到B灰度图像的高高频,得到 CBD(m,n)=P(m,n) mod 10. (12) 基于整数小波变换的内容解密过程是加密过程的逆过程.首先对加密图像进行S变换,然后从高频系数中获取调整值,从而获得预加密重构图像;最后对调整值进行Sigmoid函数反变换,公式为 其中μ为测量值,ρ1为调整值,参数a1,a2,a3与加密阶段保持一致. 开发平台:Matlab R2014a; 运行环境:Windows 10. 本算法主要实现针对灰度图像的视觉有意义的图像加密.以下测试中封面图像皆为原始图像的4倍大小,且每张图像自身长宽相等,为2n. 图2(a) ~(d)分别为使用相同的封面图像以相同压缩比加密不同原始图像的测试结果. 图2(a)与图2(b)分别为待加密的原始图像;图2(c)与图2(d)分别为加密后的图像;图2(e)与图2(f)分别为得到的解密图像.由图2可看出该算法实现了视觉有意义的图像加密,且能够低失真地解密图像. 图3为图2(c)、图2(d)的灰度直方图,由此可以看出,将经过压缩感知方法加密压缩过后的预加密图像嵌入到封面图像频域中,生成加密图像的统计特性基本一致,无明显差别. 图4、图5为不同原始图像使用相同封面图像man.tiff作加密,分别体现了以相同封面图像加密二者时得到的加密图像与解密图像的差值.通过计算,当以采样率为50%加密二者时,图4的峰值信噪比为38.013 4 dB,图5的峰值信噪比为31.536 6 dB,从视觉效果上来看都较好地恢复了原图. 图6显示以不同封面图像加密同一原始图像的测试结果.图6(a)(d)为原始灰度图像;图6(b)为以普通灰度图像加密图6(a)得到的加密图像,图6(e)为以普通灰度图像加密图6(d)得到的加密图像;图6(c)为以普通彩色图像加密图6(a)得到的加密图像,图6(f)为以普通彩色图像加密图6(d)得到的加密图像. 对于彩色图像而言,可以将彩色图像依据红绿蓝通道分为3张灰度图像,再分别对其加密,最后可得到利用相同密钥、不同封面图像或以不同密钥、不同封面图像加密的3张加密图像,可作为本算法的扩展. 算法的目的是生成一个密文有意义即视觉上看起来与自然图片相似的加密图像.TMQI算法[9]作为一种客观的评估算法可以用来测评该算法下生成的加密图像的视觉效果.TMQI包含以改进的结构相似性指数为基础的多尺度信号保真度检测和基于自然图像亮度统计的自然性测量.TMQI的最终得分(Q)是以保真度得分(S)和统计自然性得分(N)为基础的.这3个得分都在[0,1]的范围内,分值越接近1说明质量越好.因为TMQI是为彩色图像设计的,所以图6(c)、图6(f)所显示的加密图像是可以评估的.TMQI的结果如表1所示: 图2 以相同封面图像加密不同灰度图的测试结果 图3 加密图像的灰度直方图对比 图4 cell.bmp的测试结果 图5 camera.tiff的测试结果 图6 分别用灰度、彩色封面图像加密灰度图像的测试结果 表1 TMQI测试结果 保真度得分(S)以及最终TMQI得分(Q)可以证明该算法下的加密图像接近自然图像.在一些图像加密算法中生成的加密图像为类噪声,在本算法中可以证明该问题得以解决.如果用户希望生成的加密图像具有更高的自然性,增大选取封面图像的尺寸可能是一种好的方式. 数据丢失是传输过程中不可避免的,一个好的加密算法应该能够具有良好的抗破损性能.图7(a)为512×512的加密原图,它解密可得到图7(c);在加密图像上剪切一块大小为100×100像素数据块,得到图7(b),通过解密可生成如图7(d)所示的解密图像. 相比于图7(c),图7(d)有一些模糊,说明失去了部分高频信息,但总体来说,峰值信号比达到27.599 4 dB,原始图像大致被还原,该算法具有一定的抗破损性. 图7 抗破损性能测试结果 本文提出的基于压缩感知的视觉有意义图像加密算法主要有以下优势: 1) 相比现在已有加密算法生成类噪声加密图像可能会带来的大量攻击和分析,该算法生成的加密图像通常被认为是普通的图像,在数量庞大的图像传输中,攻击者将很难从普通图像中区分或者定位加密图像,所以该算法能够以更高的安全等级保护原始图像. 2) 基于图像压缩感知的加密方法使得对原图像所需测量的成本降低,不必对所有像素点测量即可重构图像,且在后续的嵌入过程中因为嵌入的数据较少所以对于封面图像而言更不容易被发现. 3) 基于图像压缩感知的预加密使得该算法具有非限定密钥空间和一定密钥敏感性. 同时,本文所提出的算法亦有不足之处: 1) 因为涉及到加密过程中密钥的生成,对使用图像的尺寸大小有要求,长和宽必须相同且为2的指数倍;封面图像必须至少为原始图像的4倍大小.秘密图像越大,它加密后所生成的加密图像也就越大,对网络的存储量和处理速度的要求也就更高. 2) 该算法的加密时间主要与预加密处理的数据以及2个阶段共同生成的密钥有关,数据量越大,生成密钥越复杂,所需时间也就越长. 随着网络中图像数量的增加,图像内容的安全变得越来越重要.视觉有意义的图像加密试图将秘密图像隐藏在另一封面图像中,使得加密图像从外观上来看同其他普通图像并无明显区别,在大规模网络环境下,相比于随机噪声,该类加密图像不会引起人们的怀疑. 本文将基于离散小波变换的图像压缩感知与整数小波变换内容加密结合在一起,充分发挥压缩感知在数据采集过程同时进行压缩的优势,从而缩短了执行时间,而且能在保证不失真(低失真)的前提下恢复原始数据,降低了采集信号的存储空间和计算量;充分利用小波变换适用于非平稳信号的特性,由于小波变换后得到的高频系数主要表示边缘细节,低频系数主要表示轮廓,保留低频系数,使数据在不影响封面图像视觉效果的同时,将秘密图像信息嵌入高频,从而完成加密. 本算法通过Matlab语言实现.在经过大量测试后发现,本算法能够以更高的安全等级保护原始图像,具有非限定密钥空间和一定的密钥敏感性,能够抵抗常见简单攻击. [1]Fornasier M, Rauhut H. Compressive sensing[M]Handbook of Mathematical Methods in Imaging. New York: Springer, 2011: 187-228 [2]张爱华, 薄禄裕, 盛飞, 等. 基于小波变换的压缩感知在图像加密中的应用[J]. 计算机技术与发展, 2011, 21(12): 145-147 [3]叶闯, 沈益青, 李豪, 等. 基于人类视觉特性(HVS)的离散小波变换(DWT)数字水印算法[J]. 浙江大学学报: 理学版, 2013, 40(2): 152-155 [4]郭慧, 贺杰, 李琳. 具有鲁棒性与数据嵌入能力的JPEG压缩图像加密算法[J]. 计算机应用研究, 2016, 33(9): 2804-2809 [5]刘涛. 基于小波变换的图像复合加密算法[J]. 电子设计工程, 2017, 25(5): 179-182, 186 [6]Bao L, Zhou Y. Image encryption: Generating visually meaningful encrypted images[J]. Information Sciences, 2015, 324: 197-207 [7]Cao X, Wei X, Guo R, et al. No embedding: A novel image cryptosystem for meaningful encryption[J]. Journal of Visual Communication and Image Representation, 2017, 44: 236-249 [8]邹建成, 陈婷婷, 张波, 等. 一种基于压缩感知的数字图像加密新算法[J]. 北方工业大学学报, 2014, 26(1): 1-6 [9]Yeganeh H,Wang Z. Objective quality assessment of tone-mapped images[J]. IEEE Trans on Image Processing a Publication of the IEEE Signal Processing Society, 2013, 22(2): 657-667
2.3 基于整数小波变换的内容加密及解密
sj-1,k=sj,2k+[dj-1,k],
sj,2k+1=dj-1,k+sj,2k,
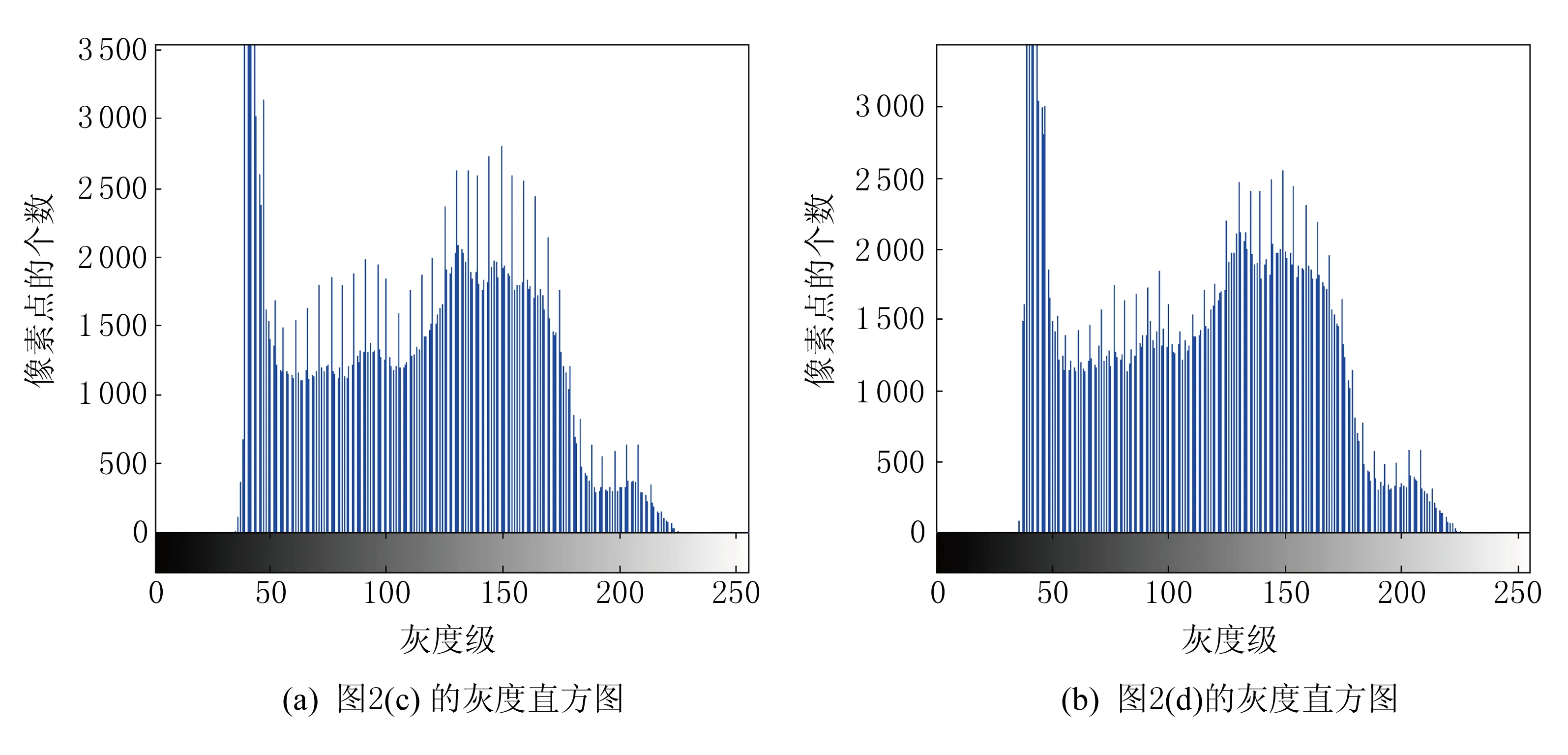
3 算法实现与仿真测试
3.1 算法测试
3.2 算法分析





3.3 抗破损性能

4 算法总结
5 结束语
