参数不确定的旅游环境承载力区间多目标优化

杨秀平，翁钢民 ，马玉泉，王晓云

（1.兰州理工大学a.经济管理学院；b.电气工程与信息工程学院，兰州 730050；2.燕山大学 经济管理学院，河北 秦皇岛 066004）

0 引言

旅游环境承载力的状况是旅游目的地可持续发展的重要保障，多数旅游目的地具有旅游者和当地居民为代表的多主体的聚集特征，考虑旅游业的季节性特征和多主体对旅游环境资源需求的差异特征，从多主体角度量化旅游环境承载力的研究，对促进旅游目的地多主体对旅游环境的需求，实现多主体的和谐共生具有重要作用。本文探讨差异情景下核心主体需求与满意水平的区间数；以旅游目的地人均旅游收益最大化、容纳的旅游者数量最大化、入境旅游者数量提升作为目标函数，建立旅游环境承载力优化配置的区间多目标优化模型；定义区间占优Pareto支配关系，利用区间参数多目标优化遗传算法对旅游环境承载力优化模型求解，以解决旅游环境承载力的量化测度中存在的不确定性问题；最后，以兰州市为例进行实证研究。

1 旅游环境承载力的界定与指标体系的构建

旅游环境承载力是指维持或者改进旅游环境系统的现存状态和结构组合，核心主体在一定需求标准下，其满意程度得以合理维持，此时可持续承载的适度规模下容纳的核心主体的数量。“适度规模”的测算需结合人均消费的合理规模和适度满意度水平与旅游目的地的开发潜力分情景展开。

本文从自然、经济、社会三方面构建旅游环境承载力指标体系，指标的筛选考虑客观性、科学性与数据的可得性，以指标体系涉及的资源条件构建旅游环境承载力优化模型的约束条件，见图1所示。

图1 旅游环境承载力指标体系

2 目标函数的构建

由于旅游环境承载力优化模型中参数为区间值，通过问题描述与转化，把旅游环境承载力优化问题转化为区间多目标优化问题。多目标优化问题得到的是Pareto优化解集或非被占优解集，见公式(1)。对应具体目的地的旅游环境承载力的优化问题，需根据决策者的个人偏好，从多目标优化问题的Pareto最优解集合中挑选出一个或一些解作为所求多目标优化问题的最优解。

其中：x为D维决策变量，Z为目标函数，N为优化目标总数；fi(x)为第n个子目标函数。g(x)看作是K项不等式的约束条件，所有约束条件共同构成了可行域；xd_min和xd_max作为向量搜索的下限和上限。公式(1)代表的多目标最优化问题包含最小化问题(min)和最大化问题(max)以及确定多目标优化问题。

本文在构建旅游环境承载力多目标模型时，通过旅游环境承载力指标体系中影响因素的开发状况与开发潜力φi、主体需求标准的适度控制等体现政府对旅游环境的干预；旅游企业除作为旅游环境承载力指标体系影响因素存在，构成约束条件外，企业从业人员成为复合型目的地旅游环境需求的主体之一。基于此，本文借鉴偏好参考点和偏好区间的思想，通过优化问题目标函数所在区域的子集，结合决策者偏好，界定决策者的偏好区域。以“人均旅游经济收入最大”、“核心利益主体容纳人数最大”与“入境旅游者人数最大”为目标函数，构建带区间特征的目标函数，设定22个约束条件(17个为旅游环境承载力指标体系中的影响因素约束、4个为核心主体发展趋势的区间约束)，以旅游旺季、淡季、平季设定三种情景，针对第i种情景的表达式，见公式(2)。

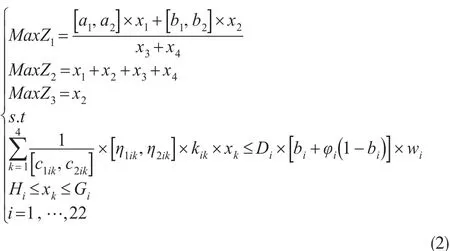
公式中：x1为国内旅游者数量；x2为入境旅游者数量；x3为城镇人口数量；x4为乡村人口数量；[a1, a2]、[b1, b2]为国内旅游者和入境旅游者的旅游消费区间(元/人)；[c1 i k'c2ik]为第k类核心主体对第i个影响因素的满意度区间范围；kik为核心主体在不同状况下的占比系数(%)；[η1ik'η2ik]为第i种资源被某一主体在特定情景下的消耗量；xk为第k类主体数量(k=1,2,3,4)；Di为i种资源总量；bi为某种资源的实际利用率；wi为开放时间/人均需要时间；φi为第i种资源的潜在可提供量的拓展程度，φi∈[0 , 1]；Hi和Gi为xi取值的区间范围。

3 旅游环境承载力多目标优化求解

参数未知，本文采用区间多目标优化方法进行求解。由于决策变量xi对应的目标函数为一组区间，给出区间占优Pareto支配关系，以比较解的优劣、找到问题的Pareto前沿，定义合理的区间数序关系。

3.1 区间占优Pareto支配关系

区间序关系有很多种，为简便采用Limboug和Aponte给出的区间序关系定义。称a在区间意义下不小于b，记为a≥INb，当且仅当a的下限和上限均不小于b的下限和上限，见公式(5)。

利用提出的占优关系修改NSGA-II的快速非被占优解排序方法，在NSGA-II中，由于Pareto占优关系的严格性，算法运行过程中会产生大量互不占优解，当利用拥挤距离法来保证群体多样性时，因为拥挤距离法的选择和Pareto占优关系的选择不具有一致性，有可能导致部分前沿面出现“退化”现象。为防止算法出现“停滞”或“退化”，对NSGA-II算法进行改进，当由在相同等级的两个个体中选择较优个体时，不再利用个体的拥挤距离，而是计算每个个体所占有的空间超体积，选择空间超体积大的个体。基于区间的超体积Pareto最优解集X的超体积的计算见公式(6)。

其中，xref是参考点，将区间参数多目标优化问题的近似Pareto最优解集的超体积，定义为一个区间，区间的上、下限分别称为最好、最坏超体积。当从属于相同等级的两个区间中选择较优区间时，计算每个区间的空间超体积，选择超体积均值大的区间个体。

3.2 不确定参数的旅游环境承载力优化求解步骤

根据区间占优Pareto支配关系，确定优化算法的基本步骤如下：

（1）参数的编码和译码：对旅游环境承载力参数优化时，需要对x1、x2、x3、x4参数进行编码和译码。设置种群规模为N，每个个体包含四个决策变量，从左到右依次为 x1、x2、x3、x4。

（2）初始化种群：根据旅游目的地的问卷调查与统计数据，估计出x1、x2、x3、x4四个参数的取值范围，在估计出的参数取值范围内采用均匀设计产生初始种群，使群体中的个体能够均匀的分布，这样可以使遗传算法能够在整个可行参数解范围内进行搜索；同时，设定遗传代数gen。

（3）计算目标函数值：计算初始化后的每个个体的目标函数值，设计“人均旅游经济收入最大(Z1)”、“核心利益主体容纳人数最大(Z2)”与“入境旅游者人数最大(Z3)”为目标函数。

（4）排序：利用基于区间的占优关系，按支配等级(支配等级为1的优先级别最高)降序排列σ%和tp。计算每层个体的超体积，由于旅游环境系统性能指标为区间数，需要计算其最坏超体积和最好超体积，取最坏超体积和最好超体积的平均值，作为其超体积测度。对于处于同一支配等级的个体，按超体积测度由大到小排序。得到最终的排序结果P(t)。

（5）选择：采用锦标赛选择方法，随机选取两个不同的个体进行比较，选择其中层数最小的(支配等级最高的)个体，在层数相同的情况下，选择超体积最大的个体，如若两者都相同，则选择其中任意一个个体。

（6）遗传操作：通过模拟二进制交叉和多项式变异操作，生成临时种群Q(t)。

（7）种群更新：将遗传操作产生的临时种群Q(t)和P(t)合并，得到规模为2N的新种群，通过基于区间的占优关系和个体的超体积测度对其排序，选择前N个性能较好的个体，作为下一代种群P(t+1)。

（8）停止：当遗传代数达到gen时，停止遗传操作，利用Topsis比较遗传操作产生的每一代个体中的σ%和tp的最优值，选择出一个相对最优值，计算出每组x1、x2、x3、x4对应的取值。

4 实证分析

4.1 研究设定

本文以兰州为例，对参数不确定的旅游环境承载力问题进行分析。设兰州市国内旅游者、入境旅游者“人次”与“人数”的折合比率为别为1.5与1.59。其次，在2013—2015年对核心主体需求标准区间与满意水平区间进行调研的基础上，结合国家相关的标准，界定核心主体对旅游环境需求标准的区间[ ]η1ik'η2ik与满意水平区间[c1ik'c2ik]。结合兰州市旅游环境2015年的具体统计数据，结合旅游环境承载力涉及资源的资源使用数值bij与未来开发状况的确定φij，可得出参数不确定的旅游环境承载力的区间多目标优化的目标函数和约束条件。

4.2 目标函数与约束条件的构建

根据2004—2015年国内旅游收入与入境旅游收入的统计，结合国内旅游者人数与入境旅游者人数，计算国内旅游者与入境旅游者的人均消费水平。入境旅游收入汇率的折算按照当年平均汇率进行折算。通过“人次”与“人数”、“美元”与“人民币”等的折算，得到2004—2015年兰州市国内旅游者的人均消费为[470.02，1290.75]元之间，入境旅游者的人均消费为[1866.08，3332.58]元之间。以10%为限度，将最大值与最小值进行扩展，得到对应的国内旅游者的人均消为区间为[423.02,1419.82]元，入境旅游者的人均消费区间为[1679.47,3665.84]元。以“旅游目的地人均旅游收益最大化、容纳的旅游者数量最大化、入境旅游者数量提升”作为目标函数。根据旅游业的季节性，将旅游目的地分为“旺季、平季、淡季”三种情景，通过问卷调查，得出核心主体需求的区间标准与核心主体满意度的浮动范围。

城市特色的突出对提升其旅游环境承载力具有重要作用，城市旅游资源必须有一定的吸引力，方程左边核心主体消耗的资源，不应该超过右端的资源总量。根据旅游目的地的特殊性，考虑旅游旺季、平季、淡季指标体系中影响因素的使用数值bi，确定φi的具体数值。以兰州市旅游旺季为例进行分析，见公式(7)。

4.3 参数不确定的旅游环境承载力优化求解

本文针对核心主体xi，对兰州市进行参数不确定的旅游环境承载力区间多目标寻优。在决策变量取值区间内均匀设计初始种群，设初始种群为500个，进化代数分别为50代，针对旅游目的地的旺季、平季、淡季三种情景下解的取值范围与均值，为了便于从空间角度观察解集的特征，本文给出旅游旺季、旅游平季、旅游淡季情景下的50组解的取值范围与均值，见图2所示。

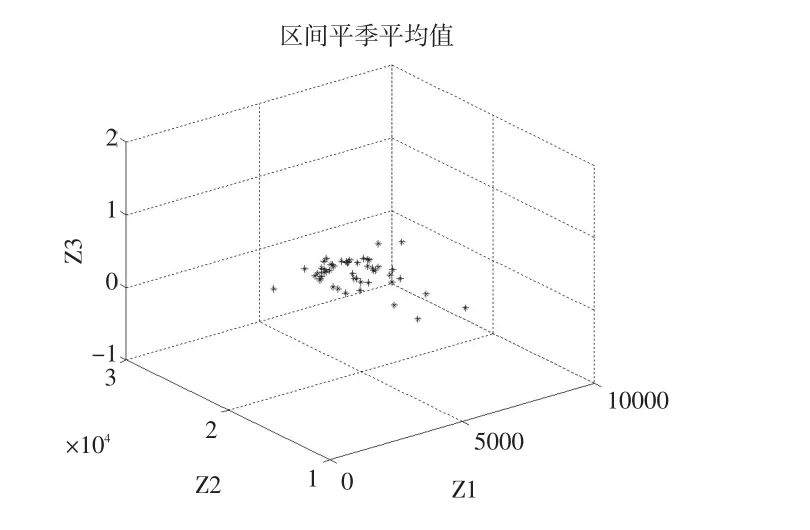
图2 三种情境下参数不确定的旅游环境承载力区间多目标优化的50组解的区间范围与均值

本文所构建的“人均旅游经济收入最大”、“核心利益主体容纳人数最大”、“入境旅游者人数最大”三目标区间优化模型，所得到的解为三维坐标系中的立方体，一个立方体对应一个解集，目标函数公式(2)中，只考虑Z1的不确定性。图2中的每个立方体区域都代表一个解的区间范围，因此区间内的个体是满足所有的约束条件，决策者也应该从这些立方体中选择合适的解,只考虑Z1中国内人均消费水平[ ]

423.02,1419.82与入境旅游者消费水平[1679.47'3665.84]，所得Pareto最优解集是三维坐标系的平面，考虑本文中的目标函数“核心利益主体容纳人数最大Z2”、“入境旅游者人数最大Z3”与不确定性参数无关，当Z1的不确定性参数发生变化时，目标函数Z2、Z3恒定不变，就会使得目标函数Z2、Z3的上下限相等，但是目标函数Z1随着不确定参数的变化而改变，所以，Z1不确定模型所求的解是三维空间中的平面。图2中的*代表每个区间解的中心。

结合旅游目的地的实际情况，在不同情景下，结合决策者偏好，解集的选取是多目标优化研究领域的探讨热点。本文以旅游旺季为例，列出部分解集以供参考，以旅游旺季Z1、Z2、Z3的部分优化解集为例对解的小数位四舍五入取整数，见表1所示。

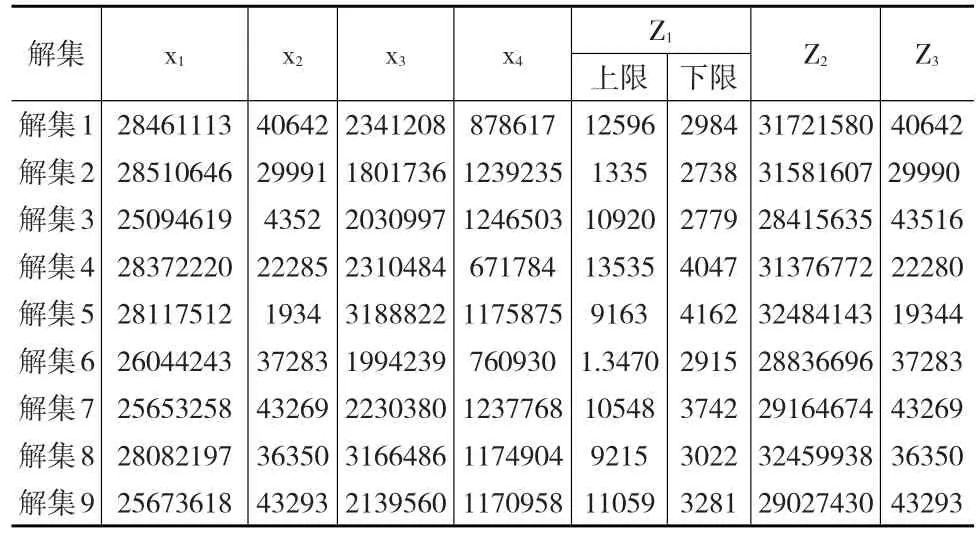
表1 旅游旺季Z1、Z2、Z3的部分优化解集

5 结论

随着旅游业的发展，导致旅游目的地的环境问题日益突出，对多主体旅游环境需求满足程度出现非均衡性，以较为科学的旅游环境承载力的量化研究为依托，促进旅游目的地的合理规划变得日益紧迫。鉴于旅游环境承载力优化研究中参数调整的困难，寻求更为科学的方法对旅游环境承载力进行优化研究，为旅游目的地的发展提供更为精确的量化指导，使相关的调控决策更加科学，提高旅游环境承载力的利用效率，成为学术界急需解决的问题。区间多目标优化理论与旅游环境承载力结合，在对传统的测算方法进行改进的基础上，通过优化模型不确定参数的分析，避免了前期研究需要大量精确数据的状况，不确定性参数的引入提升了旅游环境承载力研究的合理性与研究成果的实践适应性。

[1]Limbourg P,Aponte D E S.An Optimizaiton Algorithm for Imprecise Multi-objective Problem Function[C].Proc of IEEE International Conference on Evolutionary Computation.New York:IEEE Press,2005.

[2]Deb K,Pratap A,Agarwal S,et al.A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II[J].Evolutionary Computation,IEEE Transactions on,2002,6(2).

[3]王纯阳,黄福才.村落遗产地利益相关者界定于分类的实证研究——以开平碉楼与村落为例[J].旅游学刊，2012，（8）.