区域极点配置的状态反馈控制在高柔结构中的应用
2018-06-14李祚华陈朝骏滕军幸厚冰
李祚华 陈朝骏 滕军 幸厚冰

摘要: AMD控制系统中被控结构一般采用简化的计算模型,导致不确定性因素的存在,包括高柔结构的质量以及刚度的偏差,将影响控制器设计的准确性,而发展高柔结构的鲁棒AMD控制策略对土木工程的结构振动控制具有重要的理论价值和工程应用前景。基于区域极点配置算法设计了相应的鲁棒AMD控制器,在控制增益的计算过程中考虑不确定结构参数对计算模型精度的不利影响,以此提高了系统的稳定性。以10层结构为数值分析对象,以控制效果、AMD控制参数为指标,将所提出的控制器与基于经典极点配置算法的常规控制器进行性能对比,分析结果表明:对于含有较大不确定性的结构模型,所提出的控制方法具有更良好的控制效果以及稳定的控制参数;最后以4层框架试验模型的AMD控制系统为实例,验证上述数值分析结论的正确性。
关键词: 高柔结构; AMD控制系统; 区域极点配置; 线性矩阵不等式; 不确定结构参数
中图分类号: TU973; TU352文献标志码: A文章编号: 1004-4523(2018)02-0265-11
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.009
引言
主动质量阻尼器AMD[1](Active Mass Damper)控制系统不仅需具有良好的控制性能,还需具备較强的鲁棒性。系统的控制性能主要由系统的极点位置决定,极点配置算法是一种常用的AMD控制器设计方法[2]。但具有唯一解的极点配置算法,其鲁棒性较差[3]。
对此,学者们提出了一种将系统性能和鲁棒性相结合的控制器设计方法,即区域极点配置算法。基于该算法设计的控制系统,其瞬态特性将对应某确定区域内的极点对,而并非确定位置的极点对,可根据设计要求确定该区域的类型。区域极点配置算法因放宽了极点约束,使系统具有较强的鲁棒性。但受计算手段的约束,区域极点配置算法在出现之初,其求解问题并未得到很好的解决。直到20世纪90年代初,线性矩阵不等式LMI(Linear Matrix Inequality)的广泛应用使得该问题得到了解决,即将区域极点配置问题转化为线性矩阵不等式可行解的求解问题,再通过内点法有效地解决了上述凸优化问题。随后,LMI工具箱的出现提高了线性矩阵不等式的求解效率,推动了线性矩阵不等式在控制领域的运用[4]。在实际运用方面,Bai和Lu等研究了模糊系统的区域极点配置问题,从Lyapunov函数的角度给出了D区域稳定的定义,基于模糊Lyapunov函数方法并引入自由矩阵,保证模糊系统的闭环极点位于一个指定LMI区域,并以此进行控制器设计[5]。Datta等针对线性时不变多输入系统提出了一种凸优化算法,以减少基于区域极点配置算法的状态反馈增益矩阵的范数[6]。Yang等研究了基于区域极点配置的不确定线性连续时间系统的混合滤波问题,并设计了一种不确定性的独立滤波器[7]。基于区域极点配置算法,Zhang等针对有限频域内的不确定线性离散时间系统设计了故障检测滤波器[8]。经典控制理论研究基于精确化的结构模型,上述基于区域极点配置算法的控制系统,大多数考虑了不确定性输入信号的滤波问题。但实际工程中,高柔结构的参数包括刚度、质量等不确定量将降低了控制系统的性能[9]。因此,Xu等针对了具有参数不确定性系统,基于LMI理论提出无记忆状态反馈的鲁棒H∞控制器[10]以及输出反馈H∞控制器设计方法[11],单目标H∞控制不依赖于被控结构的精确计算模型,主要考虑了系统的鲁棒稳定性,但会牺牲系统的控制性能,而H2最优控制可以弥补这一不足,故将鲁棒控制器的设计当作一个结合控制性能与鲁棒稳定性的多目标优化问题。可基于区域极点配置的控制器设计方法,再令控制系统同时满足H∞干扰抑制和最优H2性能,从而完成对具有不确定结构参数的控制系统进行修正。
综上所述,本文首先对考虑结构参数不确定性的AMD控制系统状态空间方程进行描述。基于此,针对考虑了结构参数不确定性的某10层框架结构,基于区域极点配置算法设计其AMD鲁棒控制系统,并与基于经典极点配置方法的控制系统对比,其中,考虑的不确定参数包括刚度、质量。最后,针对10层框架进行数值模拟,并通过实际4层钢框架结构AMD控制试验系统验证数值分析所得结论的正确性。
1AMD控制系统参数不确定性问题描述具有不确定质量、刚度等参数的控制系统在外激励下的力平衡方程为M0+ΔM(t)+C0(t)+K0+ΔKX(t)=
Bww(t)+Bsu(t)(1)式中M0,C0和K0分别为结构的名义质量、阻尼和刚度矩阵;u和w分别为控制力输入和随机扰动输入;Bs和Bw分别为控制力和随机扰动的作用位置矩阵;ΔM和ΔK分别为质量矩阵和刚度矩阵的不确定量。
模型参数可表示为:M′=M0+ΔM=1+δMM0(2)
K′=K0+ΔK=1+δKK0(3)式中δM和δK分别为质量和刚度偏差系数。
令系统的状态向量为Z=XT,则式(1)写成状态方程为t=AZt+B1wt+B2ut(4)式中A,B1和B2分别为系统状态矩阵、外激励作用矩阵和控制力作用矩阵,可表示为:A=0I
-(M′)-1K′-(M′)-1C0,
B1=0
-(M′)-1Bw,B2=0
-(M′)-1Bs(5)具有不确定质量、刚度等参数的AMD控制系统可表示为t=A+ΔAZt+B1+ΔB1wt+
B2+ΔB2ut
Y1t=C1Zt+D11wt+D12ut
Y2t=C2Zt+D21wt+D22ut (6)式中ΔA,ΔB1和ΔB2为反映系统参数不确定性的实矩阵;Y1和Y2分别表示与H∞和H2性能指标有关的输出向量,其中Y1包括系统的位移、速度及加速度,而Y2包括系统的位移及速度(即Y2=Z),而且作为反馈信号用以控制力的计算。
上述系统控制力为u(t)=-GZt(7)式中G为闭环系统反馈增益矩阵。
2考虑结构参数不确定性的鲁棒控制器设计2.1极点配置区域形状的选择
极点配置算法通过将闭环极点配置在期望位置,使得系统获得期望性能。由于由系统自振频率、阻尼比及阻尼自然频率组成的系统极点决定了系统的阶跃响应,故通过调整系统极点位置可确保其自振频率、阻尼比及阻尼自然頻率满足设计要求。
极点配置算法是将系统的极点配置到确定的位置上,不完全适用于结构参数不确定的系统中;而基于区域极点配置的控制系统,将系统极点配置到给定区域,更具实际意义,可根据设计要求确定该区域的类型。
若存在对称矩阵L∈Rm×m与矩阵M∈Rm×m,使得复平面内区域D=s∈C:L+sM+MT<0(8)不为空集,则区域D称为线性矩阵不等式区域,定义其特征函数为fDz=L+sM+MT(9)LMI区域形状主要有α稳定裕度的区域、圆域、扇形区域以及条形区域等,或是任意有限多个LMI区域的交集也是一个LMI区域。
本文结合高柔结构极点分布的特点,选择用于设计鲁棒控制器的期望极点区域如图1中阴影部分所示。
图1极点区域
Fig.1Pole region
该集合由3种主要形式的区域形状组合而成,第一种主要形式是具有α稳定裕度的区域Dα=s∈C:x<-α(10)相应的区域特征函数为fDz=2α+s+(11)第二种主要形式为具有半径为r,圆心为(-q,0)的圆域,可表示为Dr,q=s∈C:s+q+q-r2<0(12)相应的区域特征函数为fDr,qs=-rq+s
q+-r=
-rq
q-r+s01
00+01
00T(13)第三种主要形式是扇形区域Dcs=s=x+jy:x,y∈R,tanθ<-yx(14)相应的区域特征函数为fDcss=sinθs+cosθs-
cosθs-sinθs+(15)该区域可用下列的集合描述Sα,r,θ={x+jy∈C:x<-α,
x+jy
2.2控制增益设计原理
本文鲁棒控制器的设计目标是使得闭环系统同时满足H∞性能、H2性能和闭环极点约束,其中,选择的极点配置区域如图1所述。
假定结构参数摄动矩阵为[4]ΔAΔB2=HFE1E2(17)式中F=I为不确定矩阵,为小于1的不确定常数。矩阵H,E1和E2可表示为:H=00
-K0M0-C0M0,
E2=0
BsδM+1-1-1C0,
E1=
δK+δK+1δM+1-1-10
0δM+1-1-1(18)将式(17)代到式(6)中,得t=A-B2G+HFE1-HFE2GZt+
B1+ΔB1wt
Y1t=C1-D12GZt+D11wt
Y2t=C2-D22GZt+D21wt (19)令=A-B2G+HFE1-E2G,1=B1+ΔB1,给定正常数γ,对于控制系统(19),且假定存在着正定对称矩阵X1,使得X1+X1T1X1C1-D12GT
T1-γIDT11
C1-D12GX1D11-γI<0(20)则可得状态反馈控制系统的H∞控制律[12]。
若给定对称矩阵Y和矩阵H,E,使Y+HFE+ETFTHT<0(21)对满足FTF T1-γI* C1-D12GX1D11-γI(23)式中带*号的子元素可根据矩阵的对称性得到。 式(21)可表示为Y+H 0 0FE1-E2GX100+ E1-E2GX100TFTH 0 0T<0(24)根据式(22)和(24)可转换为Y0+μH 0 0HT00+μ-1X1E1-E2GT 0 0· E1-E2GX100<0(25)若应用矩阵的Schur补性质,式(25)可等价为A-B2GX1+X1A-B2GT+μHHT*** T1-γI** C1-D12GX1D11-γI* E1-E2GX100-μI<0(26)对于控制系统(19),给定η>0,若存在着正定对称矩阵X2,Q,使得X2+X2T+1T1<0, -QC2-D22GX2 X2C2-D22GT-X2<0, D21=0, TraceZ<η2(27)则可得状态反馈的H2控制律[4]。 区域极点配置性能要求系统(19)的闭环极点位于给定LMI区域,这一性能得到满足的充要条件是存在着一个正定矩阵X3,使得下式成立[14]LX+MX3+MTX3T<0(28)在式(26)~(28)所述不等式系统中,容易发现X1,X2,X3,Q,G不是凸的,可通过找到一个公共的Lyapunov矩阵以解决该难题[4]。X=X1=X2=X3(29)假设W=-GX,则基于建立和求解下述的凸优化问题,可解决这一多目标控制问题minγ,X,Y,Zαγ+βTraceQ(30)s.t. AX+B2W+AX+B2WT+μHHT***
T1-γI**
C1X+D12WD11-γI*
E1X+E2W00-μI<0,
LX+MX+MTXT<0,
-QC2X+D22W
C2X+D22WT-X<0,
TraceQ<η20, γ<γ0
式中γ0,η0,α和β都是给定的数。
由问题(30)可知,本文主要提出了具有H2/H∞性能要求和闭环区域极点约束的状态反馈控制器设计方法,该问题可用LMI工具箱中的求解器mincx求解。
W′和X′为该问题的最优解,则不确定系统(19)的状态反馈控制律为U=W′X′-1Zt(31)2.3数值分析
本文建立了10层剪切型框架结构模型进行数值分析,结构平面布置如图2所示,结构总高度为33 m,总质量为875 t,层高均为3.3 m。其中,结构两个方向的主梁尺寸均为500 mm×250 mm(梁1和梁2),次梁(梁3)的尺寸为450 mm×200 mm,柱的尺寸为500 mm×500 mm。采用集中质量法建立该结构的质量矩阵;通过对结构每一质点层施加单位力,求得每一质点层的位移,进而组合成结构的柔度矩阵,再对其求逆可得结构的刚度矩阵。
该结构的AMD控制系统安装在第8层,仅控制结构的弱轴向水平振动,其关键参数如表1所示。10层框架结构的弱轴向平动各阶模态的振型参与质量系数、自振频率及阻尼比如表2所示。本文采用了常值阻尼比模型,各阶模态的阻尼比取为0.02;结构的振型参与质量系数表征结构振型对结构响应贡献度,而该结构的第一阶振型参与质量系数达到79.40%,因此第一阶振型对结构动力响应起决定性作用。
针对上述结构,基于2.2节为理论基础设计该框架结构具有区域极点约束的状态反馈控制器,并与基于经典极点配置算法的控制器对比,以此为基准验证该控制器是否拥有较好的鲁棒性。通过调试后选取区域极点参数为:α=0,θ=arccos0.05和r=7,q=0。
图2标准层结构平面图(单位:mm)
Fig.2The plan of each floor(Unit: mm)表1AMD系统的关键参数
Tab.1Key parameters of AMD
指标AMD重量/kg4000最大行程/m±1.1最大驱动力/kN55表2框架的振型参与质量系数、自振频率与阻尼比
Tab.2Modal mass participation ratios, frequencies and damping ratios of the frame
阶数振型参与质量
系数/%自振
频率/Hz振型
阻尼比179.400.140.0229.850.460.0234.100.850.0242.371.340.0251.561.950.02
控制系统的开闭环极点分布位置如图3所示。由图3(b)可以看出该系统的闭环极点分布在上述区域内,达到了控制系统的设计要求,因为该系统距离虚轴较远的闭环极点的实部与距离虚轴最近极点的实部比值大于5,后者附近也不存在闭环零点,因此,该距离虚轴最近的极点在控制系统的过渡中起主导作用,而且该主导极点也位于实轴(x轴)上,说明该配置过程能够考虑结构参数不确定性的影响,有效地提高系统阻尼。
选取合适参数之后,基于区域极点配置算法进行鲁棒控制器设计,以及基于经典极点配置进行控制器设计。当参数无偏差以及刚度最大偏差为-30%、质量最大偏差为20%时,对比各工况下两种控制器的性能,且两者的控制力均值在15 kN左右。在十年一遇风荷载作用下,两种工况的数值仿真分析结果如表3和4所示,表中数值包括系统的控制效果、AMD控制力和其行程,图4和5给出了结构第8层在风荷载作用下有无控制的时程曲线对比。图3控制系统开闭环极点位置分布图
Fig.3 Comparison of the positions of the open-loop poles and the closed-loop poles
表3结构响应控制效果对比(δK=δM=0)
Tab.3Control effectiveness of structural responses(δK=δM=0)
控制指标经典极点配置区域极点配置位移速度加速度位移速度加速度第8层44.2844.7133.5556.3255.9646.00控制效果/%第9层44.3244.8537.8456.2855.5044.49第10層44.3444.6334.2356.2054.9343.24控制力/kN15.0715.12行程/m0.160.15
表4结构响应控制效果对比(δK=-30%,δM=20%)
Tab.4Control effectiveness of structural responses(δK=-30%,δM=20%)
控制指标经典极点配置区域极点配置位移速度加速度位移速度加速度第8层28.3127.3314.5851.2650.9539.50控制效果/%第9层28.3227.7720.5751.1950.2036.66第10层28.3127.5918.7551.0849.3635.79控制力/kN15.0715.12行程/m0.160.15图4结构第8层响应时程及AMD参数时程对比(δK=δM=0)
Fig.4Comparison of structural responses to 8th floor and AMD parameters(δK=δM=0)
图5结构第8层响应时程及AMD参数时程对比(δK=-30%,δM=20%)
Fig.5Comparison of structural responses to 8th floor and AMD parameters(δK=-30%,δM=20%)
图4,5以及表3,4结果表明:(1)当结构参数无偏差时,基于经典极点配置算法的控制器以及基于区域极点配置算法的控制器均能明显减轻结构的风振响应;但在AMD控制力及其行程输出相当的情况下,前者的控制效果基本在33%~45%之间,而后者的基本在43%~55%之间,即基于区域极点配置算法设计的控制器的控制效果相对较好,证明了该控制器的设计中有优化的过程;(2)在结构刚度、质量都具有大偏差时,经典极点配置控制方法的控制效果较差,结构第8层的加速度最大控制效果仅为14.58%,结构位移、速度、加速度控制效果分别下降了16.03%,17.39%,18.97%;而区域极点配置控制方法较为有效,结构位移、速度、加速度控制效果分别仅下降了5.12%,5.57%,7.83%。因此,对于结构模型中含有较大不确定性的工况,基于区域极点配置的控制方法有较为明显的优势。
3实验验证
本试验系统由一栋单跨4层钢框架结构及其AMD控制系统组成[1],如图6所示。
图64层钢框架实物图
Fig.6Picture of the four-storey steel frame3.1试验系统简介
先计算得到该框架结构各个楼层的质量,再利用集中质量法求得结构的质量矩阵;结构刚度矩阵则由根据钢框架的实际构件体积、密度及其设备建立的有限元模型计算得到,再利用实测到的系统自振频率对其进行修正;系统的阻尼矩阵可由测试得到的阻尼比平均值通过文献[15]的式(2.3.28)建立。
该钢框架的动力特性介绍如表5所示,表中包含了结构各阶模态的振型参与质量系数以及自振频率。其中,结构第一阶振型对结构动力响应起主要贡献,第一阶的振型参与质量系数为85.57%接近于1。而第一阶振型时顶部响应最大,因此在试验系统中将AMD控制器放置于顶层,使其能起到更好的控制效果。
表5试验系统振型参与质量系数、自振频率
Tab.5Modal mass participation ratios and frequencies of the experimental system
阶数振型参与质量系数/%自振频率/Hz185.570.1428.950.4633.390.8642.091.27
本文所述的AMD系统主要由伺服驱动器、控制电机、板卡型号DS1103的dSPACE、EtherCAT总线以及微型计算机组成。控制电机由广东省深圳市大族激光公司生产的LMCF210201直线控制电机,EtherCAT总线系统由德国BECKHOFF公司生产的EL3008输入端子、EL4034输出端子、EK1100耦合端子、AX5000伺服驱动器组合而成。外激励加载系统由旋转电机、变频调速器以及配重组成。测量系统包括对结构弱轴向的位移以及加速度水平振动响应进行测量,系统采用GT02型力平衡加速度传感器以及MICRO-EPSILON系列激光位移传感器,用dSPACE系统作为测量系统的采集仪;力平衡式加速度传感器放置于各层楼板与钢柱的交点,激光位移传感器放置于与被控结构分离的固定支座上且测点定位在各层楼板与钢柱的交点。其中,将框架弱轴向水平加速度信号作为系统反馈信号,用以计算实时控制力。
3.2试验结果分析
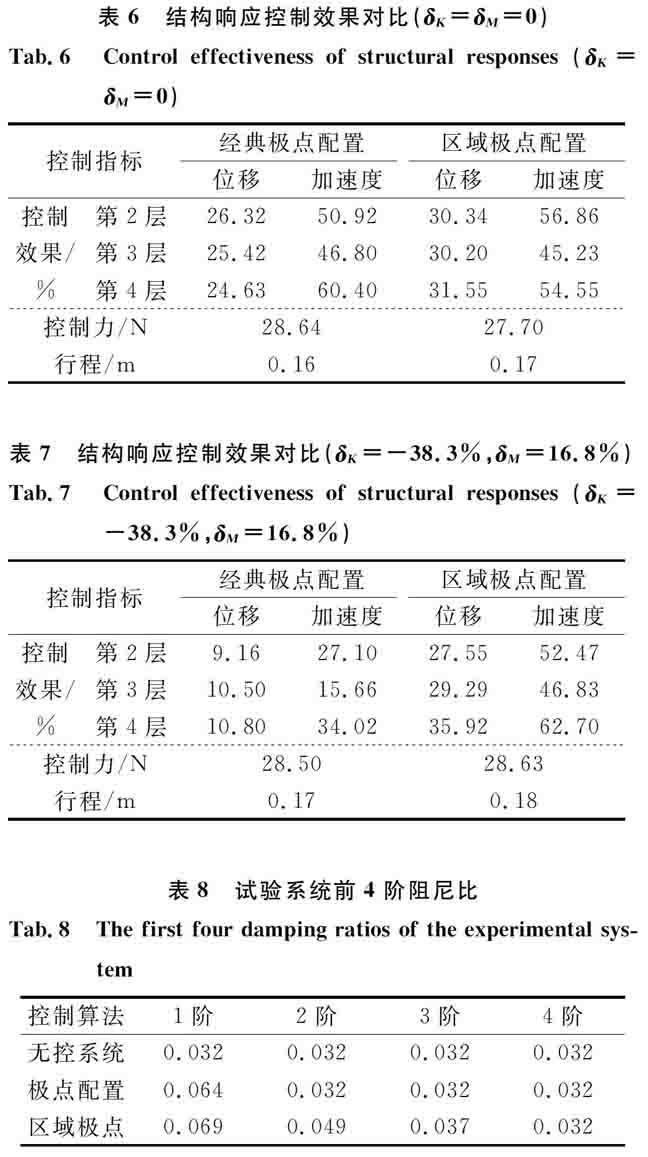
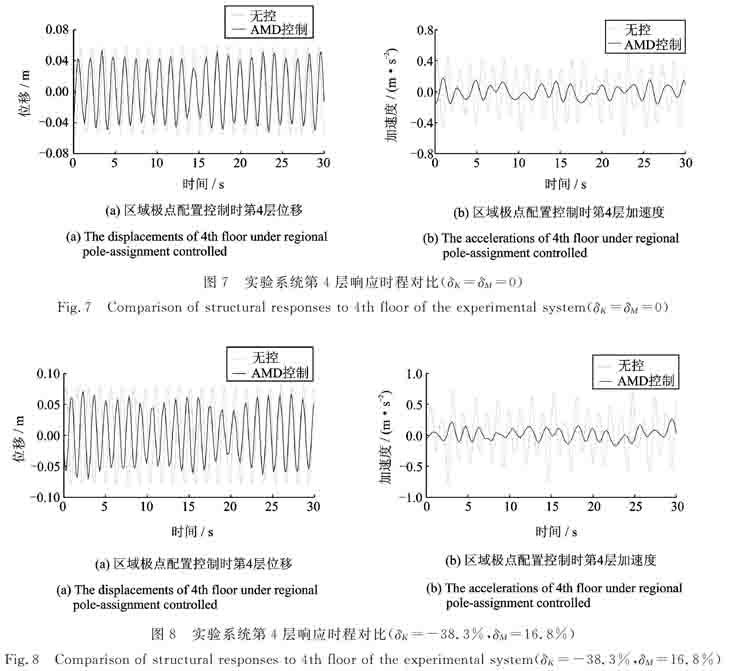
针对上述试验系统,本节基于区域极点配置算法和经典极点配置算法分别进行试验系统的控制器的设计,并进行两者性能的对比分析,考虑了两种不同工况包括无质量、刚度偏差及刚度偏差为-38.3%、質量偏差为16.8%。楼层质量需要通过在框架上施加额外配重来改变,具体的质量偏差由已知的各个楼层及其附加配重质量对比得到;刚度需通过调节连接螺栓的松紧程度来改变,具体的刚度偏差可通过对比刚度调整前后的刚度矩阵得到,而调整后的刚度矩阵由柔度法计算得到。试验分析结果如表6和7所示,表中数值包括结构响应的控制效果、AMD控制力以及行程。
当结构参数无偏差时,试验结果对比如表6所示。结构在基于区域极点配置算法的控制器的作用下,第4层有无控制的时程曲线对比如图7所示。当结构刚度、质量分别有-38.3%,16.8%的偏差时,两种系统的试验结果对比如表7所示。基于区域极点配置算法的控制器的作用下,其时程曲线对比如图8所示。
本文以上述试验系统为例,对比分析不同控制系统对结构阻尼比的影响,如表8所示。其中,试验模型原有的各阶模态阻尼比是经实测得到,根据激光位移测试系统测得自由衰减振动时钢框架各楼层位移时程曲线,再采用单自由度系统的计算方法近似计算相应各楼层的阻尼比,取其平均值为最终的阻尼比。
表6结构响应控制效果对比(δK=δM=0)
Tab.6Control effectiveness of structural responses (δK=δM=0)
控制指标经典极点配置区域极点配置位移加速度位移加速度控制第2层26.3250.9230.3456.86效果/第3层25.4246.8030.2045.23%第4层24.6360.4031.5554.55控制力/N28.6427.70行程/m0.160.17
表7结构响应控制效果对比(δK=-38.3%,δM=16.8%)
Tab.7Control effectiveness of structural responses (δK=-38.3%,δM=16.8%)
控制指标经典极点配置区域极点配置位移加速度位移加速度控制第2层9.1627.1027.5552.47效果/第3层10.5015.6629.2946.83%第4层10.8034.0235.9262.70控制力/N28.5028.63行程/m0.170.18
表8试验系统前4阶阻尼比
Tab.8The first four damping ratios of the experimental system
1阶2阶3阶4阶无控系统0.0320.0320.0320.032极点配置0.0640.0320.0320.032区域极点0.0690.0490.0370.032
从表6~8及图7和8可看出:(1)当系统出现参数不确定量时,经典极点配置控制方法的控制效果比较差,结构第4层的位移控制效果仅为10.80%,其位移、加速度控制效果分别下降了13.83%和26.38%;(2)区域极点配置控制方法较为有效,结构第4层位移、加速度控制效果分别提升了4.37%和8.15%,运用区域极点配置控制方法在结构参数具有较大偏差时,依然能够将结构的位移、加速度控制在较理想的范围内,故基于区域极点配置的控制方法有较为明显的优势;(3)由于AMD系统与结构的相互作用,而且结构水平向与竖直向振动存在着耦合作用,在正弦激励作用下,结构位移及加速度响应并不完全服从正弦变化规律;(4)由于控制加速度响应需要较高频率的控制力,而过高频率的控制力将激发结构高阶振型,结构第3层的高阶振型相位与控制器所在的第4层的相反,因此第3层的加速度控制效果与第2,4层的相比会相对较差;(5)两种控制算法均有效增大结构阻尼比,区域极点配置算法较经典极点配置算法更加合理,本文经典极点配置算法主要增加了第一阶振型阻尼比,而高柔结构的高阶振型对加速度响应也有影响,不可忽略;当结构的参数发生偏差后,虽然系统依旧保证目标阻尼比不变,但基于常规极点配置控制系统的效果下降较为明显,而基于区域极点配置控制系统的效果依旧良好,也从侧面反映了本文设计的鲁棒控制器的有效性。图7实验系统第4层响应时程对比(δK=δM=0)
Fig.7Comparison of structural responses to 4th floor of the experimental system(δK=δM=0)图8实验系統第4层响应时程对比(δK=-38.3%,δM=16.8%)
Fig.8Comparison of structural responses to 4th floor of the experimental system(δK=-38.3%,δM=16.8%)
4结论
针对AMD控制系统中存在着不确定结构参数的问题,本文基于区域极点配置算法,推导了当取得最优反馈增益时相应的线性矩阵不等式组,通过LMI工具箱求解该不等式组的最优解,完成了区域极点配置的鲁棒控制器设计,并与精确极点配置控制器作对比。最后以10层框架结构数值模型及4层框架试验模型进行了验证,得出主要结论如下:
(1)基于区域极点配置的AMD控制系统,其闭环极点将分布在期望区域内,并且该系统的主导极点将被配置到实轴(x轴)上。说明该配置过程能够考虑结构参数不确定性的影响,有效地提高系统的阻尼,而且达到了控制系统的设计要求。
(2)对于结构参数确定的控制系统,经典极点配置以及区域极点配置两种控制算法都能明显减轻系统的响应,但当AMD控制参数相当时,后者效果更好;对于结构参数不确定的控制系统,区域极点配置控制方法的控制效果较经典极点配置的更好。
(3)试验系统表明:由于AMD系统与结构的相互作用,而且结构水平向与竖直向振动存在着耦合作用,在正弦激励作用下,结构动力响应并不完全服从正弦变化规律;过高频率的控制力将激发结构高阶振型,结构第3层的高阶振型相位与控制器所在的第4层的相反,因此第3层的加速度控制效果与第2,4层的相比会相对较差。
参考文献:
[1]滕军,陈朝骏,幸厚冰,等. 考虑结构高阶振型信息的AMD低维控制器设计[J]. 振动工程学报. 2016,29(6):1048—1056.
Teng J,Chen C J,Xing H B,et al. AMD low-dimensional controller design considering structural high modes information[J]. Journal of Vibration Engineering,2016,29(6):1048—1056.
[2]Kautsky J, Nichols N K, Dooren V P. Robust pole assignment in linear state feedback control[J]. International Journal of Control, 1985, 44: 1129—1155.
[3]乔峰,滕军,幸厚冰. 基于极点配置算法的黏滞阻尼器优化设计[J]. 土木工程学报, 2012(s2): 162—167.
Qiao Feng, Teng Jun, Xing Houbing. Optimal design of viscous dampers based on the pole assignment method[J]. China Civil Engineering Journal, 2012(s2): 162—167.
[4]俞立. 鲁棒控制:线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.
Yu Li. Robust Control—Linear Matrix Inequalities Approach[M]. Beijing: Tsinghua University Press, 2002.
[5]Bai J J, Lu R Q, Liu X, et al. Fuzzy regional pole placement based on fuzzy Lyapunov functions[J]. Neurocomputing, 2015, 167: 467—473.
[6]Datta S, Chakraborty D. Feedback norm minimisation with regional pole placement[J]. International Journal of Control, 2014, 87(11): 2239—2251.
[7]Yang F W, Wang Z D, Hung Y S, et al. Mixed H2/H∞ filtering for uncertain systems with regional pole assignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(2): 438—448.
[8]Zhang S J, Wang Z D, Ding D R, et al. On design of robust fault detection filter in finite-frequency domain with regional pole assignment[J]. IEEE Transactions on Circuits and Systems Ⅱ-Express Briefs, 2017, 62(4): 382—386.
[9]胡刚,刘永清,李远清. 不确定性控制系统的成因、分类与控制策略[J]. 工业工程, 2001, 4(1): 49—52.
Hu Gang, Liu Yongqing, Li Yuanqing. The cause of formation, the classification and the control strategy for uncertainty control systems[J]. Industrial Engineering Journal, 2001, 4(1): 49—52.
[10]Xu S Y, Chen T W. Robust H∞ control for uncertain stochastic systems with state delay[J]. IEEE Transactions on Automatic Control, 2002, 47(12): 2089—2094.
[11]Xu S Y, Chen T W. H∞ output feedback control for uncertain stochastic systems with time-varying delays[J]. Automatica, 2004, 40(12): 2091—2098.
[12]Ge J H, Frank P M, Lin C F. Robust H∞ state feedback control for linear systems with state delay and parameter uncertainty[J]. Automatica, 1996, 32(8): 1183—1185.
[13]Xie L H. Output feedback H∞ control of systems with parameter uncertainty[J]. International Journal of Control, 1996, 63(4): 741—750.
[14]Haddad W M, Bernstein D S. Controller-design with regional pole constraints[J]. IEEE Transactions on Automatic Control, 1992, 37(1): 54—69.
[15]丁幼亮,李愛群. 工程结构抗震分析[M]. 北京: 高等教育出版社, 2010.
Ding Youliang, Li Aiqun. Aseismic Analysis of Engineering Structures[M]. Beijing: China Higher Education Press, 2010.
Application of state feedback control based on regional pole-assignment
method in flexible buildings
LI Zuo-hua1, CHEN Chao-jun1, TENG Jun1,2, XING Hou-bing3
(1. Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, China;
2. School of Civil Engineering, Fujian University of Technology, Fuzhou 350118, China;
3. China Construction Fourth Division Engineering Co., Ltd. South China Branch, Guangzhou 510660, China)
Abstract: The controlled buildings with an AMD system generally use simplified calculation model. As a result, uncertainties including uncertain stiffness and mass of flexible buildings inevitably exist and will affect the design accuracy of the controller. The development of the robust AMD control strategy has important theoretical value and engineering application prospect for structural vibration control in civil engineering. In this paper, a robust controller based on regional pole-assignment method is presented. In order to improve the stability of the system, the adverse influence of uncertain structural parameters on the accuracy of calculation model is considered in the calculation process of the control gain. A ten-storey frame with an AMD system is established for numerical analysis, and its control effect and AMD parameters are regarded as the indexes. The performance comparison between the proposed controller and the conventional controller based on classical pole-assignment method is carried out. The results show that the proposed method has good control effect and stable control parameters for the flexible buildings with parameter uncertainty. Finally, a single span four-storey steel experimental frame with an AMD system is taken as an example to verify the conclusions.
Key words: flexible building; AMD control system; regional pole-assignment method; linear matrix inequality; uncertain structural parameter
