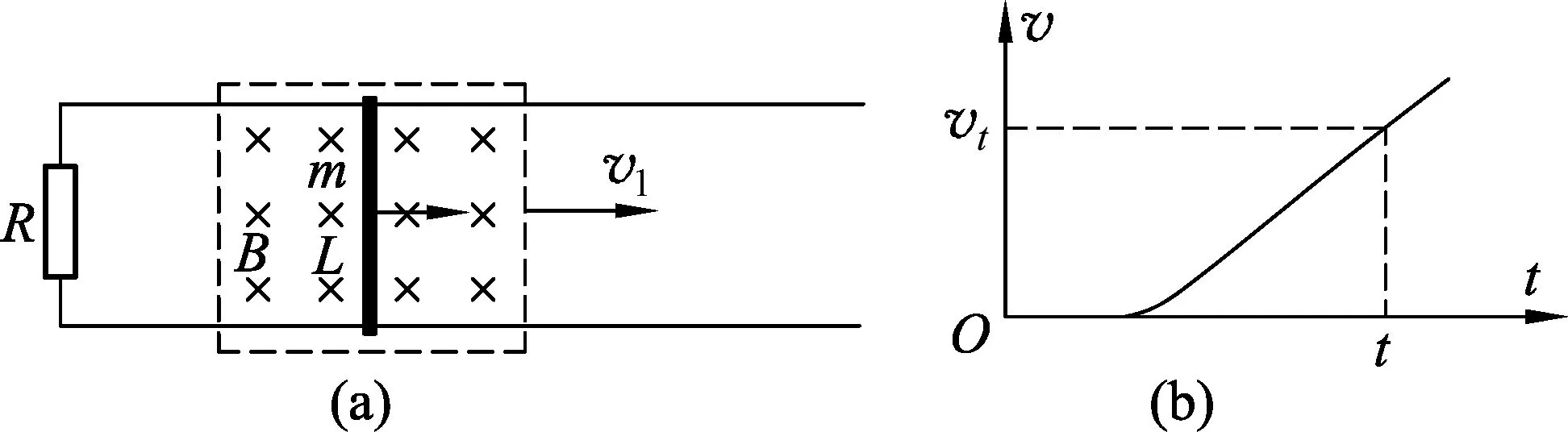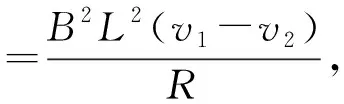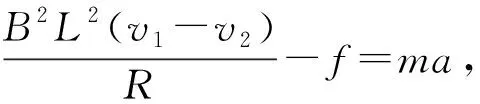“电磁感应”教学中需要澄清的几个问题
2018-06-14朱晓安张凤英
朱晓安 张凤英
(1. 北京市海淀区教师进修学校附属实验学校,北京 100097; 2. 北京市首都师范大学第二附属中学,北京 100097)
电磁感应是电磁学发展的重要内容.电磁感应现象的研究使人们从有特殊性的静电场和静磁场的静场课题,进入到变化电磁场的动力学课题.电磁感应与电场、磁场、恒定电流相比,无论是理论的抽象性还是知识的复杂性都要高一个层次,是“一种物理量对应另一种物理量的静变”研究提升到对“双向性和负反馈性同时存在的动变”研究.因此,对高中学生来说,“电磁感应”单元的学习是一个难点,从考查学生学习能力、科学素养角度看,也是各类考查命题热点和重点.
对这个单元的教学,除了要让学生理解磁通量、磁通量变化、磁通量变化率等基本概念,还要让学生通过学习“磁通量变化”去理解“电磁感应的产生条件”、学习“磁通量变化率”去理解“法拉第电磁感应定律”、学习“阻碍磁通量变化”去理解“楞次定律”.
另外,电磁感应单元教学中还需要澄清以下几个问题.
问题1.在电磁感应回路中没有感应电流,回路中是否一定没有电动势或电势差?
人教版选修3-2教材中第7页是这样描述的,“以上实验及其他事实表明:只要穿过闭合导体回路的磁通量发生变化,闭合导体回路中就有感应电流”.
能否由此推断:“如果穿过闭合导体回路的磁通量没有发生变化,闭合导体回路中就没有感应电流,回路中也就没有电动势或电势差?” 请看例1.
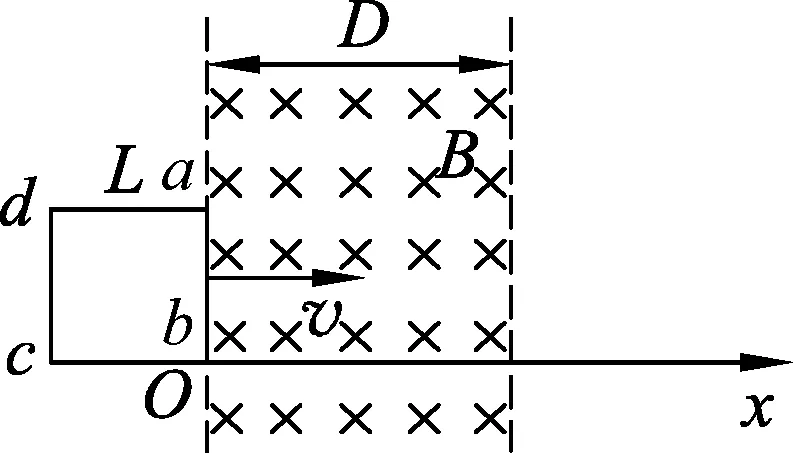
图1
例1.一正方形闭合单匝导线框abcd,边长L=0.1m,各边的电阻均为R0=0.1Ω,bc边位于x轴上且b点与坐标原点O重合.在x轴原点O的右侧有宽度D=0.2m、方向垂直纸面向里的匀强磁场区域,磁场的磁感应强度B=1.0T.当线框以v=2.0m/s的速度沿x轴正方向匀速运动穿过磁场区域.以ab边刚进入磁场时为t=0时刻,在线框通过磁场区域的过程中
(1) 画出电流I-t的关系图像(以逆时针电流为正);
(2) 画出a、b两点的电势差Uab-t的关系图像.
解析: 由题设条件可知,线框以v=2.0m/s的速度沿x轴正方向匀速运动穿过磁场区域,可以将线框的运动分成以下几个过程.
过程1:从ab边刚进入磁场到cd边刚进入磁场的过程.
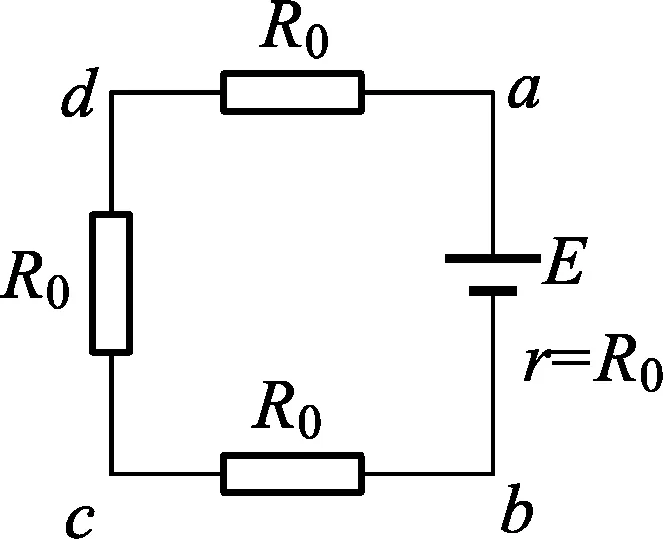
图2
此过程经历的时间为t1=L/v=0.05s,只有ab边切割磁感线,ab边相当于电源,画出等效电路如图2所示.产生感应电动势E=BLv=0.2V,回路电流I1=E/R=0.5A,电流方向沿逆时针方向,电流为正方向.
此过程ab两端电压Uab1=3I1R0=0.15V.
过程2:从cd边刚进入磁场到ab边刚离开磁场的过程.
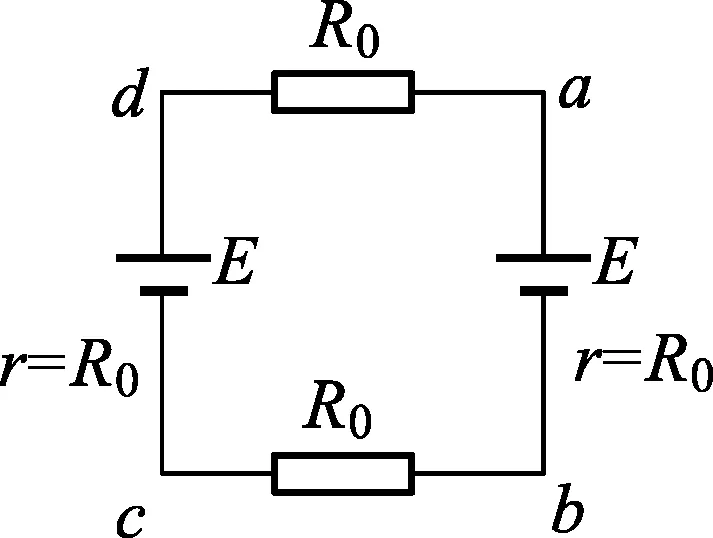
图3
此过程线框全部在磁场中,经历的时间为t2=(D-L)/v=0.05s,ab边和dc边都在切割磁感线,两边都相当于电源,画出等效电路图如图3所示.两边均产生感应电动势E=BLv=0.2V,但方向相反,所以回路电流I2=0(其实穿过闭合导体回路的磁通量没有发生变化).
此过程ab两端电压Uab2=E=0.2V.
此过程中,回路没有电流,但存在电压或电动势,且Uab=0.2V,Udc=0.2V,但Uad=0,Ubc=0.
过程3:从ab边刚离开磁场到cd边刚离开磁场的过程.

图4
此过程经历的时间为t3=L/v=0.05s,只有cd边切割磁感线,cd边相当于电源,画出等效电路如图4所示.产生感应电动势E=BLv=0.2V,回路电流I3=E/R=0.5A,电流方向沿顺时针方向,电流为负.
此过程ab两端电压Uab3=I3R0=0.05V.
由以上分析可画出3个过程中的电流I随时间变化的图像、ab两端电压Uab随时间变化的图像分别如图5(甲)、(乙)所示.
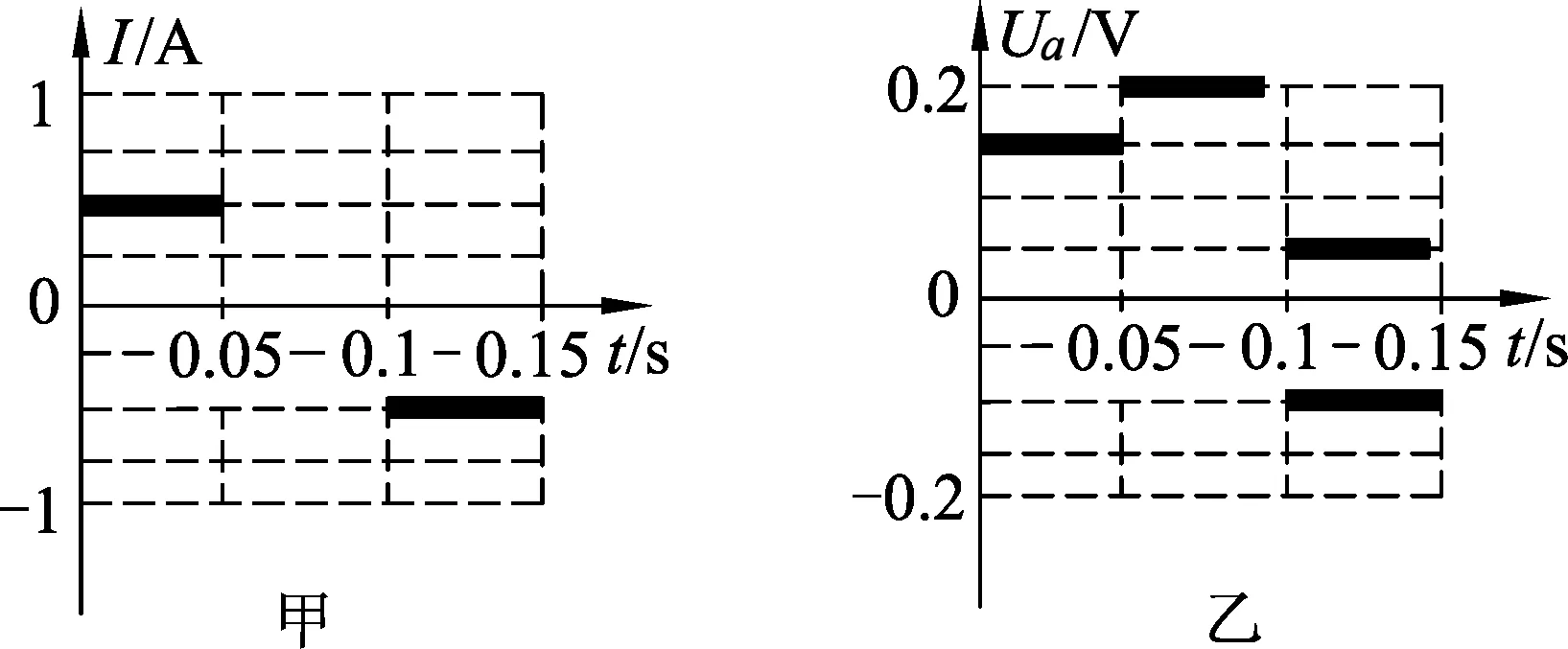
图5
小结: 通过对以上问题的分析,我们知道在过程2中,闭合回路没有电流,但回路中存在电动势,某两点之间也存在电压.因此“感应电流为0的回路就一定没有电势差或电动势”的认识是错误的.
问题2.在产生电磁感应现象的闭合回路中,能不能判别电路中各点电势的高低?
在电磁感应现象中,穿过闭合导体回路的磁通量发生变化,在闭合回路中就会产生感应电动势,形成感应电流,因此,就会有这样观点:在产生感应电流的回路中,就一定可以判断各点电势的高低.这个观点是否正确呢?请看例题2.
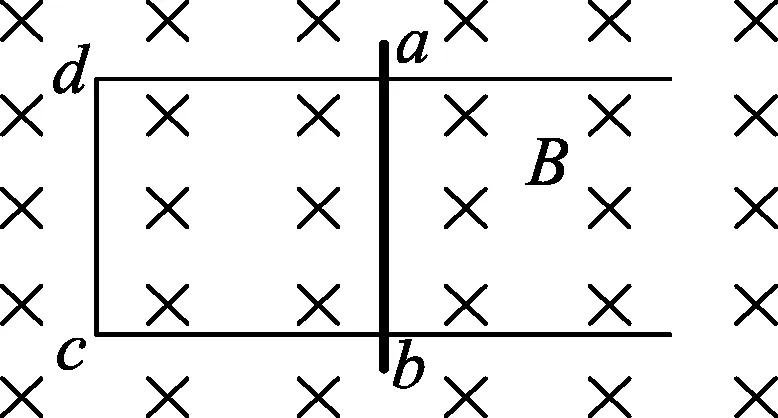
图6
例2.如图6所示,一个由金属导体组成的U型光滑轨道,轨道平面处于水平面内,有一导体杆ab放置在导轨上,与轨道垂直,杆及轨道的电阻皆不可忽略,整个装置处于匀强磁场B中,磁场方向垂直轨道面向下.
(1) 现用一外力沿轨道方向拉杆,使杆ab向右匀速运动,能否判断回路中a、b、c、d各点电势高低?如何判断?
(2) 如果保持ab杆不动, 保持磁场方向不变,只增大磁场磁感应强度,能否判断回路中a、b、c、d各点电势高低?为什么?
解析: (1) 导体杆ab向右做切割磁感线运动,产生动生电动势.根据右手定则,可以判断出ab中的电流从b→a,回路中的电流b→a→d→c,但ab杆相当于电源,因此,可以判断出各点电势φa>φd>φc>φb.
(2) 由于围成的导体回路面积不变,只是磁感应强度B增大,导致磁通量变化,产生感生电动势.根据楞次定律也可判断,回路中的电流b→a→d→c,电流方向与(1)相同,但由于感生电动势是由于B变化产生的涡旋感生电场对电荷的非静电力搬运电荷形成的,在涡旋感生电场中,感生电场对电荷做功与路径有关,不能引入电势概念,所以回路中不能判断电势高低.
小结: 通过以上分析可知,如果回路电流由感生电动势产生的,也就是通过磁场变化产生的涡旋感生电场对电荷产生的作用力推动电荷产生电动势的情况下,不能判断电路中各点电势高低;如果回路电流由动生电动势产生的,也就是闭合回路中部分导体与磁场相对运动切割磁感线,使部分导体中的自由电荷受到的洛伦兹力作用,在洛伦兹力对电荷作用搬运电荷产生电动势的情况下,就能判断电路中各点电势高低.
问题3.导体杆切割产生的感应电动势E=BLv中的v是指什么速度?
动生电动势计算公式E=BLv中速度v是导体杆(切割磁感线)的运动速度还是导体杆与磁场的相对运动速度?请看例题3.
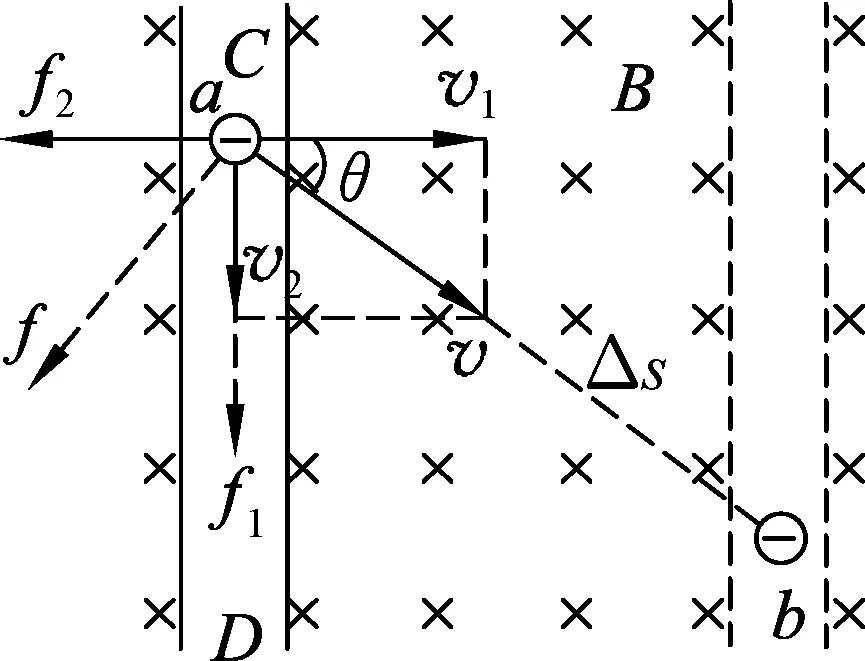
例3.如图7(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,并很快达到恒定速度.设导体棒受到水平向左、大小为f的恒定阻力,导体棒始终处于磁场区域内.
(1) 求导体棒所达到的恒定速度v2;
(2) 为使导体棒能随磁场运动,阻力最大不能超过多少?

图7

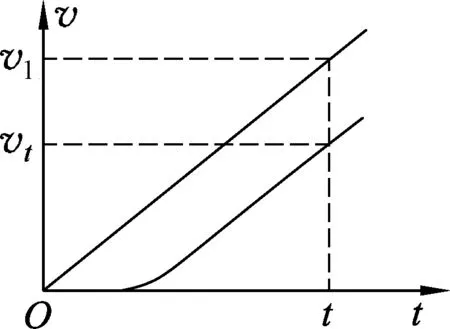
图8
解析: (1) 导体棒达到恒定速度,表明达到最大速度并且匀速运动,分析物体水平方向受力如图8所示.因此F合=0,即F安-f=0.
又F安=BIL,I=E/R,E=BLv,此处的v是什么速度呢?导体棒的切割磁感线的速度既不是v1,也不是v2,而是导体棒和磁场的相对速度v=v1-v2.如果v1=v2,则说明导体棒与磁场相对静止,不存在切割速度,因此不会产生感应电动势.
E=BL(v1-v2),
有
解得
其中v1 (2)为了使导体棒能随磁场运动,则至少有F安-f=0,根据(1)的分析有 小结: 由以上分析可以看出,在E=BLv公式中,v是导体杆与磁场的相对切割速度,不能单纯理解为导体杆的速度,如果v是导体杆的速度,这只是磁场静止状态下的一种特殊情况. 问题4.安培力对导体杆做负功(功率)的大小是不是一定等于产生的电能(电功率)? 在解决导体杆(或导线框)切割磁感线产生感应电流,回路中产生多大的电能的问题时,很多学生都认为“安培力对导体杆做的负功的大小就一定等于回路中产生的电能”,这个结论是否正确?让我们看下面的例4. 例4.如图9(a)所示,光滑的平行长直金属导轨置于水平面内,间距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上.导轨和导体棒的电阻均不计,且接触良好.在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B.开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,并很快达到恒定速度.设导体棒受到水平向左、大小为f的恒定阻力,导体棒始终处于磁场区域内. (1) 导体棒以恒定速度运动时,单位时间内克服阻力所做的功和电路中消耗的电功率各为多大? (2) 若t=0时磁场由静止开始水平向右做匀加速直线运动,经过较短时间后,导体棒也做匀加速直线运动,其v-t关系如图9(b)所示,已知在时刻t导体棒的瞬时速度大小为vt,求导体棒做匀加速直线运动时的加速度大小. 图9 电路中消耗的电功率可以有两种求法. 第1种方法:利用电功率的定义计算. 第2种方法:利用能量转化关系计算. 图10 (2) 定性作出磁场匀加速运动与导体棒匀加速运动的速度图像,如图10所示. 小结: 由以上分析可知:导体杆切割磁感线产生感应电流,在电路中产生的电能(或电功率),不一定等于安培力对导体杆所做的负功(或功率),这只是一种磁场处于静止状态下的特殊情形.如果磁场也是运动的,那么,电路中产生的电能(或电功率)一定等于安培力对导体杆与磁场组成的系统所做的总功(或总功率). 问题5.电磁感应现象中,是什么力充当非静电力搬运电荷做功,使其他形式的能转化为电能? 在电磁感应现象中,产生的感应电动势分两种,一种是动生电动势,一种的感生电动势. (1) 感生电动势. 由于磁场强弱的变化,变化的磁场在周围产生感生电场,闭合回路处于感生电场中,由感生电场产生的电动势,我们称之为感生电动势. 图11 如图11所示的空间,存在向上方向的磁场,且磁场变强,根据英国物理学家麦克斯韦的理论,变化的磁场,就会在空间激发一种电场,这种电场与静电场不同,不是由静止电荷产生的,而是由变化的磁场产生的感生电场. 如果此刻空间存在闭合导体,导体中的自由电荷就会在感生电场的作用下做定向运动,产生感应电流,或者说导体中产生了感应电动势.这种情况下,所谓的“非静电力”就是感生电场对自由电荷的作用力.感生电场对自由电荷的作用力在 “搬运”电荷过程中,对电荷做功,把磁场能转化为电能. (2) 动生电动势. 导体做切割磁感线运动,由于自由电子受到的洛伦兹力推动电荷,对电荷做功,产生的感应电动势称之为动生电动势. 图12 如图12所示,导体杆以速度v1向右做切割磁感线运动,导体内部的自由电子随导体杆以速度v1向右运动,受到磁场产生的洛伦兹力f1的作用,洛伦兹力f1在这里起着电源内部非静电力的作用. 以前曾学过,由于洛伦兹力总和电荷运动的方向垂直,所以洛伦兹力不做功.在这里又说洛伦兹力所做的功,似乎有些矛盾. 下面我们分析一下力做功的情况和能量的转化过程. 随着导体杆运动的自由电子在f1的作用下,产生加速度,就有了沿杆方向的速度v2,这个方向的速度分量也会使自由电子受到垂直于v2的洛伦兹力f2的作用,最终,自由电子运动的合速度为v,受到的洛伦兹力f,如图12所示. 其中分力f1对自由电子做正功,相当于非静电力搬运电荷做功,克服导体杆 中的电场力做功,使得回路中储存电能,储存的电能来源于导体杆减小的机械能;分力f2对自由电子做负功,所有电荷受到这个分力的总和相当于导体杆受到的安培力.这个安培力对导体棒做负功,使得导体杆的机械能减小,减小的机械能转化为导体杆中储存的电能.综合来说,洛伦兹力f并不做功,但其作用是把导体杆的机械能转化为电能,从宏观上看,就是安培力对导体杆做负功,使导体杆的机械能减小,转化为电路中的电能.因此洛伦兹力起到的是一个能量转化的中介作用. 小结: 在电磁感应现象中,如果是动生电动势,则充当“非静电力”的是洛伦兹力的一个分力,这个分力在搬运电荷的过程中对自由电荷做正功,把其他形式的能量转化为电能,洛伦兹力的另一个分力对电荷做负功,宏观上表现为安培力对导体杆做负功,总之是把机械能转化为电能的;如果是感生电动势,则充当“非静电力”的是感生的“涡旋电场”对电荷的作用力,这个力在搬运电荷的过程中是对自由电荷做正功的过程,克服导体杆中的静电场力对电荷做功,把磁场能转化为电能. 结束语: 通过以上分析,在进行电磁感应单元教学的过程中,不仅要进行基本概念、基本规律的教学,把书本上的知识传授给学生,更要通过问题讨论或辨析的方式,把这几个学生感觉模棱两可、甚至是错误的观点进行澄清.这样不仅使学生懂得了电磁感应过程中的基本规律,更让学生学会从表面现象入手,深入分析事物的本质特征,因此澄清这些问题十分有必要.