朴素贝叶斯分类法在考试管理中的应用

梅晓晴

(天津市学位与研究生教育发展中心,天津 300381)

机器学习是人工智能及模式识别领域的共同研究热点,其理论和方法已被广泛应用于解决工程应用和科学领域的复杂问题。分类算法是机器学习中的重要部分,其基本思想是首先知道大量的样本对象,并且知道这些样本对象的“特征”和所属类别,把这些数据告诉计算机,让计算机总结分类的原则,形成一个分类模型,再把新的待分类或者未知分类的样本交给它,让它完成分类过程。也就是说,先用一部分有种种特征的数据和每种数据归属的标识来训练分类模型,当训练完毕后,再让计算机用这个分类模型来区分新的没有类别标识的样本,从而完成该样本的分类。

贝叶斯分类是统计学中一种利用概率知识进行分类的方法,它可以预测一个未知类别的样本属于各个类别的可能性,并且选择其中可能性最大的一个类别作为该样本的最终类别。朴素贝叶斯算法(NBC)是简单常用的统计学分类算法[1],朴素贝叶斯分类器是在机器学习中应用最广泛的一种分类器,其分类算法包括两个过程:训练过程和测试过程[2]。在人们生产生活中,使用朴素贝叶斯分类器的思维解决问题比直接套用公式的机会多。本文通过朴素贝叶斯分类方法,探索利用已有经验数据来判断考生行为的规律,从而有针对的加强监考,提高考试管理效率。

1 贝叶斯定理

贝叶斯分类的理论基础是贝叶斯定理,贝叶斯定理将事件的先验概率与后验概率联系起来,它在后验推理、参数估计、模型检测等诸多统计机器学习领域方面有广泛而深远的应用[3]。

设 D1、D2、……、Dn为样本空间S的一个划分,如果以 P ( Di)表示 Di发生的概率,且 P ( Di)>0(i=1,2,…,n)。对于任何一个事件x,P（ x）>0,则有:

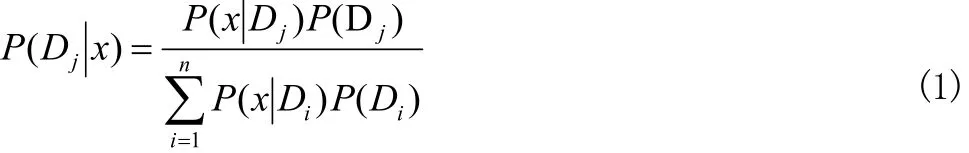
在一个样本空间里有很多事件发生, Di就是指不同的事件划分,并且用 Di可以把整个空间划分完毕,在每个 Di事件发生的同时都记录事件x的发生,并记录 Di事件发生下x发生的概率。等式右侧的分母部分就是 Di发生的概率和 Di发生时x发生的概率的加和,所以分母这一项其实就是在整个样本空间里x发生的概率。P （Djx）这一项是指x发生的情况下, Dj发生的概率。因此,左侧和右侧分母项相乘得到的是在全样本空间里,在x发生的情况下又发生 Dj的情况的概率。右侧分子部分的含义是 Dj发生的概率乘以 Dj发生的情况下又发生x的概率。

所以最后等式两边就化简为:

在全样本空间下,发生x的概率乘以在发生x的情况下发生 Dj的概率,等于发生 Dj的概率乘以在发生 Dj的情况下发生x的概率。

贝叶斯分类通常基于这样一个假定:给定目标值时属性之间相互条件独立,基于这种“朴素”的假定,贝叶斯公式一般简写为：

上式也成为朴素贝叶斯公式,P（ A）叫做A事件的先验概率,就是一般情况下,认为A发生的概率。P （ BA）叫做似然度,是A假设条件成立的情况下发生B的概率。P（ AB）叫做后验概率,在B发生的情况下发生A的概率,也就是要计算的概率。P （ B）叫做标准化常量,和A的先验概率定义类似,就是一般情况下,B的发生概率。

2 朴素贝叶斯分类器

朴素贝叶斯分类器是一个简单有效而且在实际使用中很成功的一个分类器[4]。设有变量集 U =｛X1, X2,…,Xn,C｝,其中, X1, X2,…,Xn是实例的属性变量,C是m个值的类变量。假设所有的属性都条件独立于类变量C,即每一个属性变量都以类变量作为唯一的节点,而属性变量之间是完全独立的,就会得到朴素贝叶斯模型。

使用朴素贝叶斯分类器进行分类的方法是:通过概率计算,从待分类的实例的属性值 x1, x2,… ,xn中求出最可能的分类目标值。即计算各类 cj∈C对于这组属性的条件概率P （cjx1,…, xn）,其中j=1,2,…,m,并输出条件概率最大的类标签作为目标值。应用贝叶斯定理和条件独立性假设[5]：

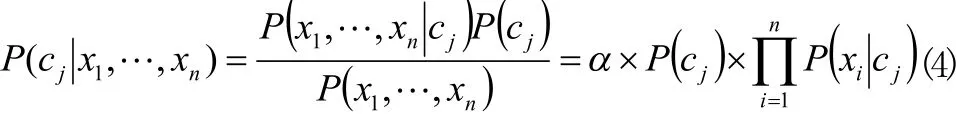
其中α是正规化常数。以后验概率作为分类指示,即输出具有最大后验概率 f（ x）。

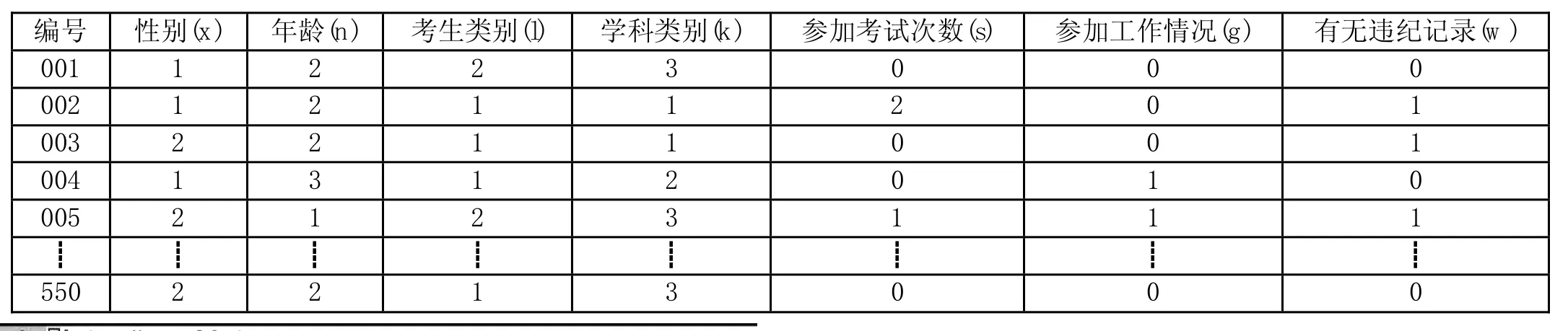
表1 训练样本集

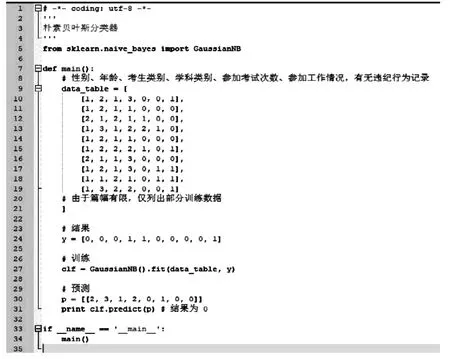
图1

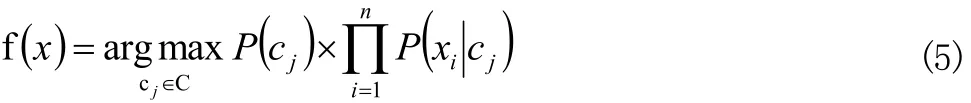
其中 f（ x）表示朴素贝叶斯网络输出的目标值,常数α可以省略。通常式(5)也作为朴素贝叶斯分类器的定义[6]。

关于 P （ cj）和P （ xicj）的求解,有以下三种常见的模型高斯模型、多项式模型、伯努利模型,当特征是连续变量的时候,运用多项式模型就会导致很多P （ xicj）=0,此时即使做平滑,所得到的条件概率也难以描述真实情况。所以处理连续的特征变量,应该采用高斯模型,即:

其中μcj表示类别为c的样本中,第j维特征的均值,σcj表示类别为c的样本中,第j维特征的方差[6]。

3 基于朴素贝叶斯分类预测考生行为

3.1 分析评价指标

数据样本用一个7维特征向量X=(x1,x2,……x7)表示,分别描述性别、年龄、考生类别、学科类别、参加考试次数、参加工作情况,有无违纪行为记录等对考生行为产生的影响。

性别(x)=(x=1男;x=2女);

年龄(n)=(n=1,年龄<18;n=2,18≤年龄<22;n=3,年龄≥22);

考生类别(l)=(l=1成人在籍本科生;l=2自考在籍本科生);

学科类别(k)=(x=1管理学,经济学;x=2工学,理学;x=3医学,教育学);

参加考试次数(s)=(s=0;s>=1);

参加工作情况(g)=(g=1已参加;g=0未参加);

有无违纪行为记录(w)=(w=1有记录;w=0无记录);

行为判断结果(p)=(p=0正常;p=1疑似异常)。

3.2 训练数据的选取

以2013-2017年间5次考试的550名考生作为训练样本数据,经过加工整理,提取出相关的数据,再对数据进行预处理,除去数据中的冗余信息。数据预处理包括处理缺失值、删除无效数据等。最后生成包含550个样本的训练样本集,如表1所示。

3.3 构建朴素贝叶斯分类模型

由于采用朴素贝叶斯分类器进行分类是一个庞大且复杂的计算过程,所以这里只根据已有条件进行简单预测。通过表1的数据,预测25岁男性成人在籍本科生,专业为管理学,参加过考试且已经工作,没有违纪记录的评估结果,即未知样本。

在Python的Scikit-learn库中,虽然对朴素贝叶斯分类算法做了实现,但是对于建模针对性的问题,分别做了几种贝叶斯分类的变种模型封装。分别是高斯朴素贝叶斯;多项式朴素贝叶斯;伯努利朴素贝叶斯。这三种训练的方式非常相近,引用时所写的代码也非常简短。其中,高斯朴素贝叶斯是利用高斯概率密度公式来进行分类拟合的。多项式朴素贝叶斯多用于高纬度向量分类,最常用的场景是文章分类。伯努利朴素贝叶斯一般是针对布尔类型特征值的向量做分类的过程。

本例使用高斯朴素贝叶斯模型,代码如图1:

从计算结果可以看出,朴素贝叶斯分类器预测样本的评估结果为“正常”,这与实际结果相同。通过分析大量评估结果数据,会发现其中起决定因素的主要是考生年龄、学科类别及工作情况,通过这种潜在联系的应用,可以为提前预测以及考试过程中判断考生行为提供合理科学的技术支持。

朴素贝叶斯分类技术在考试管理中的应用,克服了仅凭个人经验主观判断的缺点,它不再是一个简单的直接套用的公式,而是一种机器学习的思想,对它的灵活运用可以减轻监考人员压力,提高考试管理效率,相信也会在将来有更广泛的应用。

[1]郑炜,沈文,张英鹏.基于改进朴素贝叶斯算法的垃圾邮件过滤器的研究[J].西北工业大学学报,2010,28(4):622-627．

[2]张增伟,吴萍.基于朴素贝叶斯算法的改进遗传算法分类研究[J].计算机工程与设计,2012,33(2):750-753．

[3]Barber D.Bayesian Reasoning and Machine Learning[M].Cambridge:Cambridge University Press,2012.

[4]RAMONI M,SEBASTIAMI P.Robust bayes classifiers[J].Artificial Intelligence,2001,125(1/2):209-226.

[5]李晓毅,徐兆棣,孙笑微.贝叶斯网络的参数学习研[J].沈阳农业大学学报,2007,38(1):125-128.

[6]Gelman A,Carlin J,Stern H,et al. Bayesian Data–Analysis [M]Boca Raton: CRC Press,2013.

[7]王双成,杜瑞杰,刘颖.连续属性完全贝叶斯分类器的学习与优化[J].计算机学报,2012,35(10):2129-2138．