齿轮刚度对齿轮敲击力影响仿真分析

2018-06-13潘凤湖刘红旗

机电产品开发与创新 2018年3期

闾昂，潘凤湖，刘红旗

（机械科学研究总院中机生产力促进中心，北京 100044）

0 引言

汽车变速器敲击振动噪声普遍存在一直是汽车常见噪声中难以解决的棘手问题，该噪声容易使人产生疲劳和烦躁感，严重影响车辆的乘坐舒适性和产品品质，现阶段在此方面的理论研究还不完善，在理论方面[1]只是说明了敲击力与齿轮刚度k有关，而决定轮齿刚度的主要参数是齿宽B及螺旋角β，但是具体参数间内在数量关系并不明确，因此分析敲击力与决定齿轮刚度的主要参数间函数关系对完善齿轮敲击理论及降低整车噪音提高产品质量显得尤为重要。变速器敲击噪音主要发生在主动轮转速800～2000r/min区间内，本文应用ADAMS[2]对变速器空套齿轮敲击现象进行动力学仿真，并结合数据处理方法[3]对研究敲击力与齿轮参数之间的函数关系及完善齿轮敲击理论进行了有益的尝试。

1 数学模型建立与分析

1.1 敲击过程等效数学模型

仅考虑单对齿轮啮合，该单对齿啮合系统可以等效为单自由度弹簧阻尼系统，等效系统的结构如图1所示。

图1 单对齿啮合等效系统Fig.1 An equivalent system for tooth meshing

对该系统建立数学模型并形成敲击过程的动力学微分方程，数学模型及微分方程如下：

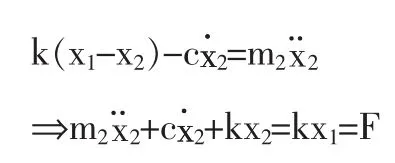
其中：

为角速度波动率

x2（t）=Re-ξωntcos（ωdt-φ）+X0sin（ωt-Φ）这里重点考虑右边第一项 Re-ξωntcos（ωdt-φ）

令 x2衰减项（t）=Re-ξωntcos（ωdt-φ），x2稳态项（t）=X0sin（ωt-Φ），ωd为系统有阻尼情况下固有角频率，ω为被迫振动固有角频率，这里阻尼系数很低使得ωd≈ωn

m2的加速度为

整理得：

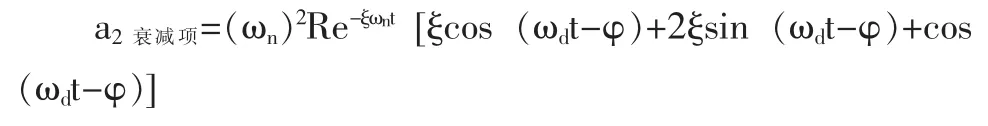
由于 ξ＜＜1，a2衰减项≈（ωn）2Re－ξωntcos（ωdt－φ），m2a2衰减项=m2（ωn）2Re－ξωnttcos（ωdt－φ）

1.2 影响刚度的主要参数分析

根据渐开线圆柱齿轮承载能力计算方法[4]，影响齿轮啮合刚度的主要参数为螺旋角β和齿宽B，单齿总刚度k=c'B可见齿轮刚度与齿宽B及单位齿宽刚度c'均成正比关系。单位齿宽c'计算公式如下：

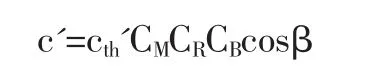
式中：cth'—单对齿刚度理论值（N/（mm·μm））；CM—理论修正系数，这里CM=0.8；CR—轮坯结构系数，这里CR=1，CB—基本齿廓系数，这里CB=0.975

其中：zn1，zn2—大小斜齿轮当量齿数。对于内啮合齿轮zn2取无限大。x1，x2—大小齿轮变位系数（这里均为0）。

—对齿轮啮合主要是等变位传动，或者正传动，此时：

f'（A）中在不发生根切的情况下 z1（min）=z2（min）=17；由于在变速器中｜x1｜，｜x2｜均小于 1，且对于正传动和等变位传动，x1＞0，x2＜0，对函数集 f'（A）当 z1（min）=z2（min）=17，x1=x2=0 时，f'（A）取到最大化曲线：f'（A）（max）此时：

f'（A）（max）为增函数，当 0.9902582358691＜A≤1 时，f'（A）（max）＞0；

f（A）（max）为增函数由于 A=cosβ，A 为 β 的减函数

当时，f'（A）max＜0（）

f（A）（max）为减函数由于 A=cosβ，A 为 β 的减函数c'为β的减函数

齿轮的刚度k随β角的增大而减小。

综上：影响齿轮刚度k的因素有两个：齿宽B与螺旋角β，变速器齿轮齿宽范围：10～30mm，螺旋角β范围：10°～30°，根据以上结论，在齿数与螺旋角不变的情况下，齿宽由10mm增加到30mm，齿宽扩大3倍，刚度k值变为原来3倍，影响显著；在齿数与齿宽不变的情况下螺旋角β由10°增加到30°，螺旋角扩大3倍，刚度k值变为原来0.945倍，影响不大，可见影响轮齿刚度的主要因素为齿宽B。可以认为刚度k∝B。由于敲击力F∝k所以本文认为敲击力F∝齿宽B。

这里做如下仿真验证：保证螺旋角β和空套齿轮转动惯量不变，主动轮转速及转速波动率不变，改变齿宽B，观察齿宽分别为15mm，18mm，20mm，22mm，25mm，28mm，30mm时敲击力F的变化。

2 模型建立

以某型汽车变速器齿轮传动系统为研究对象，利用SolidWorks[5]与geartrax建立变速器齿轮传动系统各零件的实体模型，并进行无干涉装配，建立变速器齿轮传动系统装配模型，并导入Adams中。其中主动轮及空套齿轮参数见表1。

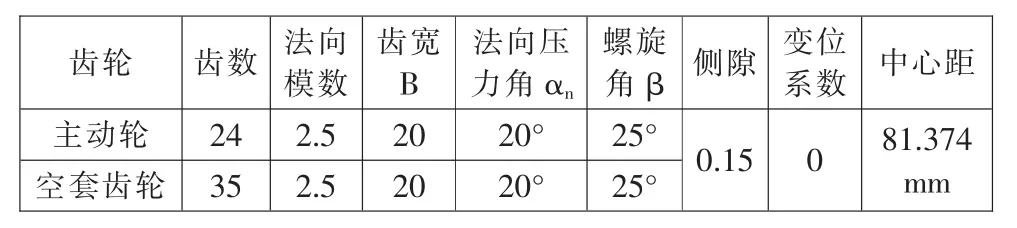
表1 齿轮参数Tab.1 The gear parameters

3 虚拟样机建立

3.1 添加约束

用铰链副定义主动轮和从动轮与变速器支撑之间的转动副，用CONTACT力定义主从动轮之间的敲击力，设置主从动轮的材料参数。虚拟样机模型见图2所示。

图2 虚拟样机模型Fig.2 Virtual prototype model

3.2 啮合力确定

齿轮敲击力用Adams中CONTACT力体现，主要确定刚度（stiffness）阻尼（damping）及刚度力指数（Force Exponent）三系数，其中刚度为材料刚度，即齿轮材料的弹性模量E （单位：Mpa），对于钢制齿轮来说，刚度（stiffness）=210000MPa；阻尼（damping）=（0.1%－1%）刚度值。对于钢铁材料刚度力指数（Force Exponent）设置为 1，Adams中 CONTACT 力具体定义如图3所示。

图3 CONTACT力定义Fig.3 The CONTACT force definition

4 仿真分析

以主动轮基本转速1500r/min，波动率5%，动力源为直列四缸发动机为例，保证空套齿轮转动惯量不变，分别改变齿宽B，观察敲击力均值F的变化，主动轮转速定义为正弦曲线，其数学形式如下：ω=ω0+ηω0sin（2ω0t）。其中：ω0为主动轮基本转速，η 为波动率。刚度k=14000000B（N/m）仿真结果见表2及图4，图5所示。