基于局部线性转换的无人机影像拼接技术
2018-06-11刘天宇赵高鹏
刘天宇,赵高鹏
(南京理工大学自动化学院,江苏南京210094)
无人机(Unmanned Aerial Vehicle,UAV)是一种获取航空影像数据的重要工具,无人机影像具有实时性强、获取方式灵活、获取成本低等优点,其应用已从最初的军事领域扩展到民用领域,在海岸监视、城市规划、资源勘查、气象观测、林业普查等众多活动中发挥着越来越重要的作用[1]。
无人机在获取影像时受到飞行高度,相机焦距以及分辨率的限制,拍摄的单张影像视野很小,仅通过一张影像无法掌握整个区域的情况,因此,如何快速获取较宽视野的无人机影像成为其应用的关键[2-3]。目前,常用的方法是基于特征点的影像拼接[4-5],即通过对无人机影像进行处理,寻找相邻图像上的同名特征点进行匹配,然后剔除相应的误匹配点,最后根据所得变换模型对影像进行无缝拼接。影像拼接中所采用的匹配算法在很大程度上影响无人机影像拼接的速度和精度。
目前国内外有许多学者对无人机影像的拼接技术进行研究。文献[6]提出一种基于扩展差分图像的拼接方法;文献[7]提出一种约束化三角剖分的拼接方法;文献[8]提出一种基于GA-SIFT和自适应阈值的拼接方法;文献[9]提出一种基于特征波段选择的拼接方法;文献[10]提出以卫星影像为底图的拼接方法;文献[11]提出一种基于单目SLAM的拼接方法。
在以上的基础上,针对无人机影像拼接累计误差大,速度慢的特点,本文在采用SURF算法[12]提取特征点后,在经过初匹配后,引入一种鲁棒的LLT局部线性转换法[13]进行误匹配点剔除,然后选取渐入渐出法对图像进行无缝拼接。最后,通过多组实验证明本文方法的有效性。
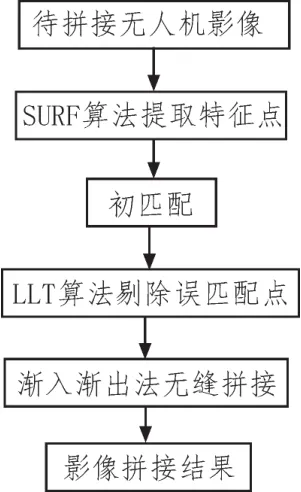
图1 算法流程图
1 基于局部线性转换的拼接算法
1.1 特征点提取
无人机在拍摄影像时,由于受到外界环境以及自身稳定性的影响,拍摄的影像可能存在平移、旋转、尺度变换等情况,因此,要求检测的特征点具有较好的鲁棒性。拼接后期随着图片的累积,特征点数目增加,因此对特征点提取速率也有很高的要求。SURF(Speeded Up Robust Features)算法由 Bay于 2006年提出,是 SIFT(Scale Invariant Feature Transform)算法的一种改进,对图像平移、旋转、尺度变换及遮挡等有较好的适应性。与SIFT算法相比,SURF实现了更快的特征提取速度。因此,本文采用SURF算法来提取特征点。
1.2 特征点匹配
通过SURF算法提取到大量特征点后,需要对影像间的同名点进行匹配。基本思路是对一张影像中的某一个特征点,采取一种搜索策略,在邻近的目标影像中作搜索,找到与之距离最近和次近的特征点,基于最邻近距离比值法(Nearest Neighbor Distance Ratio,NNDR),删除最近邻和次近邻点距离比值大于设定阈值的特征点,最终得到初步的匹配点。
由于影像间可能存在各种几何及光度变换、噪声、量化误差及相似局部结构等多种因素影响,仅仅依靠距离阈值作约束条件不可避免存在一定的错误匹配,因此需要引入其它约束对匹配结果进行提纯。目前最为流行的是RANSAC(Random Sample Con⁃sensus,随机抽样一致)算法。
但是RANSAC算法是一种不确定算法,因为算法不确定,只是由一定的概率得到一个合理的结果,为了提高这一概率,必须提高迭代的次数,大大降低了拼接的效率,在准确性和速度上无法同时达到无人机影像配准的要求。对此,文中引入了一种基于局部线性转换的提纯算法,LLT(Locally Linear Trans⁃forming,局部线性转换)算法。
LLT算法引入了一个统一的最大似然函数来估计初匹配后点集间的转换关系,引入一个变量zn∈{0,1},zn=1时匹配点正确,为0时则为误匹配点。通过EM(Expectation-Maximization,最大期望)算法[14]来估计正确的内点集,然后建立一个类似于LLE(Locally Linear Embedding,局部线性嵌入)[15-19]的局部几何约束来确保最优解的适应性。这个局部几何约束可以保存邻近特征点在转换后的几何构造特征,从而可以获得正确的匹配点。
根据文献[13],令初匹配后的N对特征点集为S={(xn,yn)}N
n=1,其中xn,yn是两个2-D列向量分别带有两幅影像上特征点的空间位置信息,X=(x1,…,xN)T和Y=(y1,…,yN)T是两个N×2 阶矩阵代表两个影像间的特征点集。为了不失一般性,假设正确匹配点的噪音是具有零均值和协方差σ2I的各向同性高斯分布,误匹配点则满足均匀分布。引入一个变量zn∈{0,1},zn=1时匹配点为正确,为0时则为误匹配点。为了得到最后的似然函数,算法引入一个参数集θ={T,σ2,γ}。T为转换方程表示图像间的几何关系,对于正确匹配点 (xn,yn),yn=T(xn)。γ表示在引入变量zn上的边缘分布(也就是任意zn,1/a表示误匹配点满足的均匀分布,a为第二张图片的面积也就是yn的范围。
考虑到无人机影像的特点,以仿射变换为模型,假设变换方程为yn=T(xn)=Axn+t,A是一个 2×2阶仿射矩阵,t是一个2×1阶转换向量,具体的算法流程如下:
其中,K是线性构造中邻近点的数量,λ是一个控制局部几何约束在转换中影响程度的参数,τ是判断匹配点是否正确的阈值。
输出:正确匹配点集Γ。
步骤1):初始化γ,A=I,t=0,P=IN×N。
其中,P=diag(p1,…,pN)为一个对角矩阵,是一个后验概率表示匹配正确的概率。
步骤2):根据方程(1)初始化σ2。
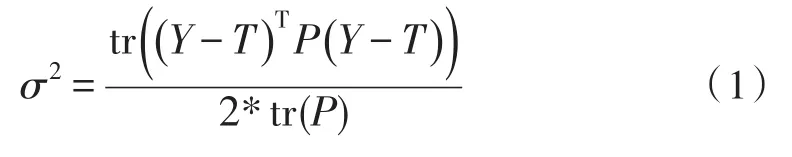
步骤3):为X中每一个特征点搜索K个邻近点。
步骤4):通过方程(2)计算W。
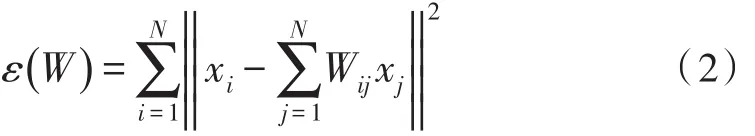
步骤5):重复迭代EM算法至收敛:
E-Step:根据方程(3)计算P
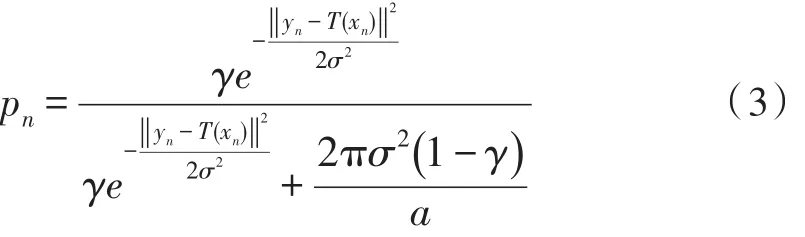
M-Step:根据方程(4)计算和
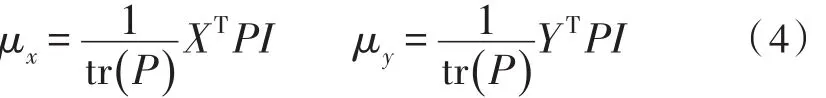
根据方程(5)(6)分别计算A和t;
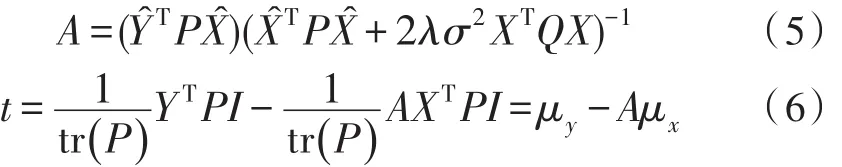
根据方程(1)(7)跟新σ2和γ;

1.3 图像无缝拼接
由于视差效应、拍摄环境变化以及配准误差等因素的影响,图像间难免会存在光照、色彩等差异。图像融合就是要消除图像光强或色彩的不连续性。它的主要思想是让图像在拼接处的光强平滑过渡以消除光强的突变。目前常见的融合算法有平均值法、多分辨率样条技术和小波变换等。本文采用一种加权融合法——渐入渐出法。
设f1,f2分别代表待融合的两幅已配准影像,f代表最后的拼接图像,则渐入渐出法的数学描述为:
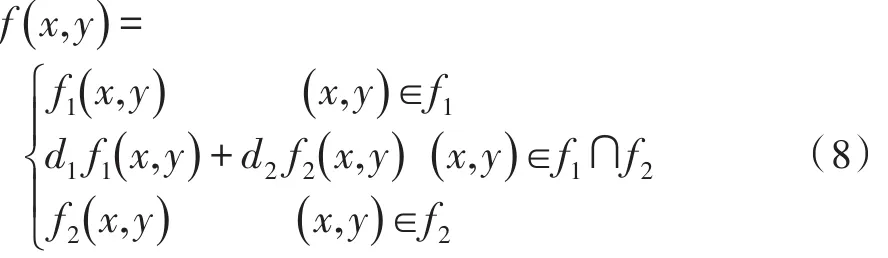
式(8)中,d1、d2分别为f1和f2的权值,通常取d=1/w,w为重叠宽度,且d1+d2=1,0 渐入渐出法在选择权值上对平均值法做出了改进,能够较好地解决图像的光照变化问题,同时算法简单直接、复杂度低、融合速度快,能够满足无人机影像拼接的需求。 综上,本文算法总体流程如图1所示。 图1 算法流程图 实验设置:文中参数设置为K=15,λ=1000,τ=0.75,初始化γ=0.9。为了验证本文方法的有效性,在MATLAB 2012b下进行仿真实验,PC配置是CPU为Intel Core i3-2350M,主频为2.30 GHz,内存为4 GB。 实验一:特征检测与匹配试验。分别用SURF+RANSAC算法和本文SURF+LLT算法对图2三组不同影像进行配准实验,其中a1,a2为一组800×800像素光照变化明显的图片,b1,b2为一组3072×2304像素旋转变化明显的图片,c1,c2为一组720×480像素缩放变化明显的图片。 我们将实验的结果以表格的形式给出,表1,表2,表3给出了不同情况下本文方法和经典RANSAC算法的对比。其中,总匹配点数是用最邻近比值法初步匹配后的结果,以RANSAC迭代次数超过4×105次后取得的匹配点作为参考标准正确值(实际操作中迭代次数过高时间过长不可取),最终匹配点数是经过RANSAC(迭代4000次)或LLT算法去除误匹配点后的结果,最终误匹配点是和假定正确匹配点做比较后不一致的匹配点数。为了尽可能检测更多的特征点来比较两个算法,在用SURF算法提取特征点时,此处将Threshold值调为0.0001,在后续的拼接实验中将改为0.002。表格中p表示绝对正确率(最终匹配正确点数/最终匹配点数)。 图2 待匹配的3组不同图片 表1 不同方法对a1,a2进行匹配结果比较 表2 不同方法对b1,b2进行匹配结果比较 表3 不同方法对c1,c2进行匹配结果比较 从表1,表2,表3中可以看出,面对不同特点的待匹配图片,尽管RANSAC算法得到的最终匹配点数比本文算法要多,但是误匹配点却有很多,绝对正确率远不如本文的算法,并且本文算法在效率上也比RANSAC要高得多。因此,在正确匹配点足够满足拼接需求时,本文算法要优于SURF+RANSAC算法。 实验二:两幅图像拼接实验。利用本文提出的方法对图3(a)和图3(b)进行无缝拼接,两幅图为1024×683像素,图4(a)和图4(b)分别为本文算法初匹配结果和最终匹配结果图,图5为最终的拼接结果图。 图3 待拼接图像 图4 图像匹配 图5 两幅图像拼接结果 可以看出,本文方法可以很好地完成两幅图像的拼接。 实验三:实拍无人机影像拼接实验。利用本文提出的方法,对一组实拍无人机影像进行拼接实验,图片像素大小均为1920×1080,图6为最终的拼接结果图片。 图6 拼接结果图 可以看出,本文方法可以很好地完成多幅无人机影像的拼接。 本文根据无人机影像的特点,通过SURF算法提取特征点,经过初匹配后,选取一种基于局部线性转换的LLT算法剔除误匹配点,最后通过渐入渐出法完成对影像的无缝拼接。通过对3组具有不同特点的图像进行匹配,将其和经典的RANSAC算法进行对比,发现本文提出的方法在绝对准确率和匹配速度上均要明显优于SURF+RANSAC算法,后续的拼接实验证明本文算法可以完成良好的图像拼接,最后的实拍无人机影像拼接实验更是证明本文的方法可以用来对大量的无人机影像进行拼接处理且具有良好的效果。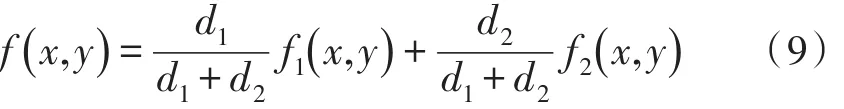
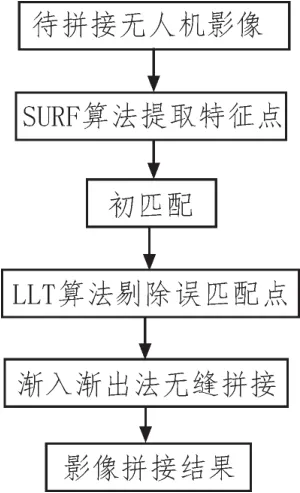
2 实验结果与分析





3 结论
