一种单目相机标定算法研究

赫美琳，高明慧，李 爽，杨开伟

（1.中国人民解放军92941部队，葫芦岛 125001；2.海军航空大学，烟台 264001；3.中国电子科技集团公司第54研究所，石家庄 050081；4.卫星导航系统与装备技术国家重点实验室，石家庄 050081）

1 引言

相机标定即计算相机内部参数的过程。相机标定的常用方法可以分为两类：传统相机标定方法和相机自标定法。传统相机标定法有直接线性变换法、两步法、张正友标定法等，近几年又提出了基于神经网络、粒子群、遗传算法的相机标定算法。相机自标定法，由Faugeras和Maybank等于20世纪90代提出，一般应用在相机的焦距等内部参数需要经常调整或相机的位姿经常变化的情况下，每对相机做一次调整，都必须对相机的内外参数进行重新标定，应用的场合主要有：主动视觉系统和移动机器人视觉系统等，因为在这些应用场景中放置标定参照物是不现实的，因此在这种应用背景下就必须采用一种不需要标准参照物的相机标定方法。相机自标定方法，不需要标准参照物，仅利用相机在运动过程中的图像序列就可以完成相机内外参数的计算。

针对传统的相机标定过程复杂、对标定参照物精度要求高等问题，本文介绍了一种简单快速的相机标定方法，具有流程简单、准确率高、算法鲁棒性强的优点。

2 相机成像模型

2.1 相机坐标系转换

像素坐标系是以像素为单位建立的坐标系，图像坐标系是以物理单位而建立的坐标系。像素坐标系和图像坐标系如图1所示：

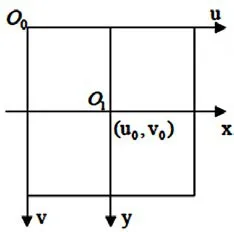
图1中，像素坐标系的原点为图像中的O0点，坐标轴为u轴和v轴，像素的坐标（u，v）代表该像素位于图像矩阵中的第u行、第v列。图像坐标系的原点为图像中O1点，原点O1为相机光心，即相机光轴与成像平面的交点。图像坐标系坐标轴为x轴、y轴，分别平行于像素坐标系的坐标轴。

图像坐标系原点O1在像素坐标系中的坐标为（u0，v0），像素的物理尺寸大小为dx，dy，则像素在两个坐标系下的转换关系为：

相机的成像几何关系如图2所示：

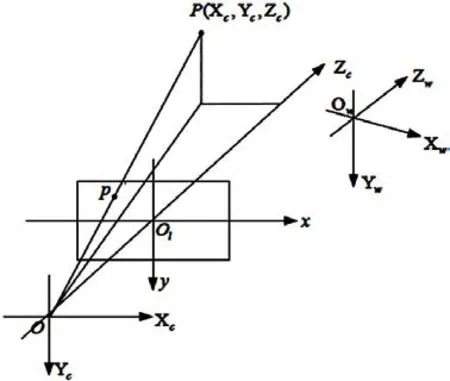
图2 相机的成像几何关系

其中，点O为相机光心；OO1为相机焦距f；点O1为图像坐标系的原点。相机坐标系原点为点O，坐标轴为Xc，Yc，Zc轴，坐标轴Xc和Yc分别与图像坐标系中的x轴、y轴平行，Zc轴为相机的光轴。世界坐标系原点为Ow，坐标轴为图中的Xw，Yw，Zw轴，相机可以安放在室内环境中的任何位置，所以相机坐标系是随相机位姿变化而变化的，因此需要设置世界坐标系。

假设空间中存在一点P，在相机坐标下的坐标为（Xc，Yc，Zc，1）T，在世界坐标下的坐标为（Xw，Yw，Zw，1）T，则两个坐标系之间的转换关系如式（4）所示：

式中，R为3*3旋转矩阵；t为3*1平移向量；0=[0 0 0]T；M1为R，t组成的4*4矩阵，为相机坐标系与世界坐标系的转换矩阵。

2.2 相机针孔成像模型

在忽略相机畸变的条件下，相机的成像模型近似为针孔模型，即空间中任意一点P在图像上的投影位置为点p，即相机光心O与P点的连线OP与图像平面的交点（如图2所示）。比例关系如式（5）：

式中，（x，y）为投影点p在图像坐标系下的坐标；（Xc，Yc，Zc）为空间点P在相机坐标系下的坐标；f为相机焦距。上述关

式中，；M为3*4矩阵，称为投影矩阵；M1由决定，只与相机内部结构相关，为相机内部参数；M2由R，t决定，R，t代表相机在世界坐标系中的位姿，为相机外部参数。

2.3 相机的畸变参数

由于针孔成像模型忽略了相机的畸变，因此不能准确地描述相机的成像几何关系。相机畸变包含三种类型：径向畸变产生的原因是成像平面与透镜平面不严格平行，它造成的不利影响有两种，一种是枕型效应，一种是桶型效应，在图像中表现为远离中心位置的图像部分会存在一定程度的畸变；切向畸变是由于透镜与成像平面不严格平行造成的；薄棱镜畸变是透镜制造过程中存在缺陷造成的。相机的径向和切向畸变如图3所示。

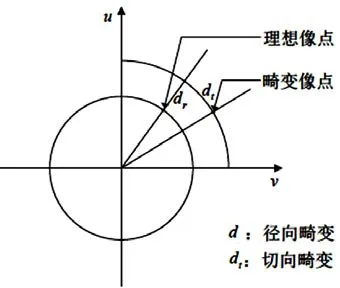
图3 相机的径向和切向畸变

采用下列公式描述相机的非线性畸变：

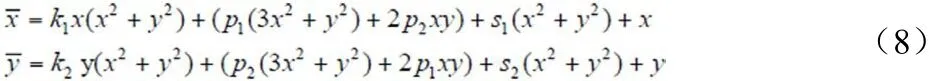
式中，为按照针孔成像模型计算出的投影点p在图像坐标系下的坐标；x，y为投影点p在图像坐标系下的真实坐标；等式右边第一项为径向畸变，第二项为切向畸变，第三项为薄棱镜畸变，各项的系数k1，k2，p1，p2，s1，s2称为非线性畸变参数。

一般情况下，描述相机的非线性畸变只需要考虑等式（8）中的第一项径向畸变。如果只考虑径向畸变，等式（8）表示为：

式中，r2=x2+y2。该式表明x方向和y方向的径向畸变大小与半径的平方成正比，即越远离图像中心畸变越大。参数和畸变参数k1，k2，p1，p2，s1，s2构成非线性模型的相机内部参数。

由上述相机成像过程得到三维空间中任意一点与其投影在图像上的点之间的对应关系，相机成像过程示意图如图4所示：

图4 相机成像过程示意图

3 相机标定

本文方法利用多幅不同位置和角度拍摄的平面棋盘格图像求解相机内外参数。该标定法的过程可以分成两步：第一步，采用针孔成像模型，建立线性方程组，求解相机内、外参数的初始值，然后以该参数作为初始值，采用最大似然进行非线性优化；第二步，考虑相机的径向畸变，采用非线性模型求解相机内外参数。具体实现步骤如下：

假设已知空间一点P的世界坐标为，对应的投影点P在像素坐标系下的坐标为P=（u，v）T，它们对应的齐次坐标分别为和=（u，v）T，空间点P和投影点P的映射关系如式（10）：

式中，s为比例因子；R、t分别为旋转矩阵和平移向量；A为相机内参矩阵，即

式中，fu，fv为图像横纵坐标轴的尺度因子即焦距与像素宽和高的比值；（u0，v0）为相机光轴与图像平面交点的坐标。

用ri表示旋转矩阵R的第i列，因为采用平面棋盘格进行标定，所以所有的空间参考点的Zw=0，由此式（12）还可以表示为：

利用最小二乘法求解式（14）可得h，进而得到单应性矩阵H的大小，按这种方法求得的单应性矩阵H与真正的单应性矩阵之间存在比例因子λ，设H=[h1h2h3]，则有：

单应性矩阵H中包含相机的内外参数，通过单应性矩阵求解出相机的内外参数。将单应性矩阵中分解得到相机的内外参数，设矩阵B满足下列条件：

求得相机内参数矩阵参数，利用内参矩阵A来确定相对于每幅图像的外参数，即旋转矩阵R和平移向量t：

设每幅棋盘格图像中包含W个标定参考点，每个标定点的坐标受到相同的噪声干扰，噪声满足独立同分布，利用最大似然估计对上述计算结果进一步优化，建立如下目标函数：

式中，Pij为三维空间中第i个参考点在第j幅图像上的投影点的坐标；Ri，ti分别为第i幅图像的旋转矩阵和平移向量；Pi为空间中第i个参考点在世界坐标系下的三维坐标；为投影点由相机内外参数计算得到的图像坐标系下的二维坐标。通过目标函数（26）的将相机标定参数求解问题转化为非线性优化问题，使目标函数最小的A，R，t即该问题的最优解。将由方程组（25）求得的结果作为初始值，然后通过牛顿法、高斯牛顿法或Levenberg-Marquarant法进行求解。

针对相机成像过程中存在的镜头畸变问题，在计算相机内外参数的公式中加入镜头的一阶和二阶径向畸变，并假设相机镜头在X轴方向与Y轴方向的畸变系数相同。设径向畸变的畸变模型为：

求得相机的一级径向畸变和二级径向畸变系数k1，k2，利用已经求出内外参，重新利用L-M算法迭代进行最小化处理，进一步优化所有的参数，得到最终相机的内部参数和畸变系数。

4 系统实验及结果分析

实验平台为：Inter（R）Core（TM）i5-4460 CPU，主频：3.20 GHz，内存大小：8.00 GB。

4.1 实验数据集

实验选用苹果电脑一体机Isight 摄像头，分辨率大小设置为320×240。标准标定参照物分为三类：三维、虚拟三维和二维。三维标定物一般用于高精度的标定，但存在制造复杂成本高的缺点。虚拟三维标定物是按照已知的移动方式移动二维标定物来模拟三维场景，其不足是需要使用高精度运动平台来实现，标定过程复杂成本高昂。本论文采用二维标定参照物，即使用A4纸打印的黑白相间的棋盘格，棋盘格数为7×10，每个方格的大小为19mm×19mm，如图5所示：

影响相机定标结果的准确性和稳定性的因素除标定算法本身外还有操作过程引入的误差，主要有三类：标定棋盘所在平面与成像平面间的夹角；标定时拍摄的棋盘格图像的数目；手动提取图像上的角点时存在误差。为了减小操作过程引入的误差，在实际标定过程中，共拍摄16幅棋盘图像，每拍摄一次就要调整一次标定板的位姿，使每幅图像拍摄的角度和距离各不相同，如图6所示：

图5 棋盘格图像

图6 相机标定图像

4.2 实验结果及分析

相机与棋盘格之间的位置关系如图7所示。

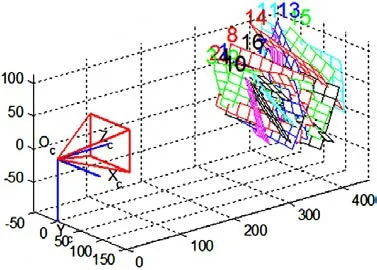
图7 相机与棋盘格的位置关系

从图8中可知，同一颜色的小十字表示同一幅标定板图像，x轴和y表示误差，单位为像素。距离坐标原点（0，0）越近的点，误差越小，反之，越大。实验表明，最终得到的参数精度较高。

相机内参标定结果如表1所示：

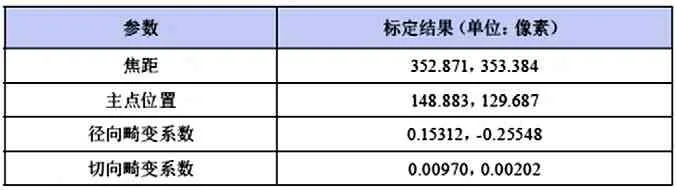
表1 相机内部参数标定结果

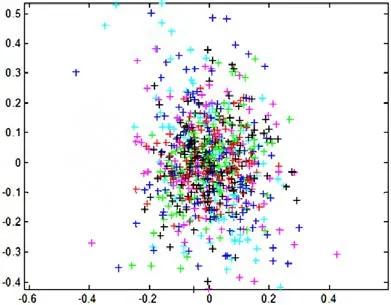
图8 重投影误差图

5 结束语

本文对基于棋盘格的相机标定法进行深入研究，详细阐述了方法的理论原理，分析了相机参数模型，并进行相机的参数标定实验，通过对实验结果的分析表明该方法具有步骤简单、精度较高的优势。下一步准备开展基于双目的相机标定算方法研究。

[1] 高宏伟.计算机双目立体视觉[M].北京：电子工业出版社，2012：95-99.

[2] 马颂德，张正友.计算机视觉-计算理论与算法基础[M].北京：科学出版社，2003：17-39.

[3] 郭静，吴怀宇，杜钊君.一种基于OpenCV的简单摄像机标定方法[J].信息技术，2011（12）：113-116.

[4] M Pollefeys，R Koch.Self-calibration and metric rexonstruction inspite of varying and unknown intrinsic camera parameters[J].International Journal of Computer Vision，1990，32（1）：7-25.

[5] Zhang Z.Flexible camera calibration by viewing a plane from unknown orientations[C].ICCV，1999：666-673.

[6] 李莉.OpenCV耦合改进张正友算法的相机标定算法[J].轻工机械，2015，33（4）：60-63.

[7] Zhang.A fl exible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligen ce，2000，22（11）：1330-1334.