基于Hyper Mesh二次开发的对接接头焊接网格过渡方法
2018-06-08张立平张红芳周鹏翔
肖 云,张立平,张红芳,周鹏翔
(1.徐州徐工随车起重机有限公司,江苏徐州221004;2.江苏徐州工程机械研究院,江苏徐州221004;3.徐工集团工程机械有限公司高端工程机械智能制造国家重点实验室,江苏 徐州 221004)
0 前言
有限元分析等数值模拟技术已成为预测温度场及应力应变场及变形行为、优化焊接顺序的有效手段之一[1]。但是焊接过程的有限元计算复杂、求解耗时长、计算效率低成为亟待解决的关键问题[2]。为了精确地反映出焊接区域的大温度梯度及大应力梯度的变化情况,需要将焊缝处的网格尺寸控制在约2mm[3]。对大型结构件而言,三维网格的自由度数目过大已经成为导致其计算效率低的关键问题之一。网格过渡技术是降低网格模型自由度数目的主要方法之一。
国内外学者深入研究自动网格划分及网格过渡,提高了网格划分的效率[4]。依据网格过渡模板,利用TCL/TK语言对Hyper Mesh软件进行二次开发,编制对接接头过渡算法,并对比不同网格过渡形式对网格质量的影响。该方法显著降低了网格划分的难度,为大型结构焊接变形预测的网格划分奠定基础。
1 网格过渡算法及质量评价
1.1 网格过渡算法
为保证模型的计算精度,母材网格划分为2~3层。在此主要介绍二维网格的过渡形式。为了保证网格的质量及其美观性,采用规则性网格过渡策略。常见的规则性网格过渡方式主要有B ias、1∶2、1∶3三种网格过渡形式[5]。二维形式的网格过渡模板如图1所示。
Bias网格过渡形式如图1b所示,细密网格和稀疏网格的单元密度不发生变化,变化主要体现在单元尺寸上;1∶2的网格过渡形式如图1c所示,细密网格的单元密度是稀疏网格单元密度的2倍;1∶3的网格过渡形式如图1d所示,细密网格的单元密度是稀疏网格单元密度的3倍。
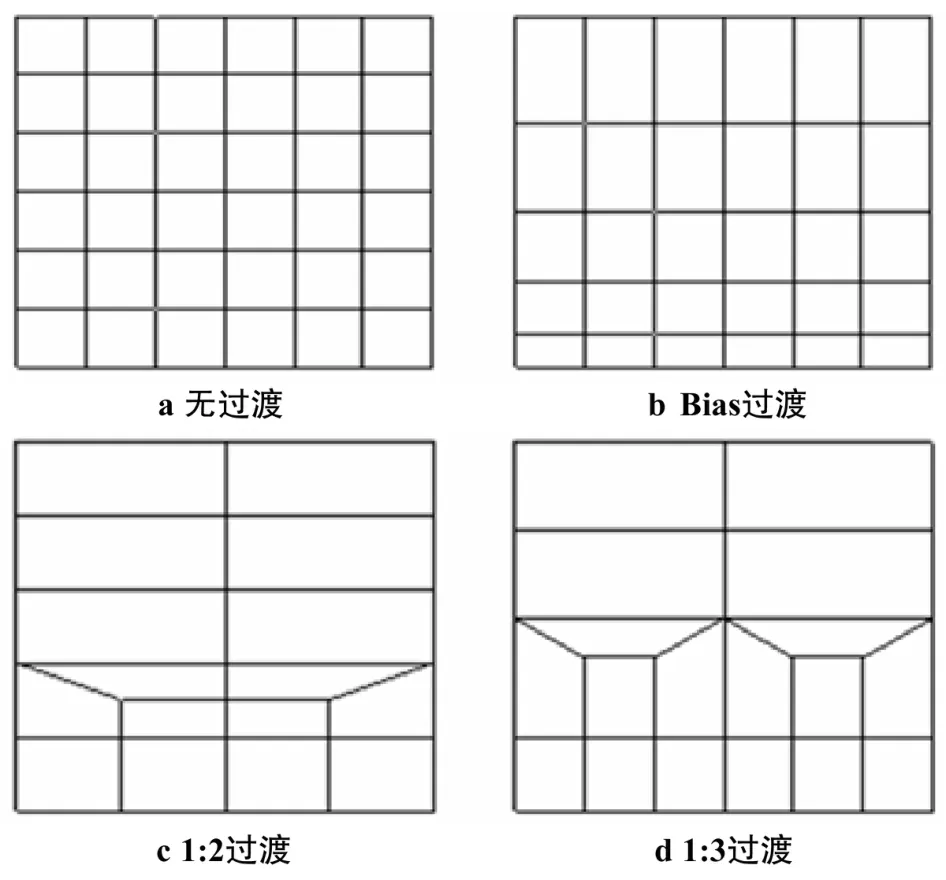
图1 二维网格过渡模板Fig.1 Patterns of 2D mesh transition
1.2 网格质量评价
模型网格离散的质量直接影响到最终计算分析的收敛性和结果精度,而这一切都依赖于有限元网格生成技术,尤其是过渡技术。由于焊接热过程的高度非线性,焊接有限元模型对网格离散密度与网格质量具有更高的要求。根据焊缝处的网格尺寸及Hyper Mesh软件中常用的网格质量检测选项,在网格划分过程中,四变形二维网格常用的质量检查选项为 min size、max size、aspect ratio、min angle、max angle及Jacobin。
2 算法开发及程序编制
2.1 算法开发
典型的V型坡口对接接头的二维截面如图2所示。由于模型的对称性,采用1/2进行网格划分,通过复制镜像的方式完成整个对接接头网格的建立。典型焊接接头主要由焊缝、熔合区、热影响区及母材组成。焊缝、熔合区、热影响区采用细密网格,母材位置采用稀疏网格。根据网格尺寸大小将几何模型分为3个区域:
(1)细密网格区——焊缝金属填充区域①、热源高非线性作用区域Ⅰ。热源高非线性作用区域的宽度a1为max(母材厚度b=9mm)。
(2)网格过渡区域——区域Ⅱ。区域Ⅱ的尺寸主要由网格的尺寸及过渡形式决定,采用Bias网格过渡形式时,无区域Ⅱ;采用1∶2网格过渡形式时,区域Ⅱ的尺寸为网格尺寸;采用1∶3网格过渡形式时,区域Ⅱ的尺寸为网格尺寸的1.5倍。
(3)稀疏网格区——区域Ⅲ。在该位置采用稀疏网格,根据尺寸需要可进行多次过渡。
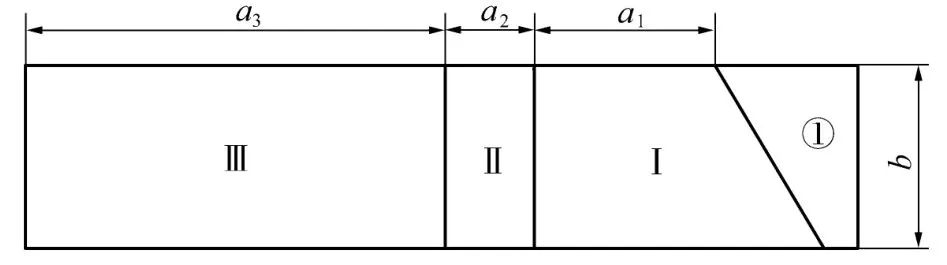
图2 对接接头网格区域Fig.2 Butt jointmesh area
2.2 程序编制
基于上述分析及网格区域划分,以TCL/TK语言为媒介,对HyperMesh进行二次开发,并将TCL/TK命令文件在Hyper Mesh中定义为宏按钮,以便程序的调用,形成如图3所示的程序开发界面,软件的执行过程如图4所示。
预估模型的自由度数目,选择相应的过渡方法,完成过渡区域及母材区域的网格划分,通过读取过渡区域的网格密度信息并选取焊缝的截面形式切割曲面,完成焊缝区及热影响区的网格划分。通过对网格进行分组及节点合并等操作,完成网格的划分。
3 应用实例
3.1 物理模型建立
2块尺寸为150mm×400mm×5mm、开V型坡口的平板进行对接焊,几何模型如图5所示。
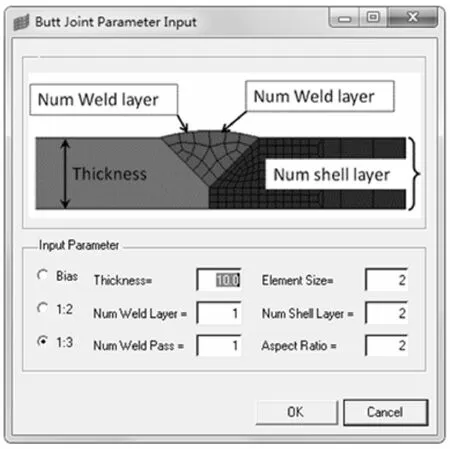
图3 参数输入界面Fig.3 Parameter input interface

图4 软件计算流程Fig.4 Flow diagram of the software
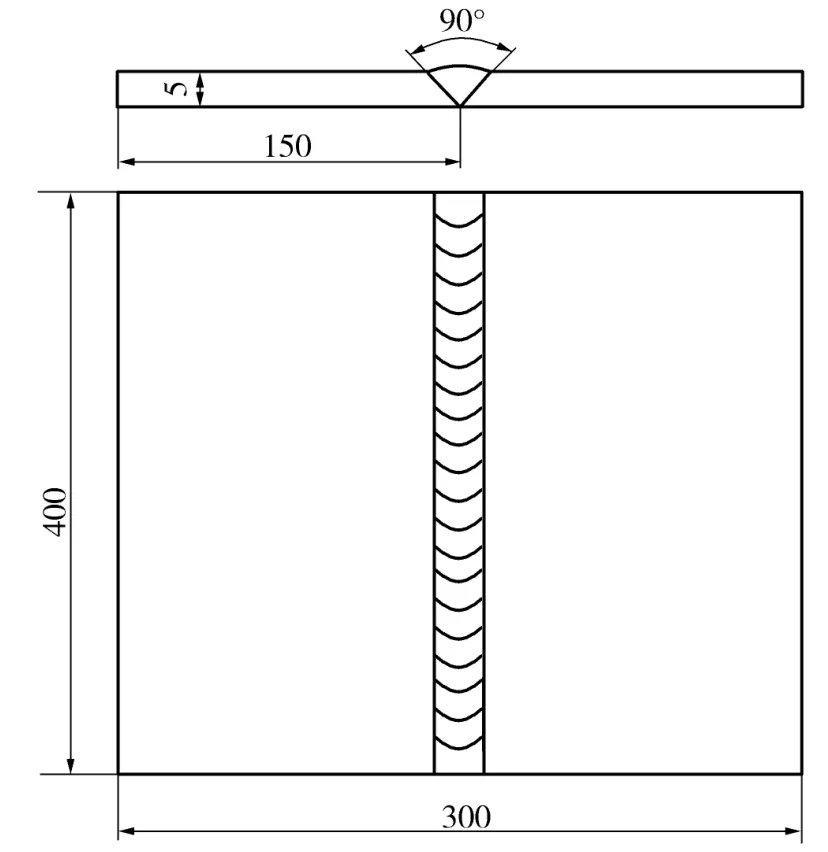
图5 平板对接焊几何模型Fig.5 Geometricalmodel of butt plate
3.2 网格模型建立
在HyperMesh中导入已建立好的三维模型,输入模型的几何参数,并采用3种网格过渡形式对几何模型进行网格划分。划分好的网格如图6所示。网格尺寸为2mm,aspect ratio为2,即模型长度方向的网格尺寸为4mm。考虑到模型的网格质量,Bias采用线性过渡,系数为3。各种方法过渡的次数均为1次。
3.3 网格模型分析
针对该模型,分别采用网格是否进行自动划分进行对比,划分时间对比如表1所示,网格划分的时间可降低60%~70%,减少了网格划分的工作量。
采用不同的过渡形式划分网格,网格数量对比如表2所示。由表2可知,采用Bias过渡方式的网格数量最多,主要原因是Bias过渡方式不能降低网格在模型长度方向上的密度,只能在单方向上调整模型的单元尺寸;与1∶3的网格过渡相比,1∶2的网格过渡较慢,因为其单元数较多。
网格质量是影响仿真精度的关键因素之一,采用不同的过渡方式的网格质量分别如表3、表4所示。由表3可知,Bias过渡网格为正方形或长方形,因此网格质量最好。1∶2过渡时,过渡区的尺寸为网格尺寸,其aspect ratio较1∶3过渡小,网格质量好。而1∶3过渡速度快,网格质量略差。由表4可知,各种过渡方式的Jacobin数值相同且网格质量较二维网格有所下降,其主要原因是焊缝的网格为五面体。
4 结论
(1)通过采用TCL/TK语言,依据网格划分模板开发网格自动划分程序,使对接接头网格划分时间降低70%,有效提高了计算分析效率。

图6 对接接头网格模型Fig.6 Buttjointmeshmodel
(2)焊缝及热影响区采用相同的网格尺寸时,对比不同的过渡类型可知,1∶3过渡网格数量最少。Bias过渡方式网格数最多,是1∶2过渡网格数的2.5倍,是1∶3过渡网格数的3.8倍。
(3)对比不同过渡形式的2D单元及3D单元可知,1∶3过渡时,aspectratio最大,而Bias过渡方式aspectratio最小。Bias过渡的网格质量最好,1∶3过渡网格质量略差。
(4)对比不同的单元过渡形式可知,1∶3 和 1∶2过渡由于过渡速度快,网格数量少,适用于大型结构件的焊接变形计算,Bias网格质量较好,适用于小构件焊接变形的精确计算。

表1 划分时间对比分析Table1 Meshedtimeanalysis

表2 网格数量对比分析Table2 Numberofmeshanalysis
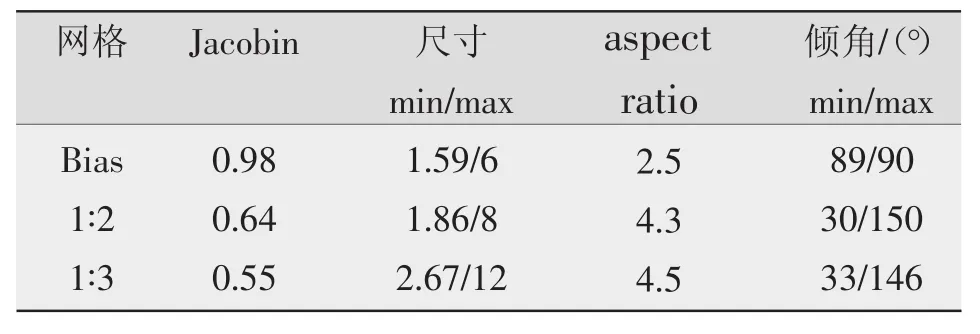
表3 2D过渡网格质量对比分析Table3 Analysisof2Dmeshtransitionquality
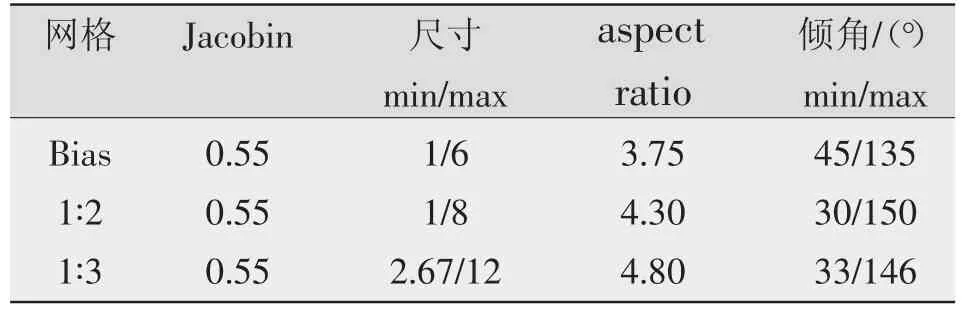
表4 3D网格质量对比分析Table4 Analysisof3Dmeshtransitionquality
[1]宋丽平.有关焊接有限元数值模拟计算前处理技术的探讨[J].热加工工艺,2012,41(9):178-180.
[2]张建勋,刘川.焊接应力变形有限元计算及其工程应用[M].北京:科学出版社,2015.
[3]陈俊梅,陆皓,汪建华,等.网格尺寸对别克轿车副车架总成焊接变形预测精度的影响[J].焊接学报,2002,23(2):33-39.
[4]米高阳,魏艳红,占小红,等.平板焊接有限元分析过渡型网格自动生成技术分析[J].焊接学报,2015,36(5):44-46.
[5]申刚.基于典型焊接构件模型的有限元六面体网格自动划分算法研究[D].江苏:南京航空航天大学,2013.
[6]AltairInc.HyperWorksRelease11.0Documentation,HyperMesh[R].2012.
