基于多图像非局部均值去噪算法研究

陈银星，商丽娟



基于多图像非局部均值去噪算法研究

陈银星，商丽娟

（五邑大学 信息工程学院，广东 江门 529000）

为提升图像去噪效果，本文提出一种基于多图像非局部均值去噪方法：首先利用多幅噪声图像线性加权并结合多图像非局部均值滤波获得预去噪图像和方法噪声；然后利用高斯滤波后的方法噪声与预去噪图像求解多图像非局部均值权值，结合权值与输入图像获得最终去噪图像. 实验结果表明，针对高斯噪声图像，与NLM等单图像去噪方法相比，本文方法能获得的峰值信噪比能提升0～2 dB，有效改善了视觉效果.

多图像去噪；方法噪声；非局部均值；高斯滤波

图像去噪是图像处理领域最基本也是十分重要一步，去噪效果好坏直接影响图像后期处理能否顺利进行，如目标识别、边缘检测等[1]. 非局部均值滤波方法（Non-local means，NLM）因去噪效果好而被广泛研究. 2005年Buades等人提取非局部均值滤波方法[2]，其方法为以参考图像块为中心设定搜索窗口并在窗口内寻找与参考图像块的相似图像块，然后对所有相似块加权平均求和获得参考图像块去噪结果. 随后，基于非局部均值滤波提出了许多去噪方法，文献[3]提出了基于概率块权值函数，对噪声图像块和迭代滤波块使用一种数据驱动方式更新权值. 文献[4]使用Stein无偏风险估计控制图像去噪的均方误差（Mean Square Error，MSE），从而为权函数的指数核选择最优平滑因子. 文献[5]对搜索窗口大小和参考块权重参数选择进行讨论，实际上是通过改善噪声图像中的像素权重求解来限制图像去噪质量. 上述方法均是通过控制权值改善图像去噪效果，也都是属于单图像去噪，所以去噪效果有限. 文献[6]认为单图像去噪效果有局限，未来难以有较大的改善.

近年来，多图像去噪方法也成为研究热点，因其可用信息多，去噪效果更好，目前已被应用于连拍图像、视频图像以及多视角图像等[7-9]. 文献[10]提出的方法分为两步：第一步利用传统NLM方法对输入噪声图像进行滤波，获得预去噪图像与方法噪声；第二步利用预去噪图像、均值滤波后的方法噪声计算像素权值，最后利用该权值对预去噪图像进行滤波获得去噪图像. 该方法优点在于第二步结合了方法噪声估计权值. 不足之一是该方法采用单图像去噪方法，计算权值的信息有限，约束了去噪效果提升；二是没有考虑高斯噪声的特性，采用均值滤波未能很好抑制噪声. 针对以上两点不足，为能更好去除图像噪声，本文在文献[10]的基础上提出了一种基于多图像非局部均值去噪方法，对方法噪声采用高斯滤波，然后联合预去噪图像求解像素权值，利用非局部均值滤波获得最终去噪图像.

1 理论基础

通常，噪声图像被模型化为清晰图像与噪声信号线性叠加

其中，是噪声图像块，是清晰图像块，是噪声信号. 图像去噪是将噪声信号从噪声图像里分离出以获得清晰图像. 本文主要研究如何去除图像高斯噪声.

1.1 非局部均值滤波

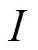
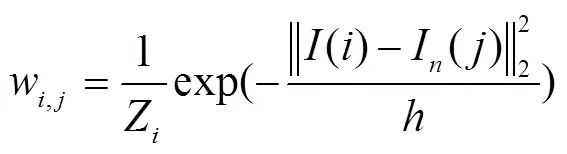
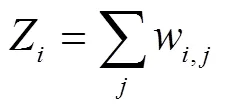
1.2 方法噪声

方法噪声一方面反映估计图像信息缺失情况，另一方面反映噪声分布情况，其被定义为噪声图像与估计图像之差：

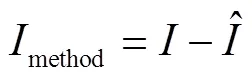
通常，方法噪声含有一定边缘信息，和和如图2所示.

2 本文方法

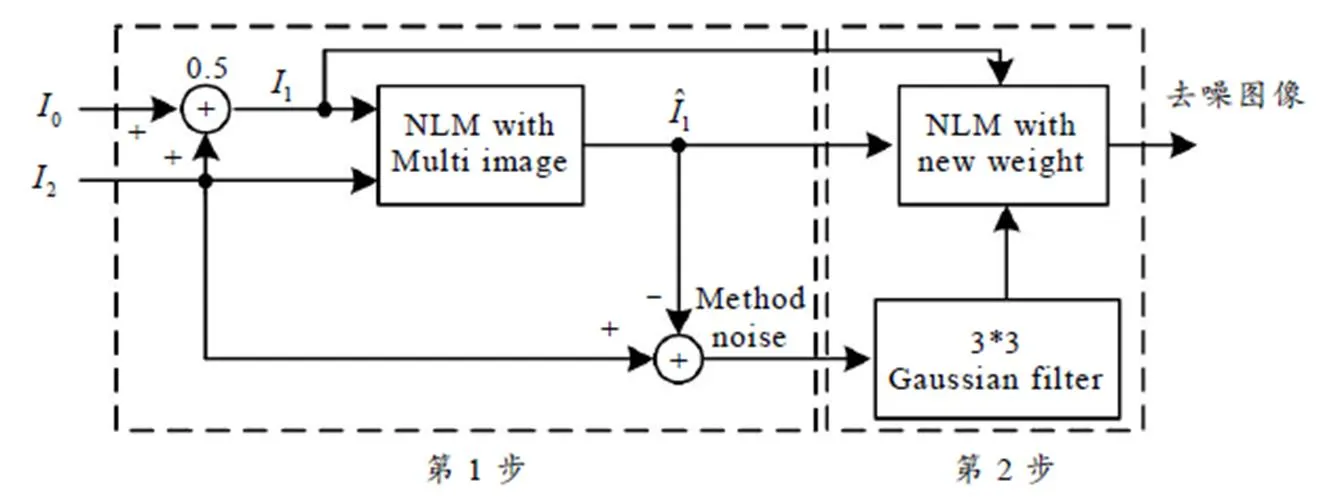
图3 本文方法示意图

2.1 多图像线性叠加非局部均值

2.2 高斯滤波与多图像非局部均值

假设清晰图像已知，利用清晰图像估计权值比噪声图像更可靠[10]，结合式（10）估计清晰图像中参考块与相似块欧氏距离平方得式（11）.

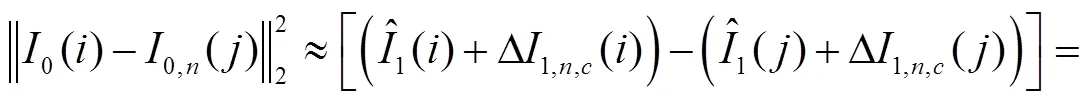
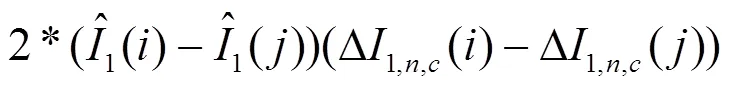
其中，估计使用经验式子[10]，即，为噪声方差，参考块和搜索窗口大小分别为5*5和11*11，参数和取实验经验值，分别为2.22和11.71. 线性拟合如图4所示.

3 实验结果及分析

本实验在2.5 GHz Intel CPU和4G内存的笔记本电脑上，利用matlab R2016a进行仿真，测试图像有4张，分别为Barbara、Lena、Boat和House，其中前3张图像大小为512*512，最后一张大小256*256. 仿真实验双噪声图像来自对两幅相同图像分别添加高斯噪声得到. 为了更好说明本文算法进行图像去噪的有效性，本文实验结果分别与BM3D、KSVD、NLM以及文献[10]进行比较，实验结果见表1.

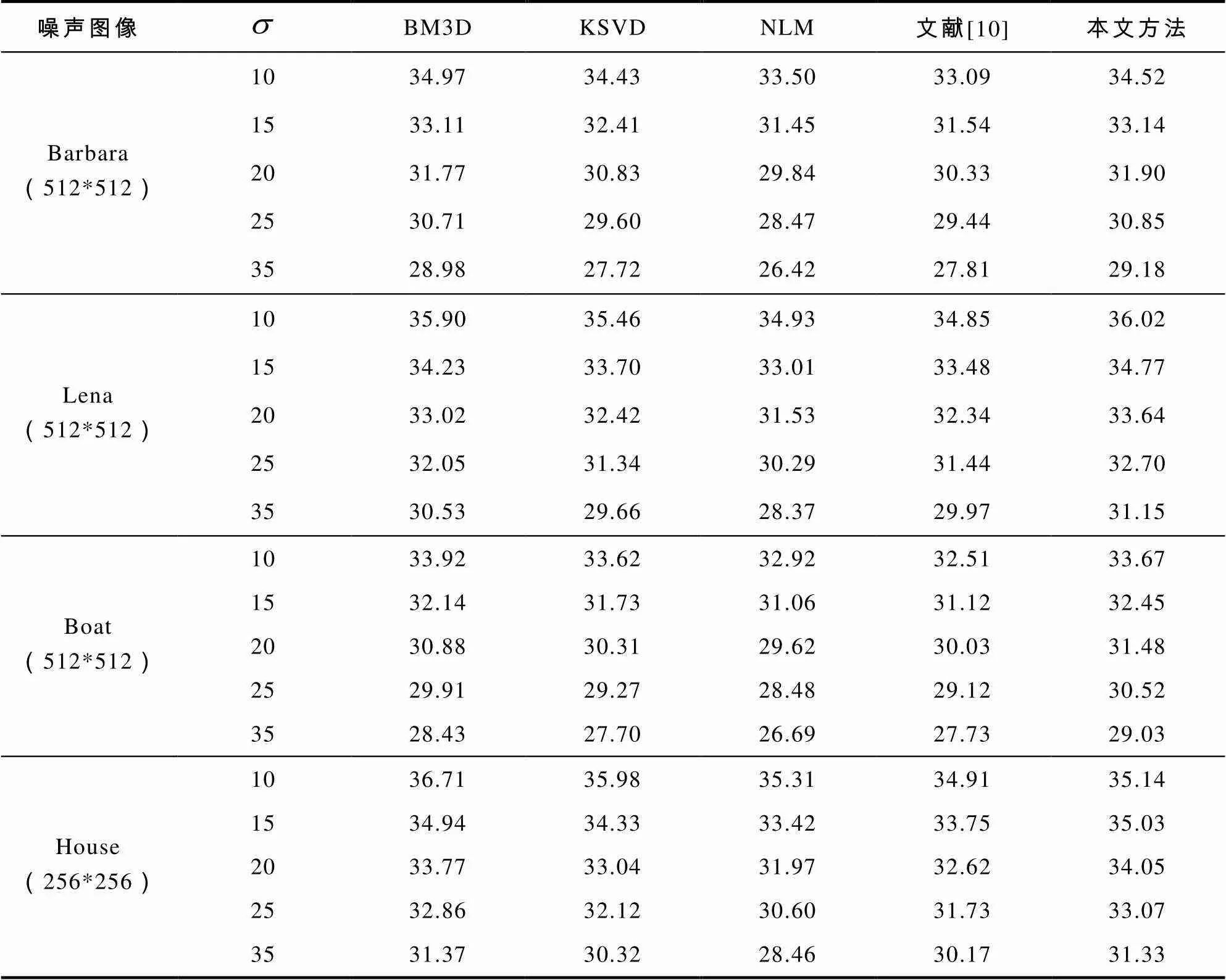
表1 不同方法去噪效果比较（PSNR）

图5 Lena和Boat图的PSNR变化

图7 Barbara、Lena原始图像和噪声图像

图8 采集图像分别用文献[10]与本文方法的去噪效果对比

图9 随机噪声与自然图像噪声分布

表2 拟合噪声分布方差

由图8-c、d实验结果与图9可知，本文方法对高斯噪声具有一定去噪效果，无论是在边缘还是平坦区域，相对于自然图像，噪声被滤波平滑去掉.

综上所述，相机在正常条件下采集图像的噪声为加性噪声，如式（1），这种噪声在空间域互不相关，通过线性叠加能够消除部分噪声. 非局部均值是利用相似图像块加权更新参考图像块，由于多幅图像能够提供关于相似块更多信息，优化了权值计算，故能够进一步去噪，获得预去噪图像. 最后对方法噪声采用高斯滤波能够更好抑制噪声，结合预去噪图像估计原始图像的权值，实现最终图像去噪.

4 结论

受多图像方法和文献[10]的启发，通过对比分析，设计了基于多图像非局部均值去噪方法，有两点改进：1）利用多幅噪声图像线性加权并结合多图像非局部均值滤波获得预去噪图像和方法噪声；2）考虑到方法噪声主要包含图像边缘信息，对方法噪声采用高斯滤波，联合预去噪图像求解像素权值，利用非局部均值滤波获得最终图像. 仿真实验表明，本文方法较其他方法能获得较好PSNR，对图像平坦区域具有良好去噪效果，对于纹理或边缘处也能去除一定噪声. 对于含有高斯分布噪声的自然图像，也具有一定去噪效果. 由于该方法目前只适用于静态图像去噪，如何应用到动态图像去噪是下一步研究方向.

[1] DIVAKAR N, BABU R V. Image denoising via CNNs: An adversarial approach [C]//New Trends in Image Restoration and Enhancement, Honolulu: CVPR workshop, 2017.

[2] BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising [C]//Computer Vision and Pattern Recognition, San Diego: IEEE CVPR, 2005: 60-65.

[3] DELEDALLE C A, DENIS L, TUPIN F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights [J]. IEEE Transactions on Image Processing, 2009, 18(12): 2661-2672.

[4] VILLE D V D, KOCHER M. SURE-based non-local means [J]. IEEE Signal Processing Letters, 2009, 16(11): 973-976.

[5] SALMON J. On two parameters for denoising with non-local means [J]. IEEE Signal Processing Letters, 2010, 17(3): 269-272.

[6] LEVIN A, NADLER B. Natural image denoising: optimality and inherent bounds [C]//Computer Vision and Pattern Recognition, Colorado: IEEE CVPR, 2011: 2833-2840.

[7] BUADES A, LOU Y, MOREL J M，et al. Multi image noise estimation and denoising [J]. Image Processing, 2010: 1-28.

[8] LIU Ce, FREEMAN W. A high-quality video denoising algorithm based on reliable motion estimation [J]. Computer Vision–ECCV, 2010, 6313: 706-719.

[9] ZHANG Li, VADDADI S, JIN Hailin, et al. Multiple view image denoising [C]//Computer Vision and Pattern Recognition, Miami: IEEE CVPR, 2009: 1542-1549.

[10] ZHONG Hua, CHEN Yang, ZHANG Xiaohua. A new weight for nonlocal means denoising using method noise [J]. IEEE Signal Processing Letters, 2012, 19(8): 535-538.

[11] WANG Xingzheng, WANG Haoqian, YANG Jiangfeng, et al. A new method for nonlocal means image denoising using multiple images [J]. PLoS One, 2016, 11(7): e0158664.

[责任编辑：韦 韬]

A Study of Non-local Means Image Denoising Based on Multiple Images

CHENYin-xing, SHANGLi-juan

(School of Information Engineering, Wuyi University, Jiangmen 529020, China)

In order to improve the effect of image denoising, this paper presents a method based on multi-image non-local means denoising. First, pre-denoised images and method noise are obtained by combining multiple noise image linear weighted sum and multi-image NLM. Then Gaussian filtering is performed on the method noise and then combined with the pre-denoised image and the input image, and the final denoised image is obtained by using a multi-image NLM. Experimental results of Gaussian noisy images show that, compared with the single image denoising method of NLM, the proposed method can improve the peak signal to noise ratio by 0~2 dB, effectively improving the visual effect.

multi-image denoising; method noise; non-local mean; Gaussian filtering

TP391.4

A

1006-7302（2018）02-0031-07

2018-03-12

陈银星（1990—），男，湖南衡阳人，在读硕士生，主要研究方向为数字图像处理.