主动围压下花岗岩动态力学特性与本构模型研究
2018-06-07李鸿儒王志亮郝士云
李鸿儒,王志亮,郝士云
(合肥工业大学土木与水利工程学院,安徽 合肥 230009)
随着社会对矿产资源的需求不断增长,深部资源的开发和利用成为国家资源能源安全的重大问题[1]。而深部地质力学环境复杂,岩体往往受到多个方向荷载的影响,在瓦斯爆炸和矿井冲击地压等工程灾害中均伴随着冲击荷载的作用。因此,开展动载下岩石三维力学特性的研究具有重要意义。
Xia等[2]探讨了微观结构对barre花岗岩动态压缩特性的影响,发现低应变率下动态压缩使试样预先存在的微裂纹扩展,而高应变率下试样则从两端开始破坏。三轴SHPB试验条件较为复杂,有关试验开展较晚,成果相对较少。王林等[3]探讨了大理岩和磁铁石英岩在围压和冲击荷载耦合下的破坏机理,得出岩石的破坏类型大致分为四种,其中以剪切和拉剪破坏为主;宫凤强等[4]利用三轴SHPB动静组合加载装置对砂岩进行了冲击试验,结果表明岩石动态抗压强度随着围压和应变率的提高而提高。
众所周知,本构方程反应材料的固有特性,一直是岩石力学研究的热点,产生了诸如Maxwell、Kelver与Bingham体等经典组合模型。损伤统计强度理论的发展也取得了许多成果,汪辉平等[5]定义了考虑损伤阈值的新型损伤模型,且能反映岩石的体积变化和初始孔隙率的影响。在组合模型中考虑损伤是发展岩石本构的一种新方式,如蔡灿等[6]提出了适用于中低应变率下岩石的本构模型并与试验进行了对比分析;翟越等[7]建立结合损伤的黏弹性本构模型,并利用反演分析法再生应力-应变曲线。然而,以上两个模型适用于应力-应变曲线加载段,无法对卸载段曲线进行很好的拟合。
本文利用改进的SHPB试验装置,对黑云母花岗岩开展了4种围压(0,2.5,5和10 MPa)下的动态冲击压缩试验,基于试验结果探究了此类岩石的应力-应变曲线形态、抗压强度和弹性模量等力学特性,同时构建了考虑损伤的组合元件本构模型,并与试验结果进行对比,分析了相关参数对模型精度的影响,以期为相关研究提供参考。
1 三轴动态压缩试验
1.1 试样取材与制备
花岗岩材料取自陕西华山地区,外观呈灰白色,块状构造,主要由斜长石、微斜长石和石英组成,含有黑云母成分,呈半自形-他行粒状结构,粒径在0.7~4 mm之间,具体矿物组成见表1。
为了满足实验要求消除惯性效应,将试样切割打磨为直径50 mm、厚度25 mm的圆柱体,并将试样两端面的平行度控制在±0.05 mm以内(图1)。该花岗岩静态单轴抗压强度为138 MPa,泊松比为0.24。

图1 花岗岩试样Fig.1 Granite specimens
1.2 测试设备及方法
试验采用改进的SHPB装置(图2),包括主体设备、发射系统和测试系统等部分,围压施加主要有两种方式:被动围压和主动围压。前者是利用试样外侧钢制套管限制试样变形从而对试样施加围压,后者是通过油压缸内的液体预先对试样四周施加可调控的预定围压[8]。被动围压虽操作简便,但只能通过改变套管材料和尺寸来改变围压,且试验中围压值不恒定,因此本文采用易于控制围压大小的主动围压装置,其由油缸、隔油橡胶套、液压油进出口、支座等构成。发射系统采用“纺锤形”冲头[9],冲击过程中产生的半正弦波不仅能防止脆性材料测试时的提前破坏,还能有效避免信号振荡,并保持试样的近似恒应变率变形;冲头和压杆材料均采用高强度合金,密度为7 810 kg/m3,弹性模量为210 GPa,入射、透射与吸收杆长度分别为2.4,1.2,1.0 m,直径均为50 mm。利用示波器和超动态应变仪记录入射和透射杆的应变片上所获得的入射、反射和透射电压信号,经由“三波法”[10]处理后获得应力、应变和应变率等试验数据。
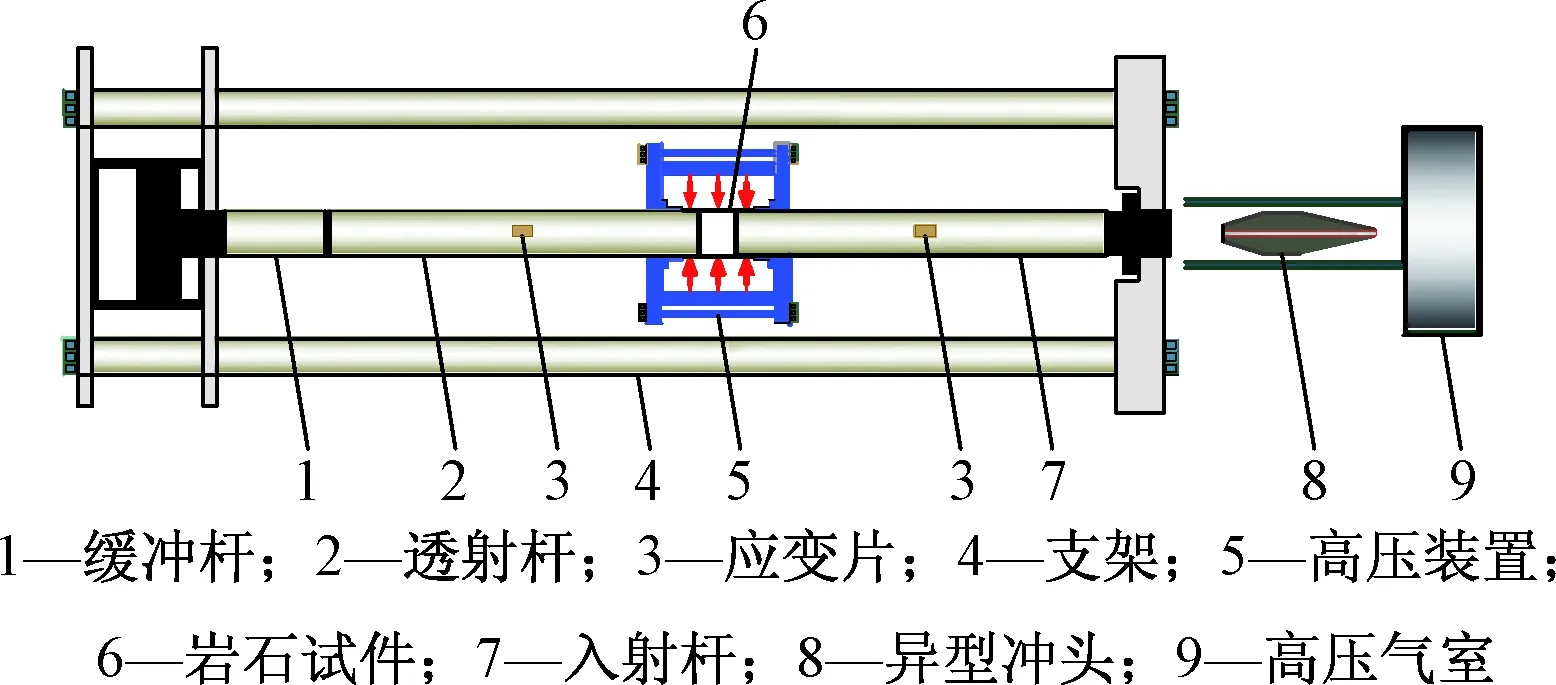
图2 SHPB装置示意图Fig.2 Schematic diagram of the SHPB equipment
试验共采用0,2.5,5,10 MPa共4种围压,每种围压下准备4~8个试样,确保每组有4个有效数据。通过调节气压大小或子弹的位置实现不同应变率加载。为减小端面摩擦,试验前在试样两端涂抹黄油,调整入射杆、透射杆和试样中心对齐,夹紧试样后预先施加围压到设定值并保持稳定,再进行冲击压缩试验。
2 三轴动态压缩试验结果分析
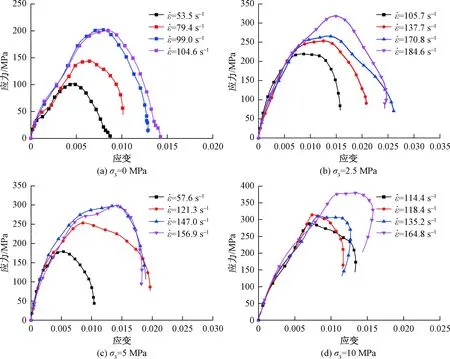
图3 不同围压下动态压缩应力-应变曲线Fig.3 Dynamic compressive stress-strain curves under different confining pressures
2.1 试验结果及应力-应变曲线
花岗岩三轴动态压缩试验结果如表2所示,可见在一定围压下,花岗岩试样的峰值应力与峰值应变均表现出明显的应变率正相关性。相应的应力-应变曲线如图3所示。单轴冲击压缩试验中应力-应变曲线的上升段大部分为弹性阶段,而屈服阶段较短,随着围压的增大,试样的塑性变形增加,曲线出现明显的塑性屈服平台,在高围压下(如10 MPa)应力-应变曲线卸载段出现回弹,此时岩样仍具备一定的承载能力,破坏程度有所降低。
2.2 动态强度增长因子与弹性模量
工程材料大多表现出应变率敏感特性,不少研究者[11]采用动态强度增长因子(DIF)衡量冲击荷载下材料抗压强度随应变率的变化幅度,即试样动态抗压强度与静态抗压强度的比值:
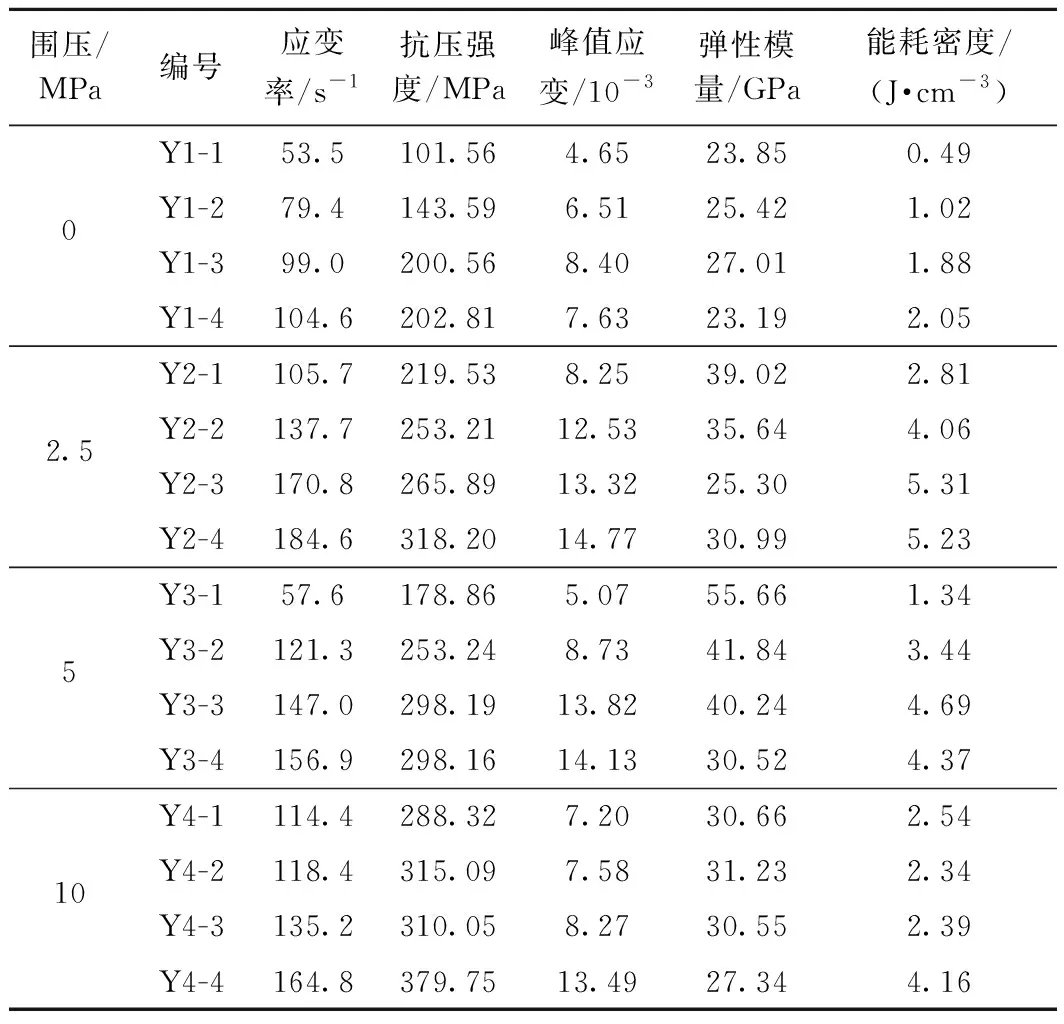
表2 不同围压下的试验结果Table 2 Testing results under different confining pressures
(1)
式中:fc,d,fc,s——试样的动态、静态抗压强度。
图4为不同围压下试样动态强度增长因子随应变率变化关系。可见当围压一定时,花岗岩动态强度增长因子随着应变率的增大而增大,体现出明显的应变率效应;围压对花岗岩抗压强度影响显著,围压的存在抑制了岩石内部裂纹的扩展,提高了花岗岩的抗冲击性能,10 MPa围压下试样抗压强度普遍为静态压缩的两倍以上。岩石应力-应变曲线往往可以分为多个阶段,曲线的上升段表现出一定的非线性,故而弹性模量的大小与所采取的计算方式有关。本文弹性模量采用曲线峰值强度40%和60%两点连线的斜率,弹性模量与应变率及围压的关系见图5。可见随着应变率的变化,花岗岩弹性模量的变化无明显规律;围压下花岗岩的弹性模量较单轴时有所上升,但总体上数据的离散性较大,可能是试样本身的离散性所致,弹性模量整体处于23~42 GPa范围内。
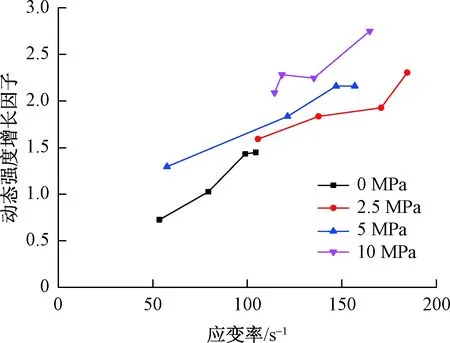
图4 不同围压下动态强度增长因子随应变率变化Fig.4 Variation of dynamic increase factor with strain rate
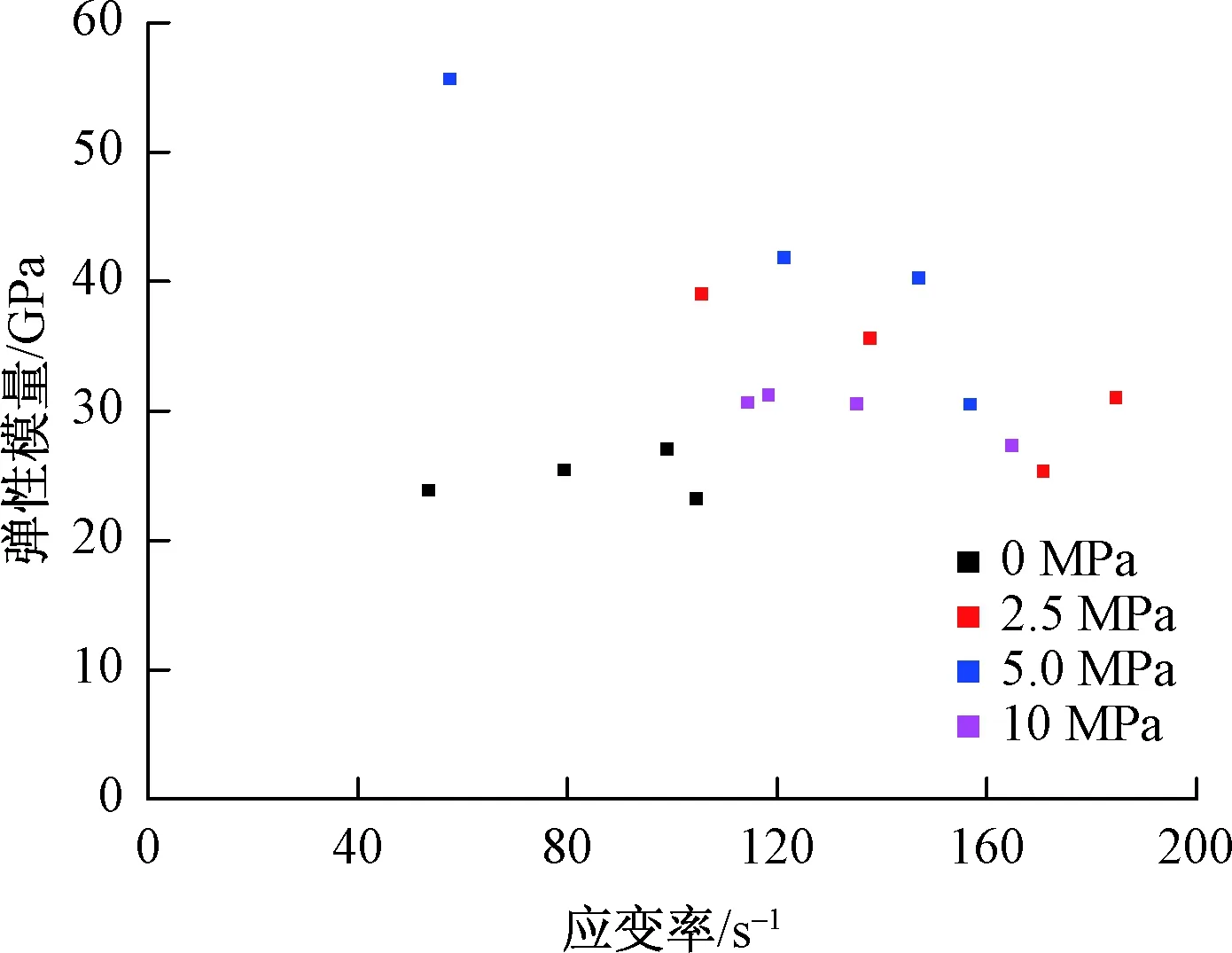
图5 不同围压下弹性模量随应变率变化Fig.5 Variation of elastic modulus with strain rate
3 花岗岩本构模型的建立
岩石力学中常见的本构模型有多种,在黏弹性连续介质力学中,将弹性、黏性等介质不同组合能够满足描述工程中所遇到的各类岩石本构方程的需要。其中,鲍埃丁模型的效果较好,它由一个弹性体与一个黏滞体串联成Maxwell体,再与一个弹性体并联而成。
材料内部存在的微裂纹、微孔洞等各类缺陷在外载和环境作用下不断劣化导致体积单元破坏从而产生损伤。损伤几乎伴随着应力-应变曲线演化的全过程,故而在岩石的动态本构关系中考虑损伤的影响很有必要。此处采用损伤体代替鲍埃丁模型中并联的弹性体,所得的岩石损伤模型如图6所示。
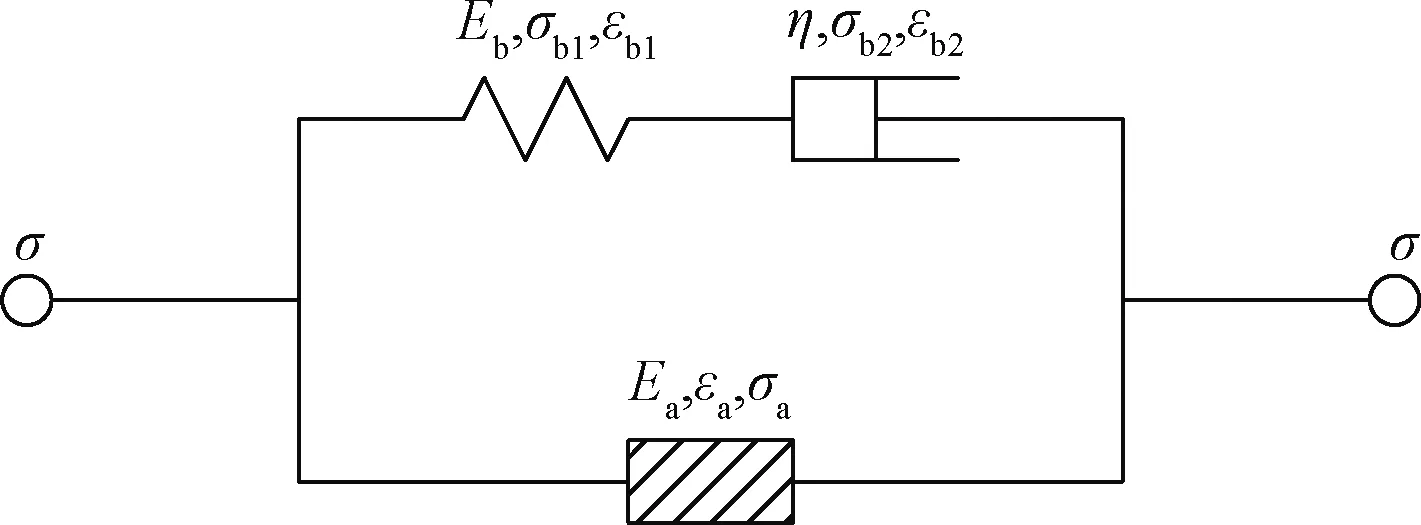
图6 岩石损伤模型Fig.6 Damage model of rock
图6中符号Ea,σa,εa和Eb,σb1,εb1分别为损伤体和弹性体的弹性模量、应力和应变;σb,εb和σb2,εb2分别为Maxwell体和黏滞体的应力及应变;η为黏滞体的黏性系数;σ和ε为模型整体的应力和应变。
假设岩石由无数个“微元”组成,其力学性质宏观表现为各向同性,根据Lemaitre应变等价性假设[12],损伤材料的本构关系与无损状态下的本构关系形式相同,只是将其中的真实应力替换成有效应力。试验中试样四周围压处处相等,可得岩石材料的损伤本构关系为:
(2)
式中:σ1,σ2,σ3——名义第一、第二和第三主应力;
σ1*,σ3*——有效第一和第三主应力;
D——岩石损伤变量。
假设岩石微元体在破坏前具有线弹性性质,根据广义胡克定律可知:
(3)
由式(2)和(3)可得:
σ1=Eε1(1-D)+2μσ3
(4)
引入统计学的方法,假设岩石微元强度F*服从Weibull随机分布,根据应变强度理论,F*可以用ε代替[13],其概率分布函数为:
(5)
式中:m,α——Weibull分布参数。
岩石变形破坏时材料内部的损伤是一个不断累积的连续过程,对式(5)积分可得损伤D:
(6)
由式(4)和(6)可知:
(7)
模型中Maxwell体与损伤体并联,因而:
σ(t)=σa(t)+σb(t)
(8)
ε(t)=εa(t)=εb(t)
(9)
在Maxwell体中,弹性体与黏滞体串联:
σb(t)=σb1(t)=σb2(t)
(10)
εb(t) =εb 1(t)+εb 2(t)
(11)
对式(10)和(11)两边同时求微分:
(12)
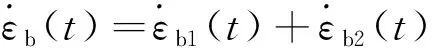
(13)
弹性体与黏滞体方程分别为:
σb 1(t) =Ebεb1(t)
(14)
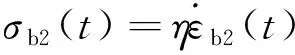
(15)
对式(14)两边求微分可得:
(16)
把式(12)、(15)和(16)代入式(13):
(17)
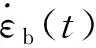
(18)
式中:S——复变量。
对式(18)两边进行Laplace逆变换:
(19)
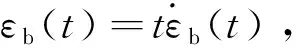
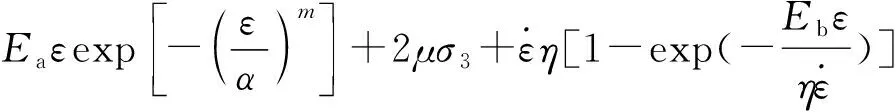
4 本构模型的参数分析与试验验证
4.1 参数分析
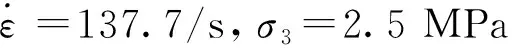
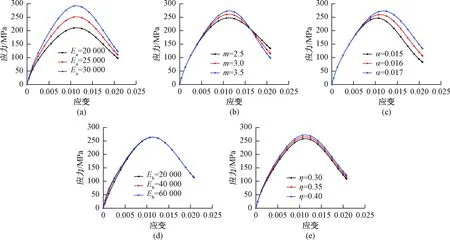
图7 各参数对拟合曲线的影响Fig.7 Influence of each parameter on the fitting curve
4.2 试验验证
为了验证本文所提出的花岗岩本构模型的合理性,选取试验所得的4种围压和3种应变率下的数据代入式(20)中进行拟合(图8,表3)。围压和应变率对岩石的泊松比影响较小[14],故而拟合时泊松比取定值μ=0.24。
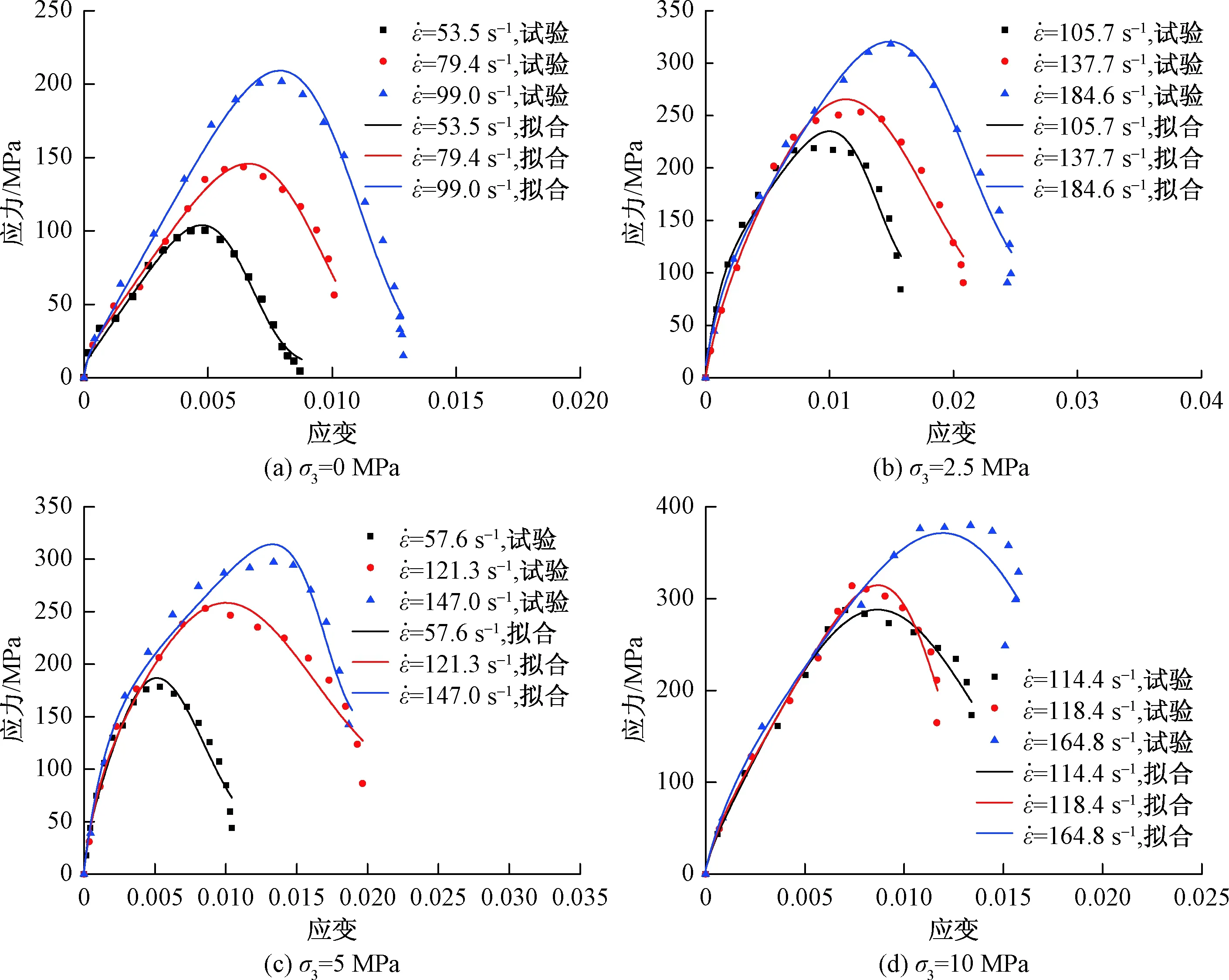
图8 试验与理论曲线比较Fig.8 Comparison of theoretical curves with measured curves
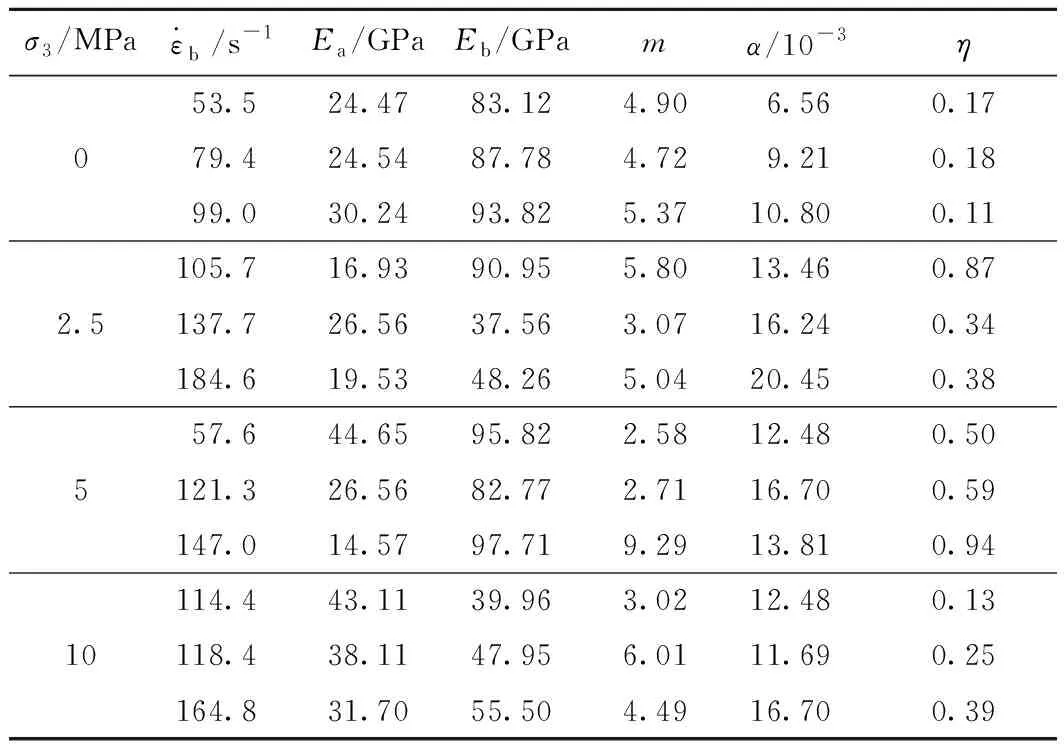
表3 花岗岩本构模型参数拟合结果Table 3 Fitting results of granite constitutive parameters
由图8可知,本文所建立的本构模型与试验加卸载段吻合均较好,适用于花岗岩全应力-应变曲线的拟合,10 MPa下曲线的拟合优度有所下降,这是因为高围压下试样应力-应变曲线的卸载段有一定回弹。由表3可见,参数α的值在峰值应力对应的峰值应变附近变化,且随着应变率和围压的增大而增大;m基本处于3~6之间;黏性系数η集中分布在0.1~0.5之间,围压下花岗岩的黏性系数有所增大。
5 结论
(1)随着围压的增大,花岗岩的塑性增强,应力-应变曲线出现塑性屈服平台,高围压下曲线有一定回弹现象。应变率与围压的增大提高了岩样的承载能力,两者与动态强度增长因子均为正相关。应变率和围压对弹性模量影响不明显。
(2)Weibull分布中的参数m与α对屈服阶段以后的应力-应变曲线有明显影响,其中α随着应变率和围压的增大而增大;随着Ea的增大,曲线加载和卸载段斜率上升;Eb仅对屈服强度以前的曲线有一定影响;η的影响伴随着应力-应变曲线的全过程。
(3)在鲍埃丁模型中引入统计损伤理论,将Maxwell体与损伤体并联,所得的本构模型参数较少,易于确定,能应用于花岗岩全应力-应变曲线的表征,经对比与试验所得的应力-应变曲线有较高的吻合度。
参考文献:
[1] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J]. 岩石力学与工程学报,2005,24(16):2803-2813.[HE M C, XIE H P, PENG S P,etal. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803-2813.(in Chinese)]
[2] Xia K, Nasseri M H B, Mohanty B,etal. Effects of Microstructures on Dynamic Compression of Barre Granite[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(6):879-887.
[3] 王林,于亚伦.三轴SHPB冲击作用下岩石破坏机理的研究[J]. 爆炸与冲击, 1993(1):84-89.[WANG L, YU Y L. The dynamic fracture mechanism of rocks under SHPB confining pressure[J]. Explosion and Shock Waves,1993(1):84-89.(in Chinese)]
[4] 宫凤强,李夕兵,刘希灵.三轴SHPB加载下砂岩力学特性及破坏模式试验研究[J].振动与冲击,2012, 31(8):29-32.[GONG F Q, LI X B, LIU X L. Tests for sandstone mechanical properties and failure model under triaxial SHPB loading[J]. Journal of Vibration and Shock, 2012, 31(8):29-32.(in Chinese)]
[5] 汪辉平,曹文贵,王江营,等.模拟岩石应变软化变形全过程的统计损伤本构模型研究[J].水文地质工程地质, 2013, 40(4):44-49.[WANG H P, CAO W G, WANG J Y,etal. A study of the statistical damage constitutive model of rocks considering a full deformation process[J]. Hydrogeology & Engineering Geology, 2013, 40(4):44-49.(in Chinese)]
[6] 蔡灿,伍开松,袁晓红,等.中低应变率下的岩石损伤本构模型研究[J].岩土力学,2015,36(3):795-802.[CAI C, WU K S, YUAN X H,etal. Damage constitutive model of rock under medium and low strain rates[J]. Rock and Soil Mechanics, 2015, 36(3): 795-802.(in Chinese)]
[7] 翟越,赵均海,李寻昌,等.岩石类材料损伤黏弹塑性动态本构模型研究[J].岩石力学与工程学报,2011,30(增刊2):3820-3824.[ZHAI Y, ZHAO J H, LI X C,etal. Study of damage viscoelasto-plastic dynamic constitutive model of rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2011,30(Sup 2):3820-3824. (in Chinese)]
[8] 吴赛,赵均海,李楠,等.被动围压下混凝土的动态力学性能研究[J].应用力学学报,2015,32(6):992-999.[WU S, ZHAO J H, LI N,etal. Numerical simulation on a connection of prestressed concrete-steel hybrid wind turbine tower[J]. Chinese Journal of Applied Mechanics, 2015,32(6):992-999. (in Chinese)]
[9] Li X B, Lok T S, Zhao J. Dynamic characteristics of granite subjected to intermediate loading rate[J]. Rock Mechanics & Rock Engineering, 2005, 38(1):21-39.
[10] 宋力,胡时胜.SHPB数据处理中的二波法与三波法[J]. 爆炸与冲击,2005,25(4):368-373.[SONG L, HU S S. Two-wave and three-wave method in SHPB data processing[J].Explosion and Shock Waves, 2005, 25(4):368-373.(in Chinese)]
[11] 刘石,许金余,刘军忠,等.绢云母石英片岩和砂岩的SHPB试验研究[J].岩石力学与工程学报,2011, 30(9):1864-1871.[LIU S, XU J Y, LIU J Z,etal. SHPB experimental study of sericite-quartz schist and sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9):1864-1871.(in Chinese)]
[12] Lemaitre J. How to use damage mechanics[J]. Nuclear Engineering and Design, 1984, 80(2): 233-245.
[13] Li Y, Jia D, Rui Z,etal. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage[J]. Journal of Petroleum Science & Engineering, 2017, 153:123-132.
[14] 陈勇,王志亮.华山花岗岩动力学行为与破坏准则研究[J].水文地质工程地质,2014,41(3):66-69.[CHEN Y, WANG Z L. A Study of the dynamic behavior and failure criterion of the granite in Huashan[J]. Hydrogeology & Engineering Geology,2014,41(3):66-69.(in Chinese)]
