区分快慢变子系统的柔性机械臂组合控制*

方 俊

(北京京北职业技术学院，北京 101400)

0 引言

机械臂可以代替人类完成劳动强度大、安全风险高、操作复杂的工作，传统的刚性机械臂基座粗壮、臂杆短，存在灵活性差、能耗大、定位精度低、反应速度慢等问题[1]，不适应航天、医疗等领域。灵活性好、能耗低、响应快的柔性机械臂在航空航天、高精密制造中越来越受到重视，但是柔性机械臂在使用中会发生形变和振动，对系统稳定性和操作精确性影响很大[2]。因此研究柔性机械臂控制方法，对提高系统稳定性和操作精确性具有现实意义。

机械臂的控制方法可以分为以下几种：①基本控制方法，也就是基于模型的控制方法[3]；②自适应控制，在线估计未知参数并调整控制策略[4]；③PID控制[5]；④变结构控制[6]；⑤鲁棒控制[7]；⑥模糊控制；⑦迭代学习控制[8]；⑧神经网络控制；⑨最优控制；⑩奇异摄动控制[9]等。这些方法各有优缺点，比如PID控制简单、无需建模，但是稳定性较差；模糊控制优点是不需要系统模型，缺点是控制精度低等。

本文目的是提高柔性机械臂控制精度，使用拉格朗方程建立了动力学方程，使用奇异摄动法将系统分解为快变和慢变子系统，分别设计了快慢变子系统控制器。通过仿真结果看出，自适应滑膜变组合控制器具有跟踪速度快、跟踪过程无震荡、控制器输出平稳等优势。

1 柔性机械臂建模

本文研究对象为双连杆柔性机械臂。柔性机械臂包括关节柔性和臂杆柔性两个方面，其中关节柔性非常复杂，本文忽略关节柔性，只研究臂杆柔性，臂杆柔性包括弹性形变、剪切形变和轴向形变三个方面，而柔性机械臂的臂长远远大于截面直径，因此剪切形变和轴向形变相对于弹性形变可以忽略不计，基于以上分析，本文将柔性机械臂简化为Euler-Bernoulli梁。

1.1 拉格朗日方程

本文使用拉格朗日方程和假设模态法建立柔性机械臂动力学方程。

拉格朗日方程描述为：

(1)

式中，L为拉格朗日函数，Q为广义力，z为广义坐标变量。拉格朗日函数L=T-V-U，式中T为系统总动能，V为总势能，U为总应变能。

1.2 柔性机械臂力学分析

建立柔性机械臂的割线坐标系如图1所示。图中OXY为惯性坐标系，OiXiYi为连杆Li的割线坐标系，qi为第i个连杆的转角，mi为连杆i的末端集中质量，wi(xi,t)为t时刻、连杆i在xi处的横向形变。记连杆i的长度为Li、质量为Mi。

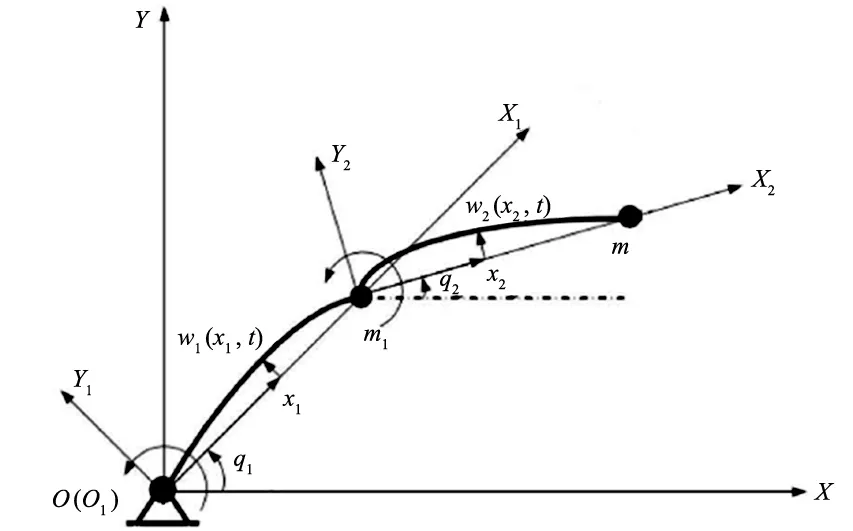
图1 双连杆柔性机械臂割线坐标系

根据假设模态法[10]和振动分析理论，wi(xi,t)为：

(2)

其中，pij(t)为弹性模态坐标矢量，j为模态标号，n为模态数。

连杆1任意一点坐标可表示为：

r1=[x1cosq1-w1sinq1,x1sinq1+w1cosq1]T

(3)

对上式求导，得到连杆1上任意一点速度为：

(4)

将x1=L1代入到上式，可以得到连杆1末端位置速度为：

经过以上分析，连杆1的动能为：

同理可以推导出连杆2的动能T2，则柔性机械臂系统总动能T为：

(5)

柔性机械臂系统总势能V为重力势能，即

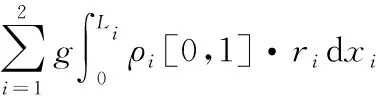
(6)

其中，ρi为连杆的线密度。

柔性机械臂产生的弹性形变还会产生应变能为：

(7)

其中，Ei为连杆i的弹性模量，Ii为连杆i的惯性矩。以上公式中点是对时间的倒数，撇是对xi的倒数。

1.3 建立动力学方程

拉格朗日方程在柔性机械臂系统中具体形式为：

(8)

其中,i=1,2，j=1,2,…,n。将式(5)～式(7)代入到拉格朗日方程中，结合正交原理，得到柔性机械臂系统的动力学方程为：

(9)

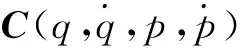
2 组合控制器设计

首先使用奇异摄动分解法将机械臂动力学方程分为快变子系统和慢变子系统。记N为M的逆矩阵，即：

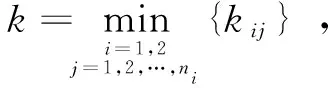
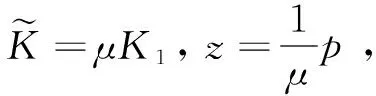
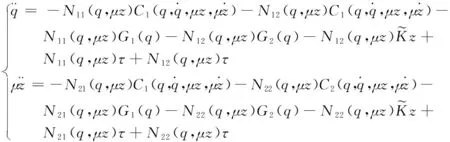
由于小参数μ的存在，上式在快变量中显示边界层现象，令μ=0可以得到慢变子系统动力方程为：

(10)

其中，上标s表示此变量为慢变量，慢变子系统描述柔性臂的刚性运动。

(11)

其中上标f表示此变量为快变量，快变量子系统描述柔性机械臂的弹性振动。

基于式(10)和式(11)，组合控制器设计原理如图2所示。

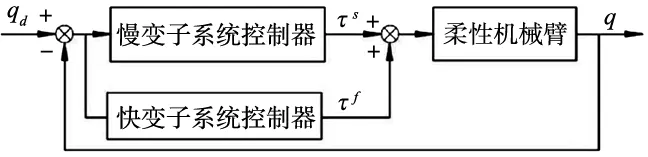
图2 组合控制器原理

图中qd为柔性机械臂期望输出，q为实际输出，τs、τf分别为慢变量和快变量控制力矩。

3 快慢变子系统设计

3.1 慢变子系统控制器

本文使用滑膜变结构控制慢变子系统，但是当系统存在较大不确定性和较大干扰时，系统会产生较大的抖振，甚至影响系统稳定性，因此本文提出了自适应滑膜变结构控制，就是使用自适应算法估计系统未知参数，再根据估计值和滑膜运动条件设计控制器，具体如图3所示。

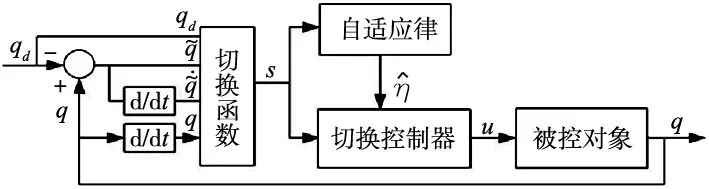
图3 自适应滑膜变结构控制器

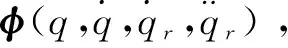
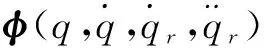
滑膜变结构控制率设计为：

(12)

(13)

式中要求Γi>0。

为了分析上述控制系统的稳定性，构造Lyapunov函数为：

(14)

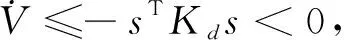
3.2 快变量子系统控制器

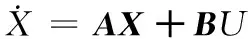
(15)

控制目标是振动最小、控制使用能量最小，因此将性能函数设置为：

(16)

其中，R、Q为对称正定矩阵，XTQX为动态振动能量，UTRU为能量消耗。

由状态方程可知快变量子系统为线性系统，由式(16)可知性能函数为状态变量和控制变量的二次型，因此快变子系统最优控制问题为线性二次型问题。根据极值原理，求解此线性二次型问题，得快变子系统最优控制为：

U=-R-1BTPX

(17)

其中，P为常数矩阵，为PA+ATP-PBR-1BTP+Q=0的解。

3.3 组合控制率

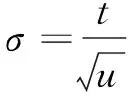
(18)

由式(12)和式(18)可以得到柔性机械臂的混合控制率为τ=τs+τf。

4 仿真验证及分析

为了验证组合控制器的优越性，同时使用传统的滑膜变结构和自适应滑膜变结构控制器对慢变子系统进行控制，采集10s的输出信号，结果分别如图4和图5所示。

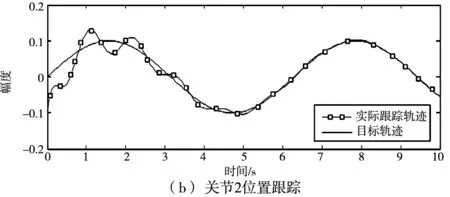
图4 传统滑膜变结构组合控制效果

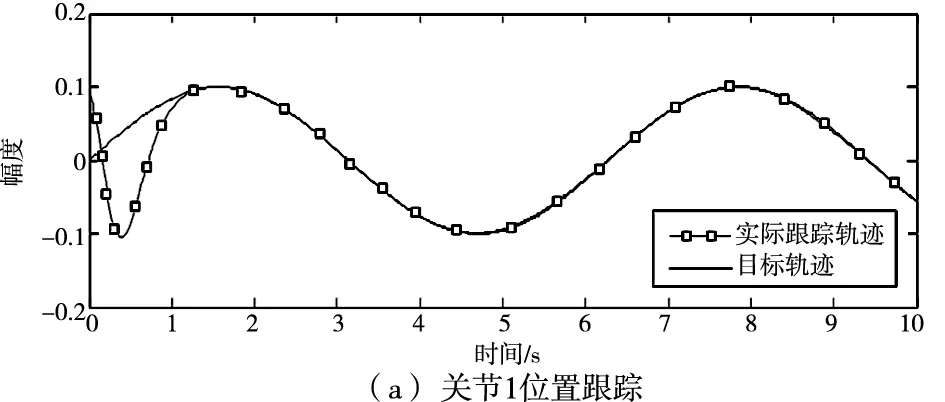
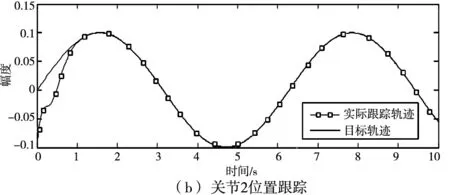
图5 自适应滑膜变结构组合控制效果

图4为传统滑膜变结构组合控制器对关节的位置跟踪效果，从图4a可以看出，从第6s时关节1大致跟踪目标轨迹，第8s时精确跟踪，从图4b可以看出，关节2从第5s时较精确跟踪目标轨迹。图5为自适应滑膜变结构组合控制器对关节位置的跟踪效果，从图5a可以看出，在1.5s时关节1精确跟踪目标曲线，从图5b可以看出，在1.3s时关节2精确跟踪目标曲线。所以自适应滑膜变结构组合控制器在调节时间上具有明显优势，除此之外，图4所示的控制过程存在长时间震荡过程，而图5所示的控制过程不存在震荡过程，也说明了自适应滑膜变组合控制器在关节位置跟踪上的优势。

为了进一步对自适应滑膜变组合控制器的优势进行挖掘，图6给出了关节1和关节2的期望控制输入曲线，图7给出了传统滑膜变结构组合控制器输入曲线与自适应组合控制器输入曲线。

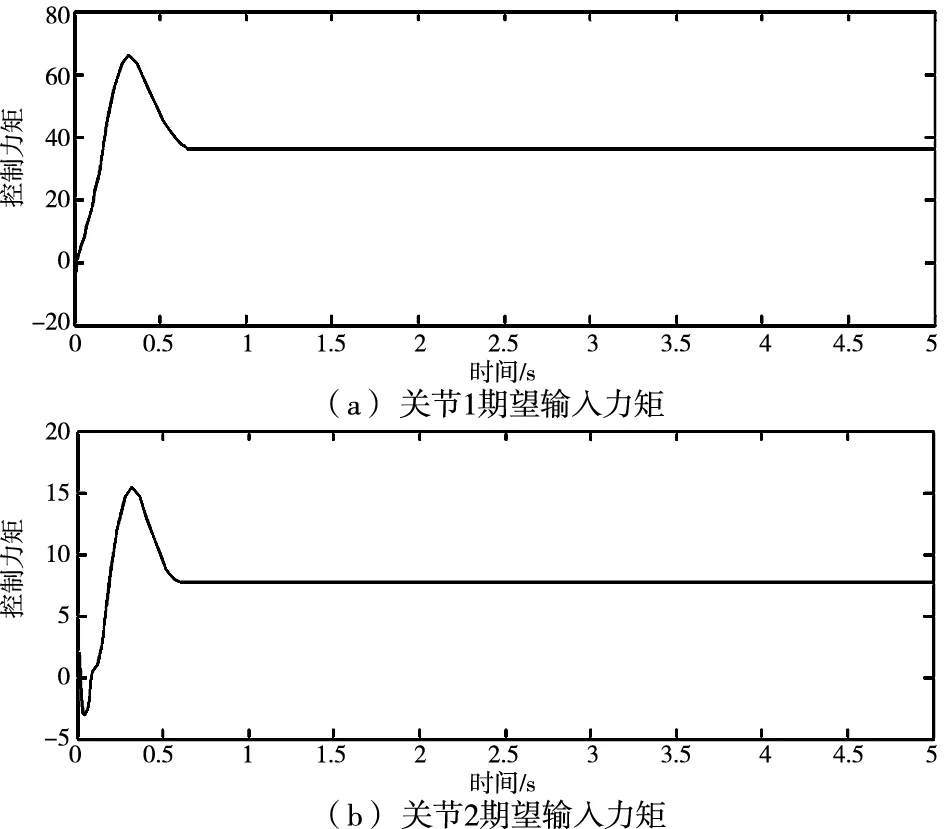
图6 各关节期望输入力矩

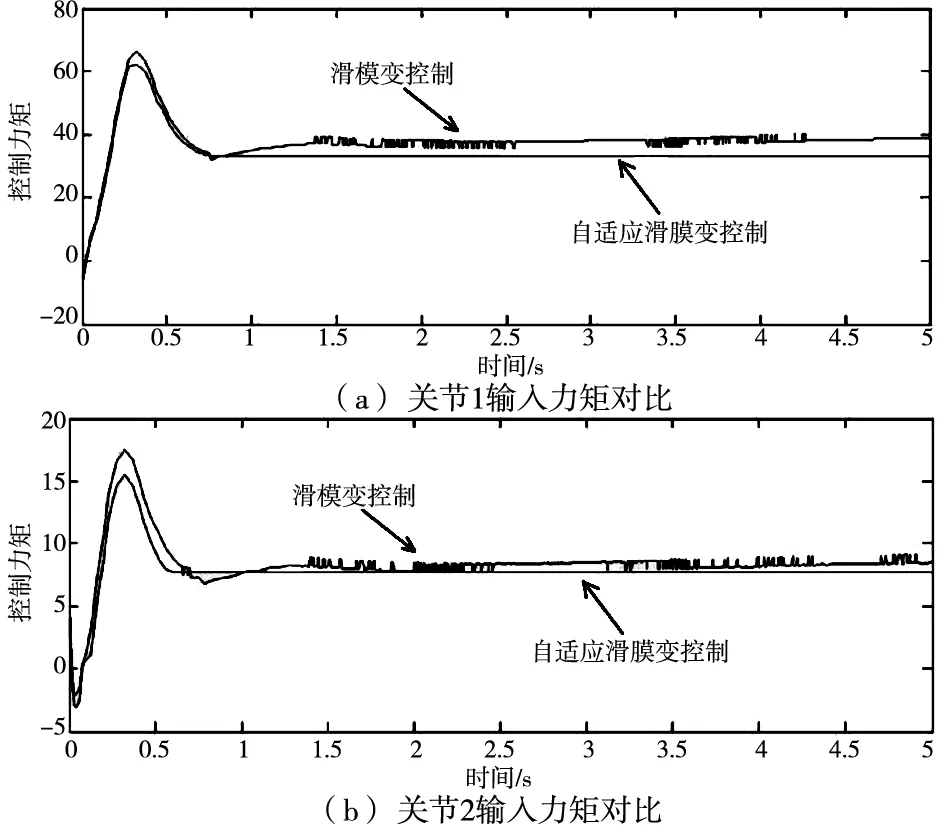
图7 各关节输入力矩

可以看出，滑膜变结构和自适应滑膜变结构组合控制器的输出力矩与期望输出力矩都很接近，但是滑膜变结构组合控制器输出存在明显的抖振现象，而自适应滑膜变结构组合控制器输出力矩平滑性很好，系统稳定性更强，控制效果更好。这是因为自适应滑膜变结构以误差和误差变化率为依据，对控制率进行了自适应调整，使得自适应滑膜变控制器的控制量平滑性好。

5 结论

本文建立了柔性机械臂的动力学方程，使用奇异摄动分解法将系统区分为快变子系统和慢变子系统，分别设计了快慢变子系统控制器，对传统滑膜变结构控制进行改进，提出了自适应滑膜变结构控制器，通过仿真可以看出：①相比于传统滑膜变结构控制，自适应滑膜变组合控制器跟踪目标轨迹更快、且跟踪不存在震荡过程，说明区分柔性机械臂的快慢变子系统，并分别设计控制器，对于柔性机械臂的控制非常有效；②自适应滑膜变组合控制器输出力矩平稳，不存在抖振现象，这是因为自适应滑膜变结构以误差和误差变化率为控制依据，自适应修改控制率，使控制器的输出控制量非常平滑。

[参考文献]

[1] 谷勇霞, 张玉玲, 赵杰亮,等. 柔性机械臂动力学建模理论与实验研究进展[J]. 中国机械工程, 2016, 27(12):1694-1703.

[2] 娄军强, 魏燕定, 杨依领,等. 智能柔性机械臂的建模和振动主动控制研究[J]. 机器人, 2014,36(5):552-559.

[3] 徐智浩, 李胜, 张瑞雷,等. 基于LuGre摩擦模型的机械臂模糊神经网络控制[J]. 控制与决策, 2014, 29(6):1097-1102.

[4] 陈明金, 李树荣, 曹乾磊. 时滞柔性关节机械臂自适应位置/力控制[J]. 控制理论与应用, 2015, 32(2):217-223.

[5] 曹青松, 周继惠, 黎林,等. 基于模糊自整定PID算法的压电柔性机械臂振动控制研究[J]. 振动与冲击, 2010, 29(12):181-186.

[6] 高新. 基于神经网络变结构控制的机械臂系统研究[D].哈尔滨:哈尔滨理工大学, 2012.

[7] Kalthoff D C, Mörs T, Tesakov A. Late Pleistocene small mammals from the Wannenköpfe volcanoes (Neuwied Basin, western Germany) with remarks on the stratigraphic range of Arvicola terrestris[J]. Geobios, 2007, 40(5):609-623.

[8] 孙继鹏, 孟德元, 杜明骏,等. 多机械臂的分布式自适应迭代学习控制[J]. 北京航空航天大学学报, 2015, 41(12):2384-2390.

[9] 于潇雁, 陈力. 参数不确定与有界干扰自由飘浮柔性空间机械臂基于速度观测器的奇异摄动鲁棒控制及振动抑制[J]. 振动与冲击, 2015, 34(14):85-92.

[10] 张春建, 王禹林, 韩军,等. 基于广义多项式假设模态法的大型螺纹旋风铣削工件系统动力学分析[J]. 组合机床与自动化加工技术, 2011(11):25-28.

[11] 万磊, 崔士鹏, 张国成,等. 欠驱动水下机器人航迹跟踪控制[J]. 电机与控制学报, 2013, 17(2):103-111.