直角坐标机器人迭代滑模交叉耦合控制器设计*

许鸣吉，李 胜，陈庆伟，郭 健，吴益飞

(南京理工大学 自动化学院，南京 210094)

0 引言

工业机器人是集机械、电子、控制、计算机、传感器、人工智能等多学科先进技术于一体的自动化装备，代表着未来智能装备的发展方向[1]。目前，国内外汽车、电子电器、工程机械等行业已大量使用工业机器人自动化生产线，以保证产品质量和生产高效率。

工业机器人按坐标形式可以划分为直角坐标型机器人、圆柱坐标型机器人、极坐标型机器人和多关节型机器人。作为工业机器人其中的一种类型，直角坐标机器人(Cartesian Robot)具有超大行程、负载能力强、动态特性高、扩展能力强、简单经济、寿命长等特性，由于可以在末端加持不同操作用途的工具，适用于多品种、便批量的柔性化作业，完成如焊接、码垛、包装、点胶、检测、打印等一系列作业。

直角坐标机器人的三轴运动控制是机器人的灵魂所在，对轮廓误差控制的好坏将直接影响末端执行器的位姿精度。目前，国内外学者对直角坐标机器人运动控制的研究着重于对单轴进行跟踪控制，主要手段包括摩擦力补偿、前馈控制和扰动补偿等。但是，上述方法对三轴同步、轨迹跟踪和轮廓误差控制的提升是有限的。系统外部扰动和参数摄动会严重影响三轴同步、轨迹跟踪和轮廓误差控制的精度[2]。

本文研究的主要问题是在不确定干扰下直角坐标机器人的高精度同步控制。首先，建立了三轴机器人直流电机模型和轮廓误差模型，与以往轮廓误差模型相比，本文所设计的模型结构简单，计算量小；然后，设计了滑模速度控制器，用以抑制非周期干扰，设计了迭代学习位置控制器，有效减小了周期性干扰和单轴跟踪误差，设计了轴间变增益交叉耦合控制器，用以消除系统的轮廓误差。分别对上述控制器逐一仿真验证，结果表明，所设计的迭代滑模交叉耦合控制器具有较高的轮廓精度和较强的鲁棒性。

1 直角坐标机器人轮廓误差模型

位置跟踪误差是指当前时刻的实际位置与期望位置的距离；而轮廓误差是指实际轮廓与期望轮廓之间的几何偏差，是比跟踪误差更为重要的性能指标[4]。精确的轮廓误差模型有利于提高直角坐标机器人末端执行器的位姿精度。图1为任意轨迹的实时轮廓误差模型。

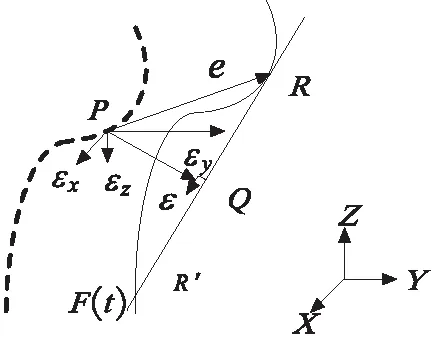
图1 任意轨迹的实时轮廓误差模型

如图1所示，假设t0时刻，在直角坐标系中，P为末端执行器的实际位置，坐标为(a,b,c)，F(t)为期望轨迹，R为期望位置，坐标为(x1,y1,z1),则PR为直角坐标机器人的跟踪误差向量，记作e，其在三轴上的投影分别为ex、ey、ez，即三轴各自的跟踪误差；R′坐标为(x0,y0,z0),直线RR′为轨迹F(t)在R处的切线；从P处向直线RR′作垂线，垂足为Q，坐标为(x,y,z)，则PQ为机器人的轮廓误差向量，记作ε，其在三轴上的投影分别为εx、εy、εz，即三轴各自的轮廓误差[5]。

由几何分析可得跟踪误差向量e和向量RR′的表达式为：

(1)

(2)

由R、Q、R′三点可求得直线RR′的线性方程为：

(3)

可求得向量PQ的表达式为：

(4)

已知直线PQ与直线RR′互相垂直，则向量PQ与向量RR′內积为零，表示为:

PQ·RR′=0

(5)

将式(2)和式(4)代入式(5)中，可求得:

(6)

将式(6)求出的参数t0代回式(3)，可得坐标点Q:

(7)

则轮廓误差向量ε的表示式为：

(8)

2 直流电机动态结构建模

直流电机具有良好的起动和制动性能，宜于在大范围内平滑调速，被广泛应用于许多调速和快速正反向的电力拖动领域[6]。本文以直流电机作为被控对象，需要建立直流电机的动态数学模型，再由其得到动态结构图。直流电机的电枢回路方程为：

(9)

式中，Ua为电枢电压，Id为电枢电流，E为感应电动势。忽略粘性摩擦和弹性转矩，可得到电机轴上的运动方程为：

(10)

式中，Te为电磁转矩，TL为负载转矩，J为转子转动惯量，ω为电机转速，GD2为电力拖动系统折算到电机轴上的飞轮矩。额定励磁下的感应电动势方程和电磁转矩方程分别为：

E=Cen

(11)

Te=CmId

(12)

式中，Ce为电动势常数，Cm为转矩系数。将式(11)和式(12)代入式(9)和(10)中并整理得：

(13)

(14)

式中，Tl=L/R，为电枢回路电磁时间常数，IdL=TL/Cm，为负载电流，Tm=GD2R/(375CeCm)，为机电时间常数。在零初始条件下，对式(14)取Laplace变换，得到电压与电流之间的传递函数：

(15)

对式(15)取Laplace变换，得到电流与电动势之间的传递函数：

(16)

由此得到直流电机动态结构框图，如图2所示。

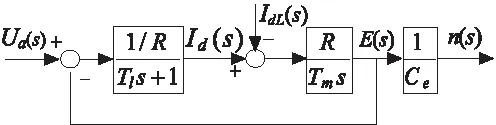
图2 直流电机动态结构图

3 迭代滑模交叉耦合控制器设计

如图3所示为迭代滑模交叉耦合控制器的结构。

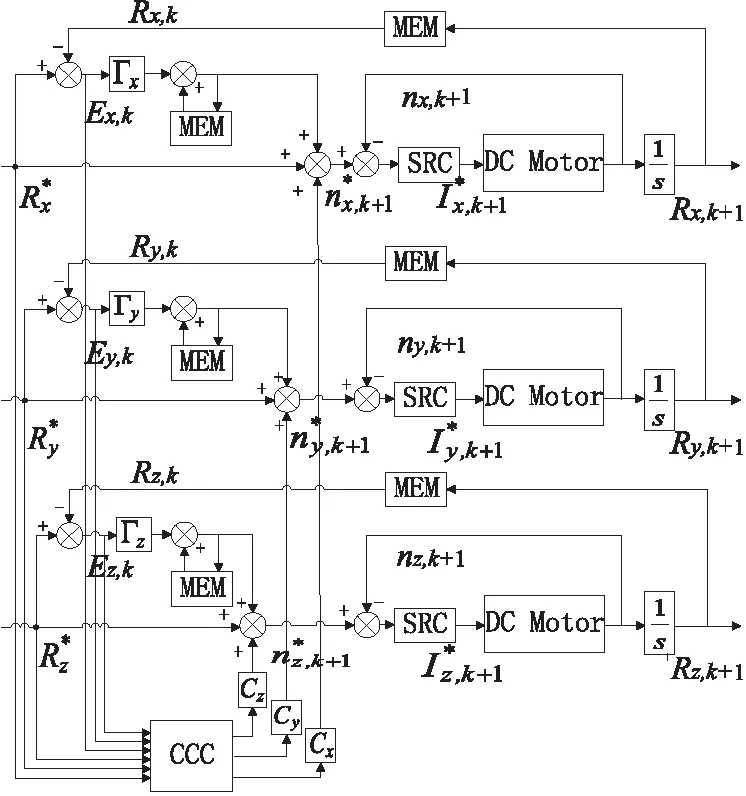
图3 迭代滑模交叉耦合控制器结构简图

对于单轴电机，设计速度环滑模控制器，可以抑制非周期干扰；设计位置环迭代学习控制器，能够抑制周期性干扰和减小单轴跟踪误差。对于三轴电机，设计轴间变增益交叉耦合控制器，用以减小系统的轮廓误差。

3.1 速度环滑模控制器的设计

滑模控制(Sliding Mode Control, SMC)是一种具有强鲁棒性的非线性控制方法，通过控制量的切换使系统状态沿着滑模面滑动，会产生抖振，不适合作为位置环控制器，因此将其设计为速度环控制器，用以抑制非周期干扰[7]。

由于直流电机的电流变化率很小，现忽略项

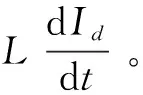
Ua=RId+Cen

(17)

联立式(10)、式(12)和式(17)，合并并消去Id和Te，可得：

(18)

移项整理，得：

(19)

设状态变量x=n*-n，将n=n*-x代入式(19)中，可得系统的状态方程为：

(20)

取PI型滑模面：

(21)

对式(21)求导，可得：

(22)

(23)

化简，可得系统的等效控制律为：

(24)

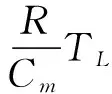
(25)

3.2 轴间变增益交叉耦合控制器的设计

交叉耦合控制器有演算轮廓误差和将其分别补偿到各轴的作用[9]。在位置回路中添加交叉耦合控制器，如图3所示，构成完整的控制系统。

第1节已详细介绍了如何估计空间轮廓误差，根据空间轮廓误差ε的表达式(8)，得到轮廓误差补偿量C为：

C=Cxεx+Cyεy+Czεz

(26)

式中，Cx、Cy和Cz分别为各轴的交叉耦合增益值，能够影响轮廓误差的修正速度。

3.3 位置环迭代学习控制器的设计

迭代学习控制(Iterative Learning Control, ILC)具有高精度的跟踪性能，利用系统先前的控制经验，不断修正系统控制量，寻求一个理想的输入特性曲线，使被控对象产生期望运动[10]。

对于X轴，它的跟随误差为：

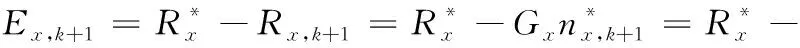
(27)

同理，Y轴和Z轴的跟随分别误差为：

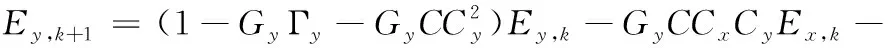
(28)

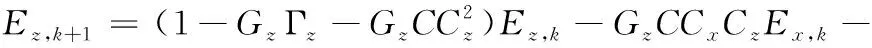
(29)

(30)

对式(30)取范数，得：

(31)

根据迭代学习控制的收敛条件，可得：

(32)

由此可见，求解满足上式条件的迭代学习律和交叉耦合控制器，使得迭代收敛，系统能够最终稳定。

4 仿真结果及分析

采用三台相同的直流电机作为直角坐标机器人的驱动部件进行仿真研究，电机的参数如表1所示。

表1 台鸿50SYX01直流电机参数说明

机器人的期望跟踪轨迹为空间螺旋线，方程为：

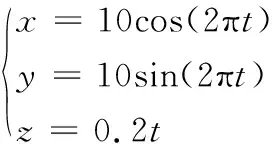
(33)

对所设计的迭代滑模交叉耦合控制器进行验证，图4为直角坐标机器人期望轨迹与实际输出轨迹，可以明显看出，两者基本重合，所设计的控制器性能良好。为验证速度环滑模控制、位置环迭代学习控制的优越性，将分别单独测试其性能：

首先，比较速度环SMC和普通PID控制在抑制非周期干扰方面的性能，结果如图5所示。以y轴为例，y轴转速跟踪的是周期为1s，幅值为568rpm的余弦波。电机空载运行后，PID控制需要将近0.1s进入稳态，而SMC很快进入稳态；在0.5s给电机加10N的负载，PID的动态响应能力较弱，而SMC体现出很强的抗干扰能力。

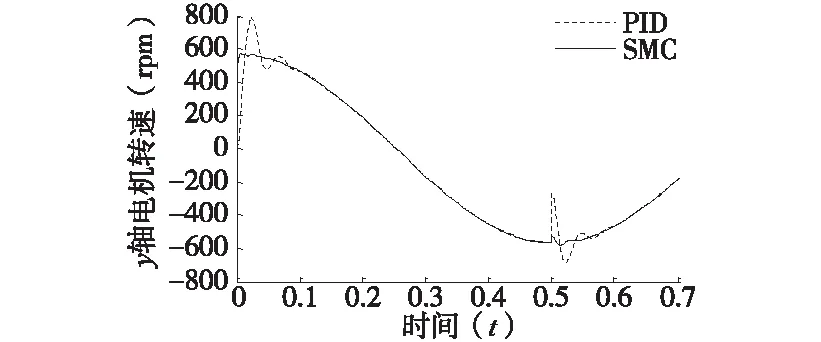
图5 y轴负载变化时速度环SMC与PID的对比

然后，比较位置环ILC和普通PID控制在位置跟踪方面的性能，结果如图6所示。以x轴为例，x轴位置跟踪的是周期为1s，幅值为100mm的余弦波。PID控制能够使位置跟踪误差迅速收敛，但是由于没有学习能力，重复运行并不能改善系统性能，位置误差峰峰值始终保持在±0.62mm；采用ILC，系统运行到第2秒，即迭代学习进行了2次后，位置误差逐渐减小，最终峰峰值收敛于±0.08mm，以此验证了ILC具有高精度的跟踪性能。

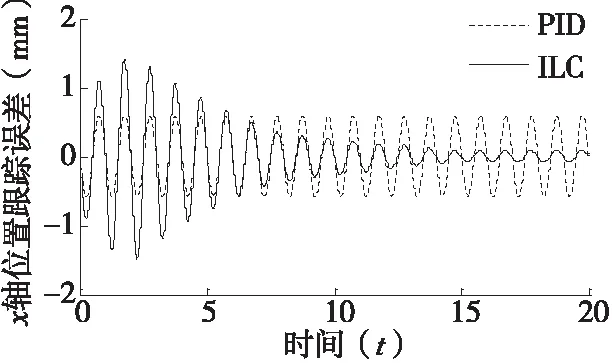
图6 x轴位置环ILC与PID跟踪误差的对比

最后，比较迭代滑模交叉耦合控制器与普通交叉耦合控制器在控制轮廓误差方面的性能，结果如图7所示。在ILC+SMC+CCC控制下，系统具有学习能力，轮廓误差不断减少，经过6次迭代后，已经小于普通CCC控制下的轮廓误差，随着迭代次数的增加，最终轮廓误差被控制在0.04mm。可见，采用LC+SMC+CCCI控制可以有效地补偿轮廓误差。

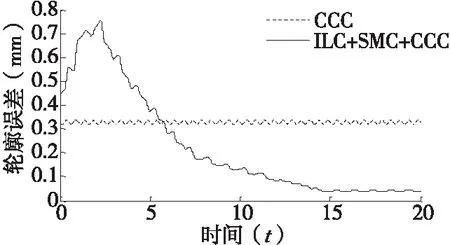
图7 ILC+SMC+CCC与CCC轮廓误差的对比

5 结论

针对直角坐标机器人，本文设计了一种迭代滑模交叉耦合控制器。单轴速度环采用滑模控制，能有效抑制系统的非周期干扰；位置环采用迭代学习控制，具有高精度的跟踪性能；轴间采用变增益交叉耦合控制器，能演算并补偿轮廓误差。仿真结果表明，所设计的迭代滑模交叉耦合控制器能大幅度提高直角坐标机器人的轮廓精度和鲁棒性。

[参考文献]

[1] 孟明辉, 周传德, 陈礼彬,等. 工业机器人的研发及应用综述[J]. 上海交通大学学报, 2016(S1):98-101.

[2] Ramesh R, Mannan M A, Poo A N. Tracking and contour error control in CNC servo systems[J]. International Journal of Machine Tools & Manufacture, 2005, 45(3):301-326.

[3] Wang J, Liang H, Guan D G, et al. Contour error and control algorithm in CNC machining tool[C]// International Conference on Mechatronics and Automation, IEEE, 2012:2351-2355.

[4] 赵希梅, 郭庆鼎. 基于ZPETC和CCC的直驱XY平台高精度控制[J]. 组合机床与自动化加工技术, 2011(2):83-85.

[5] 魏代海, 邓开发, 吴承刚,等. X-Y平面3D打印的交叉耦合矢量控制研究[J]. 包装工程, 2014(11):118-121,127.

[6] Wang J, Liang H, Guan D G, et al. Contour error and control algorithm in CNC machining tool[C]// International Conference on Mechatronics and Automation ,IEEE, 2012:2351-2355.

[7] 蔺威威. 三轴运动平台精密轮廓控制方法研究[D]. 沈阳:沈阳工业大学, 2016.

[8] 陈伯时. 电力拖动自动控制系统 : 运动控制系统[M].北京:机械工业出版社, 2003.

[9] 罗志伟, 谷爱昱, 洪俊杰,等. 基于改进型速度滑模控制器的永磁直线同步电机伺服系统[J]. 电机与控制应用, 2016, 43(12):39-43.

[10] 杜智超. 伺服系统滑模控制与干扰抑制[D]. 北京:北京理工大学, 2016.

[11] 彭宝营, 蔡力钢, 韩秋实,等. 非圆曲面XY直驱加工廓形误差交叉耦合控制[J]. 计算机集成制造系统, 2014, 20(3):618-626.

[12] 周延松, 于飞, 徐建明,等. 串级型迭代学习交叉耦合轮廓误差控制方法[J]. 科技通报, 2011, 27(5):737-739.