主成分分析法应用中原始数据的标准化辨析

魏登云, 张文俊

(安徽师范大学 体育学院，安徽 芜湖 241003)

导 言

主成分分析法作为多元统计分析最常用的方法之一，在体育领域中有着最广泛的直接或间接的应用。以协方差矩阵的特征值和特征向量为基础(工具)，使主成分的计算问题得以彻底解决，但与此同时也在一定程度上掩盖了主成分分析的直观思想，容易导致主成分分析法的应用程序化，一旦实际问题特殊，研究目的不同，在某些细节的处理上，对计算结果的运用上，应用者可能会产生迷茫和偏差，例如在体育综合评价中，运用主成分分析法赋权；主成分分析中的优势效应和因子遗漏现象；认知数据的主成分与因子分析等，都很容易导致错误的结果，文献[1-3]对上述问题均有比较具体的讨论。除此之外，一个更值得关注甚至是亟待解决的问题是，主成分分析法应用中原始数据的标准化问题。原始数据的标准化处理(减去平均数，再除以标准差)，被视为无量纲化的常用手段，当遇到量纲不同的数据时，人们往往首先想到的是对数据进行标准化处理[4-7]。实际上，标准化处理改变了相应变量的均值和方差信息，因而对某些统计方法的运用结果产生很大影响，主成分分析法就是对标准化处理最为敏感的一种，基于原始数据得到的主成分与标准化数据的主成分往往大相径庭，在此基础上的主成分分析结果也大不相同。那么，原始数据的标准化处理对主成分分析究竟有何影响？主成分分析法应用中如何对待原始数据的标准化问题，即何时应该对数据标准化，何种情况下不能标准化？此类问题至今没有解决。

本文拟从理论上论证原始数据的标准化处理对主成分分析的具体影响，结合实际工作中运用主成分分析的目的，讨论数据标准化的使用策略。

1 原始数据的标准化对主成分分析的影响

从对某种统计方法的影响来看，原始数据的标准化与原始变量的标准化本质上是一回事。为了便于在总体层面阐述，以下讨论均针对变量的标准化。

1.1 原始变量与标准化变量的主成分大相径庭

不难发现，标准化处理不仅仅是无量纲化处理的一种手段，同时也改变了原始变量的均值和方差信息，尤其是方差，各个原始变量的方差大小可能多种多样，但所有标准化变量的方差大小均是一样的。这对于以分析变异为根本手段的主成分分析来说，无疑是改变了研究对象，基于原始数据的主成分分析是研究原始变量的主成分，而基于标准化数据的主成分分析则是分析标准化变量的主成分。鉴于变量的方差大小对主成分的影响，可想而知，原始变量与标准化变量的主成分大不相同，就是必然的。看一个具体例子。

例1设三个变量X1,X2,X3的协方差矩阵为

经计算，变量X1,X2,X3的三个主成分及其方差分别为

y1=X3,λ1=25

y2=0.992X1+0.130X2，λ2=16.262

y3=-0.130X1+0.992X2,λ3=0.738

标准化变量Z1,Z2,Z3的协方差矩阵(相关系数矩阵)为

经计算，标准化变量Z1,Z2,Z3的三个主成分及其方差分别为

W1=0.707Z1+0.707Z2,δ1=1.5

W2=Z3，δ2=1

W3=-0.707Z1+0.707Z2，δ3=0.5

对比两组主成分，可以看出，原始变量与标准化变量的主成分大不相同。无论是主成分的顺序、主成分方差，还是主成分系数都大相径庭，而且可以设想，如果不改变变量X1,X2,X3之间的相关关系，任意改变三个变量的方差大小，则变量X1,X2,X3的主成分多种多样，而标准化变量的主成分却是不变的。这也说明原始变量的主成分不仅与标准化变量大不一样，而且二者之间没有也不可能有特定的关系使其可以相互导出。

1.2 原始变量与标准化变量的主成分含义

既然标准化处理导致主成分“面目全非”，那么，一个自然的问题是：主成分分析应用中，原始数据是否不能标准化？或者必须标准化？为此，我们通过分析变异，解释原始变量和标准化变量的主成分所承载的信息，讨论基于原始变量和标准化变量的主成分分析在应用中的优缺点。

原始变量的主成分主要描述大方差变量的主要变异和变量之间的同质变异，解释变量的方差信息和变量之间的相关关系信息，由于大方差变量在主成分形成过程中的优势地位，少数几个甚至一个大方差变量有时就构成一个主成分，甚至是第一主成分(如例1中的X3)，所以当各个变量的方差相差较大时，原始变量的主成分可能更多地解释了大方差变量的方差信息，这在主成分系数上可以看出来，大方差变量总会在某个主成分中具有较大的系数。但是，如果变量的量纲不同，各个变量的方差大小不具有可比性，基于原始变量的主成分分析将失去意义。主成分分析的本意是用少数几个主成分描述总变异，方差只是变异大小的一种度量，方差有量纲，如果原始变量的量纲不同，那么大方差变量未必有较大的变异，所以基于不同量纲的原始变量的主成分未必描述了“主要变异”。这是基于原始变量的主成分分析所面临的最突出的问题。

标准化变量的主成分描述一组标准化变量的主要变异，由于每个标准化变量的方差均为1，每个标准化变量的地位均等，所以标准化变量的主成分，尤其是第一主成分，主要描述同质变异的大小，解释一组标准化变量内部的相关关系。如果第一主成分方差很大，说明在这组标准化变量中有很多高度相关的变量，如果第一主成分方差较小，则说明该组变量内部没有多少相关关系。由于标准化处理不改变变量之间的关系，原始变量内部的相关关系信息与标准化变量一致，所以也可以说，标准化变量的主成分解释了原始变量内部的相关关系。这正是标准化变量主成分最突出的优点，也是标准化变量与原始变量的主成分的最本质的区别，原始变量的主成分尽管也考虑变量之间的关系，但是受到各个变量方差大小的严重干扰，其主成分很难分析变量之间的复杂关系。

标准化变量的主成分系数反映变量的相关性优势，如果某几个标准化变量在某个主成分中有较大系数，则说明该主成分描述的是以这些变量为代表的同质变异，解释了这些变量之间共同的东西。实际应用中，人们一般不会在意某一个标准化变量的主成分系数的具体大小，而是关注在某个主成分中，哪些变量的系数相对较大，从而便于解释该主成分所描述的个体特征。这与原始变量的主成分不同，原始变量的主成分分析可能在考虑同质变异的同时，更关注某一个变量的主成分系数大小，因为如果某个变量的系数较大，说明该主成分可能描述了该变量的主要变异。基于标准化变量的主成分分析不考虑各个变量的个别差异，而是要分析一组变量中有哪些相关优势群，并以相应的主成分来代表。由此看来，基于原始变量和标准化变量的主成分分析的目的是不一样的，原始变量的主成分代表了一组变量的主要变异，而标准化变量的主成分则象征着几个主要的相关变量群。例1中，原始变量的两个主成分y1和y2分别描述了以X3和X1为代表的主要变异，而标准化变量的两个主成分W1和W3则代表着(X1,X2)和X3两个变量群。

值得一提的是，由于原始变量的量纲不同，有人在应用中先对原始数据标准化，得到标准化变量的主成分，再将其中的标准化变量还原成原始变量，分析原始变量对主成分的贡献，解释主成分。应该说，这样做是不可以的。我们以例1为例来说明。标准化变量的第一主成分W1=0.707Z1+0.707Z2，将Z1和Z2还原成原始变量后，得到

(1)

如果以此分析变量对主成分的贡献，那么X2对第一主成分的贡献最大，X1次之，X3对第一主成分没有贡献。对比原始变量的主成分，变量X3对第一主成分的贡献最大，而X1和X2对第一主成分没有贡献，结果截然不同。从变量组X1,X2,X3的相关关系看，X1与X2相关，X3与X1和X2均不相关，所以(Z1,Z2)和Z3分别构成两个相关变量群，Z1和Z2组成了相关优势变量群。即使将Z1和Z2还原成原始变量，但W1依然是标准化变量的主成分，代表的依然是相关优势变量群(X1,X2)，其中X1和X2地位均等。(1)式中X1和X2的系数0.177和0.707分别是X1和X2的标准差的倍数，形式不同而已。

2 主成分分析法应用中原始数据的标准化策略

以上讨论表明，原始数据的标准化处理，不仅仅是无量纲化处理，它改变了变量的均值和方差信息，不知不觉中已经改变了主成分分析的对象，影响主成分的生成和取舍。从研究目的来看，基于原始变量的主成分分析，在考虑变量之间关系的同时，可能更关注各个变量的方差；而基于标准化变量的主成分分析，则只考虑变量之间的关系，各个变量的地位被视为均等。所以在主成分分析法应用中，原始数据是否应该标准化，要视实际问题的具体研究目的而定。宏观上说，如果实际问题的分析，需要保留或借助各个变量的变异信息，则原始数据不能标准化；如果研究目的只需要变量之间的相关关系信息，不需要各个变量的变异大小，那么在作主成分分析时，原始数据必须标准化。以下我们在相对具体的层面，阐述主成分分析法应用中原始数据是否应该标准化的问题。

2.1 主成分分析法用于描述总体

体育科研中，经常需要描述总体的有关特征，如总体的分布特征、均值状况以及总体内个体之间的差异情况，有时由于涉及的变量很多，需要简化、压缩数据，主成分分析法通常是变量压缩的首选方法。但是在作主成分分析时，原始数据不能标准化。因为描述总体的特征需要变量的均值、方差甚至极值等信息，如果对原始数据标准化，那么变量的有关重要信息就没有了，在此基础上作主成分分析得到的主成分是标准化变量的主成分，课题研究目的所需要的很多信息均已失去，因此达不到研究目的。

但是，实际问题中多个变量的量纲不同，很多统计指标不具有可比性，如均值、方差等，而主成分分析对各个变量的方差大小又非常敏感，所以可能需要对原始数据作无量纲化处理。无量纲化处理的方法有多种，除了标准化处理之外，还有原始数据除以平均数、原始数据除以极值等手段。一般来说，对原始数据作任何一种处理，都会改变某些数据信息，至于选择哪一种无量纲化处理方法，要根据研究目的来确定。原始数据除以平均数，改变了数据的均值信息，但保留了数据的变异信息，经其处理后的数据方差实际上是原始数据的变异系数，这种无量纲化处理对主成分分析结果没有不利影响，所以在运用主成分分析法描述总体的变异特征时，原始数据除以平均数是一种比较合适的无量纲化处理方法。

2.2 主成分方法用于一组变量的因子分析

因子分析的实质是用少数几个潜在的不能观测的公共因子去描述一组变量内部的相关关系，常被称作是主成分分析的一种延续。因子分析的主要工作之一是对因子载荷矩阵和特殊方差的估计，而主成分方法是因子分析中估计因子载荷矩阵和特殊方差的两种常用方法之一(另一种是极大似然法)。众所周知，正交因子模型

X-μ=LF+ε

(2)

的协方差结构为

∑=LL′+ψ

(3)

(3)式通常被称为协方差矩阵∑的因子化分解。主成分方法估计因子载荷矩阵L和特殊方差矩阵ψ的做法是，基于协方差矩阵∑的谱分解，得到∑的近似因子化分解，因子载荷矩阵

(4)

其中(λi,ei)(i=1,2,…,m)是∑的前几个特征值和特征向量对[8]。由样本协方差矩阵S可以得到L的估计量

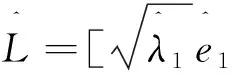
(5)

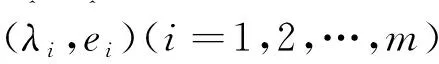
可见，由主成分方法得到的因子载荷阵的估计量完全取决于样本协方差阵S的特征值和特征向量。

由模型(2)可见，标准化变量Z满足

(6)

因子分析的目的，是基于变量之间的相关关系，解释一组变量内部的公共因子，所以因子分析的结果不应该受变量方差大小的影响，否则，大方差变量(未必是公共因子)容易生成公共因子，势必会影响公共因子的取舍，从而排挤真正的公共因子，导致公共因子的遗漏。因此，在运用主成分方法作因子分析时，原始数据应该做标准化处理。

2.3 主成分方法用于分析一组变量对响应变量的影响

分析一组变量对响应变量的影响，最典型的统计方法就是回归分析。在回归分析中，由于预测变量之间经常存在共线性关系，从而严重影响最小二乘估计量的精度和回归系数估计值的稳定性，克服共线性影响的常用方法就是以预测变量的主成分为自变量作回归分析，称作主成分回归[9]。应该说，回归分析本身对原始数据是否标准化没有要求，无论是基于原始数据还是标准化数据，回归方程的效果不受影响。但是，对于主成分回归，情况却不一样。由于预测变量的主成分的生成和取舍受各个预测变量方差大小的影响，所以基于原始数据和标准化数据的主成分回归可能在“自变量”(主成分)的选择或者取舍上存在很大的不同，导致回归分析的结果不一样。

我们知道，分析一组变量对响应变量的影响，需要的是一组预测变量与响应变量之间关系的信息，预测变量的方差大小不应该影响分析的结果，大方差预测变量有可能对响应变量没有什么影响，而小方差变量也可能对响应变量有很大影响。然而，由于主成分分析“眷顾”大方差变量，所以在主成分回归中，可能对响应变量有很大影响的小方差变量，其地位和作用在主成分分析环节中被弱化，而对响应变量影响较小的大方差变量，其地位和作用在无意中被强化了，从而会影响回归方程的效果。如果对原始数据作标准化处理，则可避免变量方差大小对分析过程的干扰。因此，如果运用主成分方法分析一组变量对响应变量的影响，建议对原始数据作标准化处理。

2.4 主成分分析法用于体育综合评价

就主成分分析或主成分因子分析在体育综合评价中的应用现状来看，主成分分析法主要用于评价指标的压缩和权重系数的确定。初选的评价指标通常数目众多，而且指标之间难免有较多的信息重叠，所以往往需要对评价指标进行压缩，将众多的原始评价指标压缩成少数几个互不相关的新评价指标，这些新评价指标要求对原始评价指标有代表性，即，新评价指标要能够基本涵盖原始评价指标所描述的多种主要特征。对此，主成分分析或因子分析法是常用的方法。但是，运用主成分方法所得到的新评价指标(即主成分)，对原始评价指标的代表性受原始指标的方差大小影响，如果原始评价指标没有经过标准化处理，那么在生成新评价指标的过程中，大方差指标会“排挤”其他的评价指标，影响新评价指标的取舍，造成某些因子的遗漏。事实上，一组变量的主成分对变量组的代表性，取决于变量之间的关系，如果变量之间均高度相关，那么少数几个甚至一个主成分就可以代表一组变量，而与变量的方差大小无关。所以，在运用主成分分析法(或主成分因子分析法)对评价指标进行简化、压缩的时候，原始数据需要作标准化处理。

在体育综合评价中，也有部分文献运用主成分分析法确定权重系数(文献[1]中做过统计)，最有代表性的做法是：对标准化评价指标Z1,Z2,…,ZP作主成分分析，选取前若干个主成分y1,y2,…,ym，以各个主成分的方差贡献率gi(i=1,2,…,m)作为权重系数，建立综合评价模型

(7)

其中

(8)

3 小 结

综上所述，主成分分析是对一组变量的分析，变量的标准化，不改变变量之间的关系，但改变了变量的方差，所以原始变量的主成分与标准化变量的主成分不仅不大一样，而且不能相互导出。对原始数据作标准化处理，实质上是改变了主成分分析的对象和目的，基于原始数据和基于标准化数据所得到的主成分的含义也不大相同。在主成分分析法应用中，如果研究目的需要保留变量的变异信息，则原始数据不能标准化，但可以作无量纲化处理，例如主成分分析法用于描述总体；如果研究目的只需要变量之间的关系信息，不关心各个变量的变异大小，则原始数据需要标准化，例如主成分分析法用于主成分回归、因子分析以及体育综合评价时，原始数据需要作标准化处理。

参考文献:

[1] 赵书祥.我国体育领域中综合评价理论与方法及实证的研究[D].北京：北京体育大学，2008.

[2] 魏登云.主成分与因子分析在体育综合评价中的应用检测[J].体育科学，2003,25(4):97-99.

[3] 朱晓峰，魏登云.体育科研中对认知数据主成分分析与因子分析的再认识[J].体育科学,2008,28(6):73-77.

[4] 张卫华，赵铭军.指标无量纲化方法对综合评价结果可靠性的影响及其实证分析[J].统计与信息论坛，2005，20(3)：33-36.

[5] 郭亚军，易平涛.线性无量纲化方法的性质分析[J].统计研究，2008，25(2)：93-100..

[6] 张立军，袁能文.线性综合评价模型中指标标准化方法的比较与选择[J].统计与信息论坛，2010，25(8)：10-15.

[7] 叶宗裕.关于多指标综合评价中指标正向化和无量纲化方法的选择[J].浙江统计，2003(4)：24-25.

[8] JOHNSON R A，WICHERN D W.实用多元统计分析[M].陆璇等,译.北京:清华大学出版社,2001.

[9] 陈希孺，王松桂.近代回归分析——原理方法及应用[M].合肥：安徽教育出版社，1987.