从一道高考题探究分析函数零点问题的基本方法

广东省汕头市澄海中学 李立峰

函数零点是函数知识的一个重要内容，是高考考查的热点之一，本文主要从一道高考题探究分析解决函数零点问题的基本方法。

引例（2017年全国卷Ⅰ理科第21题）：已知函数（a-2）ex-x。

（1）讨论 的单调性；

（2）若 有两个零点，求a的取值范围。

（注：本题是高考题，这里不再详述其解题过程）

从教材函数零点的知识我们不难看出，函数的零点、方程的根，函数图象与坐标轴的交点这三个不同的数学概念常统一在一起，它们有区别，但更多时候是密不可分的，从中我们可以得出分析函数零点问题的三种思路：

1.解方程，由方程 的根得函数 的零点。

2.利用函数单调性结合零点存在性定理。

3.数形结合法，根据题目的函数、方程，运用转化与化归的数学思想，通过分离参数法、作差法、拆分法等构造函数，再结合函数的图象分析问题。例1 函数的零点为____________。

分析：都是R上的增函数，

R上也是增函数。

又

函数的零点为x=2。

对于这类超越函数的零点问题，由于高中教材知识的限制，因此一般通过观察与分析，利用特殊值代入法结合函数单调性求解。

例1这类问题用到思路1，通过寻找方程 的根得到函数的零点，具体操作中一般借助分解因式或者特殊值代入法。

例2 已知函数g（x）＝2lnx－x2＋上有两个零点，求实数m的取值范围。

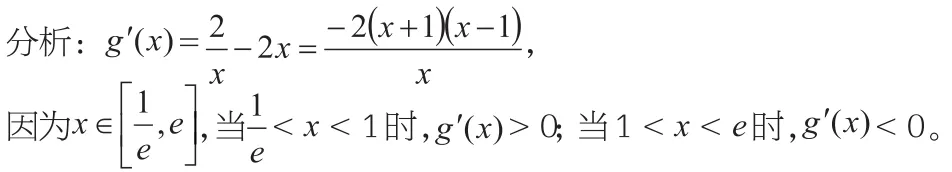
故g(x)在x=1处取得极大值，即最大值g（1）=m-1。

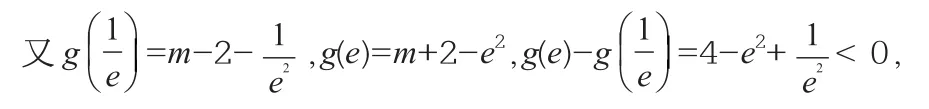
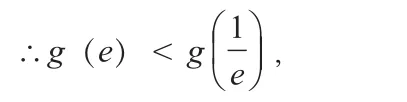
所以g（x）在上的最小值是g（e），

故g（x）在上有两个零点等价于

解得1＜m≤2+所以实数m的取值范围是

本题用到思路2，利用函数单调性与零点存在性定理，结合函数的极值、最值，分析函数的零点，这是最常用的方法，引例及2016年全国新课标Ⅰ卷理科第21题均用到此法。

例3 设（e为自然对数的底数），若关于x的函数有且仅有6个零点，则实数a的取值范围是（ ）

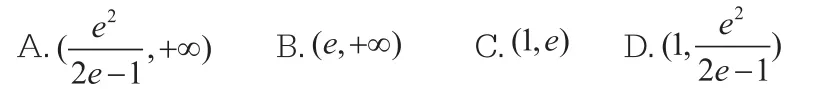
令

由

得

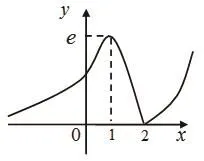
故 的大致图象如右图：

方程在上有两个不同的解时可以满足题意，

令

则故选D。

“数缺形时少直观，形少数时难入微”，本题用到思路3，利用数形结合法解决问题。本题运用转化与化归的数学思想与换元法，构造函数 ，利用其导数画出函数的草图，再借助其图象辅助分析问题。注意在画草图时，不仅要考虑函数的单调性和极值，还要研究函数在区间端点的函数值情况。

虽然函数零点问题是一个难点，但只要我们理解好三种解题思路的精髓，充分利用好导数这个工具，注意题型的归纳和积累，多运用转化与化归思想、数形结合法和换元法等数学思想与方法，克服恐惧心理，大胆尝试，我们就一定能提高此类题目的得分率。

[1]陈祥国.函数压轴寻常见导数应用有情结[J].中学数学教学参考，2016（5）：51-53.

[2]王秀彩.导数的综合应用[J].中学数学教学参考，2016（1-2）：124-128.