基于一道高考题的解法探讨及对物理教学的启示

刘 秀

(安徽省阜阳市第三中学 236000)

2014年我国教育部发布的教育部《关于全面深化课程改革 落实立德树人根本任务的意见》指出“在基础教育阶段应该帮助学生形成适应个人终身发展和社会发展需要必备品格和解决问题的素养和关键能力，立德树人.”基础教育的目的在于落实立德树人的根本任务. 2017年物理全国卷1第21题以日常学生较为熟悉热点问题“力学中的动态平衡问题”为背景，但突破了力学态平衡问题较为常见的“已知合力和其中一个分力方向，研究在另一个分力发生变化时，两分力大小如何变化”适度创新演化成“合力级两分力的夹角不变同时旋转两分力方向的问题”，令不少学生感觉到很棘手.高考由知识立意向能力立意、素养立意的转化，对学生的物理观念和科学思维有较高的要求.是一道熟悉的创新的亮点题.

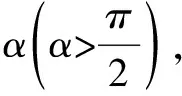
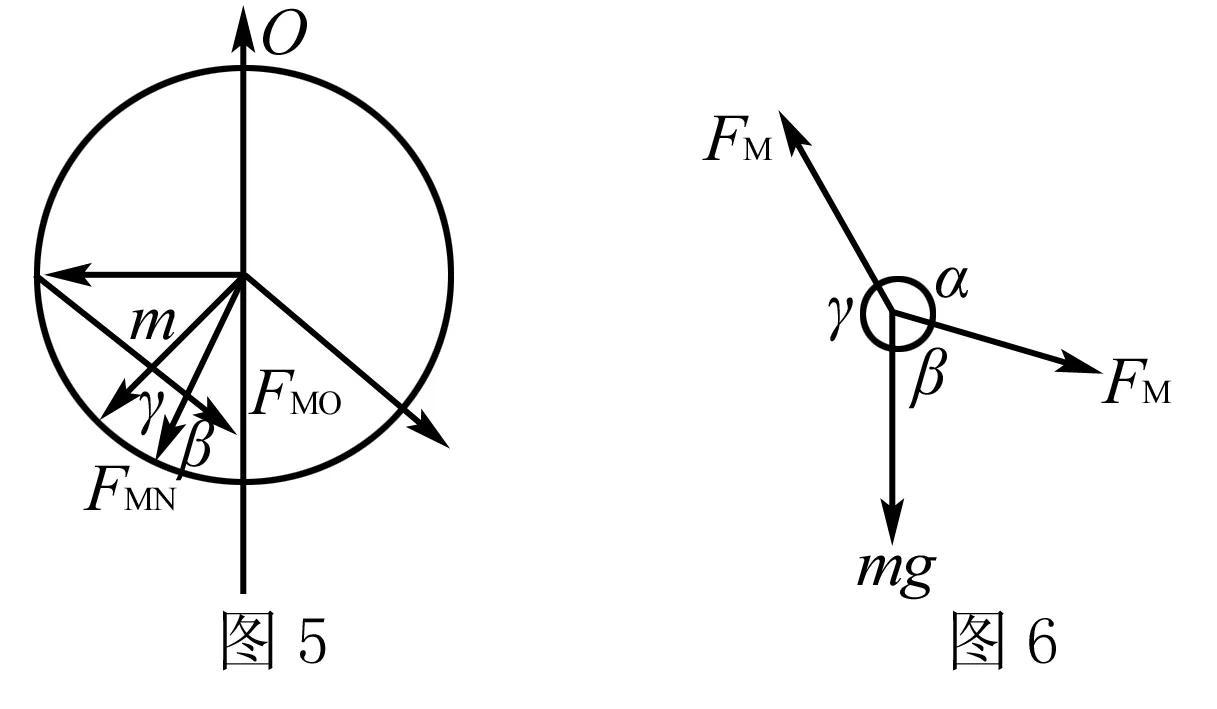
B．MN上的张力先增大后减小

C．OM上的张力逐渐增大

D．OM上的张力先增大后减小

解析解法一(平行四边形)矢量三角形法

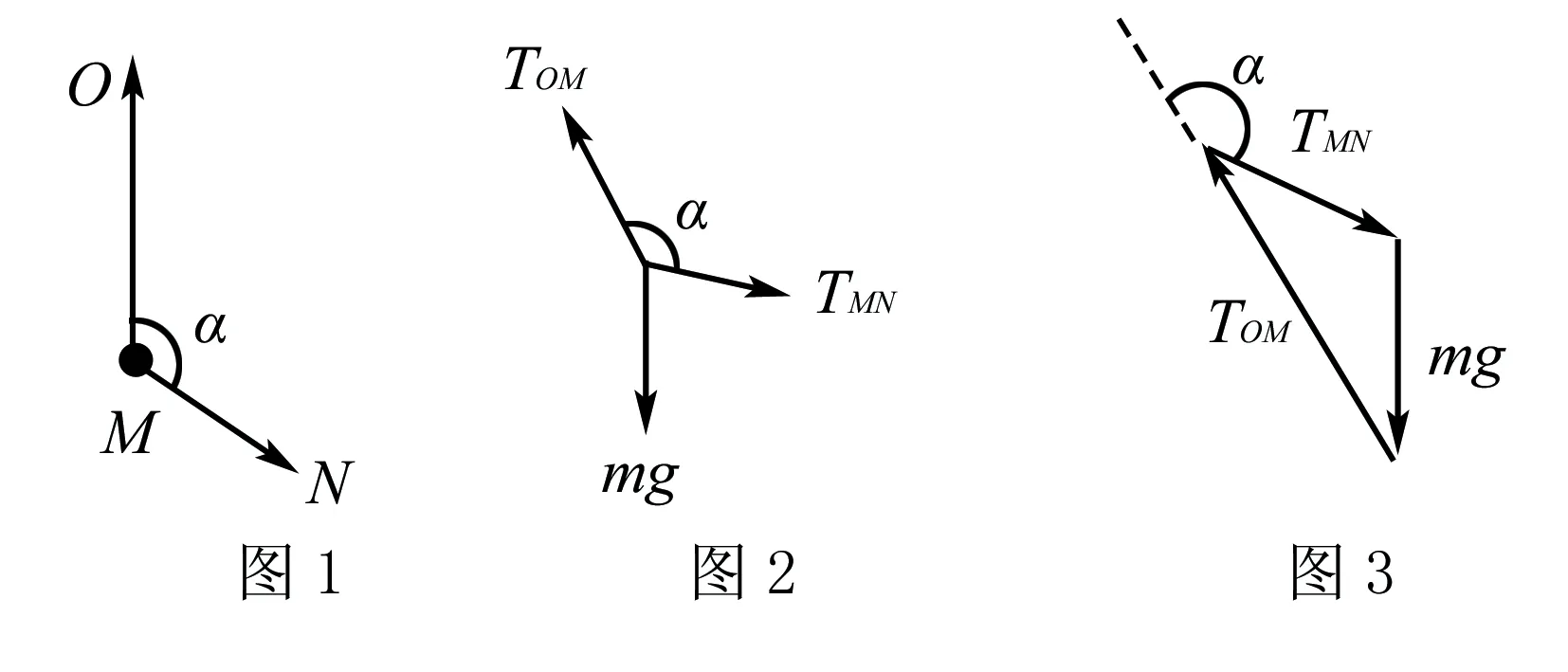
由题意可知，重物在运动过程中受重力，MN绳拉力TMN，OM绳拉力TOM，TMN与TOM夹角保持不变.在某一时刻三个力受力分析示意图如图2所示，将此三个力平移为矢量三角形如图3所示.因为mg大小方向不变.TMN与TOM的夹角不变，故可将三个力平移入圆中如图4，mg为一条固定的弦(固定的弦所对应的圆周角为定值).由图4可得TMN从0逐渐变为直径，故TMN逐渐增大，A对B错，TOM先从弦变为直径再变为弦，故TOM先变大后变小，C错D对，故选AD.

解法二等效法

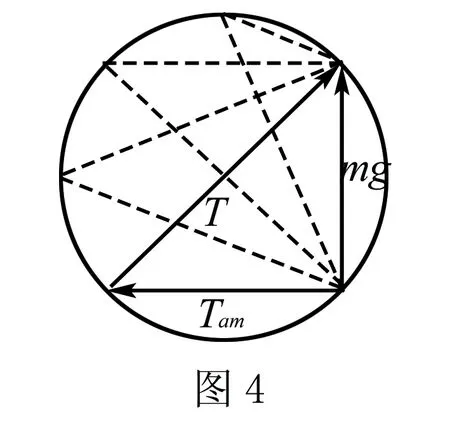
重物在受重力mg，MO绳拉力FMO,MN绳的拉力FMN，FMO和FMN夹角保持不变方向在逆时针转动90°的过程中根据等效法视为FMO和FMN方向不变，重力mg的方向顺时针旋转90°.作矢量三角形图如图5所示，在旋转过程中MO绳拉力FMO先增大后减小，在β=90°(FMO与圆相切即重力方向垂直时)值最大.MN绳的拉力FMN逐渐增大.

解法三(正弦定理)拉密定理

二、解法评析

本题的各种不同的解法中明显共同的特征就是数学性，用数学思想思考、分析、解决物理问题，如：解法一中根据夹角不变巧妙建立辅助圆，解法三中运用拉密定理等考纲中对“运用数学知识解决物理问题能力”考查，体现了数学和物理的密切联系，凸显数学思维的丰富特性,到落实《考试大纲》和反映新课改理念.

教学启示 基于上述分析研究，在高中物理教学中，要结合教育部提出“在基础教育阶段应该帮助学生形成适应个人终身发展和社会发展需要必备品格和解决问题的素养和关键能力，立德树人” 通过教学帮助学生形成物理学科核心素养.”教学采取如下目标定位：(1)教学中构建教学情境，培养学生的实践意识，培养运用物理知识处理实际、运用数学知识解决物理问题的能力.(2)通过启发式提问和研讨式教学培养学生强烈的问题意识，邦之学生逐步形成物理观念建立科学的思维方式.(3)加强高阶思维能力的训练.通过问题情境的建构和布置有一定深度的问题求解任务，激发学生的求解欲望，使学生把分析、评价、创造自觉运用到问题求解的过程中，从思维提升的角度发展高阶思维能力.

参考文献：

[1]邵忠奎，都兴男.一道力学动态平衡问题巧解[J].中学物理，2016(2)87-87.

[2]顾祖恩.教学情境设计[M].上海：上海科技教育出版社，2013.

[3]林勤.思维的跃迁[M].上海：华东师范大学出版社，2016:4-5.