带电粒子在三种场重叠区域的运动

张大洪

(重庆市潼南第二中学 402660)

带电粒子在重力场、匀强电场、匀强磁场共存的重叠场中运动时，由于重力场、匀强电场对带电粒子的作用力均为恒力，匀强磁场对带电粒子的洛仑兹力f=qvB⊥与粒子速度v成正比，故随粒子速度v的大小、方向的变化其受到的合力大小、方向均可能发生相应变化，因而粒子的运动情况也会随之改变，这将使问题的处理与解答变得更为困难；本文从实例的处理入手加以总结，归纳分析处理此类问题的思路与方法.

一、带电粒子在三种场重叠区域中作无约束的直线运动、圆周运动问题的分析

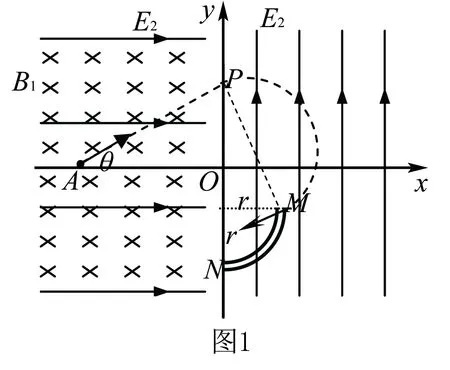
例1 如图1示在一竖直平面内，y轴左方有一水平向右的场强为E1的匀强电场和垂直于纸面向里的磁感应强度为B1的匀强磁场，y轴右方有一竖直向上的场强为E2的匀强电场和另一磁感应强度为B2(大小、方向均未知)的匀强磁场.有一带电荷量为+q、质量为m的微粒，从x轴上的A点以初速度v与水平方向成θ角沿直线运动到y轴上的P点，A点到坐标原点O的距离为d.微粒进入y轴右侧后在竖直面内做圆周运动，然后以与P点运动速度相反的方向打到半径为r的四分之一绝缘光滑圆管内壁的M点(假设微粒与M点碰后不反弹、电荷量不变，圆管内径的大小可忽略，电场和磁场不受影响地穿透圆管)，并沿管内壁下滑至N点，设m、q、v、d、r已知，θ=37°，sin370=0.6、cos370=0.8，求：

(1)电场强度E1与E2的大小之比？

(2)y轴右侧磁场的磁感应强度B2的大小、方向？

(3)微粒从A点运动到N点所用的时间？

解析(1)微粒沿AP直线运动中其受力右图1-1示，由于洛仑兹力大小随粒子运动速度的变化将发生相应变化而重力、电场力为恒力，故合力将随粒子运动速度而变化；要使粒子作直线运动则只有让洛仑兹力恒定即其速度恒定不变，故粒子必作匀速直线运动；因而图中三力之合必为0即有qE1cosθ=mgsinθ…①；

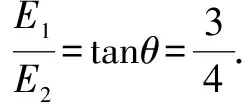
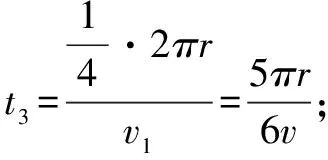
总结：带电粒子在三种场重叠的区域内在无其它约束情况下：

1.粒子作直线运动时——只能作匀速直线运动，故三场力之合必为0；

2.粒子在竖直平面内作圆周运动时:粒子受到的电场力与重力必等大、反向、共线即此二力平衡，粒子只在洛仑兹力作用下作匀速圆周运动，即洛仑兹力作向心力；

练习1 如图1-2甲所示，虚线间空间存在由匀强电场E和匀强磁场B组成的正交或平行的电场和磁场，有一个带正电小球(电荷量为+q，质量为m)从正交或平行的电磁混合场上方的某一高度自由落下，那么，带电小球可能沿直线通过下列的哪个电磁混合场( ).

解析在四种情况中带电小球进入复合场时受力情况如图1-2乙所示：A图中由于小球所受合力不为零，所以洛伦兹力不恒定，因此水平方向合力不可能保持为零，小球不可能沿直线运动；B图中垂直纸面向外的方向上只有一个洛伦兹力，所以这种情况下小球也不能沿竖直方向运动；C图中小球所受三个力的合力如果为零，小球就可以沿竖直线运动；D图中小球只受竖直方向两个力作用，一定沿竖直线运动．答案：CD

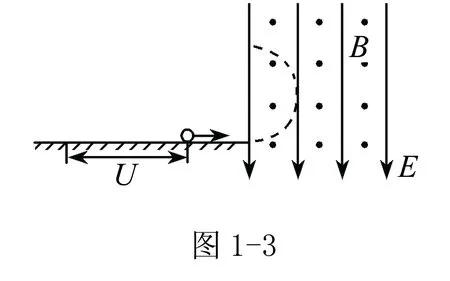
练习2 (2014年杭州高三质检)如图1-3所示，已知一带电小球在光滑绝缘的水平面上从静止开始经电压U加速后，水平进入互相垂直的匀强电场E和匀强磁场B的复合场中(E和B已知)，小球在此空间的竖直面内做匀速圆周运动，则( ).

A．小球可能带正电

D．若电压U增大，则小球做匀速圆周运动的周期增加

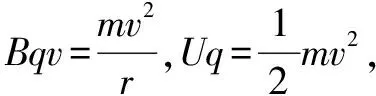
二、带电粒子在三种场重叠区域中作有约束的直线运动、圆周运动问题分析

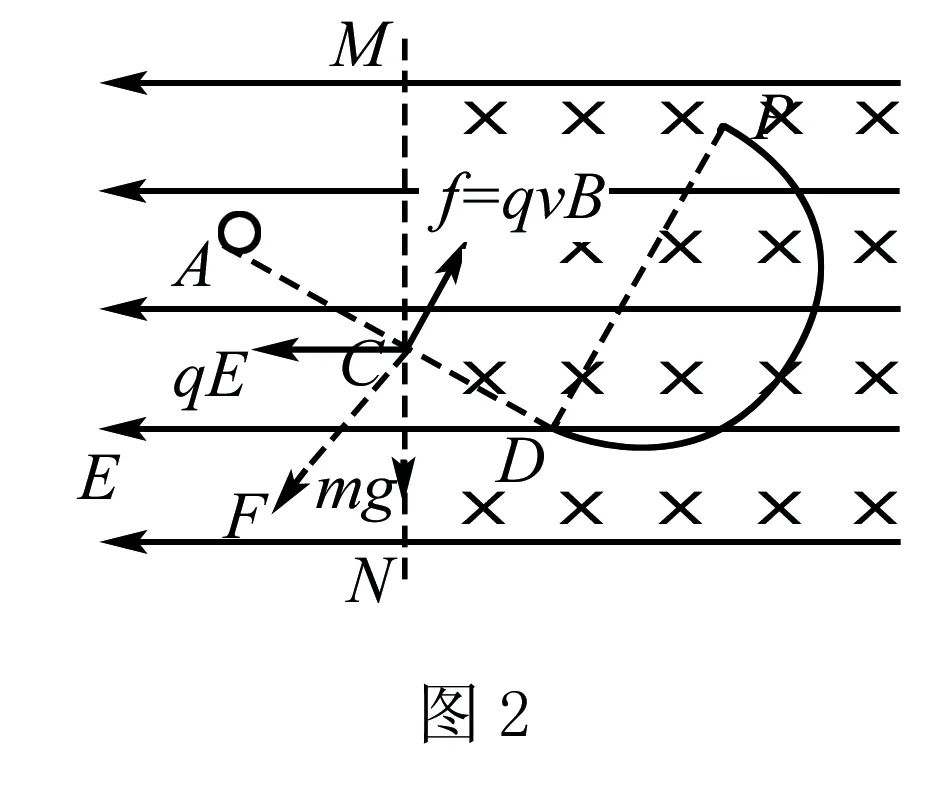
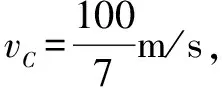
(1)小球带何种电荷？

(2)小球在半圆轨道部分克服摩擦力所做的功？

(3) 小球从P点飞出时磁场同时消失，小球离开P点后的运动轨迹与直线AC(或延长线)的交点为G点(未标出)，求G点到D点的距离？

(4) 若只将半圆轨道改成光滑且小球到达点C的速度不变、图中的原有电场与磁场均不变，则小球在半圆轨道上运动中对轨道的最大压力及最小压力各多少？

解析(1)由于小球从C向D的直线运动中是不受约束的，故小球在CD间必将作匀速直线运动，其受到重力，静电力、洛伦兹力如图2示，且三力之合力必为0，因此带电小球应带正电荷．

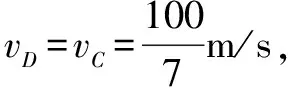
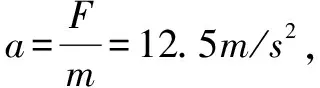
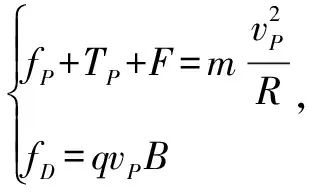
练习3 (2013年江西八校联考)如图2-1所示，在水平匀强电场和垂直纸面向里的匀强磁场中，有一竖直足够长固定绝缘杆MN，小球P套在杆上，已知P的质量为m，电荷量为+q，电场强度为E、磁感应强度为B，P与杆间的动摩擦因数为μ，重力加速度为g.小球由静止开始下滑直到稳定的过程中( ).

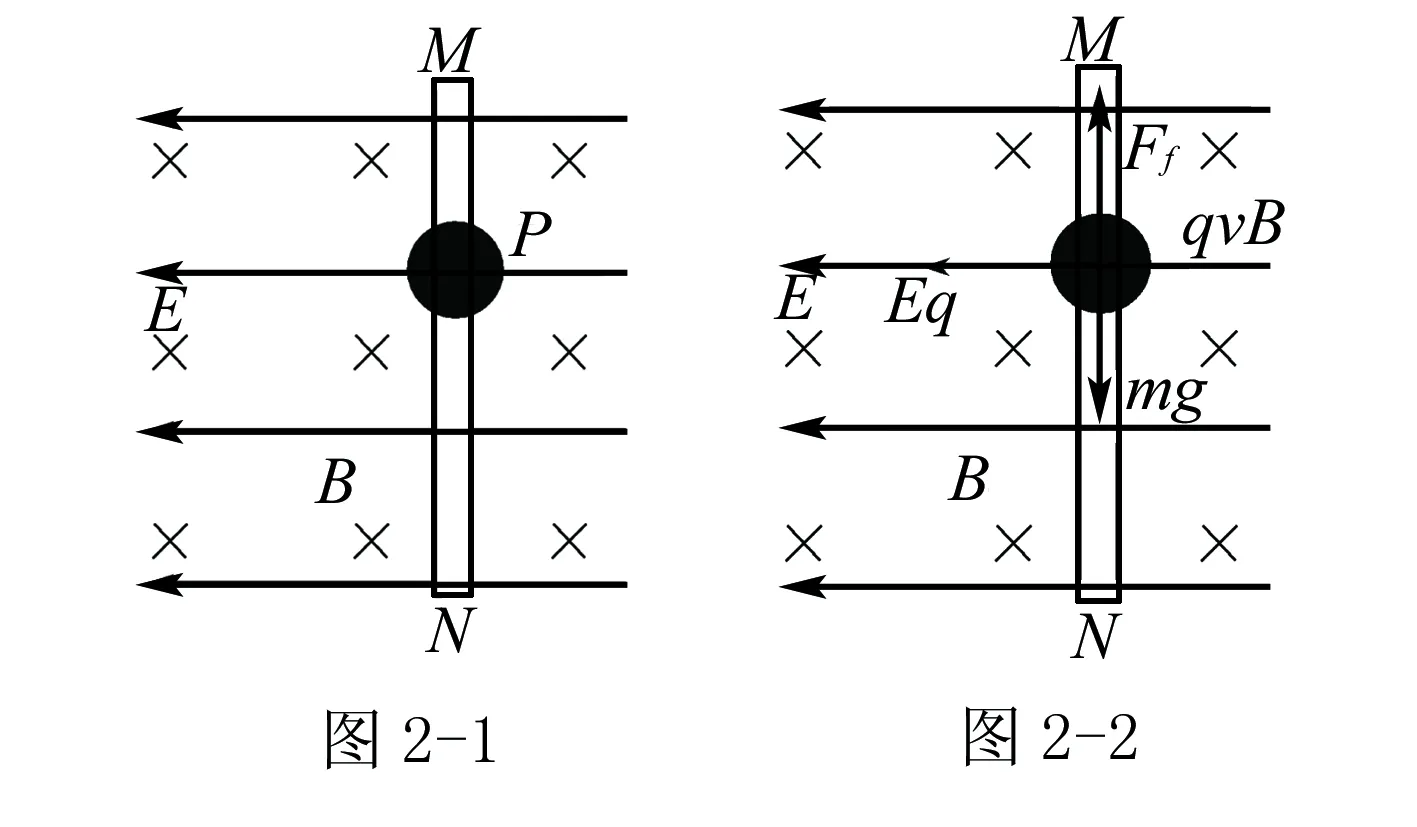
A．小球的加速度一直减小

B．小球的机械能和电势能的总和保持不变

方法总结：1.带电粒子在三种场重叠区域并受到轻杆、轨道、平面等约束情况下的直线运动——抓住洛仑兹力f=qvB随速度的变化引发的相应各力的变化，从而导致物体运动情况也会产生相应的变化；找准物理过程中力、运动的转折点(极值点、临界点)，灵活应用动力学、动能定理及能量守恒定律处理；

2.注意粒子受到的等效重力及平衡位置：

等效重力G等——将重力与电场力之合力G等来替代此二力即称G等为等效重力；

平衡位置——带电粒子或小球在约束下能保持静止时的位置；

3.带电粒子在三种场重叠区域并受到轻杆、轻绳、圆环、轨道等约束下的圆周运动：

①粒子圆周运动中的物理最高点——粒子或小球的平衡位置相对于圆心的对称点.

②粒子受轻绳、内轨道约束下绕圆心作圆周运动的临界条件——粒子经过物理最高点时受到的约束力大于或等于0即T最高点≥0；

③粒子受轻杆、圆环约束下绕圆心作圆周运动的临界条件——粒子经过物理最高点时的速度大于或等于0即v最高点≥0；

④粒子变速运动中经过平衡位置时其受到的约束力必最大；粒子或小球受轻绳、内轨道约束时其经过物理最高点时受到的约束力最小且方向必沿半径向圆心；粒子或小球受轻杆、圆环约束时其经过物理最高点时受到的约束力的大小与方向将随其经过此位置的速度大小而不同；

⑤粒子变速运动中灵活应用动力学、动能定理及能量守恒定律处理；

⑥粒子作匀速圆周运动的条件——粒子受到的电场力与重力(或此二力在其圆周平面上的分力)必等大、反向、共线即此二力平衡，粒子只在洛仑兹力作用下作匀速圆周运动，即洛仑兹力作向心力；

三、带电粒子在重叠场区域中作一般曲线运动的分析

例3 (2013年高考福建理综)如图3甲，空间存在一范围足够大的垂直于xOy平面向外的匀强磁场，磁感应强度大小为B.让质量为m，电荷量为q(q>0)的粒子从坐标原点O沿xOy平面以不同的初速度大小和方向入射到该磁场中．不计重力和粒子间的影响．

(1)若粒子以初速度v1沿y轴正向入射，恰好能经过x轴上的A(a,0)点，求v1的大小．

(2)已知一粒子的初速度大小为v(v>v1)，为使该粒子能经过A(a,0)点，其入射角θ(粒子初速度与x轴正向的夹角)有几个？并求出对应的sinθ值．

(3)如图3乙，若在此空间再加入沿y轴正向、大小为E的匀强电场，一粒子从O点以初速度v0沿y轴正向发射．研究表明：粒子在xOy平面内做周期性运动，且在任一时刻，粒子速度的x分量vx与其所在位置的y坐标成正比，比例系数与场强大小E无关．求该粒子运动过程中的最大速度值vm.

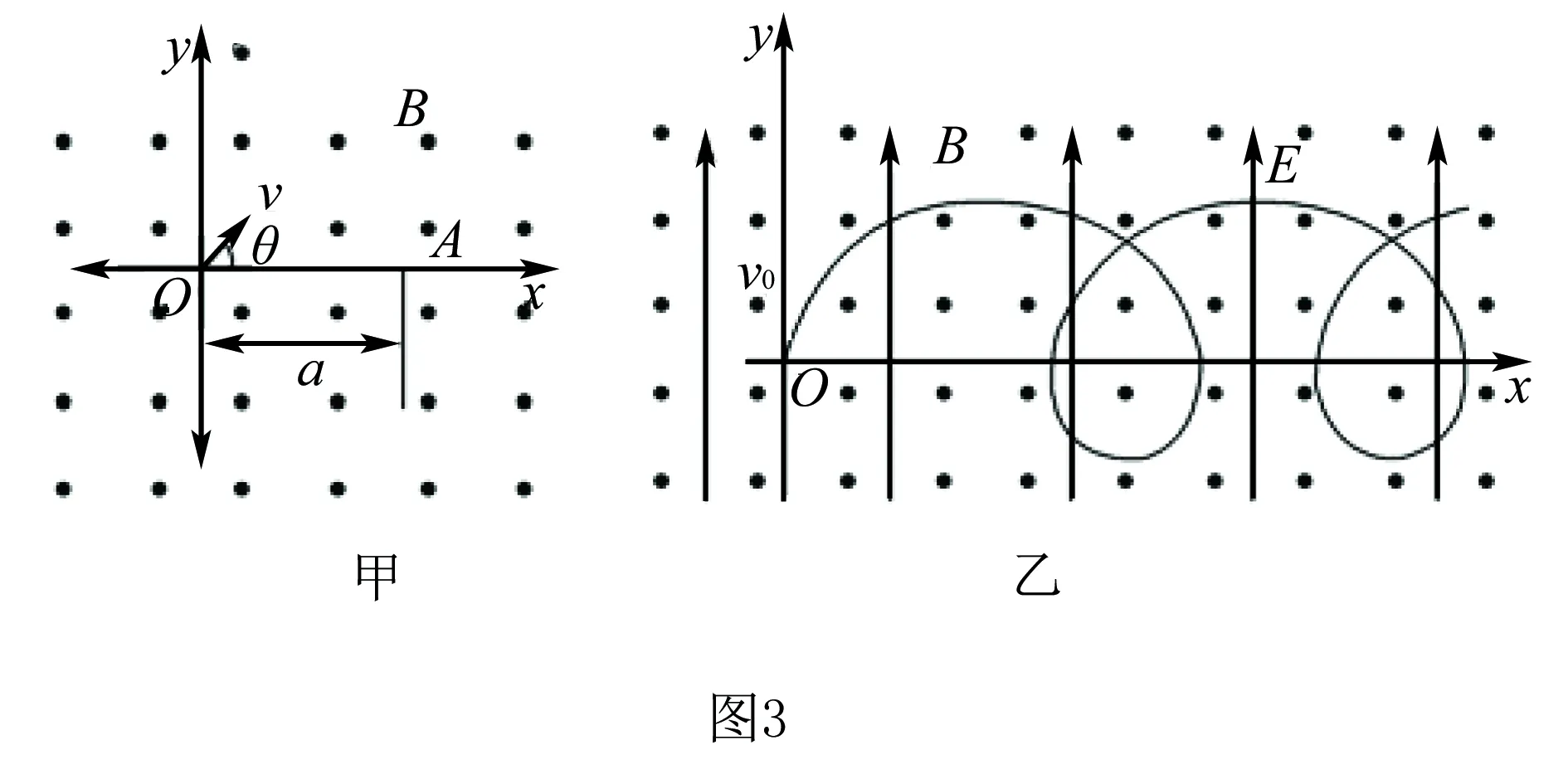
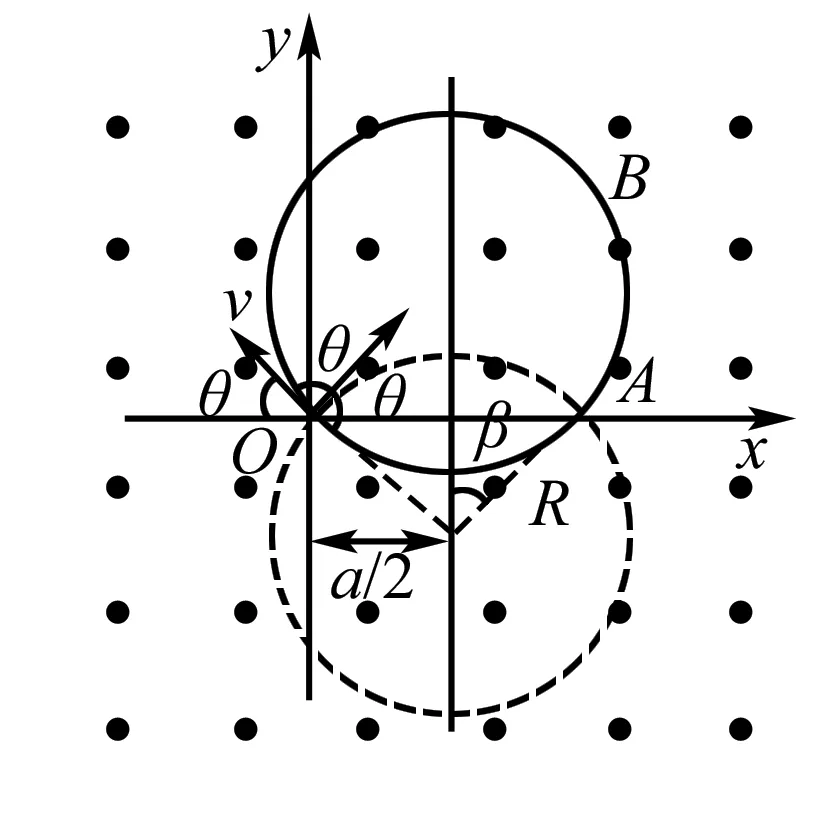
图4

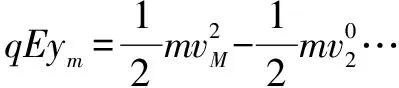
总结：粒子在一般曲线运动中其速度大小、方向均是变化的，故其受到的洛仑力f=qvB必为变力，对运动中的特殊状态可用动力学方法处理相关的运动和力的关系问题，对运动过程则要充分利用动能定理与能量守恒定律加以处理，特别注意洛仑兹力始终不做功.

参考文献：

[1]李凤环.带电粒子在电场中的直线运动[J].数理化学习(高中版),2004(12).