基于主从博弈的负荷聚合商奖励价格制定策略及可控负荷调度研究
2018-06-06蒋东荣向洪伟王一雯陈冠霖王培懿
蒋东荣,向洪伟,王一雯,贾 勇,陈冠霖,王培懿
(1.重庆理工大学 电气与电子工程学院, 重庆 400054;2.重庆市能源互联网工程技术研究中心, 重庆 400054;3.西南大学附中高2019级, 重庆 400715)
居民用电量的增长和可再生能源的大量接入给维持电力生产和消费的实时平衡带来了巨大挑战[1-2]。需求侧管理(demand-side management,DSM)通过经济刺激需求侧用电变化被认为是解决这种挑战最有效的一种方法[3]。实时电价(real-time pricing,RTP)[5-6]的提出鼓励用户根据价格调整用电安排,解决发电变化和输配电网络故障带来的供需平衡问题[7],但也会造成新的用电高峰和低谷,所以在实时电价背景下,负荷聚合商制定奖励价格对需求侧进行管理具有十分重要的意义。
国内外学者对于DSM方法已经进行了大量的研究,主要可归纳为两类。
第一类为家居负荷调度策略。周磊等[8]构建了家居负荷模型,以用户电能成本最小化与系统峰谷差最小化为目标对用户能量进行管理。曾鸣等[9]构建了用户成本最小化和负荷波动最小化的能量管理系统两阶段模型。Foster等[10]在用户提供给负荷聚合商电动汽车出行信息、负荷聚合商考虑电网安全约束的条件下,制定个人最优充电策略。于雷等[11]将家居负荷进行了具体的分类,并构建了用户经济最优和负荷平稳的多目标建模,利用混合二进制微分进化算法对不同类型负荷的运行方式进行优化。这类调控策略的不足之处在于:用户满意度模型较为简单,调度方案并非用户最优用电方案。
第二类为定价策略。魏韡等[12]基于电动汽车代理商和车主各自追逐利益最大化的主从博弈模型,建立了电动汽车充电分时定价策略。杨健维等[13]在考虑电网电压安全风险的基础上,基于电动汽车代理商和车主各自追逐利益最大化的主从博弈模型,建立了住宅区电动汽车代理商定价策略。上述定价策略的局限为:用户通过价格自行安排用电策略可能会在低电价时形成新的用电高峰,对电网安全造成危害。Sarker等[14]以用户满意度和电网安全为基础,负荷聚合商通过制定经济激励方案形成家居负荷最优协调与调度,但未对经济激励进行具体研究。
基于此,本文分析实时电价引导下的家居负荷波动对电网安全的影响,研究基于现货市场购电风险、电网安全风险和缺供电风险的负荷聚合商定价策略,运用主从博弈理论确定奖励价格引导下的家居负荷调度模型。最后,以IEEE 4节点配电系统为仿真算例,定量分析了定价策略对系统安全和聚合商收益的影响。
1 负荷聚合商运营模型
负荷聚合商不仅是负荷调度公司,也可以是一个能对负荷进行管理的售电公司,他们可以拥有自己的配电网络。如果聚合商需要使用其他配电网络,那么他将支付配电网络使用成本[4],使用成本包含负荷波动对电网造成的风险成本。为使聚合商购电成本最小和配电网使用成本最小,本文建立了聚合商在日前与用户进行两阶段互动模型,具体步骤如下:
1) 负荷聚合商在第1阶段根据发电厂日前发电预测和日负荷曲线,考虑用户响应价格弹性,形成次日各个时段电价信息。各时段电价可由购电成本、配电网使用成本和负荷聚合商利润构成。
2) 用户在第1阶段,根据电价信息,在满足自身舒适度的前提下来安排各种用电设备次日用电时段以及需求电量,使用电成本最小化,并将用电信息传回负荷聚合商。
3) 负荷聚合商在第2阶段,依据用户用电信息,以收益期望最大化和风险最小化为目标,制定各个时段的奖励价格并对响应负荷进行调度。
4) 用户在第2阶段,根据奖励价格和自身满意度,按照用电成本最小化安排设备进行响应。
2 风险指标
2.1 购电风险
负荷聚合商在合约市场和现货市场向发电公司购电。由于合约电价是事先商定的,为已知量,所以负荷聚合商的购电风险主要表现为现货电价的不确定性[16]。但在一个运行平稳的电力市场中,现货电价是负荷的随机变量。根据对美国PJM(Pennsylvania-New Jersey-Maryland)日前市场的电价结果可知,PJM日前市场电价的均值、标准差与其对应的负荷呈线性关系,即
(1)
式中:μ(px(L(t)))、σ(px(L(t)))分别为L(t)负荷水平下现货市场的电价均值和标准差;μ0和α、σ0和β分别为现货市场电价均值和标准差直线的拟合参数。
2.2 电网安全风险
电网安全风险主要是潮流越限和电压越限对系统安全的影响[17],并且其越限程度越高风险越大,其安全风险指标为
(2)
式中:IRGS为电网安全风险指标;SLoadl为第l条线路潮流越限严重度;SVoltagen为第n节点电压越限严重度;krisk为严重度经济折算系数。
2.3 缺供电风险
缺供电风险主要是大规模停电会对社会生产造成影响,负荷聚合商需要承担一定的责任。缺供电时间、缺供电量和负荷区的重要度是影响缺供电风险大小的主要因素,即
(3)
式中:IRSI为电网缺供电风险指标;qsi为第i个负荷区的缺电量;tsi为第i个负荷区的断电时间;ks为缺电事故的社会影响系数;kP为负荷区的重要度;CP为缺电事故负荷聚合商受到的处罚金额。
3 考虑风险指标的负荷聚合商奖励价格制定模型
3.1 负荷聚合商奖励价格制定原则
为了保证配电网络潮流安全运行,并考虑到每个用户有独特的用电习惯,用户对奖励价格的响应与用户收入、控制用电负荷的能力等因素有关,负荷聚合商必须制定出基于时间并含不同等级的奖励价格πt,i,刺激用户调整用电,其中t表示第几个时间尺度,例如将时间尺度设为15 min,则一天将有96个时间尺度,i表示奖励价格等级。不同奖励价格等级πi与用户响应量的关系[15]如图1所示。
负荷聚合商只需对需要进行负荷削减的时段制定奖励价格。只要用户在存在奖励价格的时间尺度内参与响应都能获得奖励价格。聚合商制定奖励价格必须以收益最大化为原则,即奖励价格因与削减多少负荷量对应。

图1 奖励价格曲线
3.2 负荷聚合商定价策略
1) 负荷聚合商收益函数为
(4)
式中:pt、pc、px(L(t))分别为售电电价、合约市场购电电价、现货市场购电电价;ω为合约市场购电比例;L(t)为t时刻负荷;IR为由风险指标加权构成的风险成本;R为用户参与第2阶段响应奖励成本。
2) 负荷聚合商奖励成本为
(5)
式中:πt为t时刻奖励价格;Δpt为可转移负荷造成的电价转移差异;bi为第i类用电设备功率;ti为第i类用电设备恢复原来用电状态所需时间;ΔL(t)为t时刻负荷调整量。
3) 负荷聚合商目标函数
由于现货市场购电电价px(L(t))为随机变量,所以负荷聚合商收益也为随机变量。根据概率论函数,可得负荷聚合商收益均值和标准差为:

(6)
(7)
由概率论可知,标准差是对期望收益波动程度的度量,标准差越大,波动程度也越大,所以负荷聚合商定价策略目标函数为
maxμ(C)-σ(C)
(8)
4) 用户目标函数
由于参与第二阶段响应的用电设备使用均在用户满意度范围之内,所以不需考虑设备调度对用户满意度的影响。用户用电策略的目标函数为用电成本最小化:
(9)
3.3 定价策略约束条件
1) 奖励价格约束
充电动态电价上下限约束:
(10)
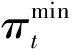
2) 可转移负荷约束
∀i∈I
(11)
(12)

(13)
式中:δt,i为i设备t时刻运行状态,当δt,i=1时表示设备i在t时刻启动,反之停机,CTi为设备i运行周期。式(11)(12)表示可转移负荷在运行周期内不可中断特性;式(13)表示i设备工作周期内所有时间段都参与响应,该设备才能参与响应。
3) 可中断负荷约束
(14)
f=f0+Δf
(15)
式中:θt是内部的温度;r为等效热阻(取0.120 8 ℃/W);c为等效热容(取3 599.3 J/℃);θout为外部温度;f0为空调初始频率(取20 Hz);Δf为频率调整值;Δt为时间间隔(min)。
短时间改变空调运行情况不会影响用户感受[18],本文假设空调在第二阶段响应并中断最长时间为15 min,响应休止时间为15 min,响应功率取该设备第1阶段在其响应时间段内的平均功率。频率调整值Δf与内部温度和用户设置温度有关,其取值可由文献[19]所得。
3.4 负荷聚合商定价模型求解
粒子群算法(particle swarm optimization,PSO)具有容易实现、计算效率高、解空间大等优点。然而,其在处理等式约束时则需引入罚函数,影响寻优效果。本文采用遗传算法与粒子群算法相结合进行求解。负荷聚合商奖励价格制定策略求解流程如图2所示。

图2 负荷聚合商奖励价格制定策略求解流程
具体步骤如下:
1) 初始化粒子群。随机产生满足奖励价格约束条件式(10)的顶层迭代粒子,设定最大迭代次数L;
2) 以式(9)为目标函数进行底层优化,得到满足家居设备约束和用户满意度约束的可控负荷。
3) 将可控负荷作为调度变量,以式(8)为目标函数进行上层遗传算法优化调度。
4) 若此时可控负荷调度迭代次数已经达到M,则令迭代次数l=l+1;否则返回步骤3)。若迭代次数l小于最大迭代次数L,则返回步骤2);否则顶层迭代全局最优解πt即为最优奖励价格,求解结束。
4 算例分析
4.1 模型参数
算例选取西南地区某小区20户居民为研究对象,分别将10用户连接在IEEE4节点配电网络最后两节点上,如图3所示。将配电网络潮流功率上限减小并且只考虑单相网络,本文假设线路有功功率上限为100 kW。

图3 IEEE4节点接线图
该用户群不同类型用电器参数如表1所示。假设每位用户都拥有表1中的用电设备[20],设每日出行前,电动汽车电池均被充满。通过天气网得到户外温度数据,奖励价格分别取[0.1 0.15 0.2 0.25 0.3]元/(kW·h),用户参与响应价格参照文献[15]进行选取。日前负荷聚合商实时电价数据如图4所示,假设本文缺电量都能从现货市场购买。通过算例验证上述所提模型的有效性。
4.2 两阶段模型优化结果
为分析用户不同用电方式对负荷聚合商的影响,分别对用户自优化和本文两阶段优化进行分析。自优化是指本文两阶段优化中的第一阶段优化。电动汽车“早出晚归型”占75%,“夜班型”占25%,负荷聚合商与用户成本如表2所示,负荷曲线如图5、6所示。

表1 用户用电器参数

图4 实时电价数据

自优化/元两阶段优化/元购电风险期望98.5473.33购电风险标准差4.082.25电网安全风险2000用户响应费用088.26负荷聚合商利润202.74312.11用户成本559.30457.76

图5 不同优化下负荷曲线
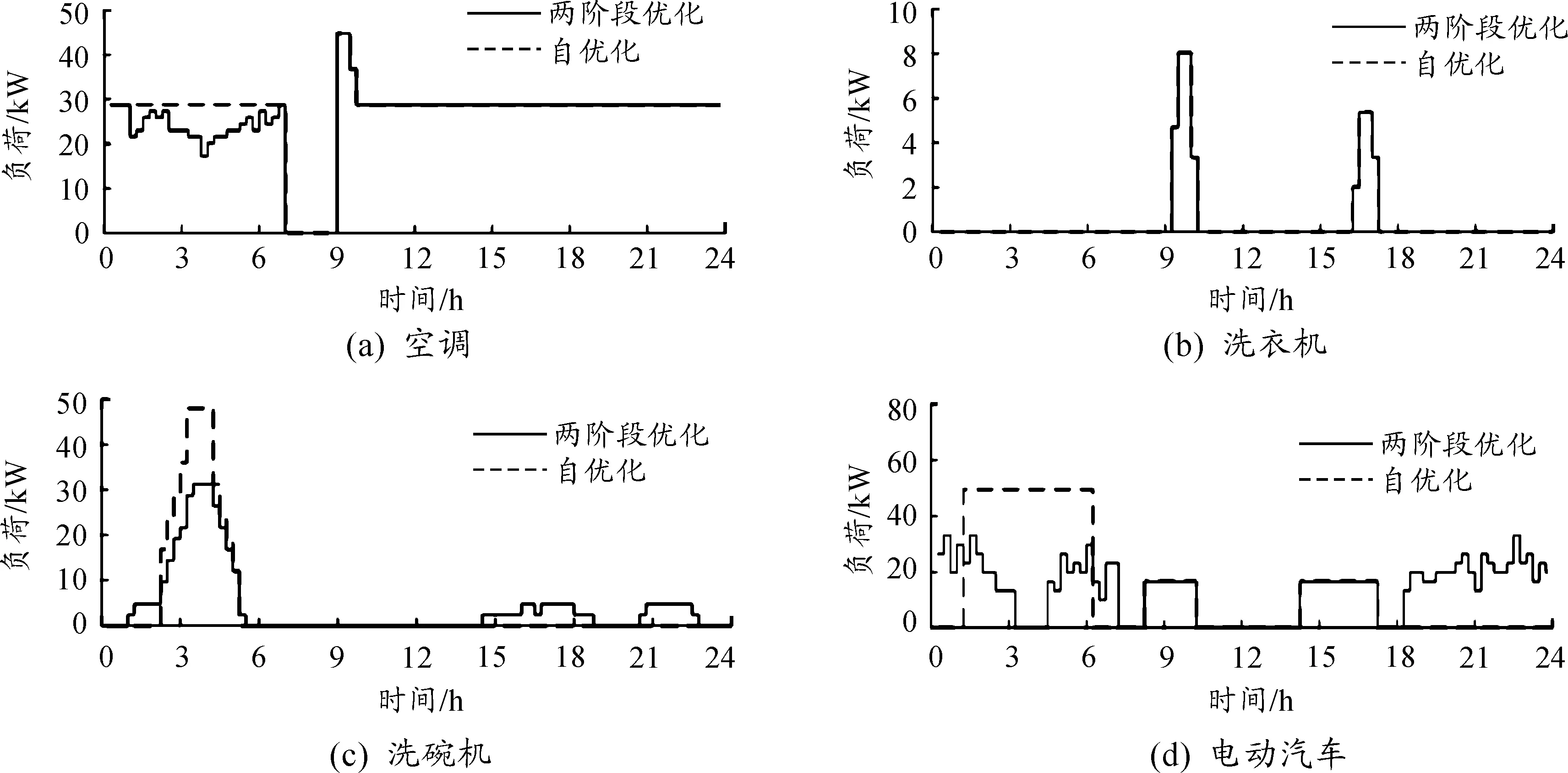
图6 不同优化下家庭设备负荷曲线
由表2可见,两阶段优化模型下的风险成本均要小于自优化模型,这是由于两阶段模型通过对再次响应用户用电设备的调度,使风险成本最小化。用户两阶段模型成本小于自优化成本,一是因为第2阶段优化模型中存在可中断负荷的响应,造成在满足用户舒适度的条件下,可中断负荷用电量的减少;二是因为用户参与第2阶段响应得到响应奖励。
由图5、6可见:在自优化模式下,由于在0∶00—7∶00时段电价较低,用户将洗碗机和电动汽车充电等大量负荷集中于该时段使用,造成负荷急剧增加达到148.9 kW,导致负荷聚合商风险成本较高。两阶段优化模型为负荷聚合商收益最大化将部分0∶00—7∶00时段洗碗机和电动汽车充电负荷转移到14∶00—24∶00时段内各用户允许的时间段进行,使得负荷曲线峰谷差变小,最高负荷为100 kW。
由表3可见,奖励价格仅在0∶00—6∶00时段存在,是由于在分时电价条件下,该时段电价最低导致电动汽车充电和洗碗机等大功率家居设备都在该时段使用,造成风险成本变大。聚合商在3∶15— 4∶15时段的奖励价格最高,即负荷波峰时段,因为在该时段峰谷差过大会引起购电风险成本和电力线路风险成本的增加。
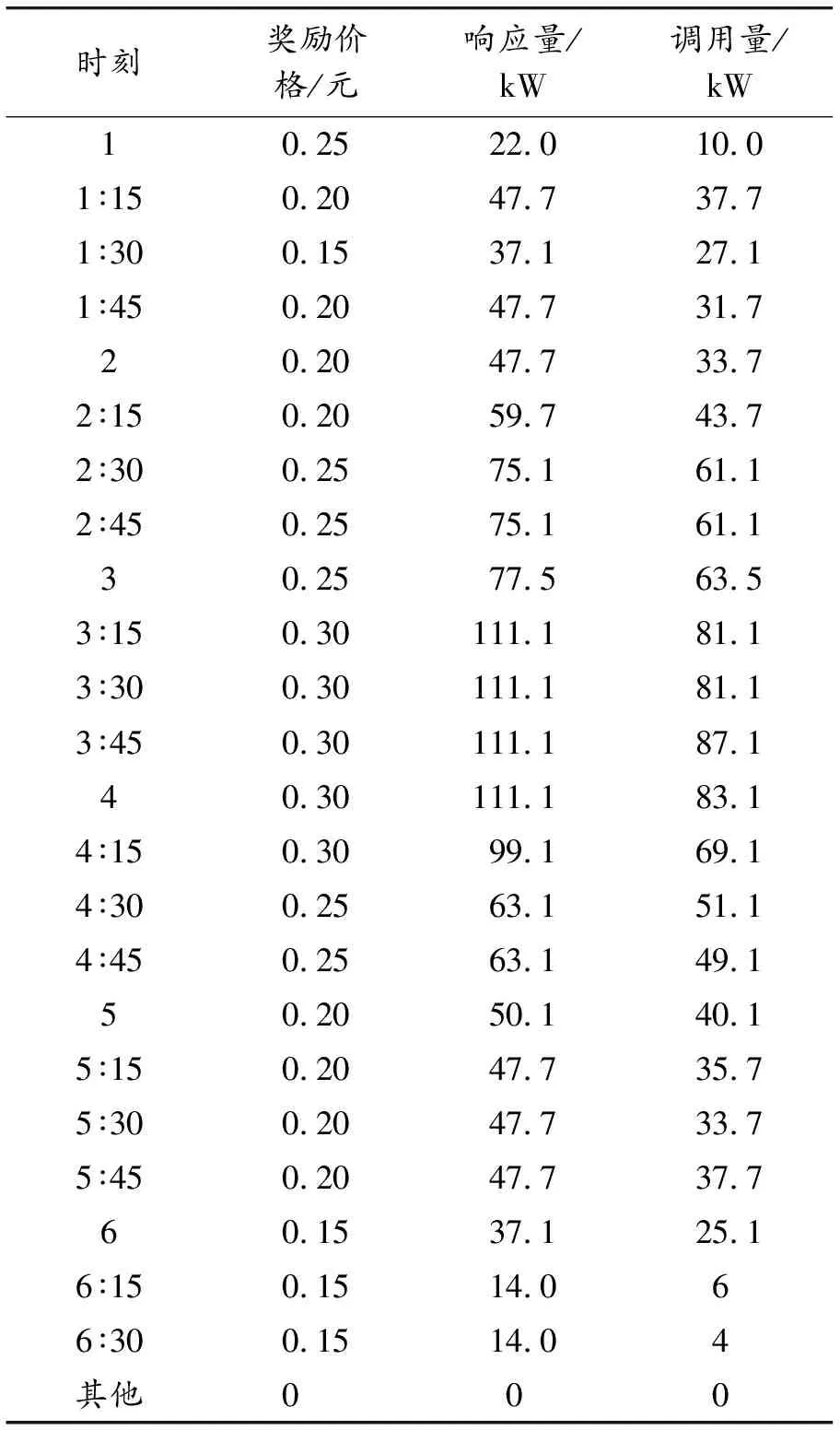
表3 负荷聚合商最优定价策略
4.3 电动汽车比例对优化结果的影响
分别改变电动汽车“早出晚归型”和“夜班型”所占比例和电动汽车数量,负荷聚合商收益变化如图7所示。

图7 不同需求和优化下负荷聚合商收益对比
由图7可以得到如下信息:① 电动汽车数量为10时,通过用户自优化,负荷聚合商收益最大,随着电动汽车数量增加到20时,仅仅依靠用户自优化,负荷聚合商的收益逐渐减少。这是因为当电动汽车数量少时,分时电价可以较好地实现削峰填谷的作用,但随着电动汽车数量的增加,将造成大量用户集中于低电价时段用电,形成新的用电高峰,导致风险成本增加。② 在电动汽车数量一定的条件下,“夜班型”和“早出晚归型”数量相等时([10,10])负荷聚合商的盈利大于“夜班型”([15,5])或“早出晚归型”([5,15])主导时,这是因为“夜班型”和“早出晚归型”数量的合理分配使自优化后风险成本最小化,所以在第二阶段负荷聚合商支出的奖励成本也会减小。③ 负荷聚合商进行两阶段模型的收益总是大于仅依靠用户自优化的收益,这是因为第二阶段目标函数为负荷聚合商收益最大化,导致奖励成本总是小于减少的风险成本。
5 结论
本文通过引入购电风险、电网安全风险、缺供电风险指标,以负荷聚合商收益期望最大和风险最小化为目标建立奖励价格制定策略,利用粒子群算法和遗传算法相结合对其进行求解。在IEEE 4 节点配电系统中进行仿真验证,得到以下结论:
1) 提出的定价策略优化方法使用户在低电价时段用电造成新的用电高峰的问题得到显著改善,各项风险指标都得到优化;
2) 该方法能保证在实时电价背景下,电动汽车、洗碗机等用电负荷逐渐增多的情况下仍能保证系统安全运行;
3) 本文的定价策略可保证随着用电负荷的增加,聚合商的总收益稳定增长。
[1] 孙元章,吴俊,李国杰.风力发电对电力系统的影响[J].电网技术,2007,31(20):55-62.
[2] 蔡德华,陈柏熹,程乐峰,等.实施需求侧管理对提高发电系统可靠性的影响探究[J].电力系统保护与控制,2015(10):51-56.
[3] VOJDANI A.Smart integration[J].IEEE Power & Energy Magazine,2008,6(6):71-79.
[4] 高赐威,李倩玉,李慧星,等.基于负荷聚合商业务的需求响应资源整合方法与运营机制[J].电力系统自动化,2013,37(17):78-86.
[5] FOX-PENNER P.Smart power:Climate change, the smart grid,and the future of electric utilities[Z].Washington,DC,USA:Island Press,2010.
[6] 刘小聪,王蓓蓓,李扬,等.基于实时电价的大规模风电消纳机组组合和经济调度模型[J].电网技术,2014(11):2955-2963.
[7] ZHONG H,XIE L,XIA Q.Coupon incentive-based demand response:Theory and case study[J].Power Systems IEEE Transactions on,2013,28(2):1266-1276.
[8] 周磊,李扬.分时电价环境下基于家居能量管理系统的家居负荷建模与优化运行[J].电网技术,2015,39(2):367-374.
[9] 曾鸣,武赓,王昊婧,等.智能用电背景下考虑用户满意度的居民需求侧响应调控策略[J].电网技术,2016,40(10):2917-2923.
[10] FOSTER J M,CARAMANIS M C.Optimal power market participation of plug-in electric vehicles pooled by distribution feeder[J].IEEE Transactions on Power Systems,2013, 28(3):2065-2076.
[11] 于雷,汤庆峰,张建华.基于负荷资源分类建模和启发式策略的家居型微电网优化运行[J].电网技术,2015,39(8):2180-2187.
[12] 魏韡,陈玥,刘锋,等.基于主从博弈的智能小区代理商定价策略及电动汽车充电管理[J].电网技术,2015,39(4):939-945.
[13] 杨健维,黄宇,王湘,等.基于动态概率潮流的住宅区电动汽车代理商定价策略[J].中国电机工程学报,2016,36(21):5822-5830.
[14] SARKER M R,ORTEGA-VAZQUEZ M A,KIRSCHEN D S.Optimal coordination and scheduling of demand response via monetary incentives[J].IEEE Transactions on Smart Grid,2015,6(3):1341-1352.
[15] 阮文骏,王蓓蓓,李扬,等.峰谷分时电价下的用户响应行为研究[J].电网技术,2012(7):86-93.
[16] 朱兆霞,邹斌.PJM日前市场电价的统计分析[J].电力系统自动化,2006,30(23):53-57.
[17] 杨汾艳,兑潇玮,唐景星,等.计入电网损失及社会影响的500 kV终端站综合风险评估[J].电力系统自动化,2013,37(22):111-117.
[18] 张志丹,黄小庆,曹一家,等.电网友好型空调负荷的主动响应策略研究[J].中国电机工程学报,2014,34(25):4207-4218.
[19] 丁强,王小华.变频空调压缩机频率控制算法的设计与研究[J].制冷与空调(四川),2006,20(3):49-52.
[20]Natural Resources Canada’s Office of Energy Efficiency.Energy consumption of major household appliances shipped in Canada 2009 [DB/OL].(2007-12-01)[2014-06-01].http://oee.nrcan.gc.ca/Publications/statistics/cama07/pdf/cama07.pdf.
