变附着系数路面的紧急避撞控制研究
2018-06-06严明月张佳佳吴树凡张凤娇魏民祥
汪 ,严明月,张佳佳,吴树凡,张凤娇,魏民祥
(1.南京航空航天大学, 南京 210016; 2.常州工学院, 江苏 常州 213002)
自动驾驶汽车利用信息感知和控制技术来提高驾驶安全性和交通效率。近年来对自动驾驶汽车主动安全的研究越来越受到关注[1]。自动驾驶汽车研究在实际道路测试时须自动对紧急情况作出反应,主动介入接管车辆完成避撞操作[2]。因此,在不能及时操控汽车时,汽车能完全代替“人”的驾驶是降低车祸发生率、避免汽车与障碍物相撞的最好手段。但是,目前无人驾驶技术远远没有成熟,汽车仍需要“人”来驾驶,因此现阶段国内外科研人员多致力于汽车部分智能化的开发,尤其是汽车主动避撞系统成为研究热点[3]。按照避撞的模式可进行如下分类:纵向制动避撞系统[4-5],主要是对车辆进行纵向制动控制以达到避免碰撞的目的;转向换道避撞系统[6],能自动控制车辆转向或避开障碍物和车辆,避免车辆发生侧面碰撞;复合型智能避撞系统[7],是指先进行自动控制转向试图避开障碍物,如果车辆不满足实施转向的要求,系统再进行自动制动。针对主动避撞有基于智能轮胎的主动避撞策略[8]、基于附着系数和驾驶意图的纵向避撞控制策略[9]。廉宇峰[10]针对四轮独立驱动轮毂电机电动汽车,研究了车辆在制动与转向两种避撞方式下主动避撞系统的状态估计与控制策略。李霖等[11]结合驾驶员避撞行为特征和车辆动力学特性的主动避撞,引入不同的TTC,提出了符合实际的换道预警避免碰撞等[12]一系列控制策略。但这些控制策略大多没有考虑路面附着系数变化对避撞控制的影响,或即使考虑了路面附着系数对驾驶行为的影响,也没有考虑路面发生突变情况下应如何控制避撞。
针对现有主动避撞控制系统的缺陷,本文设计了一种基于路面实时识别的自适应主动避撞系统。首先基于RLS对路面进行在线识别,根据路面信息实时更新安全距离模型,依据GPS、雷达等传感器的输入信息设计自适应避撞控制策略,保证车辆在传统避撞控制策略失效的情况下依然能安全稳定地避开障碍物,从而提高车辆的安全性能。
1 路面附着系数估计
本文根据魔术轮胎[13]模型,依据轮胎的纵向力与滑移率的关系,利用递推最小二乘法对路面附着系数进行实时估计。
1.1 轮胎工作区域界定
当车辆直线行驶时,对车辆有影响的纵向力包括轮胎纵向力、重力和空气阻力,忽略空气阻力,规定车辆只做纵向上的运动,没有转向行为,根据魔术轮胎模型和沿车辆行驶方向的纵向力平衡方程做出轮胎纵向力与滑移率曲线,如图1所示。
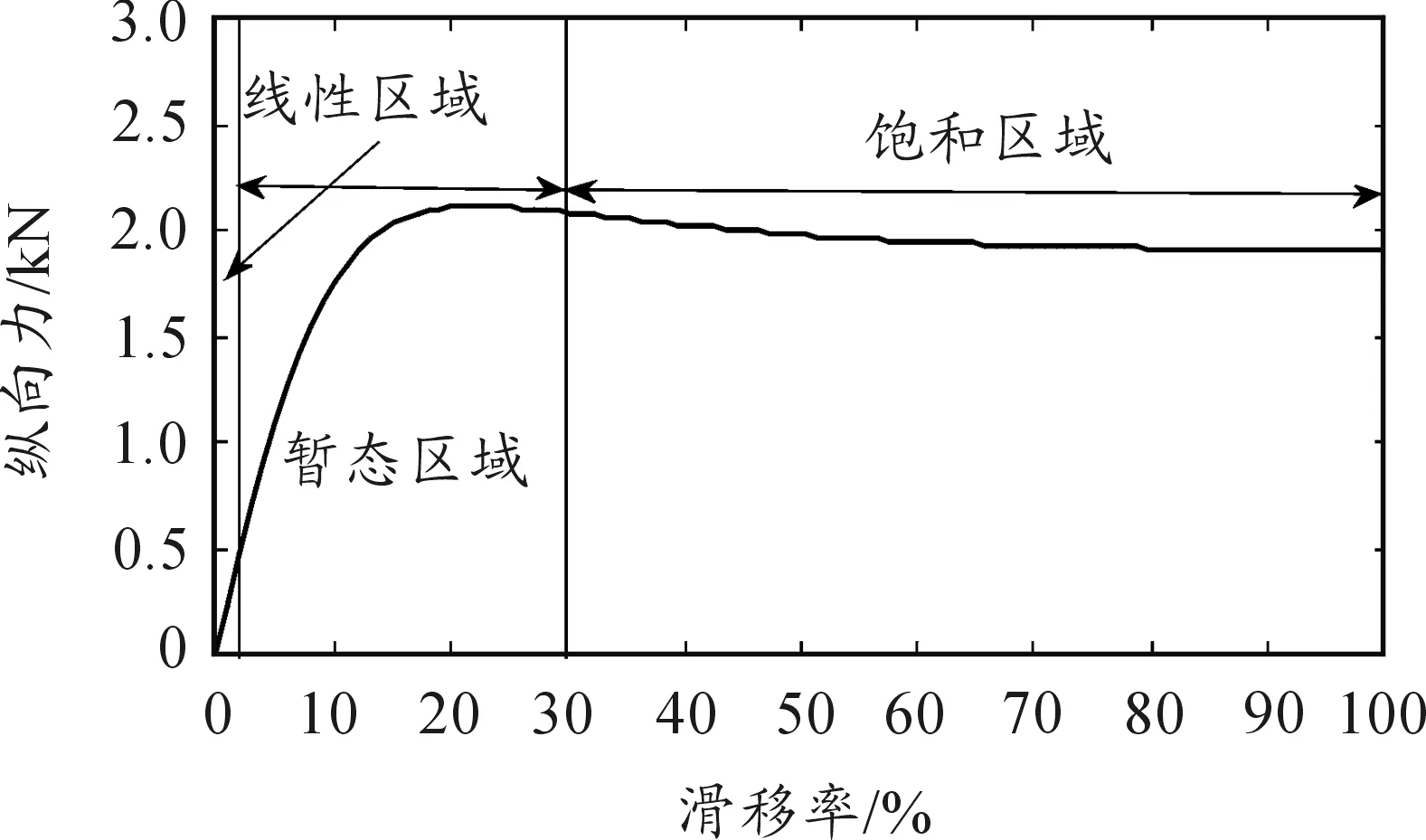
图1 轮胎工作区域
在线性区域内,轮胎纵向力与滑移率成正比,且比例系数与路面附着系数有关[14]。在饱和区域,轮胎纵向力基本不随滑移率的变化而变化,而是与路面附着系数和法向载荷有关。在暂态区域,轮胎纵向力曲线不仅受路面附着系数的影响,而且受车辆状态和路面材料的影响。在实际行车过程中,线性区域和非线性工况居多,故本文主要进行线性区域和饱和区域内的路面附着系数估计。当车辆处于暂态过程时,估计算法不更新,保存上一时刻的路面附着系数的值。
1.2 线性区域估计暂态区域
1.2.1 线性区域内路面附着系数估计过程
由于本文方法估计需要滑移率的存在,因此在车辆未发生危险工况前的正常驾驶过程中必然涉及加减速操纵,所以本文只在制动过程中进行路面附着系数的估计。仅考虑车辆的纵向运动,忽略轮胎侧向力,则
(1)

μ=Ck(μ)+D
(2)
经过大量仿真验证可得:C=0.03,D=0.07。
1.2.2 线性区域路面附着系数估计仿真分析
在路面附着系数突变的路况下,施加较小制动压力控制车辆减速,验证线性区域内路面附着系数估计方法的性能。纵向速度曲线如图2所示。车速的初始值为120 km/h,取初值θ(0)=22,协方差矩阵P(0)=1及遗忘因子ζ=0.99。
在图3的轮胎滑移率曲线中可以明显看到:滑移率曲线从高附着系数到低附着系数路面曲线出现明显下降,从低附着系数路面到高附着系数路面滑移率明显上升。在进行算法更新时取前5个时间间隔内的平均值作为输入进行均值滤波以避免估计算法失效。
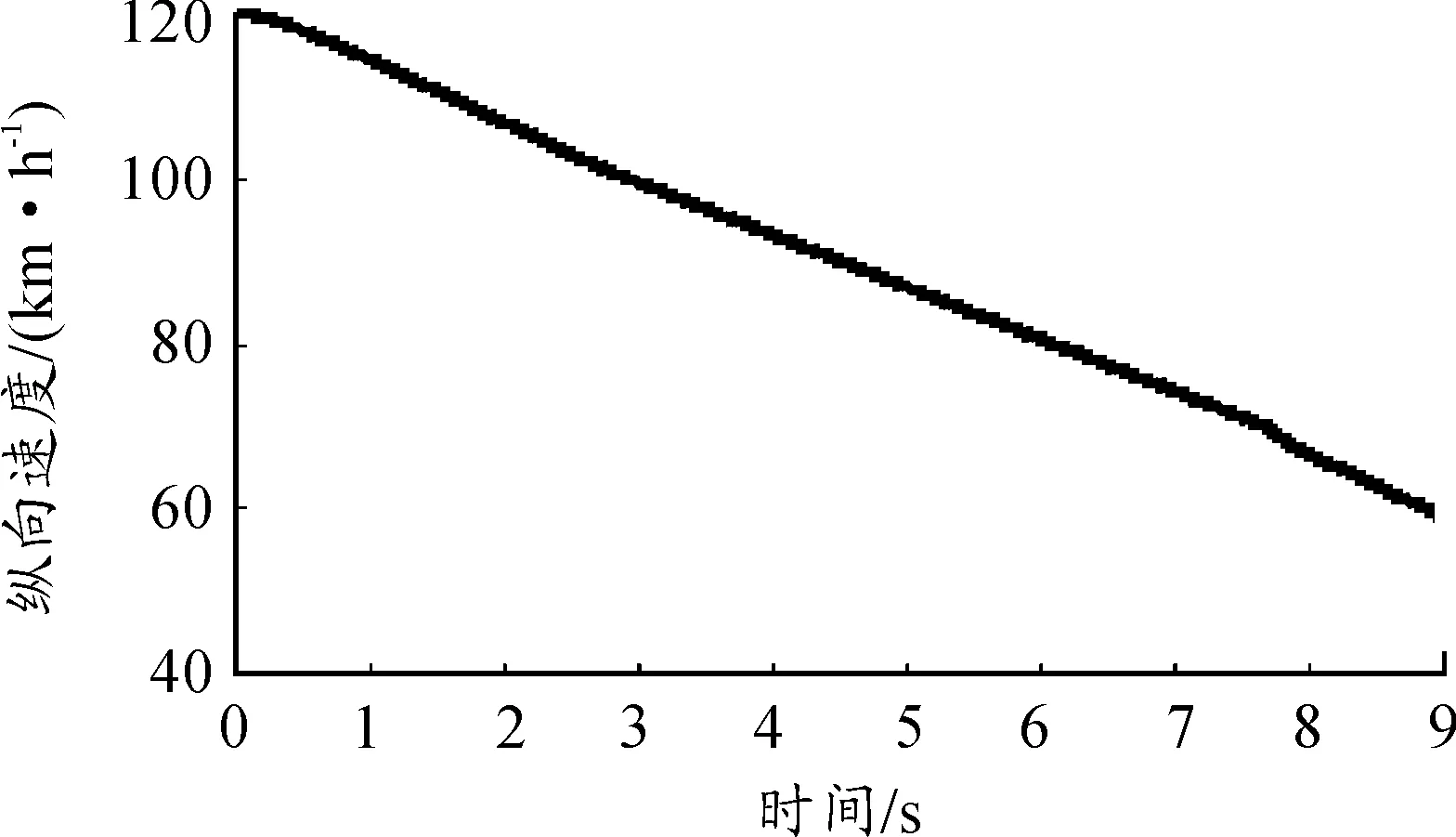
图2 纵向速度曲线

图3 轮胎滑移率曲线
路面附着系数估计曲线的仿真结果如图4所示,可见在整个过程中滑移率一直小于2%,一直处于线性范围内。由于采用线性函数映射,可以看到路面附着系数的估计曲线与滑移率曲线变化保持高度一致。估计曲线能及时跟踪路面的变化,实时性良好。在估计开始阶段,滑移率有一个下降趋势但能很快跟踪到真实值,算法的鲁棒性较好。

图4 路面附着系数估计曲线
1.3 饱和区域估计
1.3.1 饱和区域内路面附着系数估计过程
在饱和区域内即滑移率大于30%时,线性区域内的估计算法将不再适用,车轮出现滑转或抱死状态,此时纵向力达到饱和。纵向力仅与路面附着系数和法向载荷有关,如图1所示。当车轮滑移率大于30%时,轮胎纵向力出现饱和现象,由递推最小二乘法标准形式可得:y(t)=Fx是系统的输出;θ(t)=μ是系统的未知参数;φ(t)=Fz是系统的输入。
1.3.2 饱和区域路面附着系数估计仿真分析
在路面附着系数突变的路况下,施加较大制动压力控制车辆减速,验证线性区域内路面附着系数估计方法的性能。纵向速度曲线如图5所示。车速的初始值为120 km/h,取初值θ(0)=0.8,协方差矩阵P(0)=1,遗忘因子ζ=0.98。

图5 纵向速度曲线
在图6的轮胎滑移率曲线中可以明显看到:滑移率曲线从高附着系数到低附着系数路面,曲线出现明显下降;从低附着系数路面到高附着系数路面,滑移率明显上升。在刚开始阶段虽然有较大制动力,但是由于地面附着系数高,能提供较大驱动力,滑移率处于较小值。在2~7 s内由于路面附着系数突然减小,路面所能提供的最大驱动力大大减小,此时制动力远远大于驱动力,滑移率急剧增加到接近1,轮胎近乎处于抱死状态。在7 s以后轮胎的滑移率又快速恢复到较小值。在进行算法更新时,取前5个时间间隔内的平均值作为输入进行均值滤波以避免估计算法失效。
由于此部分包含线性和非线性的特性,采用单一饱和区域的动力学公式进行估计存在较大误差[15],故结合线性部分估计算法,将线性区域内路面附着系数估计方法和饱和区域内路面附着系数估计方法结合使用。当滑移率小于2%时采用前一种估计方法,当滑移率大于30%时采用后一种估计方法。路面附着系数估计的仿真结果如图7所示。由图7可见:在7 s前,估计算法能较好地跟踪实际值变化;在7 s后,估计算法相对真实值跟踪有一定的滞后,滞后时间为0.15 s左右。由于此时车辆速度不高,故存在的一定滞后对后续控制器实时控制影响很小。

图6 滑移率曲线

图7 路面附着系数估计曲线
2 纵向安全距离模型与换道路径规划
由于处于高速紧急工况,驾驶员来不及控制车辆躲避撞碍物,而是直接由控制器控制避撞,故忽略驾驶员反应时间。由文献[16]可知,纵向制动安全距离为
(3)
其中:t1为抵消制动盘和制动钳间隙所用时间;t2为制动力增加至路面附着力所用时间;μ为路面附着系数;g为重力加速度;vc为初始车速。
对式(3)分析可知:安全距离模型的影响因素有t1、t2、vc、μ。由于t1和t2时间较短,故影响安全距离模型的主要因素是vc和μ。根据式(3)做出初始车速、制动距离与路面附着系数关系的三维曲面,如图8所示。由图8可知:随着初始车速vc的增加,路面附着系数对制动距离的影响急剧增大。因此,针对车辆行驶在高速公路上的紧急避撞问题,路面附着系数的估计显得尤为重要。

图8 初始车速、制动距离与路面附着系数关系
简化的换道距离模型[17]如图9所示,其中:ye为车辆换道完成后的侧向位移,采用高速公路标准车道宽,为3.75 m;tc为预碰撞时刻;te为换道完成时间;xe(t)为车道换道的纵向位移;θ为车辆航向角。根据一元高次多项式[18]描述换道路径。
(0≤t≤te)
(4)
te取值大小会直接影响车辆在换道时的最大侧向加速度,直接关系到车辆的稳定性。仿真试验显示本文换道时间为1.5 s。
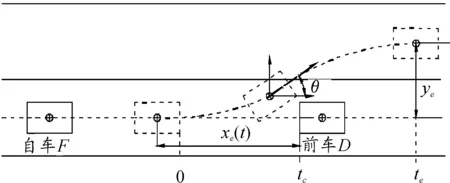
图9 汽车换道位置示意图
3 基于变附着系数路面的紧急避撞控制器设计
3.1 上层控制器设计
本文提出的自适应避撞控制策略能根据车辆行驶过程中实际路面变化进行适应不同车速、不同路面情况下的主动避撞操作,提高了避撞的适应性。车辆行驶时通过激光雷达传感器采集自车与前车的距离信息S,控制系统采用RLS算法估计所得的路面附着系数μ,根据安全距离模型得到基于当前路面条件的纵向安全距离SW。
若S=SW,自车与前车实际距离等于避撞安全距离,车辆通过制动操作进行主动避撞。避撞过程中车辆实时监测车距和路面条件,通过估计算法估计当前路面附着系数与前一时刻路面附着系数之差Δμ。考虑到同种路面估计值波动,为避免避撞方式频繁切换,取Δμ的绝对值大于0.3时为路面突变。
1) 若Δμ≥0.3,车辆避撞时路面附着条件变好,避撞距离增大,控制系统能实时判断车辆避撞方式,监测车辆安全状态。
2) 若Δμ<-0.3,车辆避撞时路面附着条件变差,此时通过制动操作难以避免与前车发生碰撞,因此系统通过转向进行主动避撞。
3) 若-0.3<Δμ<0.3,车辆路面波动不大,继续采用制动避撞操作。
若S>SW,自车与前车实际距离大于避撞安全距离,自车正常行驶,并通过雷达传感器实时检测车距和估计实际路面变化。
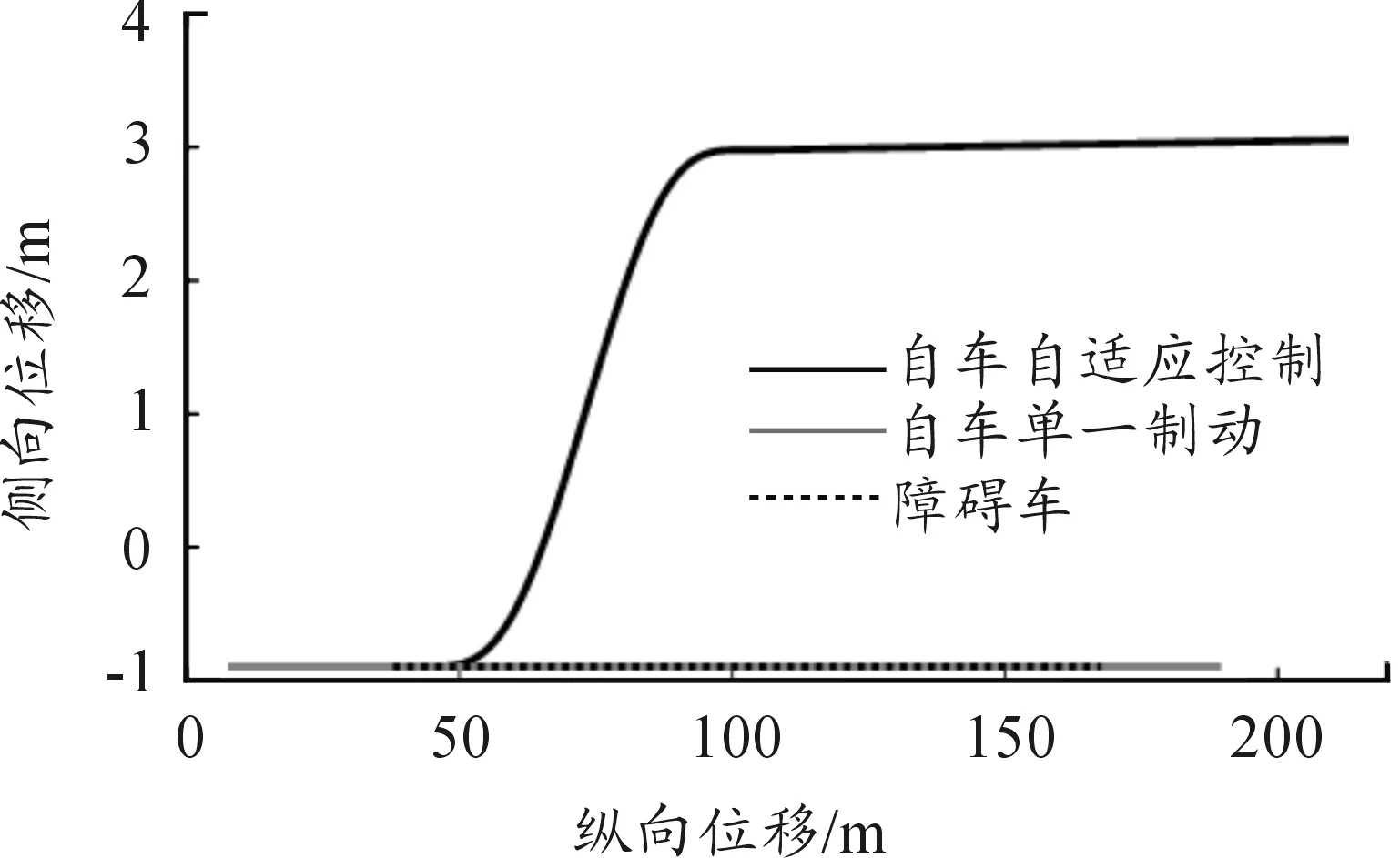
4) 若Δμ≤-0.3,S 5) 若Δμ≤-0.3,S=Sw,道路附着条件变差,两车实际距离等于制动安全距离,车辆采用制动避撞方式。 6) 若Δμ≤-0.3,S>Sw,道路附着条件变差,但实际车距仍然大于制动安全距离,车辆处于安全状态,车辆正常行驶,并实时监测车辆安全状态。 7) 若Δμ>-0.3,路面附着条件未变差,车辆处于安全状态,车辆正常行驶,通过雷达传感器实时监测车辆安全状态。 若S 8) 若Δμ≥0.3,S>Sw,路面附着条件变好,两车实际车距大于基于当前突变路面的制动安全距离,车辆处于安全状态,车辆正常行驶,并实时监测车辆安全状态。 9) 若Δμ≥0.3,S=Sw,路面附着条件变好,两车实际车距等于基于当前突变路面的制动安全距离,车辆采用制动避撞方式。 10) 若Δμ≥0.3,S 11) 若Δμ<0.3,路面附着条件未变好,车辆采用转向避撞方式。 车辆整体控制策略逻辑框图如图10所示。 图10 控制策略逻辑框图 转向下层控制器是根据转向逆动力学模型[19]求出期望的方向盘转角为理想值,方向盘转角传感器测出实际转角值,输入给控制器,在控制器内部与理想值进行比较,判断偏差的正负值,决定执行电机旋转方向。控制器输出信号控制执行机构动作,持续调节以达到理想的跟踪效果。 制动下层控制器是根据制动逆动力学模型[17]求出期望的制动压力为理想值,制动压力传感器测出实际制动主缸压力输入给PID控制器,控制器控制制动电机方向和速度使得实际压力跟踪期望压力值。转向/制动下层控制器如图11所示。 图11 转向/制动下层控制器 仿真工况设置为2类:① 安全距离以内路面附着系数突变;② 自车进入安全距离前路面发生突变,安全距离以内路面未突变。由于路面发生变化,安全距离也发生变化,此处的安全距离是基于当前未突变路面进行安全距离计算所得值,具体如图12所示。 图12 路面突变工况 在图12中深色代表低附着系数路面,浅色代表高附着系数路面。图12中的(a)和(b)表示安全距离以内路面突变,(c)和(d)表示安全距离以内路面没有发生突变,路面突变发生在进入安全距离以前的路段。三维场景模型如图13所示。 设置自车初始车速为100 km/h,障碍车初始车速为80 km/h,在仿真开始时,障碍车以最大制动减速度紧急制动。对于图12(a)的工况1,在安全距离以内路面附着系数变大,道路附着条件变好,系统实时判断两车实际车距等于制动安全距离,系统施加适应该路面的制动压力进行主动避撞,仿真结果如图14所示。传统单一制动由于不能检测路面变化,制动压力不变。自适应控制检测到路面附着系数变大有更大的地面制动力,故其停下制动距离比传统单一制动距离小,这样安全性能更高。 图13 三维场景模型 图14 工况1纵向位移时间曲线 对于图12(b)的工况2,在安全距离以内路面附着系数变小,通过制动不能有效避撞,当检测路面附着系数变小时由原制动避撞方式切换为转向避撞方式。仿真结果如图15、16所示。 图15、16中,曲线为汽车质心运动轨迹,曲线的起点代表该车的初始位置。黑色实线代表自适应控制的自车,灰色实线代表单一制动控制的自车,黑色虚线代表障碍车。初始时刻自车和障碍车相距29 m,单一制动控制的自车没有路面识别能力,在整个避撞过程中无转向操作。在图15中,时间为6 s时单一控制自车与障碍车纵向距离曲线相交且在一条直线上,两车发生相撞,单一制动避撞失效。自适应控制自车纵向距离曲线虽然也与障碍车相交,但由图16可知:此时自车已换道,自车与障碍车不在同一车道,实现了有效避撞。 图15 工况2纵向位移时间曲线 图16 工况2 纵横向位移曲线 对于图12(c)的工况3,在安全距离内路段的路面附着系数由低变高,道路附着条件变好,系统实时判断两车实际车距大于制动安全距离,车辆正常行驶,雷达系统实时监测车辆安全状态。当实际车距等于制动安全距离时,系统施加适应该路面的制动压力进行主动避撞,结果如图17所示。传统单一制动由于不能检测路面变化保持制动力不变,自适应控制检测到路面附着系数变大,有更大的地面制动力,故其制动距离比传统单一制动小,安全性能更高。 对于图12(d)的工况4,在安全距离外路段路面附着系数由高变低,路面附着条件变差,系统实时判断两车实际车距小于制动安全距离,通过制动不能有效避撞,控制系统控制车辆由制动避撞方式切换为转向避撞方式,结果如图18、19所示。 图17 工况3纵向位移时间曲线 图18 工况4纵向位移时间曲线 图19 工况4纵横向位移曲线 初始时刻自车和障碍车相距124 m,传统单一制动控制自车没有路面识别能力,避撞过程保持制动力不变。在图18中,时间为9.9 s时单一控制自车与障碍车纵向距离曲线相交且在一条直线上,表明两车发生碰撞,传统单一制动避撞失效。自适应控制时自车纵向距离曲线虽然也与障碍车相交,但由图19可知此时自车已经换道,自车与障碍车不在同一车道,实现了有效避撞。 将RLS路面估计算法与纵向安全距离结合,设计了一种适用于变附着系数路面的自适应紧急避撞控制策略。路面附着系数估计算法能实时进行路面辨识,建立适应实际路面的安全距离模型,避撞上层控制器根据实时路面附着条件变化自动决策适应不同工况的避撞方式。设计了基于PID的下层控制器,保证执行机构能实时跟随上层控制器的输出以实现有效避撞。 虚拟实验结果表明:该变附着系数路面的自适应紧急避撞控制策略可以很好地完成路面突变条件下传统单一制动控制失效情况下的紧急避撞,控制策略具有较好的自适应性。 [1] GUO J,PING H,WANG R.Nonlinear Coordinated Stee-ring and Braking Control of Vision-Based Autonomous Vehicles in Emergency Obstacle Avoidance[J].IEEE Transactions on Intelligent Transportation Systems,2016,17(11):3230-3240. [2] FUNKE J,BROWN M,ERLIEN S M,et al.Collision Avoidance and Stabilization for Autonomous Vehicles in Emergency Scenarios[J].IEEE Transactions on Control Systems Technology,2016 (99):1-13. [3] 燕来荣.避撞技术为汽车保驾护航一路畅通[J].交通与运输,2014(2):51-52. [4] 罗莉华.车辆自适应巡航系统的控制策略研究[M].上海:上海交通大学出版社,2013. [5] 侯德藻.汽车纵向主动避撞系统的研究[D].北京:清华大学,2004. [6] EIDEHALL A,POHL J,GUSTAFSSON F,et al.Toward Autonomous Collision Avoidance by Steering[J].IEEE Transactions on Intelligent Transportation Systems,2007,1(8):84-94. [7] BRANNSTROM M,COELINGH E,SJOBERG J.Threat Assessment for Avoiding Collisions with Turning Vehicles[C]//2009 IEEE Intelligent Vehicles Symposium.USA:IEEE,2009:663-668. [8] SINGH K,ARAT M,TAHERI S.Enhancement of Collision Mitigation Braking System Performance Through Real-Time Estimation of Tire-road Friction Coefficient by Means of Smart Tires[J].SAE Int.J.Passeng Cars-Electr-on Electr Syst,2012,5(2):607-624. [9] 李素华.采用dSPACE的电动汽车纵向主动避撞系统研究[J].机械设计与制造,2017(7):111-114. [10] 廉宇峰.电动汽车主动避撞系统状态估计与控制策略研究[D].长春:吉林大学,2015. [11] 李霖,朱西产,陈海林.驾驶员制动和转向避撞极限[J].同济大学学报(自然科学版),2016,44(11):1743-1748. [12] 葛如海,储亚婷,谢永东,等.基于Prescan的换道预警规则研究[J].重庆交通大学学报(自然科学版),2016,35(1):172-176. [13] PACEJKA H B.Tyre and vehicle dynamics[M].4th ed.Beijing:Tsinghua University Press,2009. [14] 李宇.基于路面辨识的行车安全距离控制研究[D].西安:长安大学,2006. [15] Gridsada P.State,Parameter,and Unknown Input Estimation Problems in Active Automotive Safety Applications[D].Minnesota:The faculty of the graduate school of the university of Minnesota,2011. [16] 余志生.汽车理论[M].北京:机械工业出版社,2014. [17] 黄丽琼.基于制动/转向的汽车主动避撞控制系统研究[D].南京:南京航空航天大学,2016. [18] WINSTON N.Continuous-curvature paths for autonomous vehicles[C]//Proc.IEEE Int.Conf.Robot.Autom.USA:IEEE,1989:1260-1264. [19] PACEJKA H B.Tyre and Vehicle Dynamics[M].2nd ed.New York:Elsevier,2006:101-117.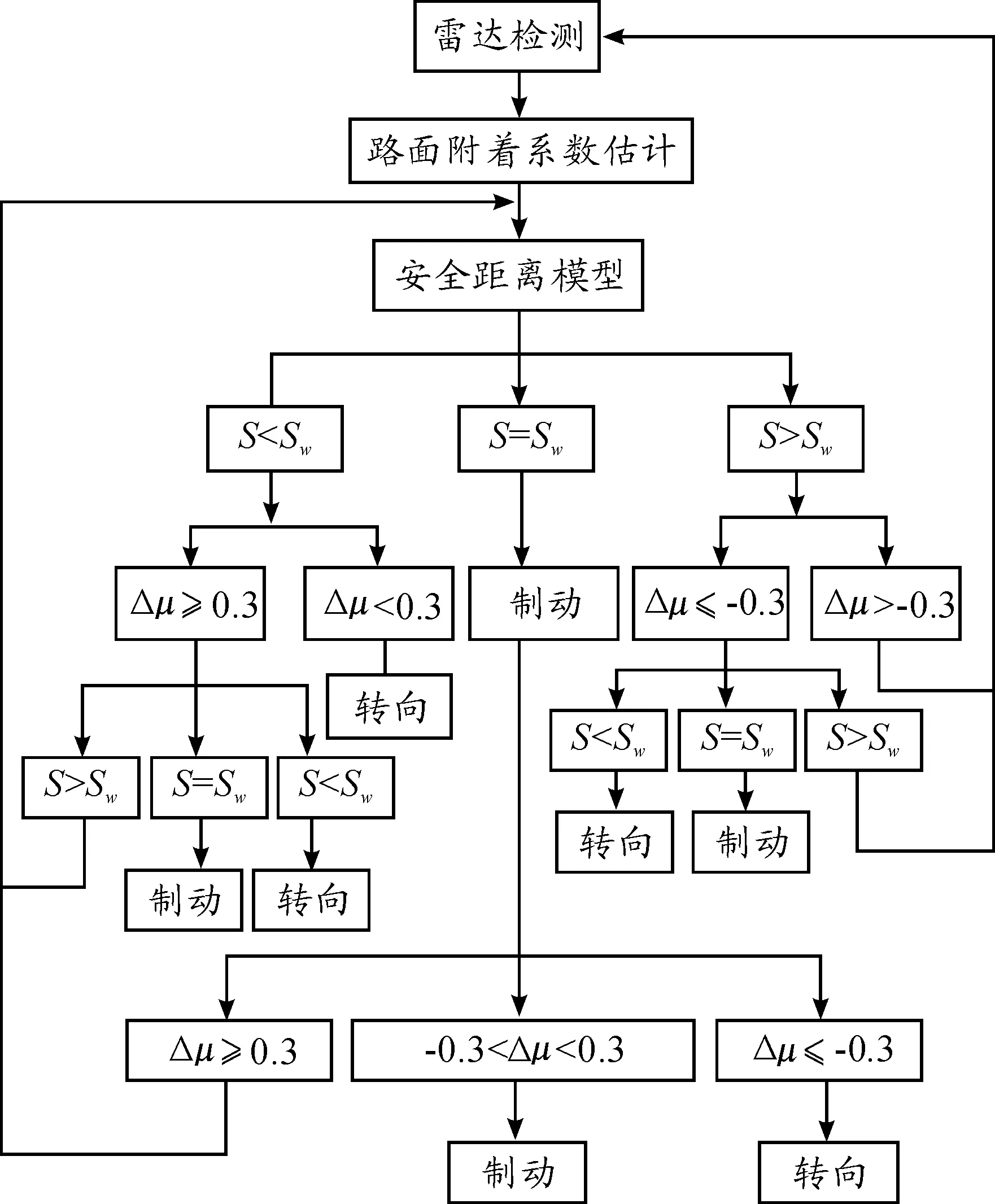
3.2 下层控制器设计

4 基于虚拟实验的算法验证







5 结束语
