基于气象因子的随机森林算法在湘中丘陵区林火预测中的应用
2018-06-06郁培义
潘 登,郁培义,吴 强
(1.国家林业局 中南林业调查规划设计院,湖南 长沙 410014;2.中南林业科技大学,湖南 长沙 410004;3.河南农业大学,河南 郑州 450002)
随着全球范围内极端天气状况频发,森林火灾的发生频次也随之增大,给国家生态环境和社会经济造成了极大损失,直接威胁现代林业的可持续发展和国土安全。据统计,全世界每年发生森林火灾22万次,受灾面积达1 000万hm2,仅欧洲,年均林火发生高达8.1万次[1],1988-2006年,我国平均每年发生森林火灾7 537次,受灾面积9.7万hm2[2-3]。由于林火广泛的影响力[4],可对森林生态系统模式和进程产生长期的扰动,包括植被分布、林分结构、碳氮循环和区域气候[5]。气候是影响森林火灾动态变化的重要因子之一,随着温度的升高,火活动将增加,火险期延长,野火发生概率升高[6-7]。因此,正确认识林火动态对气象因子变化的响应,并对二者关系进行实证分析,是开展科学林火管理的基础。湖南自然条件优越,也是我国林业发达地区之一,人工林占有较高比重,山区有经营林业的习惯,但由于自然灾害多发,火灾的频度和强度较大,加之山区地形复杂多变,过火地区受灾往往严重[8]。近年来,已有部分学者研究了该区域的林火预测模型[9-11]。
随机森林(random forest,RM)是算法模型中的一种,通过机器学习进行数据挖掘,属于一种组合式的自学习技术[12-14]。由于气象因子与林火发生的关系复杂且非线性,并且林火的发生也往往处于离散分布,加之气象因子在测量过程中可能因仪器故障或人为原因或出现缺失值,导致使用传统方法进行分析时不足以揭示复杂过程中的格局和关系[15]。分类和回归树适用于分析处于复杂关系下的生态数据,随机森林算法作为基准模型,能完成隐含特征的选择,并提供特征重要度的选择指标,往往用来做分类、聚类、回归和生存分析[16],几乎不需要测算就能够处理二分特征、分类特征、数值指标的数据,由于算法对指定使用的超参数(hyper-parameters)并不十分敏感,只需要使用大量的数,模型就不会产生很多偏差,在异常值和噪声方面有很高的容忍度,在计算时2个随机性的引入算法,也使得随机森林不易陷入过度拟合[17],当其应用于气象等生态因子的预测时,能克服协变量之间复杂的交互作用,具有较高的分类正确率[18-19]。近年来,有部分研究证明该算法在回归方面可提高林火预测精度[12,20],但国内尚未见到相关报道。本研究基于林火历史和气象因子,应用R软件,实现对湘中丘陵区林火发生的预测,将随机森林算法的预测结果与二项逻辑斯蒂回归模型的预测结果进行对比,比较不同拟合样本组合在随机森林算法中的预测精度及其在湘中丘陵区林火预测预报中的适宜性。
1 研究区概况
研究区属湖南醴陵市西南部水口山林场范围,113°19′37″-113°31′17″E,27°26′23″-27°34′55″N,系武功山系的一条支脉,低山地貌,海拔205~867m,一般坡度30°~40°,最大坡度达45°。林场内成土母质以板页岩为主,同时有少量的石灰岩、花岗岩和砂砾岩分布,风化发育的土壤以山地黄壤和山地红壤为主,亦有少量的黄壤性粗骨土分布。林场地处中亚热带季风湿润气候区,年平均气温17.8℃,年平均降水量1 500 mm,无霜期292 d。场内物种繁多,主要树种有银杏(Ginkgobiloba)、水杉(Metasequoiaglyptostroboides)、罗汉松(Podocarpusmacrophyllus)、马尾松(Pinusmassoniana)、樟(Cinnamomumcamphora)、杉木(Cunninghamialanceolata)等。林分类型以马尾松林、杉木林、针阔混交林和阔叶混交林为主。
2 数据来源与处理
2.1 数据来源
林火数据来源于醴陵市森林防火办公室1988-2014年水口山地区林火发生情况数据,水口山地区共发生火灾205次,其中,水口山林场内产生火点192次,其余地区产生火点13次;主要原因为上坟祭祀、燃放鞭炮、烧垃圾、小孩玩火和电线短路,统计火灾类型均为森林火灾。
气象数据来源于醴陵市水口山林场气象观测点1988-2014年日气象数据,包含降水量、风速等20个气象因子,初步筛选、剔除因设备原因而缺失值过多的因子(气压值、太阳总辐射、散射、直接辐射、反射辐射、净全辐射量),选定9个因子进入模型进行拟合:日均气温(0.1℃)、日最高气温(0.1℃)、日最低气温(0.1℃)、日照时数(0.1 h)、日均相对湿度(%)、日最小相对湿度(%)、日最大风速(m·s-1)、日均风速、20:00-20:00时降水量(mm)。此外,通过对林分内可燃物物理性质的测定,基于加拿大森林火险天气指标系统[22-24],计算3个反映可燃干湿程度的指标,即细小可燃物湿度码、腐殖质湿度码和干旱码;同时推算3个反映火行为的指标值,即初始蔓延速度、累积指数和火险天气指数。细小可燃物湿度码(fine fuel moisture content,FFMC)是指森林中干重为0.25 kg·m-2、厚度为1.2 m的枯枝落叶及细小可燃物的含水率,它是细小可燃物易燃程度的定量表征之一,其核心是水分交换指数模型,一般来说,可燃物湿度越大,引燃临界值越高,易燃性越差,FFMC受降水量、降水频率、相对湿度、日照条件和风速等影响,变化范围为0~101,其核心是简单的水分交换的指数模型,即:
mo=147.2×(101.0-CFFMC)/(59.5-CFFMC)
(1)
式中,mo为前一天的细小燃料的含水率,CFFMC为前一天的FFMC值。
腐殖质湿度码(duff moisture content,DMC)是反映半分解、半腐烂的凋落可燃物湿润程度的指标,受降水、相对湿度和温度的影响,DMC最小值为0,最大值没有上限,但很少超过150,计算公式为:
Mo=20.00+ln[(CDMC-244.74)/-43.43]
(2)
式中:Mo为前一天的地表可燃物的含水率,CDMC为前一天的DMC值。
干旱码(drought code,DC)是计算长期干旱对森林可燃物影响的指数,主要测量对象为深层下层落叶层和大型段木,最小值为0,最大值没有上限,但很少超过1 000,计算公式为:
Qo=400×e-CDC/400
(3)
式中,Qo表示前一天干旱码的湿度当量,CDC为前一天的DC值。
累积指数(build-up index,BUI)由DMC和DC计算得到,表示可燃物的湿度等级,在FWI系统里,相对代表了森林可燃物潜在消耗量(有效可燃物量);火险天气指数(fire weather index,FWI)由初始蔓延速度(initial spread index,ISI)和BUI计算得到[25],BUI和ISI的计算公式为:
BUI=(0.8×DMC×DC)/(DMC+0.4×DC)
(4)
ISI= 0.208×91.9×e-0.138.6m
(5)
式中:w为风速。一般情况下,风速每增加13 km·h-1,ISI值会增加1倍。
当BUI≤80,BUI-FWI=0.1×ISI×(0.626BUI0.809+2);当BUI>80,BUI-FWI=0.1×ISI×[1 000/(25+108.64×e-0.023×BUI)];BUI-FWI转化为FWI的公式:
FWI=2.72×(0.4354lnB-FWI)0.647
(6)
通过对FWI指数进行划分,可对火险等级进行划分,往往与FWI系统中其他指标一起协同预测火灾。
2.2 数据处理
使用LR(logistic regression model,二项逻辑斯蒂回归模型)和RF(random forest,随机森林算法)构建判别模型,根据前人研究,按照1∶2的比例选取对照点(非火点)。LR采用SPSS20.0软件进行计算,RF采用R软件实现。
3 研究方法
3.1 二项逻辑斯蒂回归模型
3.1.1 逻辑斯蒂回归模型的基本原理 通常情况下,森林火灾极少在短时间内完成点燃-燃烧-熄灭全过程,故本研究的模拟假设前提为森林可燃物被引燃后可持续保持燃烧状态直至人为行为干预。假设林火发生的概率为P,不发生林火概率为1-P,为保证时间序列平稳且方差恒定,对P进行对数变换(log transformation),标记为Logit(P),则林火发生概率(P)与进入模拟的气象因子(X)之间的回归关系可描述为:
可变换为:
(7)
式中:P为林火发生的概率;n为气象因子总数;β1,β2,…βn为各个自变量的逻辑斯蒂回归相关系数;X1,X2,…Xn为影响林火发生的自变量[26-27]。
3.1.2 逻辑斯蒂回归模型的校验 受试者工作特征曲线(receiver operating characteristic curve,ROC)又称为感受性曲线(sensitivity curve),与传统评价方法不同,ROC无需将试验结果分为两类再进行统计分析,而是依据不同判定标准,对同一信号刺激各自作出反应,以假阳性率为横坐标,真阳性率为纵坐标绘制曲线,ROC检验对阈值没有依赖,允许有中间状态。ROC曲线越靠近左上角,试验准确性越高,亦可根据ROC曲线下的面积(area under the curve,AUC)进行比较,AUC越大,试验准确性越高。在本研究中,根据AUC值判断试验效果,当AUC=0.5时,判定预测为完全随机,效果最差,在(0.5,0.7]区间,准确性较低,在(0.7,0.8]区间,准确性中等,在(0.8,0.9]区间,准确性较好,在(0.9,1]区间,预测具有高准确性。此外,根据ROC曲线可以计算约登指数(youden index),用于评价筛选试验真实性的方法,通过模型的敏感性值和特异性值,可以计算最佳临界值(cut-off point),如果林火的发生(预测)概率>临界值,则可判定为有森林火灾发生,反之,则可判定为无森林火灾发生[28-29]。
3.2 随机森林算法


(8)
式中,VI为变量重要性。
3.3 模型变量选择及运算
从总体样本中随机抽取60%的数据用于建模,余下的40%样本数据用于检验模型[19],为排除个例干扰,抽取重复5次,分别对5个不同的样本组合进行逻辑斯蒂运算,在每个样本组中筛选出各组的显著变量,当某变量在5个模型中出现次数不低于3次,则判定为最终变量,进入全样本模拟。
为了保证对比时的一致性,随机森林和逻辑斯蒂模型的每一次运算均采用同一套数据样本。模拟过程通过R软件中的varSelRF程序包实现,同样对5个样本组进行运算,确定最终的特征变量后纳入全样本中进行模拟。
4 结果与分析
运用SPSS对醴陵水口山地区林火数据及对应的气象因子数据进行基本统计(表1)。
4.1 二项逻辑斯蒂回归模型的拟合
4.1.1 多重共线性诊断 在线性回归模型中,解释变量之间若存在精确或高度相关关系,会使参数估计值的方差增大,容许度降低,使模型估测准确率降低或失真,故在检验特征变量与因变量的关系时,须先进行特征变量的多重共线性(Multicollinearity)诊断,以便将存在完全共线性或近似共线性的解释变量(自变量)剔除。容许度是方差膨胀因子的倒数(variance inflation factor,VIF),故容许度越大,VIF越小,说明共线性越强,本研究运用VIF对所有气象因子数据进行多重共线性检验,剔除了VIF>5的自变量[37],其公式为:
(9)
式中:R2为自变量Xi对其余变量作回归分析的复相关系数。经检验,剔除了日均气温、日均相对湿度、日最高气温、BUI和FWI(VIF分别为79.215、5.712、7.154、157.875、38.045),最终,选定20:00-20:00降水量、日均风速、日照时数、日最低气温、日最大风速、日最小相对湿度、FFMC、DMC、DC和ISI共10个气象因子(VIF分别为1.506、2.072、1.513、1.544、1.900、2.812、3.823、1.756、1.921、2.874)进行模型拟合。

表1 模型变量的基本描述Table 1 Basic descriptions of model variables
注:各变量的样本数均为205。
4.1.2 逻辑斯蒂模型的拟合 运用逻辑斯蒂模型对水口山地区1988-2014年的林火数据和对应的气象因子数据进行回归分析,分布对5组样本进行运算,筛选显著变量后进入全样本进行拟合,各样本显著性见表2。
全样本数据的逻辑斯蒂模型拟合曲线R2为0.201,筛选出的解释变量与区域内的林火发生有显著相关性(表3)。
4.1.3 逻辑斯蒂回归模型的检验 图1为各样本组逻辑斯蒂回归模型拟合优度的受试者工作特征曲线(ROC)图,通过各曲线的AUC值可分别计算其敏感性和特异性值,然后判断各模型中林火发生的临界点,具体参数值为表4所示。检验结果表明:所有参与拟合的样本AUC变化范围均落在(0.8,0.9],且显著性水平均<0.001,拟合效果较好,各样本组预测准确率为71.1%~76.4%,可用于森林火灾的监测。

表2 逻辑斯蒂模型中变量在各样本中的显著性Table 2 Significances of independent variables in each sample under LR model
注:Y代表显著,N代表不显著。下同。

表3 逻辑斯蒂模型参数拟合Table 3 Parameters fitting of LR model
4.2 随机森林算法的拟合
4.2.1 随机森林算法特征变量的选择 基于1988-2014年的林火数据,结合相应的气象因子,运用随机森林算法进行拟合分析(表5)。
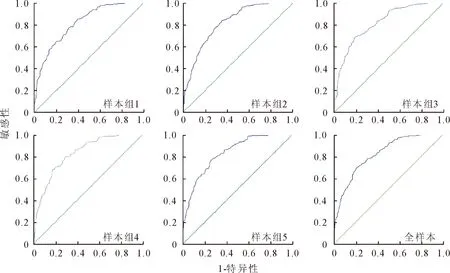
图1 模型的ROC拟合曲线Fig.1 ROC curves of logistic model

表4 逻辑斯蒂模型AUC值和临界值Table 4 AUC and threshold values of LR model
4.2.2 随机森林算法特征变量的重要性排序 利用随机森林算法对5个bootstrap训练样本组进行拟合,从各组中筛选出特征变量构成全样本组,对5个训练样本和全样本组特征变量的平均准确率降低度进行计算排序(图2)。从全样本模型的排序结果来看,日最高气温对林火发生的影响最大,其次是DC,FFMC的影响最小,从所有拟合的排序结果来看,日最高气温和DC对林火发生的影响均>其他变量。
4.2 3 种模型算法的对比分析
4.2.3.1 最终指标体系 通过分别使用二项逻辑斯蒂回归模型和随机森林算法对自变量的筛选(表6),选定最小相对湿度、FFMC和DC3个因子进入最终的模拟运算。
4.2.3.2 模型预测准确率 表7比较了二项逻辑斯蒂回归模型和随机森林算法对5个样本组的预测准确率。结果显示,随机森林算法的预测准确率要普遍高于二次逻辑斯蒂回归模型,在所有样本组的运算中,随机森林算法的预测准确率要比逻辑斯蒂模型的高7%~10%。

注:X3.日均气温;X4.日均相对湿度;X6.日最低气温;X7.日最高气温;X8.日最大风速;X9.日最小相对湿度;X10.FFMC;X12.DC;X13.ISI;X15.FWI。
图2随机森林算法对影响林火发生的自变量的重要性排序
Fig.2 Random forest affecting the occurrence of fire sort the importance of independent variables

表5 随机森林算法中变量在各样本组中的显著性Table 5 Significances of independent variables in each sample group under RF algorithm
为进一步比较2种算法的预测精度,选用全样本进行交互验证试验,即除了使用本算法的全样本数据进行模拟外,再次使用另一组全样本数据进行模拟,将拟合结果进行对比(表8)。结果表明,使用任意全样本进行模拟的随机森林算法准确率均要高于逻辑斯蒂模型的模拟结果,使用本组全样本数据进行拟合时,二项逻辑斯蒂回归模型和随机森林算法的预测准确率分别为75.3%和83.7%。

表7 逻辑斯蒂模型和随机森林算法的预测校正率Table 7 Prediction accuracy of LR model and RF algorithm

表8 指标体系交叉试验结果Table 8 Result of indicator system under crossover trial
5 结论与讨论
运用随机森林算法对湖南水口山地区林火发生与气象因子之间的关系进行了研究,并将研究结果与传统二项逻辑斯蒂回归模型的拟合结果进行了对比。结果表明,经过筛选的特征变量进入模拟时,运用随机森林算法得到的结果预测准确率始终要比二项逻辑斯蒂回归模的预测准确率高7%~10%,前者预测效果相对要好,在研究区域的适用性更高,可利用该区域的气象数据(特征变量)对当地的林火发生情况进行预测。
通过多重共线性检验,剔除了方差膨胀因子VIF>5的气象因子,筛选出显著变量组成全样本运用二项逻辑斯蒂回归模型拟合;在使用随机森林算法进行运算时,并未剔除VIF>5的气象因子,通过对各因子的重要性进行排序,发现日最高气温得分最高,对于潜在林火的发生贡献度最大,而日均气温的排序相对靠后。在对解释变量进行多重共线性诊断后,对近似共线性的解释变量直接采用了排除法,然后进行回归,当气象因子过多时,可尝试差分法将原模型变换为查分模型,或采用岭回归法(ridge regression)减小参数估计量的方差,以增加参与拟合的气象因子数量,由此可增加样本组数,进行多批次的拟合分析,从而更好地比较不同模型对于林火发生的预测准确性。
在传统的林火火险分析中,往往将森林可燃物特征作为唯一变量考虑,在非气象因子与林火发生的逻辑斯蒂模型检验中,最优模型拟合R2仅为0.15[37],说明林分特征对林火发生的解释程度并不高,需结合气象等因素进行综合分析。本研究通过多重共线性检验和随机森林的重要性排序,判定在气象因子中,日最高气温、日均气温、日最小相对湿度、FFMC和DC是影响林火发生的主要因子。相对湿度在很大程度上可影响林内活可燃物的蒸腾速率和枯死可燃物的含水率变化,对林火的发生影响较大[38-39],而气温的变化则可直接影响林内相对湿度的变化,气温的升高可加速枯死可燃物内部水分的蒸发,从而降低其着火点,此外,研究显示细小可燃物湿度码、干旱码也与林火发生具有显著相关性,这与郭福涛[40]等、Y.Chang[41]等和田晓瑞[42]等的研究结果一致。
本研究通过分析林火对气象因子的响应讨论了随机森林算法对火灾发生预测的应用效果,但在野外环境中,影响森林火灾发生的因子不仅限于可燃物特征和气象因素,还会受到人为活动、地形、(短期)历史灾害甚至区域政策等因素的影响[43-45],因此仅基于气象因子进行拟合,可能会使预测结果产生一定误差,在未来的研究中,可考虑将人为活动干扰、自然灾害、地形变化等因素纳入模型模拟范围[46-50],以进一步完善算法的准确率、精确定位模型的适宜应用范围。
参考文献:
[1] CHAS-AMIL M L,PRESTEMON J P,MCCLEAN C J,etal.Human-ignited wildfire patterns and responses to policy shifts [J].Applied Geography,2015,56:164-176.
[2] 张乃平,夏东海.自然灾害应急管理[M].北京:中国经济出版社,2009:304.
[3] ZHONG M,FAN W,LIU T,etal.Statistical analysis on current status of China forest fire safety [J].Fire Safety Journal,2003,38(3):257-269.
[4] HERAWATI H,SANTOSO H.Tropical forest susceptibility to and risk of fire under changing climate:a review of fire nature,policy and institutions in Indonesia [J].Forest Policy & Economics,2011,13(4):227-233.
[5] RANDERSON J T,FLANNER M G,JIN Y,etal.Supporting material:the impact of boreal forest fire on climate warming [J].Science,2006.314(5802):1130-1132.
[6] WESTERLING A L,HIDALGO H G,CAYAN D R,etal.Warming and earlier spring increase western U.S.forest wildfire activity [J].Science,2006,313:940-943.
[7] MARLON J R,BARTLEIN P J,GAVIN D G,etal.Long-term perspective on wildfires in the western USA[J].Proceedings of the National Academy of Sciences of the United States of America,2012,109(9):3203-3204.
[8] 苏立娟,何友均,陈绍志.1950—2010年中国森林火灾时空特征及风险分析[J].林业科学,2015,51(1):88-96.
SU L J,HE Y J,CHEN S Z.Temporal and spatial characteristics and risk analysis of forest fires in China from 1950 to 2010 [J].Scientia Silvae Sinicae,2015,51(1):88-96.(in Chinese)
[9] 王明玉,舒立福,王秋华,等.中国南方冰雪灾害对森林火灾火发生短期影响分析——以湖南为例[J].林业科学,2008,44(11):64-68.
WANG M Y,SHU L F,WANG Q H,etal.Forest fire occurrence in short term under the impacts of snow damage in south of China,a case study in Hunan Province [J].Scientia Silvae Sinicae,2008,44(11):64-68.(in Chinese)
[10] 储昌超,张贵,孙玉荣.基于克里金方法的湖南森林火灾趋势预测研究[J].中南林业科技大学学报,2014,34(6):66-70.
CHU C C,ZHANG G,SUN Y R.Trend forecast of forest fire in Hunan Province based on Kriging interpolation model [J].Journal of Central South University of Forestry & Technology,2014,34(6):66-70.(in Chinese)
[11] 郭海峰,禹伟.湖南省森林火险天气等级预测模型研究[J].中南林业科技大学学报,2016,36(12):44-47,67.
GUO H F,YU W.Study weather grade prediction model of forest-fire risk in Hunan Province[J].Journal of Central South University of Forestry & Technology,2016,36(12):44-47,67.(in Chinese)
[12] OLIVEIRA S,OEHLER F,SAN-MIGUEL-AYANZ J,etal.Modeling spatial patterns of fire occurrence in Mediterranean Europe using multiple regression and random forest[J].Forest Ecology & Management,2012,275(4):117-129.
[13] 李欣海.随机森林模型在分类与回归分析中的应用[J].应用昆虫学报,2013,50(4):1190-1197.
LI X H.Using “random forest” for classification and regression [J].Entomological Knowledge,2013,50(4):1190-1197.(in Chinese)
[14] 张雷,王琳琳,张旭东,等.随机森林算法基本思想及其在生态学中的应用——以云南松分布模拟为例[J].生态学报,2014,34(3):650-659.
ZHANG L,WANG L L,ZHANG X D,etal.The basic principle of random forest and its applications in ecology:a case study ofPinusyunnanensis[J].Acta Ecologica Sinica,2014,34(3):650-659.(in Chinese)
[15] FABRICIUS K E.Classification and regression trees:a powerful yet simple technique for ecological data analysis[J].Ecology,2000,81(11):3178-3192.
[16] LOUISR I,ANANTHAM P,STEPHENN M,etal.Estimating potential habitat for 134 eastern US tree species under six climate scenarios[J].Forest Ecology & Management,2008,254(3):390-406.
[17] BREIMAN L.Random forest [J].Machine Learning,2001,45:5-32.
[18] 王璟睿,沈文娟,李卫正,等.基于RapidEye的人工林生物量遥感反演模型性能对比[J].西北林学院学报,2015,30(6):196-202.
WANG J R,SHEN W J,LI W Z,etal.Performances comparison of multiple non-linear models for estimating plantations' biomass based on RapidEye imagery [J].Journal of Northwest Forestry University,2015,30(6):196-202.(in Chinese)
[19] CUTLER D R,EDWARDS T C,BEARD K H,etal.Random forests for classification in ecology[J].Ecology,2007,88(11):2783-92.
[20] RODRIGUES M,RIVA J D L.An insight into machine-learning algorithms to model human-caused wildfire occurrence [J].Environmental Modeling & Software,2014,57:192-201.
[21] 张馨月,苏晓慧.四川省林火次数与气象因子的相关性研究[J].西北林学院学报,2017,32(3):176-180.
ZHANG X Y,SU X H.Correlation analysis on forest fire occurring frequency and meteorological factors in Sichuan [J].Journal of Northwest Forestry University,2017,32(3):176-180.(in Chinese)
[22] WOTTON B M.Interpreting and using outputs from the Canadian forest fire danger rating system in research applications [J].Environmental & Ecological Statistics,2009,16(2):107-131.
[23] 郭福涛,苏漳文,马祥庆,等.大兴安岭塔河地区雷击火发生驱动因子综合分析[J].生态学报,2015,35(19):6439-6448.
GUO F T,SU Z W,MA X Q,etal.Climatic and non-climatic factors driving lightning-induced fire in Tahe,Daxing'an mountain[J].Acta Ecologica Sinica,2015,35(19):6439-6448.(in Chinese)
[24] 张恒,金森,邸雪颖.基于FWI湿度码的塔河林业局地表凋落物含水率预测[J].应用生态学报,2014,25(7):2049-2055.
ZHANG H,JIN S,DI X Y.Prediction of litter moisture content in Tahe forestry bureau of northeast China based on FWI moisture codes [J].Chinese Journal of Applied Ecology,2014,25(7):2049-2055.(in Chinese)
[25] 信晓颖,江洪,周国模,等.加拿大森林火险气候指数系统(FWI)的原理及应用[J].浙江农林大学学报,2011,28(2):314-318.
XIN X Y,JIANG H,ZHOU G M,etal.Canadian forest fire weather index (FWI) system:a review [J].Journal of Zhejiang A&F University,2011,28(2):314-318.(in Chinese)
[26] 梁慧玲,林玉蕊,杨光,等.基于气象因子的随机森林算法在塔河地区林火预测中的应用[J].林业科学,2016,52(1):89-98.
LIANG H L,LIN Y R,YANG G,etal.Application of random forest algorithm on the forest fire prediction in Tahe area based on meteorological factors[J].Scientia Silvae Sinicae,2016,52(1):89-98.(in Chinese)
[27] 郭福涛,苏漳文,王光玉,等.我国北方针叶林人为火发生的预测模型[J].应用生态学报,2015,26(7):2099-2106.
GUO F T,SU Z W,WANG G Y,etal.Prediction model of human-caused fire occurrence in the boreal forest of northern China [J].Chinese Journal of Applied Ecology,2015,26(7):2099-2106.(in Chinese)
[28] CHANG Y,ZHU Z,BU R,etal.Predicting fire occurrence patterns with logistic regression in Heilongjiang Province,China [J].Landscape Ecology,2013,28(10):1989-2004.
[29] 孙瑜,史明昌,彭欢,等.基于MAXENT模型的黑龙江大兴安岭森林雷击火火险预测[J].应用生态学报,2014,25(4):1100-1106.
SUN Y,SHI M C,PENG H,etal.Forest lighting fire forecasting for Daxing'anling mountains based on MAXENT model [J].Chinese Journal of Applied Ecology,2014,25(4):1100-1106.(in Chinese)
[30] 尹华,胡玉平.基于随机森林的不平衡特征选择算法[J].中山大学学报:自然科学版,2014,53(5):59-65.
YIN H,HU Y P.An imbalanced feature selection algorithm based on random forest [J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2014,53(5):59-65.(in Chinese)
[31] 巩亚楠,帕提麦·马秉成,朱登浩,等.随机森林与Logistic回归在预约挂号失约影响因素预测中的应用[J].现代预防医学,2014,41(5):769-772.
GONG Y N,PA T M,ZHU D H,etal.Application of random forests and logistic regression in prediction of influencing factors of missed appointment registration [J].Modern Preventive Medicine,2014,41(5):769-772.(in Chinese)
[32] 彭国兰.随机森林在企业信用评估中的应用[D].厦门:厦门大学,2007.
[33] LIAW A,WIENER M.Classification and regression by random forest [J].R.News,2002,23:23.
[34] 吕杰,汪康宁,李崇贵,等.基于小波变换和随机森林的森林类型分类研究[J].西北林学院学报,2016,31(6):264-267.
LYU J,WANG K N,LI C G,etal.Classification of forest types based on discrete wavelet transform and random forests from GF-1 images[J].Journal of Northwest Forestry University,2016,31(6):264-267.(in Chinese)
[35] GENUER R,POGGI J M,TULEAU-MALOT C.Variable selection using random forests [M].New York:Elsevier Science Inc.,2010.
[36] 武晓岩,闫晓光,李康.基因表达数据的随机森林逐步判别分析方法[J].中国卫生统计,2007,24(2):151-154.
WU X Y,YAN X G,LI K.The stepwise discriminant analysis of random forests used in gene expression data[J].Chinese Journal of Health Statistics,2007,24(2):151-154.(in Chinese)
[37] LITTELL J S,MCKENZIE D,PETERSON D L,etal.Climate and wildfire area burned in western USA ecoprovinces,1916-2003[J].Ecological Applications,2009,19(4):1003-1021.
[38] WOTTON B M,MARTELL D L,LOGAN K A.Climate change and People-caused forest fire occurrence in Ontario [J].Climatic Change,2003,60(3):275-295.
[39] FLANNIGAN M D,STOCKS B J,WOTTON B M.Forest fires and climate change [J].Science of the Total Environment,262:221-230.
[40] 郭福涛,苏漳文,马祥庆,等.大兴安岭塔河地区雷击火发生驱动因子综合分析[J].生态学报,2015,35(19):6439-6448.
GUO F T,SU Z W,MA Q X,etal.Climatic and non-climatic factors driving lightning-induced fire in Tahe,Daxing′an mountain[J].Acta Ecologica Sinica,2015,35(19):6439-6448.(in Chinese)
[41] CHANG Y,ZHU Z,BU R,etal.Predicting fire occurrence patterns with logistic regression in Heilongjiang Province,China [J].Landscape Ecology,2013,28(10):1989-2004.
[42] 田晓瑞,MCRAE D J,舒立福,等.大兴安岭地区森林火险变化及FWI适用性评估[J].林业科学,2010,46(5):127-132.
TIAN X R,Douglas J M,SHU L F,etal.Changes of forest fire danger and the evaluation of the FWI system application in the Daxing'anling region[J].Scientia Silvae Sinicae,2010,46(5):127-132.(in Chinese)
[43] PAUSAS J G.Changes in fire and climate in the eastern iberian peninsula (mediterranean basin) [J].Climatic Change,2004,63(3):337-350.
[44] GUO F,SU Z,WANG G,etal.Wildfire ignition in the forests of southeast China:identifying drivers and spatial distribution to predict wildfire likelihood [J].Applied Geography,2016,66:12-21.
[45] STOCKS B J.Forest fires and sustainability in the boreal forests of Canada [J].Ambio,1998,27(7):545-550.
[46] RODRIGUES M,RIVA J D L,FOTHERINGHAM S.Modeling the spatial variation of the explanatory factors of human-caused wildfires in Spain using geographically weighted logistic regression [J].Applied Geography,2014,48(48):52-63.
[47] SAEFUDDIN A,SETIABUDI N A,FITRIANTO A.On comparison between logistic regression and geographically weighted logistic regression:with application to indonesian poverty data[J].World Applied Sciences Journal,2012,19(2):205-210.
[48] 赵玉,王红,张珍珍.基于遥感光谱和空间变量随机森林的黄河三角洲刺槐林健康等级分类[J].遥感技术与应用,2016,31(2):359-367.
ZHAO Y,WANG H,ZHANG Z Z.Forest healthy classification of robinia pseudoacacia in the Yellow River Delta,China based on spectral and spatial remote sensing variables using random forest[J].Remote Sensing Technology and Application,2016,31(2):359-367.(in Chinese)
[49] 赵铜铁钢,杨大文,蔡喜明,等.基于随机森林模型的长江上游枯水期径流预报研究[J].水力发电学报,2012,31(3):18-24,38.
ZHAO T T G,YANG D W,CAI X M,etal.Predict seasonal low flows in the upper Yangtze River using random forests model [J].Journal of Hydroelectric Engineering,2012,31(3):18-24,38.(in Chinese)
[50] 赖成光,陈晓宏,赵仕威,等.基于随机森林的洪灾风险评价模型及其应用[J].水利学报,2015,46(1):58-66.
LAI C G,CHEN X H,ZHAO S W,etal.A flood risk assessment model based on random forest and its application[J].Journal of Hydraluic Engineering,2015,46(1):58-66.(in Chinese)
