关于“”的跨国讨论*

□刘 莹 郜舒竹

（首都师范大学初等教育学院，北京 100037）

关于跨国讨论的话题，其实是关于算术运算规律对于有理数指数幂运算的继承性问题“.继承性”这一说法始见于19世纪英国数学家乔治·皮克科（George Peacock，1791－1858）于1830年在剑桥大学出版社出版的《论代数》（ATreatise on Algebra）前言中，其本意是研究算术中的形式如何继承到代数系统中，也就是如何保持算术运算规律和法则适用于代数运算的问题[1].这一说法后来被广泛应用于数学不同领域的类似研究中.

《普通高中数学课程标准（2017年版）》将有理数指数幂以及实数指数幂安排在“指数函数”课程内容中，具体要求是“了解指数的拓展过程……”[2].指数的拓展过程，经历从自然数开始，增加0和负整数到整数；进一步增加分数到有理数；而后增加无理数到实数等.在这样的过程中，自然会不断出现继承性的问题.

一、问题的缘起

1995年7月，两位以色列学者在荷兰出版的、数学教育领域久负盛名的期刊《数学中的教育研究》（Educational Studies in Mathemat⁃ics）上发表一篇研究以色列高中数学教师本体性知识的文章[3].其中有一个如何看待分数指数幂的测试题.调查结果显示，大部分被试教师都认为表达式的含义是唯一确定，其确定的结果为.而文章作者认为这样的回答是不完善的，理由是如果运用不同的方法进行化简，会出现两个不同的结果.

方法1：

方法2

这样就出现形如“”的悖论.作者认为像这样出现多种结果的表达式，等同于不能确定其结果，因此是不能定义的，就像零作为分母的表达式无法定义一样.作者认为高中数学教师的本体性知识应当具有这样的解释性特征，能够认识到表达式的不确定性.

一年后的1996年9月，两位美国学者在同一期刊上撰文表达了不同观点[4].悖论出现的原因，是前面方法2中出现形如“的推理.悖论的出现并不是因为的意义不确定，而是与不具备相等关系.为了避免“”这样的推理，只需要在有理数指数幂的定义中，对分数指数增加“分子与分母互质”，或“最简分数（即约分数）”即可.作者列举了在美国出版的两个版本的大学代数教科书作为例证.

第一本书中对分数指数幂的定义为：如果a是任意一个实数，并且n是使得a的n次根存在的正整数，那么规定.进一步，如果m是一个正整数，并且与n互质，那么规定在这个定义中，由于有“m与n互质”的要求就不能写为，也就避免了的情况，那么表达式就有唯一确定的结果-2.

作者列举的第二本书中对ar的定义为：a是任意实数，如果r是一个有理数，并且a的q次根是一个实数，那么规定ar=ar1.其中r1是r的最简分数形式.这个定义与前面类似，同样限制了与的相等关系，因此化简后的结果只能等于-2.文章结论认为的存在是合理的，只要对有理数指数幂给出恰当的定义，就可以使得底数为负数的分数指数幂表达式的含义唯一确定.

综上，如何理解的问题，实质是如何看待与的关系问题.在小学数学中就已经熟悉的分数基本性质，能否直接推理出与的相等关系？

二、函数的视角

与的关系，可以通过三个幂函数以及之间的关系进行解释.在实数范围内，是一个定义域为(-∞,+∞)的奇函数.-8在其定义域内，因此从函数的视角看，实数范围内是有确定意义的，其函数值唯一确定，等于-2（见图1）.

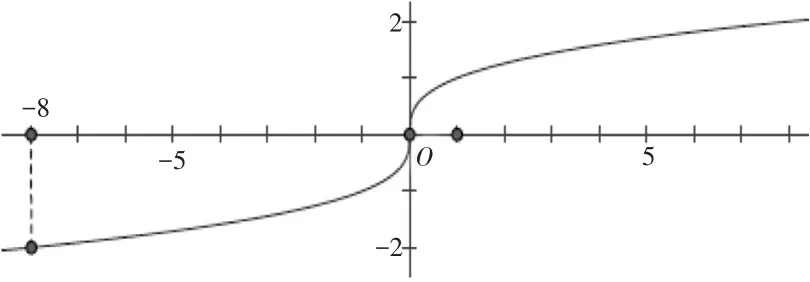
图1

函数是实数范围内定义域为(-∞,+∞)的偶函数.因此对于x=-8时也是有意义的，此时的函数值为2，而不是-2（见图2）.

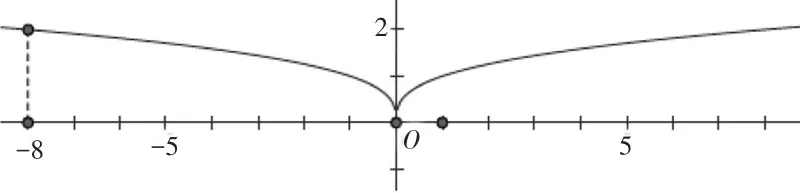
图2

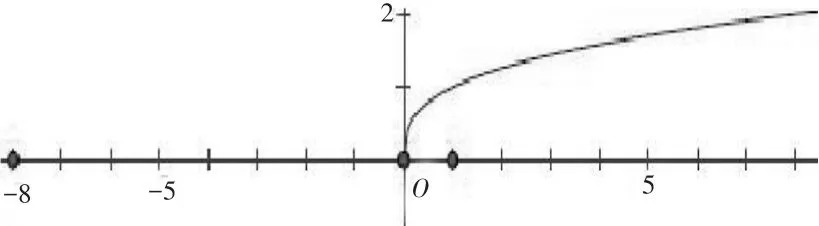
图3

由此看出，三个幂函数以及互不相同.因此算术中所熟知的运算规律并不能直接继承于有理数指数幂的运算.比如使用乘法交换律将变为或，每一次的改变都导致函数定义域以及相关性质发生变化.

因此对于与的不同就可以理解了，并不是无法定义，而是继承性地使用算术运算规律，从变为，使得的含义发生了改变，进而出现形如的悖论.

事实上，算术中所熟悉的运算规律通常都是在正整数范围内使用的，这些规律一般可以继承到底数为正数时的有理数和实数指数幂运算.这也就是对于指数函数y=ax为什么需要规定底数a＞0的道理.

三、复数的眼光

10年后的2005年11月，两名韩国学者在加拿大出版的期刊《为了数学学习》（For the Learning of Mathematics）上撰文，对与的关系做了进一步讨论[5].基本观点是把表达式和分别看作是方程x3=-8和x6=（-8）2在复数范围内解的集合.

按照代数基本定理，方程x3+8=0在复数范围内有三个解，也就是说可以把表达式理解为是含有三个元素的集合.应用熟知的欧拉公式：eix=cosx+isinx，可以求出这三个元素：

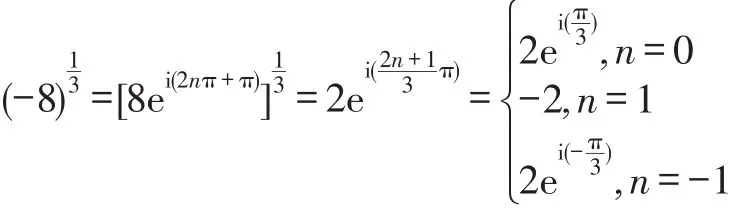
这三个解在复平面上分别对应三个不同的点，其极坐标形式分别为：（见图4）.

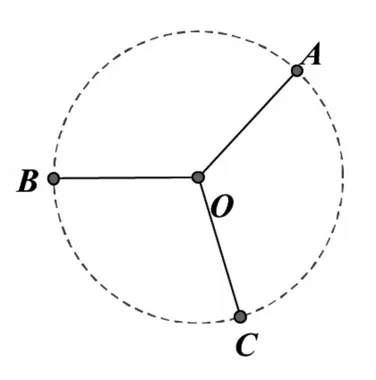
图4

按照这样的理解，表达式是有确定意义的，其存在自然也是合理的.可以定义为含有三个元素的集合：

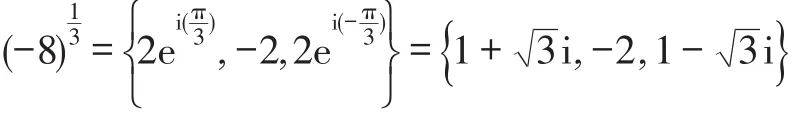
同样，方程x6=（-8）2在复数域有六个解，分别对应复平面上六个不同的点：（见图5）.

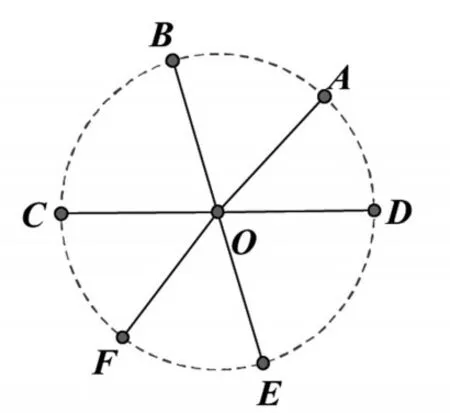
图5

因此表达式所表示的集合为：

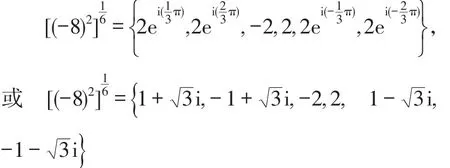
这说明在复数范围内，表达式和都是有确定意义的，但二者是不同的.分别表示两个不同的集合，而且前者是后者的真子集.二者之间的关系不应当用等号“=”表达，而应当用集合间的关系符号表达为：

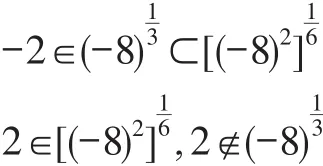
至此，应当说表达式是有确定意义的，并且是可以定义的.在实数范围内表达一个唯一确定的数-2，而在复数范围内表达一个包含三个元素的数集.另外，对于底数小于0的指数幂，算术中所熟悉的诸如交换率、结合律、分配率等运算规律，不能直接继承性地使用.因此与并不具有相等关系，运用乘法交换率由推演出来的两个表达式和，其含义也是不一样的.

以上对与关系的讨论，反映出从算术到代数拓展过程中，人的认知规律与数学逻辑规律不一致的现象.从认知的角度说，期望将算术中已经熟悉的自然数的运算规律，自然而然地运用到有理数指数上，使得与具有相等关系.当这种期望违背了数学推理中的逻辑规律时，数学家就需要研究如何才能使得这样的继承性得以保持.

数学课程与教学面临类似的问题，学生的数学学习是循序渐进、螺旋上升的过程，之前已经熟悉的知识和经验，在新的范围内能否继承？为什么能够或者不能够继承？怎样才能继承？诸如此类的继承性问题其实是学生学习数学过程中的难点，同时也是深入理解新知识的重点.应当在数学课程与教学研究中引起足够的重视 .

［1］PEACOCK G.A treatise on algebra(VOL.Ⅰ)［M］.London:Cambridge University Press,1830:IV.

［2］中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2018：17.

［3］EVEN R,TIROSH D.Subject-matter knowledge and knowledge about students as sources of teacher-presentations of the subjectmatter［J］.Educational Studies in Mathematics,1995,29(1):1-20.

［4］GOEL S K,ROBILLARD M S.The equation:=2［J］.Educational Studies in Mathematics,1996,33(3):319-320.

［5］CHOI Y,DO J.Equality involved in 0.999...and［J］.For the Learning of Mathematics,2005,25(3):13-15,36.